轨道车辆车体半主动式磁流变吸振器的减振特性研究
周伟浩, 文永蓬, 尚慧琳, 宗志祥, 郭林生
(1. 上海工程技术大学 城市轨道交通学院,上海 201620; 2. 上海应用技术大学 机械工程学院,上海 201418)
城市轨道交通车辆运行时,轨道不平顺产生的轮轨振动经过一系和二系悬挂系统衰减传递至车体,对旅客乘坐舒适度造成一定影响。动力吸振器由于具有结构简单、减振效果好的优点,已成为降低车体振动、提高旅客乘坐舒适度的有效手段之一[1]。
近年来,国内外学者对动力吸振器已进行大量研究。Foo等[2]在车体中部布置了动力吸振器,一定程度上改善了乘客舒适度;Tomioka等[3]将转向架之间的纵向运动作为动力吸振器,明显降低了车体的弯曲振动;周劲松等[4-8]引入了车辆运行平稳性指标对车体动力吸振器的减振效果进行评价,并利用最优频率比和最优阻尼比对车体动力吸振器进行优化,大大降低了对车体垂向一阶频率的要求;文永蓬等[9]考虑轨道对车体耦合振动的影响,研究出适用于轨道车辆动力吸振器的设计优化方法,并提出了一种考虑车速变化以及速度区间运行概率的DVA减振评价指标,对动力吸振器的减振性能进行定量计算,但这种设计方法是针对被动式动力吸振器,所谓被动式动力吸振器,即设计好之后吸振器参数不能调节、吸振器固有频率不变,因此动力吸振器减振频段较窄,减振效果受到限制。刘耀宗等[10]设置多个固有频率不同的吸振器对不同振动频率点进行吸振,拓宽了吸振器的工作频段,但是对于每个吸振器而言,依然属于被动式,这种固频混合式被动式吸振器,一般只针对振动系统的有限个频率,这就大大限制了动力吸振器的应用范围。与被动式吸振器不同,主动式吸振器的工作原理是利用外部能源使吸振器在车辆振动瞬时施加控制力,以迅速衰减车辆振动。胡杰等[11]将永磁铁作为吸振器安装在被控结构上,通过电磁铁给永磁铁一个作用力来实现对结构振动的控制,作用力的大小通过调节电流的大小来实现,这种主动式吸振器能够实现宽频减振,但是结构复杂、控制精度要求高、耗能大、稳定性差且价格昂贵等缺点给主动式吸振器的设计和应用带来了困难。半主动式吸振器(又称自适应式吸振器)通过较低的能耗动态改变吸振器的刚度等参数,从而使有效吸振频率与减振对象的外干扰力频率满足协调关系,不仅拓宽了吸振器的减振频段,而且吸振效果接近主动式的吸振效果,并且,与主动式吸振器相比具有所需的控制能量小、易于实现等特点。Yong等[12]通过控制压电叠堆的变形改变两个弹簧的耦合程度来改变刚度,实现吸振器的移频;除了机械调频和电磁调频外,智能材料也常常用于吸振器的半主动控制。磁流变弹性体的弹性模量可受磁场强度控制,且控制具有响应快、可逆、稳定等优点,满足自适应吸振器的设计需要。Shiga等[13]利用磁流变效应,将硅树脂和铁粉混合制备出具有磁控性能的材料,其刚度可根据周围磁场强度的大小发生变化,为磁流变弹性体的研究奠定了基础;Holdhuse等[14]设计了一种拉压式的磁流变吸振器,以磁流变弹性材料作为吸振器的弹簧单元,实现了吸振器的宽频工作;Deng等[15-18]对磁流变吸振器进行了系统的研究和总结,制备了具有国际领先水平的硅橡胶基和天然橡胶基磁流变弹性体,建立了一整套评价磁流变弹性体静态力学性能、动态力学性能和机械性能的测试系统,并发展了一系列磁流变弹性体移频式自适应吸振器。综上,被动式吸振器减振效果受到限制,而主动式吸振器技术要求过高难以被实现与应用,考虑到城市轨道车辆-轨道一体系统是一个工况复杂的耦合振动系统,钢轨和车辆振动耦合,车速、载客量的变化频繁,这些因素会引起轨道车辆车体振动频率发生改变,对宽频减振技术有一定需求,特别是亟需轨道车体半主动式动力吸振器的设计和优化方法。
为此,论文利用赫兹线性接触理论建立将半主动式磁流变吸振器安装在车体下方的车轨耦合模型;考虑车辆运行中不同工况对车体振动频率的影响,并基于课题组前期研究的被动式动力吸振器的设计方法和磁流变弹性体的动态特性,研究车轨耦合振动系统中的磁流变吸振器的设计方法,针对载客量及车速变化对车体振动的影响采用多元回归分析法拟合最佳设计频率表达式,并对刚度进行优化,进而分析磁流变吸振器对车体垂向振动特性的影响以及相较于被动式动力吸振器的优点;最后根据Sperling指标对轨道车体磁流变吸振器的减振效果进行验证,证明论文针对磁流变吸振器的设计方法的有效性。
1 包含磁流变弹性体的半主动吸振器的车轨垂向振动模型
如图1为包含磁流变弹性体的半主动吸振器的车轨垂向振动模型(以下简称磁流变吸振器),磁流变吸振器安装在车体下方中部。图中,车体、转向架、轮对均被看作为刚体。振动过程中,车辆中的八个部件共包含11个自由度:车体浮沉和点头运动、即一个线位移Zc和一个角位移φc, 前后转向架的浮沉和点头运动、 即两个线位移Zt1、Zt2和两个角位移φt1、φt2, 车轮的浮沉运动、即四个线位移ZW1、ZW2、ZW3、ZW4,磁流变吸振器的浮沉运动、即一个线位移Zd。 车辆下方依次为钢轨、浮置板和路基。轨下垫片和支撑弹簧分别作为钢轨和浮置板、浮置板和路基之间的弹性连接装置。Zr、Zs分别为钢轨和轨道浮置板因浮沉运动产生的线位移。其余参数如表1所示。
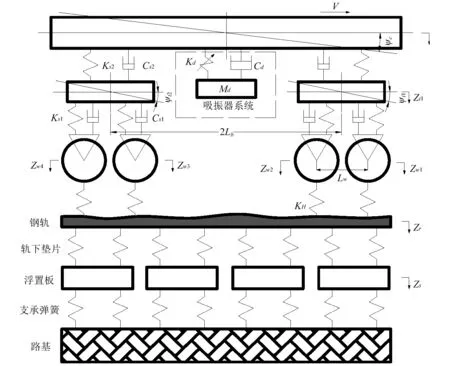
图1 磁流变吸振器的车轨垂向振动模型Fig.1 The vertical vehicle-track vibration modelwith MRE absorber
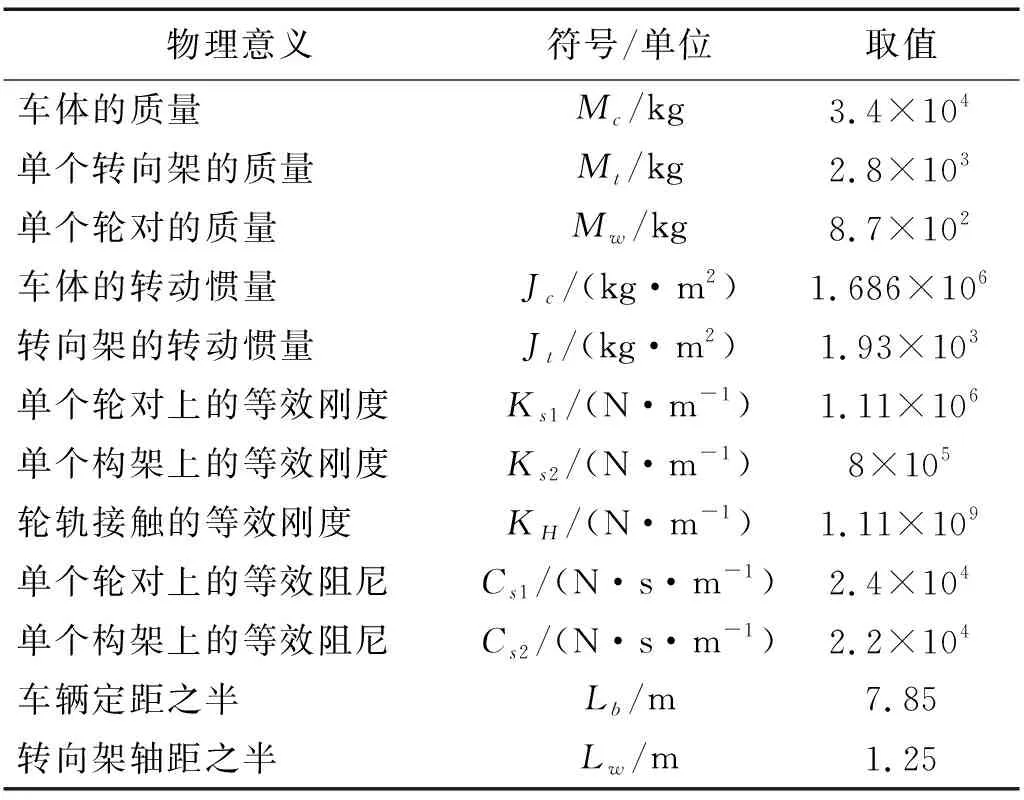
物理意义符号/单位取值车体的质量Mc/kg3.4×104单个转向架的质量Mt/kg2.8×103单个轮对的质量Mw/kg8.7×102车体的转动惯量Jc/(kg·m2)1.686×106转向架的转动惯量Jt/(kg·m2)1.93×103单个轮对上的等效刚度Ks1/(N·m-1)1.11×106单个构架上的等效刚度Ks2/(N·m-1)8×105轮轨接触的等效刚度KH/(N·m-1)1.11×109单个轮对上的等效阻尼Cs1/(N·s·m-1)2.4×104单个构架上的等效阻尼Cs2/(N·s·m-1)2.2×104车辆定距之半Lb/m7.85转向架轴距之半Lw/m1.25
2 模型的求解
2.1 轮轨接触力的求解
轮轨接触时由于轨道不平顺而产生耦合振动,车轮产生垂向位移ZW、钢轨产生垂向位移Zr。为便于计算,工程上往往将非线性的轮轨接触力线性化,轮轨赫兹接触理论公式[19-20]为
Fi=KH(ZWi-Zri-qi)
(1)
式中:i=1,2,3,4,Fi为第i轴轮轨相互作用力,KH为轮轨接触刚度,ZWi为第i轴车轮的垂向位移,Zri为第i轴轮轨接触处钢轨的垂向位移,qi为第i轴处轨道不平顺度。
将式(1)进行傅里叶变换
Fi(ω)=KH(ZWi(ω)-Zri(ω)-qi(ω))
(2)
根据位移和力之间的关系,有
(3)
由式(2)、(3)整理可得
(4)
式中:αW、αR、αC分别为车轮柔度,钢轨柔度,轮轨接触柔度。鉴于篇幅限制,以上各柔度的表达式不一一列举。
2.2 车辆振动响应特性求解
据拉格朗日方程,获得利用磁流变弹性体的动力吸振器的11自由度车辆垂向动力学表达式,并进行傅里叶变换
(-ω2[M]+jω[C]+[K])Z(ω)={F(ω)}
(5)
式中: j为虚数单位,Z(ω)为位移矩阵的傅里叶变换, [M]为车辆各部件质量矩阵, [C]为系统阻尼矩阵, [K]为受磁流变弹性体刚度Kd影响的系统刚度矩阵,矩阵如下:
论文采用定点激励模型[21],即车轮不动,轨道不平顺以一定速度向后运动,所以各车轮下的振动激励都为q1。 对式(5)进行变换, 令[H(ω)]为车辆振动系统的频率响应特性矩阵,并以轨道不平顺激励q1为输入、 各质量位移Zi为输出,有
[H(ω)]=q1(ω)-1{Z(ω)}=q1(ω)-1×
(-ω2[M]+jω[C]+[K])-1{F(ω)}=
[h1(ω) …hi(ω) …h11(ω)]T
(6)
式中:hi(ω)为车辆系统各部件的垂向振动频率响应特性,i=1,2,…,11, 其中h1(ω)为车体响应特性,h11(ω)为磁流变吸振器响应特性。
(7)
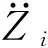
(8)
式中:Gq1(ω)为轨道不平顺激励q1(ω)的加速度功率谱密度。
3 磁流变吸振器的设计方法
为实现对车体的宽频减振,将刚度可变、阻尼比不可变的磁流变弹性体材料作为动力吸振器的弹性、阻尼混合元件,将车辆车体视作主振系,通过共振原理吸收主振系振动能量,简化后的二自由度“主振系-磁流变吸振器”振动模型如图2所示。图2中,Mj为主振系的质量,Kj、Cj为对城轨车辆中复杂的刚度系统和阻尼系统化简后的等效值,Kd、Cd为磁流变吸振器的刚度和阻尼。

图2 “主振系-磁流变吸振器”振动模型Fig.2 Vibration model of the main system and MREdynamic vibration absorber
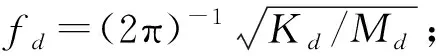
在二自由度振动模型中,当吸振器与主振系的频率比满足最优同调条件[22]即γ=(1+μ)-1时, 吸振器才能最大程度吸收主振系的振动能量,则吸振器的固有频率fd应设计为
(9)
由此可知吸振器的刚度设计值Kd为
(10)
由于磁流变弹性体材料的阻尼比ζd为定值, 根据吸振器的阻尼比公式可知吸振器的阻尼Cd为
Cd=4πMdfdζd
(11)
由式(11)可知,为实现宽频减振,吸振器的刚度值需根据主振系的振动频率的改变而改变。刚度的变化由磁流变弹性体实现,当磁流变弹性体受到磁场作用时,弹性体中的铁磁颗粒磁化后产生相互作用力,使其剪切模量G可根据磁场强度B的改变而改变, 而剪切模量与刚度Kd呈线性关系
Kd=(A·H-1)G(B)
(12)
式中:A为磁场剪切面积,H为磁流变弹性体的厚度。
根据式(12)可知,磁流变弹性体的刚度大小可通过磁场强度B进行控制,通过实时监测车体振动频率,即轨道不平顺对车辆的振动激励频率,再根据式(10)调整吸振器中磁流变弹性体的刚度,使吸振器的固有频率与车体振动频率时刻满足最优同调条件,从而在有效频率范围内实现宽频减振。根据式(10)、式(12)可知吸振器固有频率fd与磁场强度B的关系为
(13)
论文选用的磁流变弹性体样品[23]的弹性模量G与磁感应强度B之间的关系,如图3所示。
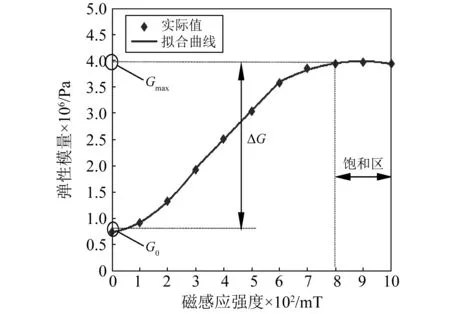
图3 弹性模量G与磁感应强度B的关系图Fig.3 Relation between elastic modulus G andmagnetic intensity B
由图3可知,该种磁流变弹性体材料在未受磁场影响的情况下, 剪切模量模量G0=0.74 MPa,当磁场饱和(Bm≈800 mT),即随着磁场强度增加、磁流变弹性体材料的剪切模量不再增加时,磁致剪切模量ΔG=3.23 MPa, 最大剪切模量Gmax=3.97 MPa。
由于最大剪切模量和最小剪切模型的存在,剪切模量变化范围一定,磁流变吸振器功能将受到一定限制,只能在车体振动全频段中的某一段进行车体振动抑制,因此该频段即为磁流变吸振器可正常工作的有效频段,即fwork。当车体振动超过有效工作频段fwork时, 磁流变吸振器可能会失效。有效工作频段fwork的选择, 需要先对磁流变吸振器的有效移频率ηd进行计算, 再结合车体实际振动特性确定,根据式(13)可知
(14)
城市轨道车辆不仅结构复杂,而且工况变化频繁,其中载客量A的变化会改变车体振动频段的宽度,车速V的变化会改变车体振动峰值频率的大小和个数。因此,仅利用最优同调条件得到的吸振器固有频率并不能使磁流变吸振器发挥很好的减振作用,需要根据仿真实验捕捉不同工况、不同车体振动频率下的吸振器最佳设计频率fdesign,即此时车体振动加速度谱最小, 并代入式(10)对吸振器刚度Kd进行优化。
综上,轨道车辆磁流变吸振器参数设计的一般步骤为:
(1) 根据轨道车辆的实际情况和安全性等因素的考虑,确定磁流变吸振器和主振系的质量比μ;
(2) 根据磁流变吸振器的有效移频率ηd和车体实际振动频段,确定吸振器的有效工作频段fwork;
(3) 确定不同工况、不同工作频率下的吸振器最佳设计频率fdesign, 并拟合磁流变吸振器的设计频率表达式fdesign(A,V,fwork), 从而,确定磁流变吸振器的设计刚度Kd, 提升目标频率fj处的减振能力。
以上步骤流程如图4所示,确定质量比μ和有效工作频段fwork是必要条件,确定这两个参数是进行磁流变吸振器设计的必由之路。接着针对不同工况下的车体振动目标频率fj寻找吸振器最佳设计频率fdesign, 由于不同的吸振器固有频率对车体的减振效果不同,通过遍历吸振器固有频率fd, 当车体振动加速度谱最小时即认为此时吸振器的减振效果最佳, 则以此时的吸振器固有频率fd作为吸振器的最佳设计频率fdesign, 这是磁流变吸振器设计的关键步骤。依据上述步骤中获得的载重、车速以及有效工作频段以及相应的最佳设计频率,可以拟合出设计频率表达式fdesign(A,V,fwork), 并由此对吸振器刚度Kd进行优化,从而实现较好的减振效果。
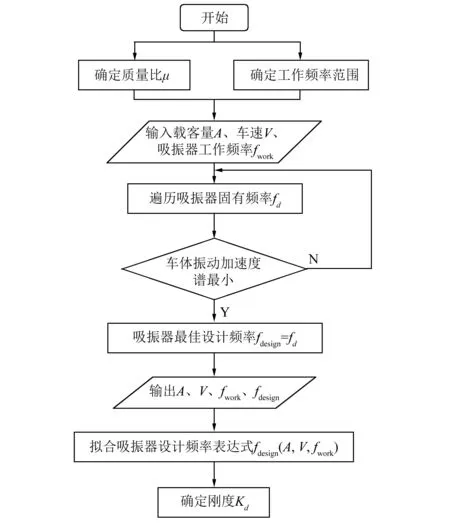
图4 轨道车辆磁流变吸振器参数设计流程图Fig.4 Flow chart of parameters design of MREabsorber for railway vehicle
4 磁流变吸振器参数的确定
4.1 确定质量比
根据文献[9]可知,随着质量比μ的增加,吸振器所能吸收的能量越大,即对车体的减振效果越好,但是,考虑到吸振器对车辆限界的影响、经济性以及布置的难易程度,下面的研究中,均取μ=0.1。
4.2 确定有效工作频段
根据图3和式(14)计算,此磁流变弹性体材料为核心的吸振器,其有效工作频段fwork的有效移频率为130%。
图5是车辆在空载AW0和超载AW3两种情况下,车速分别为40 km/h、50 km/h、60 km/h、70 km/h、80 km/h时的车体垂向振动加速度谱。在图5(a) 中,不同载客量、不同车速下的车体振动峰值频率主要均集中在1 Hz到2.3 Hz之间。在图5(b)中,车体振动峰值频率向低频段略微偏移,但也集中在1 Hz~2.3 Hz之间。因而,可以认为轨道车辆车体实际振动频段在此区间。
根据磁流变体材料获得的有效移频率,可知
fwork=f0×(1~2.3)
(15)
式中:f0为磁流变吸振器工作的初始频率。
由于1~2.3 Hz可基本囊括各工况下车体的振动峰值频率,因此磁流变吸振器工作的初始频率f0可确定为1 Hz,则磁流变吸振器的有效工作频段fwork为1~2.3 Hz。在有效工作频段内,磁流变吸振器可以实现对车体的宽频减振,但是当车体振动频率超过磁流变弹性体材料的有效工作频率范围时,磁流变吸振器则退化为传统被动式吸振器。当车体振动频率大于2.3 Hz时,应将磁场强度调节至800 mT,使吸振器固有频率处于最大值,利用吸振器中的阻尼元件可适当展宽减振频段,实现吸振器减振效果最大化;当车体振动频率小于1 Hz时,应撤去磁场使吸振器固有频率处于最小值,减振原理与上述相同。

图5 速度变化对空载、超载下轨道车辆车体垂向振动的影响Fig.5 Effect of speed change on vertical vibration of railwayvehicle body under no-load and overload
4.3 确定最佳设计频率及刚度修正
传统被动式吸振器一般依靠固定点理论对吸振器进行设计,所以利用最优同调条件得到的固有频率fd设计公式(9)、以及文献[9]中针对性很强的被动式吸振器频率修正公式并不完全适用于半主动式磁流变吸振器。不同载客量、不同车速和不同车体振动频率对应的磁流变吸振器的最佳设计频率值fdesign不同,最佳的吸振器设计频率值可使此时的车体振动加速度功率谱密度达到最小,即减振性能最好,因此,为了提高减振性能,有必要在传统被动式吸振器理论及最优同调条件的基础上确定半主动式磁流变吸振器的最佳设计频率,并得到可以使磁流变吸振器与车体很好谐振的磁流变吸振器固有频率计算公式。
由于影响车体垂向振动的各参数具有连续性,需将各参数进行平分量化以便进行后续的数据处理。 将车辆载客重量区间空载至满载工况即AW0~AW3(0~24.96 t)划分为20等份,分别为A1、A2…A20; 运行速度区间0~80 km/h划分为20等份, 分别为V1、V2…V20; 车体垂向振动频段1~2.3 Hz、 即吸振器的工作频段划分为20等份, 分别为fwork1、fwork2…fwork20, 因此, 共有8 000种车体振动情况。分别求解不同载客量、不同车速和不同工作频率对应的磁流变吸振器的最佳设计频率值。
取这8 000种车体振动情况中的某一种进行算例分析。例如,当载客量为A20=24.96 t、车速V20=80 km/h、 吸振器工作频率fwork20=2.3 Hz时,为获得磁流变吸振器的设计频率值fdesign, 遍历吸振器的固有频率fd, 求出不同固有频率下的车体振动加速度谱密度。根据多次仿真实验可知:当吸振器的工作频段fwork为1~2.3 Hz时, 吸振器的设计频率值fdesign不会超过0~10 Hz这一区间, 因此为减少计算量以0~10 Hz为固有频率fd的遍历区间, 结果如图6所示。 在图6中, 当磁流变吸振器的固有频率fd=2.71 Hz时, 车体垂向振动加速度谱密度达到最小值, 即此时的吸振器减振性能达到最佳状态, 那么, 此工况下最佳设计频率fdesign为2.71 Hz。
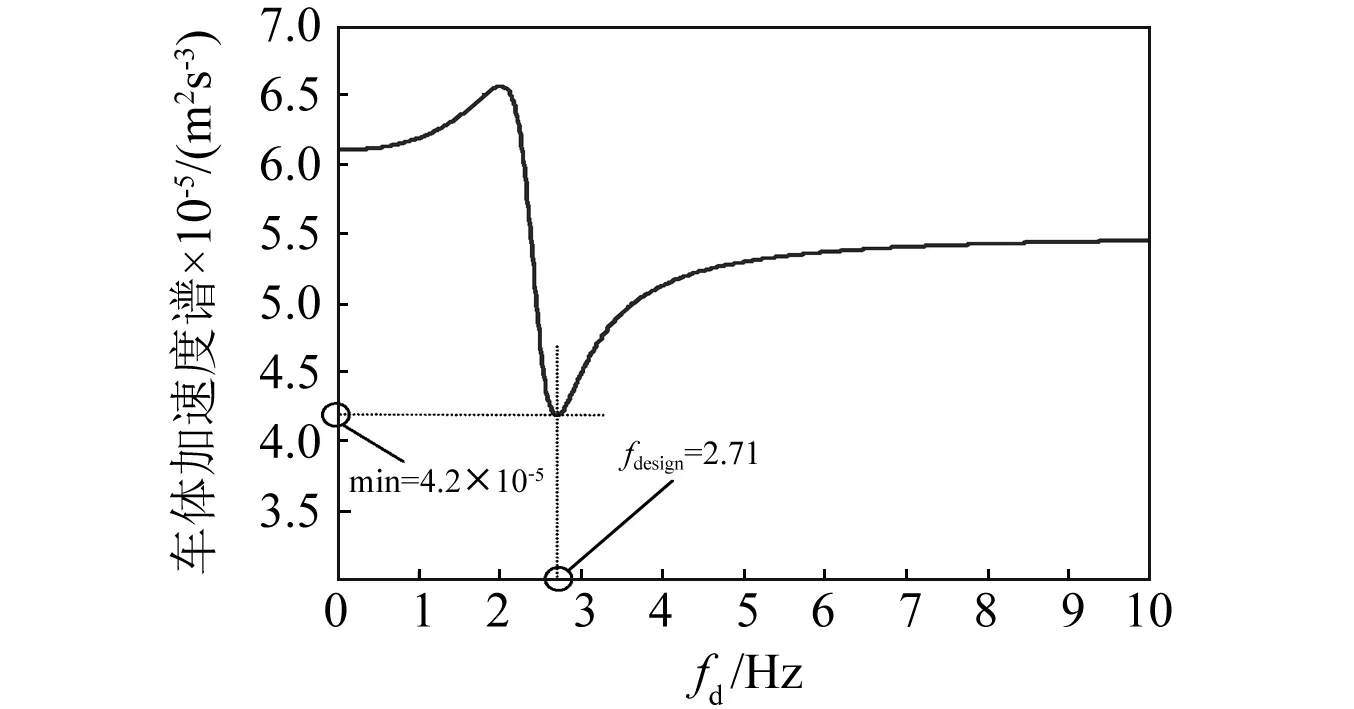
图6 吸振器固有频率对轨道车辆车体垂向振动的影响Fig.6 Effect of vibration absorber’s natural frequency onvertical vibration of railway vehicle body
采用类似的方法,可列出所有计算结果,如表2所示。

表2 不同因素影响下的最佳设计频率值
回归分析法可以在掌握大量观察数据的基础上,利用数理统计方法确定因变量与自变量之间的回归关系,建立函数表达式,并加以外推,还可以估计所建立表达式的精确度。利用回归分析法构造以载客量、车速、吸振器工作频率为自变量、最佳设计频率值为因变量的吸振器设计频率表达式,即fdesign(A,V,fwork)。由于各自变量和因变量之间既存在线性关系,也存在非线性关系,因此采用添加自变量的平方项与交叉乘积项的方法,将多元非线性回归分析模型转变为多元线性回归分析模型进行求解,建模如下:
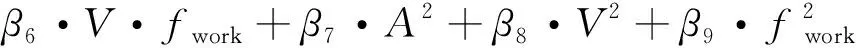
(16)
对模型求解,结果如表3所示。

表3 回归分析结果
拟合优度检验:R2=0.999 8,所以在最佳频率设计值的总变差中,被估计的吸振器设计频率表达式所解释比例是99.98%,拟合程度很高;
方程显著性检验:P1=0, 所以拒绝原假设H0:β1=β2=…=β9=0, 说明回归方程显著,即方程中九个参考变量联合起来确实对最佳频率设计值有显著影响;
自变量显著性检验:当自变量包含车速V时,该项的弃真概率都为1,检验不合格,也就是说车速对最佳频率设计值影响很小,而当自变量包含工作频率fwork时,该项的弃真概率基本为0, 说明工作频率对最佳频率设计值影响显著。 由此可知, 工作频率fwork对最佳频率设计值影响最大,载客量A次之,车速V最小。
因此,磁流变吸振器的最佳设计频率表达式为
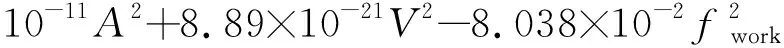
(17)
综上,根据式(10)和式(17)可知,轨道车辆车体磁流变吸振器的最佳刚度设计表达式为
(18)
5 磁流变吸振器的减振效果分析
当车辆运行速度为60 km/h时,车体出现两个振动峰值、振动频段较宽,采用磁流变吸振器的最佳刚度设计表达式对刚度进行优化,并分析磁流变吸振器对车体宽频减振的效果。
图7为车辆运行速度为60 km/h时,安装磁流变吸振器、被动式吸振器和未安装吸振器时车体的垂向振动加速度谱。此时车体出现两个振动峰值频率1.38 Hz、1.94 Hz,采用被动式吸振器在进行车体减振设计时,不得不需要针对两处峰值频率分别设计,分别称为设计Ⅰ、设计Ⅱ。
由图7可知,在磁流变吸振器的工作频段内(1~2.3 Hz),磁流变吸振器的车体垂向振动加速度谱密度都小于被动式吸振器Ⅰ、Ⅱ,减振效果较好;在磁流变吸振器的工作频段外,磁流变吸振器也能发挥良好的减振作用,这是因为此时磁流变吸振器的固有频率虽然无法对车体的振动起到最优谐振作用,但是相较于被动式吸振器,磁流变吸振器的固有频率与车体振动频率也很协调,所以可以在一定程度上起到减振作用。

图7 不同吸振器对轨道车辆车体垂向振动的影响Fig.7 Effect of different vibration absorbers on verticalvibration of railway vehicle body
为了更直观的了解到吸振器的吸振能力,将车体振动频段0~3 Hz划分为300个相等的单位长度,利用梯形公式对车体的垂向振动功率谱在有效工作频段内进行加权积分,以所得结果的大小代表车体振动能量,结果越小,则吸振器的吸振能力越好。
设每个单位长度下的能量面积为Si
(19)

定义无量纲数Ecarbody为评价车体能量指标,则
Ecarbody=S0.01·P0.01+…+Si·Pi+…+S3·P3
(20)
式中:Pi为振动频率iHz对车体垂向振动的影响概率,通过对该振动频率与车体垂向振动的相干度进行归一化处理获得,相干度越高,则影响概率越大。由于国内尚未确定轨道不平顺激励频率与车体垂向振动之间的相干度,则假设各振动频率与车体垂向振动的相干度相同,Pi=1/300。
通过上述方法计算,可以对运行速度为60 km/h时各类吸振器吸振能力进行直观比较,如图8所示。由图8可知,车体宽频振动下,磁流变吸振器的吸振能力要优于另外两种被动式动力吸振器。

图8 各类吸振器吸振能力对比图Fig.8 Comparison of various types of absorbervibration absorption capacity
以载客量A、车速V作为变量,通过式(19)、式(20)求出载客量和车速不同时,未利用磁流变吸振器减振的车体垂向振动能量和利用磁流变吸振器减振的车体垂向振动能量,并分别作为z轴, 载客量A作为x轴, 车速V作为y轴,如图9所示。
由图9(a)、图9(b)可知,经磁流变吸振器减振前、后的车体振动能量与载客量及车速之间均呈现复杂函数关系。车体振动能量随着车速的增大而增大、随着载客量的增大而减小,其中车速比载客量对车体的垂向振动具有更大的影响,并且在60~80 km/h的速度区间内,车体垂向振动能量呈现指数式增长,在车速为80 km/h、载客量为空载AW0的情况下车体振动能量达到最大值。因此,60 km/h以上的行车速度会加剧城市轨道交通车辆车体的垂向振动,但如果此时载客量达到满载或超载,可对车体的垂向振动有所抑制。通过图9(a)、图9(b)的对比可以发现,利用磁流变吸振器进行减振后,车体在不同的速度和载客量下的车体振动能量均有所减小,但是还不能从该对比中直观的发现车速或载客量对磁流变吸振器减振效果的影响。因此,需引入动力放大系数ε进行进一步分析。
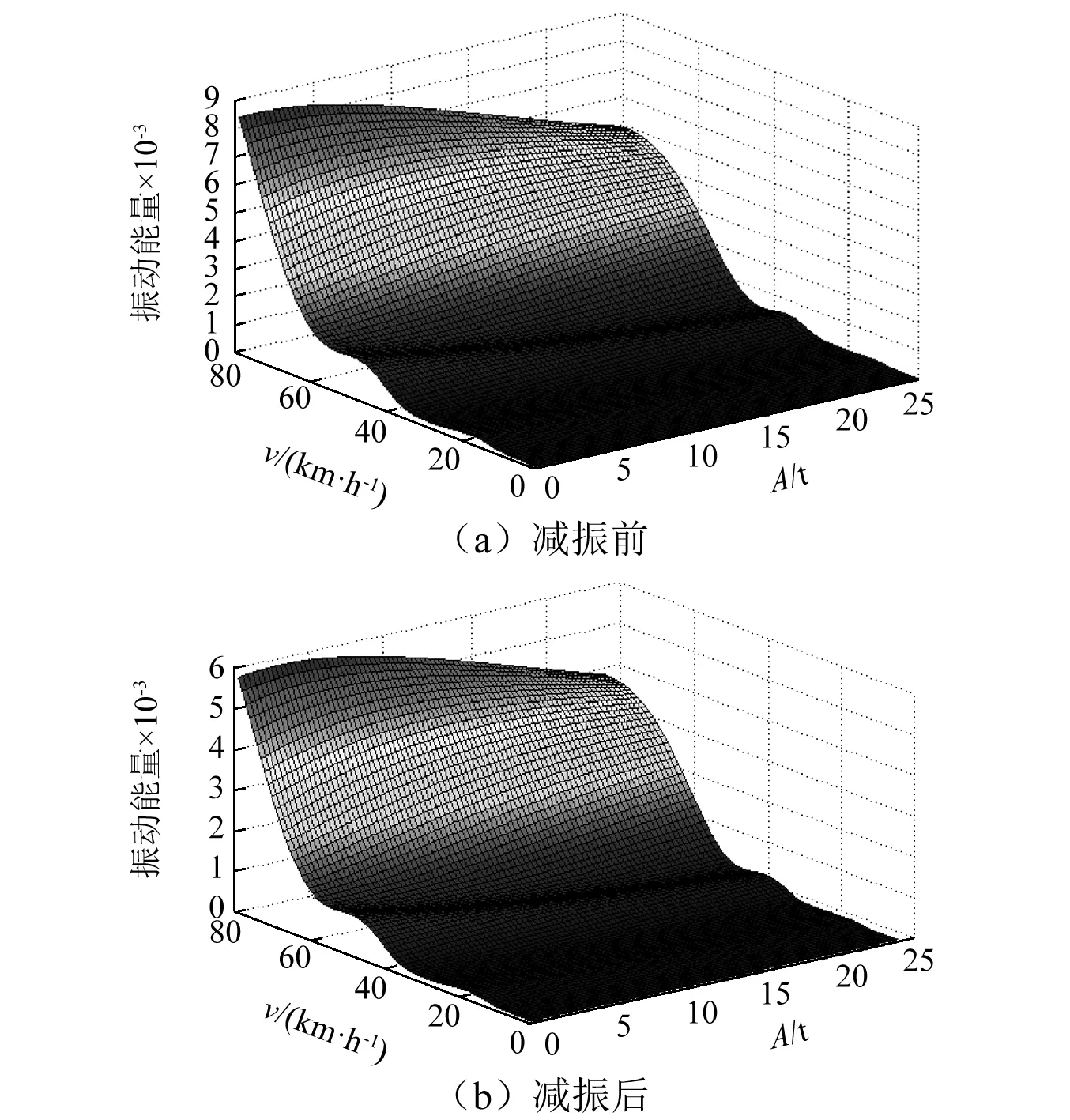
图9 减振前、后的轨道车辆车体垂向振动能量图Fig.9 Vertical vibration energy of railway vehicle bodybefore and after vibration reduction
(21)
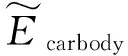
图10为根据式(21)计算获得的不同载客量和车速下,磁流变吸振器与无吸振器的动力放大系数特性。由图10可知:载客量不变时,动力放大系数ε由速度引起的变化量较小在0.05左右,说明速度对磁流变吸振器减振效果的影响不大,这是因为通过第四节的优化设计,可以宽频减振的磁流变吸振器已适应城轨车辆的不同速度工况。但明显可以发现在10 km/h、30 km/h、60 km/h处的磁流变吸振器减振效果更好,这是因为在该速度下,车体呈现多峰值振动,磁流变吸振器宽频减振的优势更加明显。
当速度不变时,载客量引起的变化较大在0.12左右,所以载客量的变化对磁流变吸振器减振效果的影响更大。空载情况下,磁流变吸振器的减振性能最好,ε基本小于0.7,最优时接近0.6,相当于减小了车体近一半的振动能量,而在超载的情况下,ε接近0.77,这表明磁流变吸振器只降低了车体不到1/4的振动能量,这是因为载客量的增加相当于车体质量Mc的增加,即使磁流变吸振器可以根据载客量的变化并通过最佳设计频率表达式调整到最佳减振状态,但磁流变吸振器的质量Md不变,吸振器的吸振能力有限,因此载客量的增加会降低吸振器的减振效果。

图10 磁流变吸振器与无吸振器动力放大系数特性图Fig.10 Characteristics of dynamic magnificationfactor with MRE absorber and no absorber
图10中,在任意载客量和速度下, 动力放大系数ε都小于0.77,这意味着吸振频率针对载客量和车速修正过后的磁流变吸振器可以很好的适用于城市轨道交通车辆,并起到良好的减振作用。
同理, 若Ecarbody取被动式吸振器的车体振动能量,对比磁流变吸振器相较于被动式吸振器的优越性,如图11所示。在图11中,与磁流变吸振器进行对比的被动式吸振器所能吸收的车体振动频率为1.5 Hz。由图11可知,在任意载客量和速度下,动力放大系数ε最大值在0.9左右,最小值接近0.6,这表明磁流变吸振器在任意工况下的减振性能都优于被动式吸振器。图中ε为0.9时,说明磁流变吸振器与被动式吸振器的减振效果十分接近,这是因为此时的车体振动的峰值频率在1.5 Hz左右、与被动式吸振器的工作频率相同,所以被动式吸振器可以发挥良好的减振性能。但从全局角度可以知磁流变吸振器更适用于工况复杂的城市轨道交通车辆。
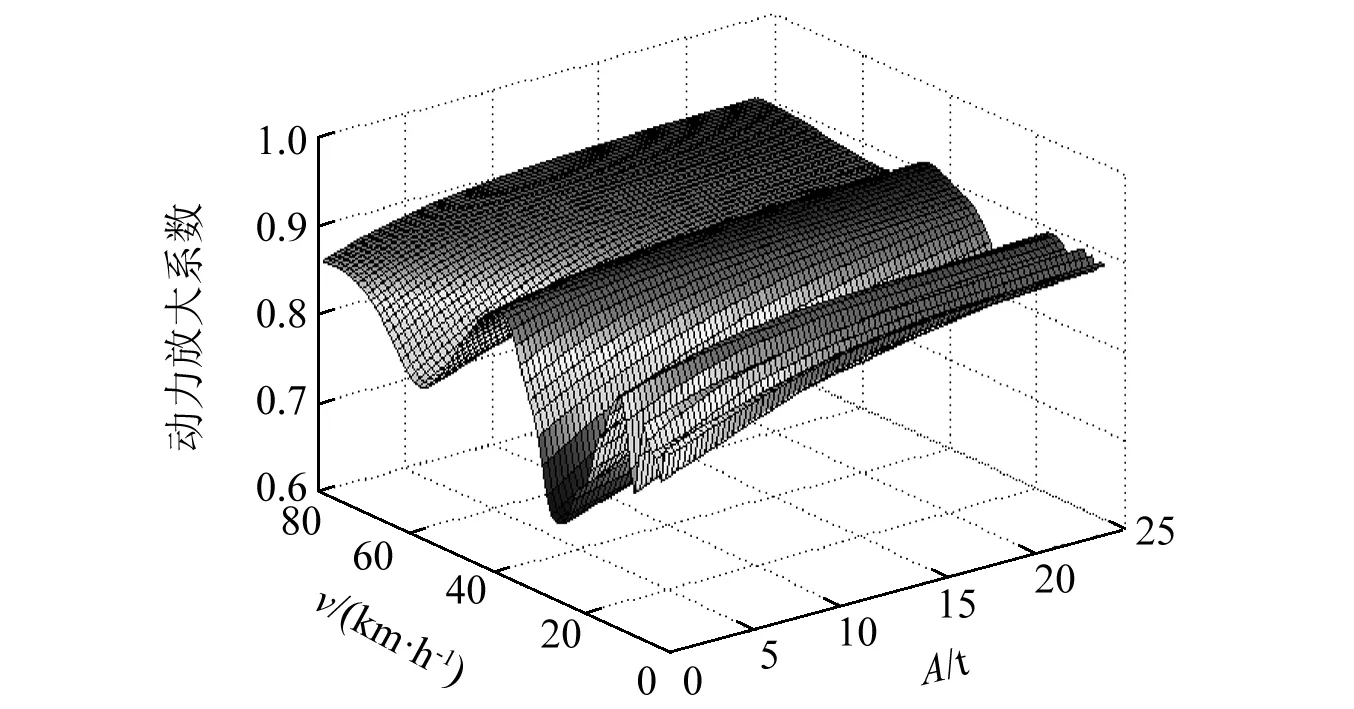
图11 磁流变吸振器与被动式吸振器的动力放大系数特性图Fig.11 Characteristics of dynamic magnification factorwith MRE absorber and passive absorber
6 磁流变吸振器减振能力的验证
目前,各国评定轨道车辆舒适性的指标有很多种,其中国际上较常用的是Sperling平稳性指标[24]。因此,采用Sperling平稳性指标对论文的正确性和可行性进行验证。
图12为空载和超载两种情况下,安装被动式动力吸振器、磁流变吸振器和未安装动力吸振器的车辆Sperling指标对比图,其中被动式吸振器是按80 km/h车速设计的。
由图12可知,随着车速的提高,轨道车辆的运行平稳性指标整体上呈增大趋势,三种状态下的车辆运行平稳性都保持在优级(<2.5)。
图12(a)中,在速度为12 km/h、36 km/h、72 km/h附近,安装被动式吸振器与磁流变吸振器的车辆Sperling指标较接近,这是因为这些速度区间下车体的振动峰值频率与被动式吸振器的工作频率相接近,所以被动式吸振器可以有效的发挥减振作用。图12(b)中,磁流变吸振器与被动式动力吸振器减振能力相接近的速度区间发生微小偏移,这是因为载客量的增加,导致车体振动的峰值频率发生改变,所以被动式吸振器能有效发挥减振作用的速度区间也会发生偏移;此外,安装被动式吸振器和磁流变吸振器的车辆Sperling指标都接近未安装动力吸振器的车辆Sperling指标,说明被动式吸振器和磁流变吸振器的减振效果都在降低,这是因为载客量的增加,使吸振器与车体的质量比相对减小,从而降低了吸振器的减振性能,但是,安装磁流变吸振器的车辆Sperling指标要明显低于未安装动力吸振器和安装被动式动力吸振器的车辆,这说明磁流变吸振器对车辆具有较好的减振作用。因此,总的来说,无论空载和超载工况,通过Sperling平稳性指标的对比,车辆的运行品质时刻保持在优级,证明了磁流变吸振器具有较好的减振能力。

图12 不同类型吸振器下轨道车辆舒适度的Sperling指标Fig.12 Sperling index of the comfort of railway vehiclewith different types of vibration absorbers
7 结 论
(1) 在磁流变吸振器的有效工作频段内,半主动式磁流变吸振器在车体的各振动频率点的吸振能力都优于被动式吸振器,其宽频减振优势明显;在有效工作频段外,磁流变吸振器也可以起到一定的减振作用,因此,磁流变吸振器具有较好的轨道车体减振特性。
(2) 为了要提高动力吸振器的减振效果,提出了适用于城轨车辆的利用磁流变弹性体的动力吸振器设计方法。首先要确定磁流变吸振器和主振系的质量比,然后确定吸振器的有效工作频段,最后,获得磁流变吸振器的设计频率,从而提升动力吸振器的减振能力。
(3) 针对城市轨道车辆的客流量及车速变化频繁的特点,利用多元回归分析法拟合了半主动式磁流变吸振器的最佳设计频率表达式,利用磁流变弹性体材料刚度可调、固有频率可变的特点,使吸振器与车体始终处于谐振状态,可最大程度的发挥磁流变吸振器的减振作用。

