柔性平面3-RRR并联机器人耦合动力学及模态特性研究
盛连超, 李 威, 王禹桥, 范孟豹, 杨雪锋
(中国矿业大学 机电工程学院,江苏 徐州 221116)
相对于串联机器人,并联机器人具有高速度、高加速度、高承载能力、低能耗、无累积误差、精度高等优点,被广泛用于航空航天、精密光学仪器、生物工程操作、精密加工机床等领域[1-5]。
随着社会的发展,高速高效、轻型低耗成为当今全球机械产品的重要标志和发展趋势[6-8],但轻型化的柔性并联机器人在高速带载情况下运行时,由于惯性力等诸多因素,各柔性杆件极易产生弹性变形,导致机器人的整体动态性能下降,影响其正常工作[9-11]。如应用在食品包装中的拾取类并联机器人[12]及农业采摘机器人[13-14]。
为了解决这个问题,首先要建立柔性并联机器人动力学模型[15],徐晗[16]、余跃庆[17]、张清华[18]、张绪冲[19]分别采用不用方法,考虑不同因素建立了平面3-RRR平面并联机器人的动力学模型。 Sharifnia[20],Zhang等[21-22]采用假设模态法分别对柔性3-PSP和平面3-RRR并联机器人建立了动力学模型。
然而通过目前的研究发现,简单的动力学模型极易产生过大的误差,而精确度较高的模型往往特别复杂,导致后续振动控制难度较大甚至无法实施。因此选取合适的动力学建模方法,考虑实际边界条件及影响因素,建立既能保证高精确度,同时又能方便求解的动力学模型具有重要的研究意义。针对上述存在的问题,本文考虑系统刚柔耦合效应及柔性中间连杆两端集中转动惯量影响,选取动态参数相对较少,基于系统模态特性为建模基础的假设模态法为建模方法,通过拉格朗日方程建立平面3-RRR并联机器人耦合动力学模型,并与有限元软件(ANSYS)分析及模态试验结果作比较,结果表明文中所建立动力学模型能够有效反映系统主要振动模态,并能充分反映惯性力和耦合力对系统模态特性的影响,这对后续的振动控制及结构优化设计提供了有力的参考依据。
1 柔性3-RRR平面并联机器人系统概况
柔性平面3-RRR并联机器人的系统构成及坐标系如图1所示,系统由末端运动平台C1C2C3,固定支撑平台A1A2A3,三条连接末端运动平台和固定支撑平台的支链A1B1C1,A2B2C2,A3B3C3组成,且三条支链完全相同,即A1B1=A2B2=A3B3,B1C1=B2C2=B3C3,通过转动副将驱动连杆与柔性中间连杆以及柔性中间连杆与动平台进行连接,其中A1、A2、A3是驱动关节,杆长A1B1=A2B2=A3B3=B1C1=B2C2=B3C3=210 mm,末端运动平台上关节所在圆的半径为R=68 mm。在三个驱动电机的驱动下,该并联平台可以完成沿x轴方向和y轴方向的平动运动以及绕z轴方向的转动运动的三自由度运动。
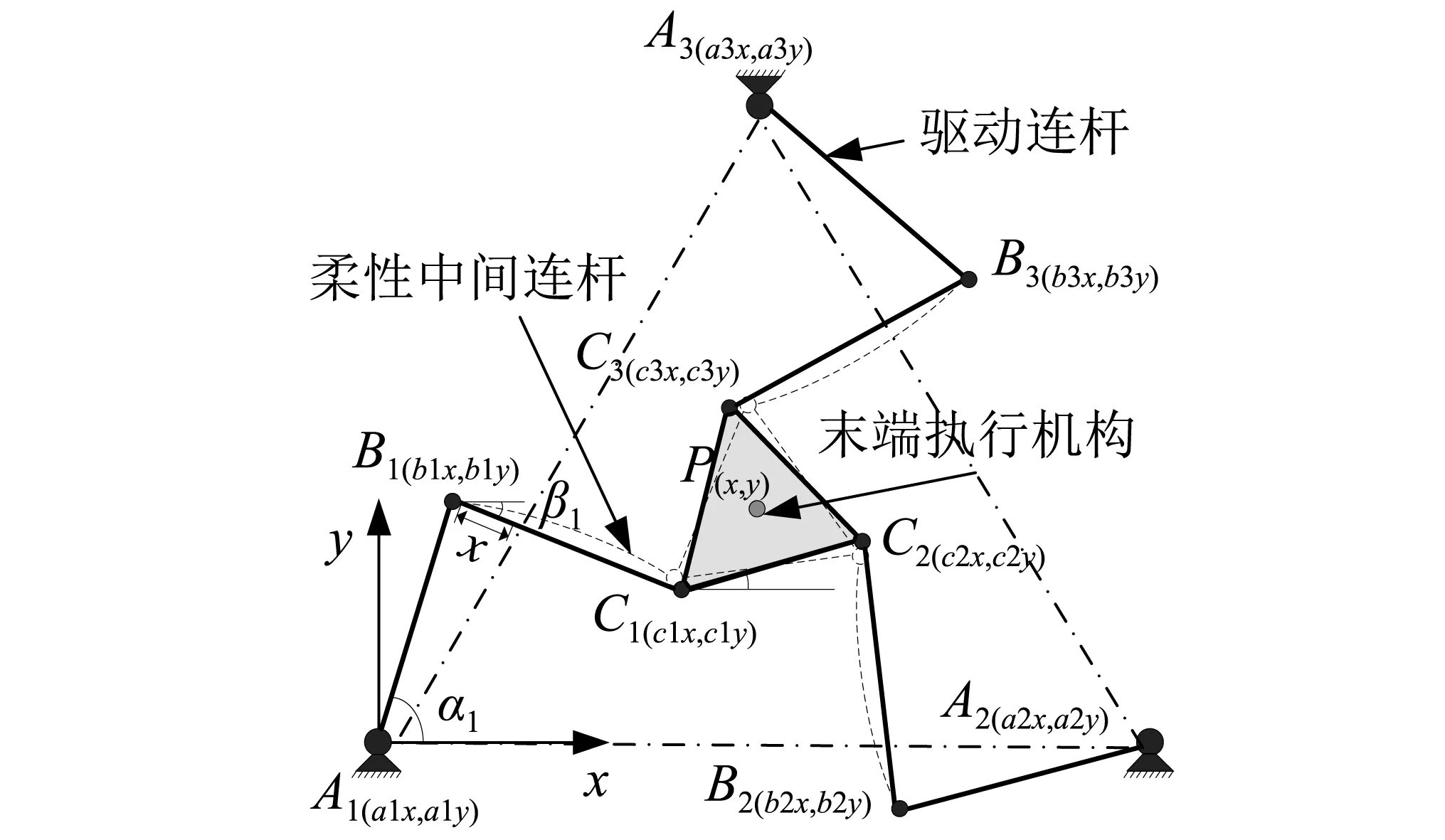
图1 柔性平面3-RRR并联机器人平面示意图Fig.1 The structure diagram of the flexible planar 3-RRR parallel robot
在实际结构中,一般情况下驱动连杆横截面积尺寸较大以保证其刚度,而柔性中间连杆截面积尺寸较小以减轻其质量。柔性平面3-RRR并联机器人的具体材料、尺寸参数如下,加工材料为铝合金7075,材料的弹性模量为E=7.1×1010N/m2,密度为ρ=2.81×103kg/m3,主动杆的长宽厚分别为210 mm,25 mm,10 mm,柔性中间连杆的长宽厚分别为210 mm,25 mm,5 mm,柔性中间连杆两端的集中转动惯量JBi=JCi=2.2×10-3kg/m2,截面惯性矩Ii=2.6×10-10m4。
机构的振动主要是由电机驱动、惯性力和移动平台的有效载荷造成的。为了进一步确定系统的振动情况,减小不必要的计算,提高计算速度,应对柔性并联机器人的模型作简化。考虑到柔性并联机器人的运动部件只有各运动支链和动平台,电机、减速器及其支架等都固连在底座上,实际中为保证运行平稳,刚度支撑等要求,底座设计得比较厚重,这里可以将除运动支链和动平台之外的部件视为固定,运动支链的主动杆的电机驱动端视为与基座固定,同时,对各支链和动平台上的倒角、圆角、非必要的孔等特征也进行简化,简化后的柔性平面3-RRR并联机器人有限元(ANSYS)仿真结果如图2所示,前四阶振动频率分别为66.894 Hz、68.289 Hz、85.716 Hz、122.57 Hz,通过前四阶振型发现,发生弯曲的部位主要集中在柔性中间连杆部分,第四阶振型显示,柔性中间连杆不仅发生弯曲甚至发生扭转,这将直接导致末端运动平台的倾覆,影响末端运动平台的操作精度和质量,因此如何控制中间连杆的振动以及找出其共振频率就显得非常重要,这也为提高末端运动平台操作精度和质量打下坚实的基础。
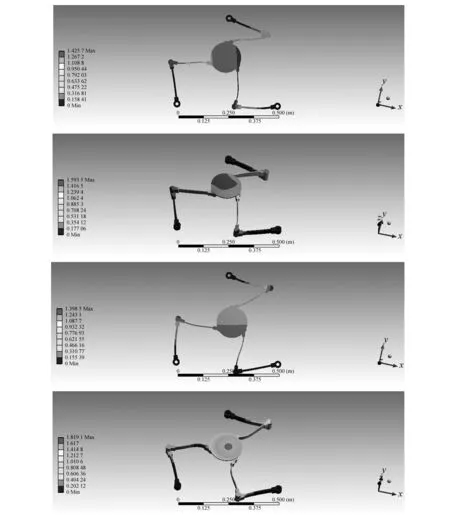
图2 柔性平面3-RRR并联机器人的前四阶振型Fig.2 The first four mode shapes of flexible planar 3-RRR parallel robot
2 动力学建模与数值仿真
2.1 有限元分析法
在有限元分析软件(ANSYS)中建立柔性中间连杆的物理模型,材料选择铝合金,柔性中间连杆两端边界条件设置为铰支,并定义为柔性接触,同时考虑两端集中质量和转动惯量的影响。仿真分析结果如图3所示, 柔性中间连杆前两阶振动频率分别为53.18 Hz,204.07 Hz。
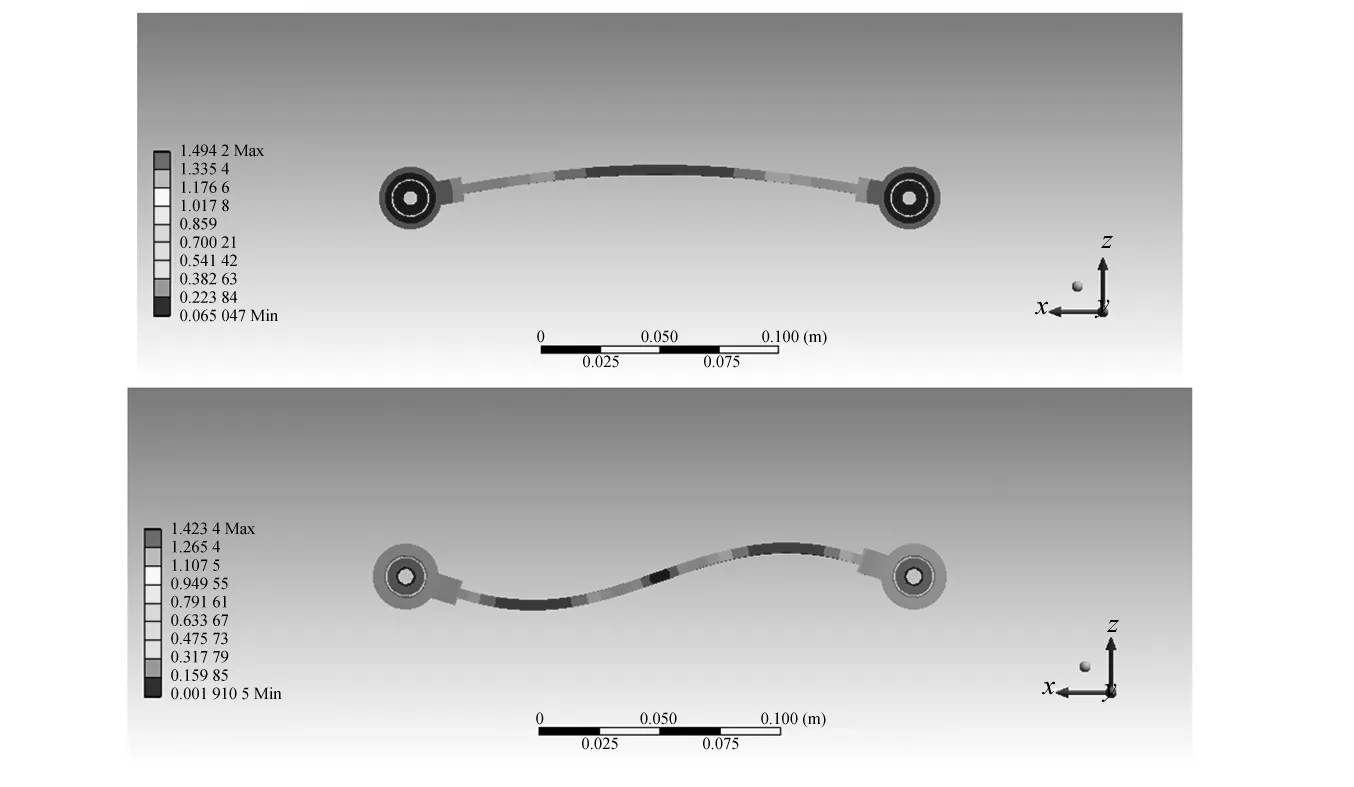
图3 柔性中间连杆前两阶模态振型Fig.3 The first two mode shapes of flexible intermediate link
2.2 假设模态法
基于有限元(ANSYS)分析的结果,如图2所示,驱动连杆的振动幅值要远小于中间连杆的振动幅值,因此在建模过程中只把中间连杆作为柔性杆处理,而其他构件均视为刚性构件。机器人系统坐标如图1所示,其中给出了柔性中间连杆的变形和不变形两种状态。在建模过程中,做如下假设:①基于Euler-Bernoulli梁模型分析柔性中间连杆系统动力学特性,只考虑柔性中间连杆在运动方向的横向振动;②相对于柔性中间连杆的长度,其横向变形是小变形,所以方程可被线性化处理;③忽略重力的影响。为了与上述有限元(ANSYS)分析作对比,建模过程中柔性中间连杆尺寸、材料等因素均与上述有限元(ANSYS)分析法中的条件一致。考虑柔性中间连杆两个末端轴承引入集中转动惯量的影响,基于假设模态法,建立系统耦合动力学模型。
第i根柔性中间连杆的变形可以表达为:
(1)
式中:φij(x)为模型的振型函数;qij(t)为时间变化的模态幅度;r代表所选的假设模态。
每个柔性中间连杆都被看作是Euler-Bernoulli梁,末端运动平台和驱动连杆均被看作刚体,柔性中间连杆的边界条件采用两端铰支的约束方式,所以,振型函数φij(x)可以表示为:
φij(x)=sin(jπx/L)=sin(jπξ)=φij(ξ),j=1, 2, …,r
(2)
式中:ξ=x/L,r代表所选的假设模态,驱动连杆和柔性中间连杆的杆长均为L,x是柔性中间连杆上任意一点到Bi点的距离。
为了获得柔性中间连杆的动力学方程,与Lagrange方程联合建模,因此需要先求得系统的动能和势能。系统的总动能包括驱动连杆、柔性中间连杆和末端运动平台的动能,见式(3)。
(3)
当柔性平面机器人运动时,重力沿着z轴方向并穿过一个x-y平面,所以机器人重力造成的势能并不发生改变。系统的势能是由柔性中间连杆的变形造成的,可表示为:
(4)
式中:Ei和Ii分别代表第i根柔性中间连杆的弹性模量和截面惯性矩。
将系统动能和势能代入拉格朗日第二类方程
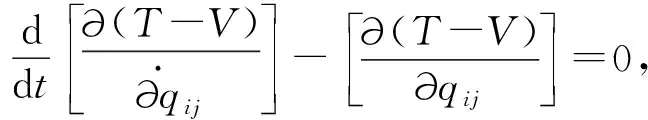
(5)
整理后为:
(6)
将其写成矩阵形式:
(7)
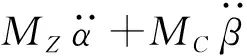
因此第i根柔性杆件的第j阶响应可以表示为,
(8)
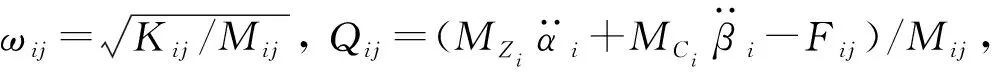
(9)
根据Duhamel积分求解上述方程,则其响应为
(10)
假定柔性并联机器人末端执行器的运行轨迹为半径60 mm的圆,xp=60-60cos 20πtmm,yp=60sin(20πt) mm。由于三根柔性中间连杆的参数一致,本文以柔性中间连杆1为例,研究其动态特性,柔性中间连杆1中点前两阶响应的运动仿真结果,图4所示。
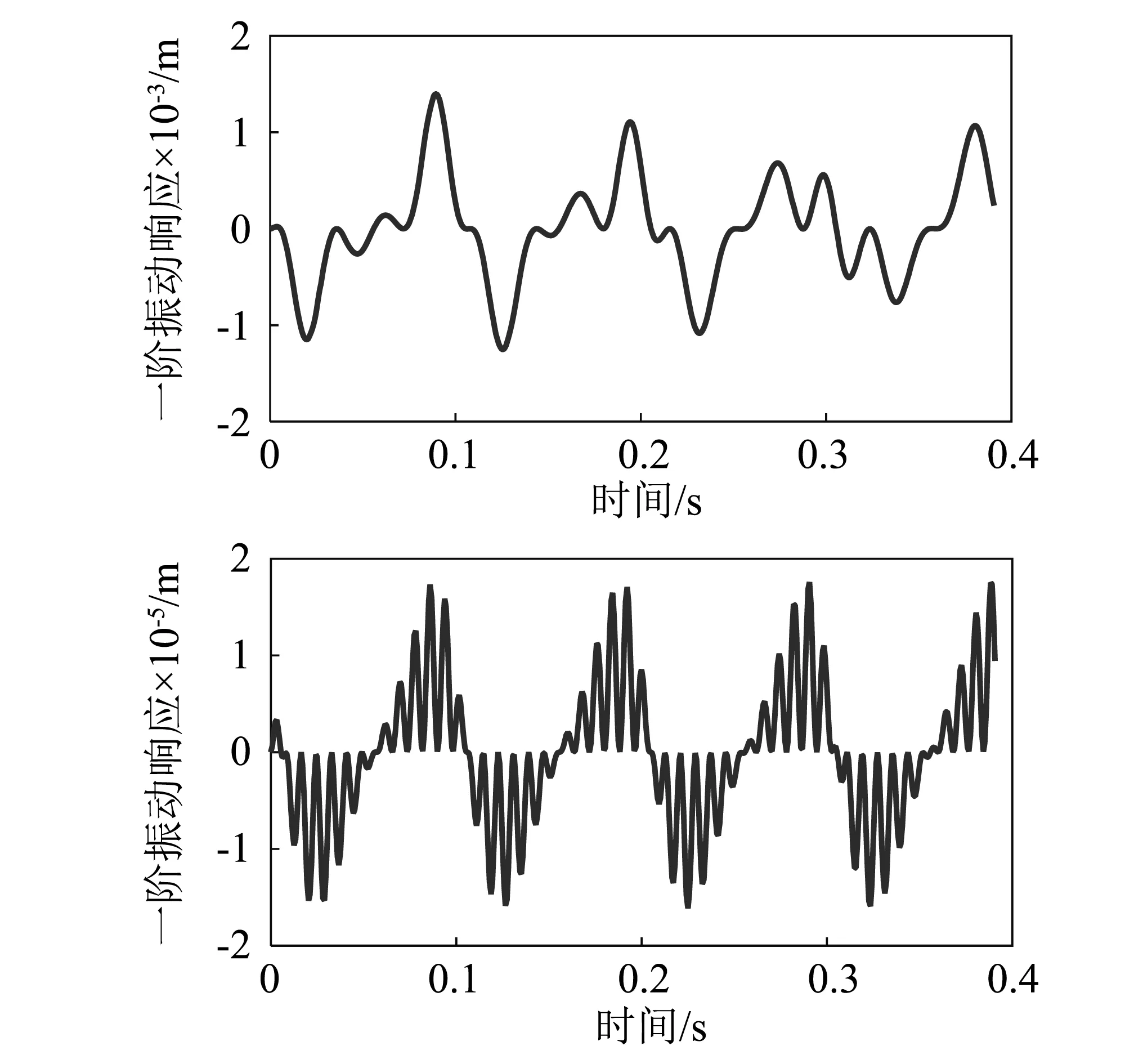
图4 柔性中间连杆1中点处的前两阶响应Fig.4 The first two elastic vibration deformation at midpoint of the first intermediate link
通过图4中得到的柔性中间连杆1中点处前两阶曲线可以看出柔性中间连杆的一阶振动响应幅值明显高于二阶振动响应幅值,柔性中间连杆的振动响应是机器人在工作运行过程中产生振动的一个表征,为了进一步研究其振动特性,确定振动产生的频率,降低对机器人整体性能的影响,通过快速傅里叶变换将柔性中间连杆1中点处的一阶响应特性从时域转化到频域中,如图5所示。
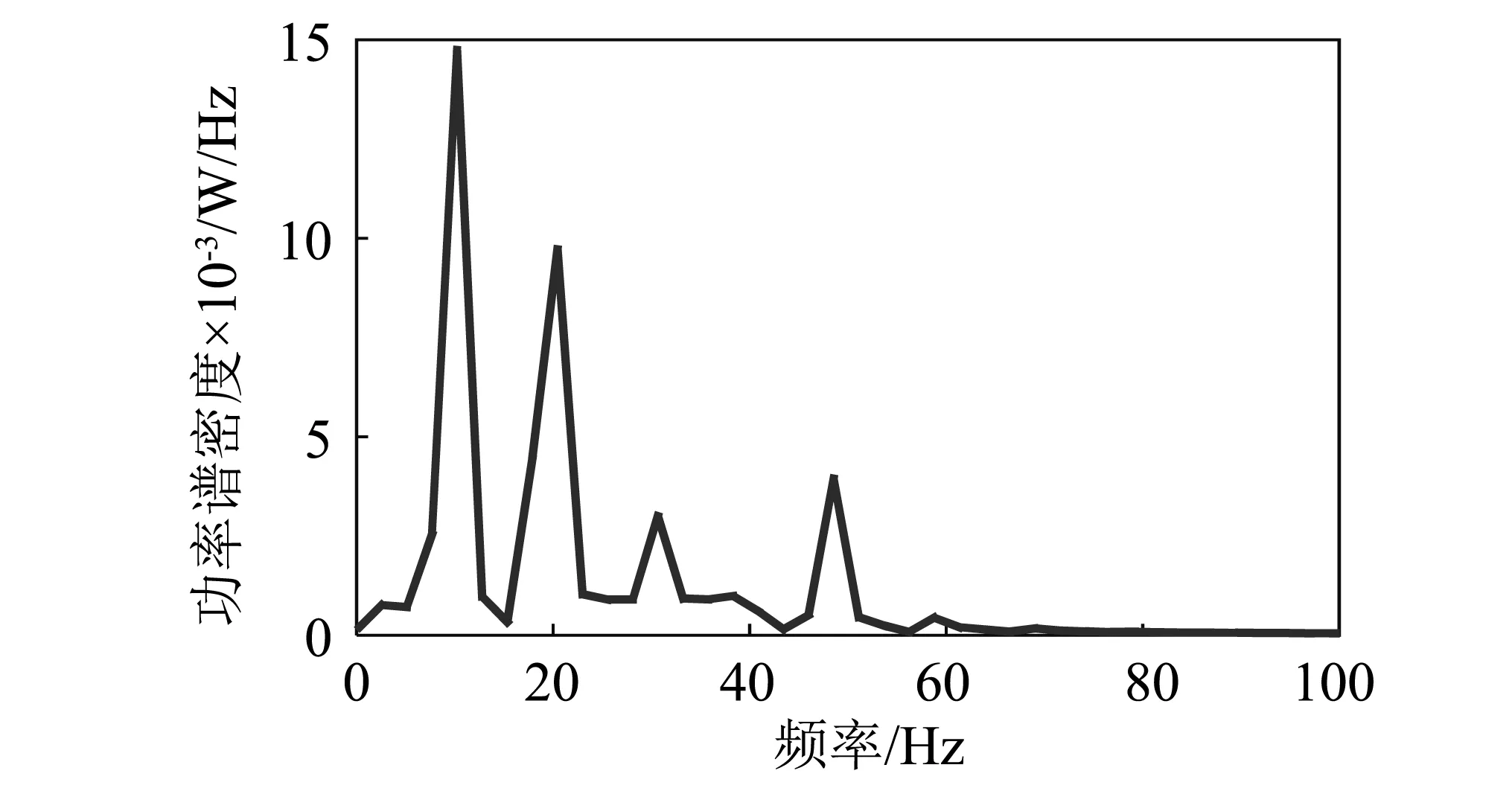
图5 柔性中间连杆1中点处的第一阶振动响应FFT变换Fig.5 FFT of the first order elastic vibration of the first intermediate link
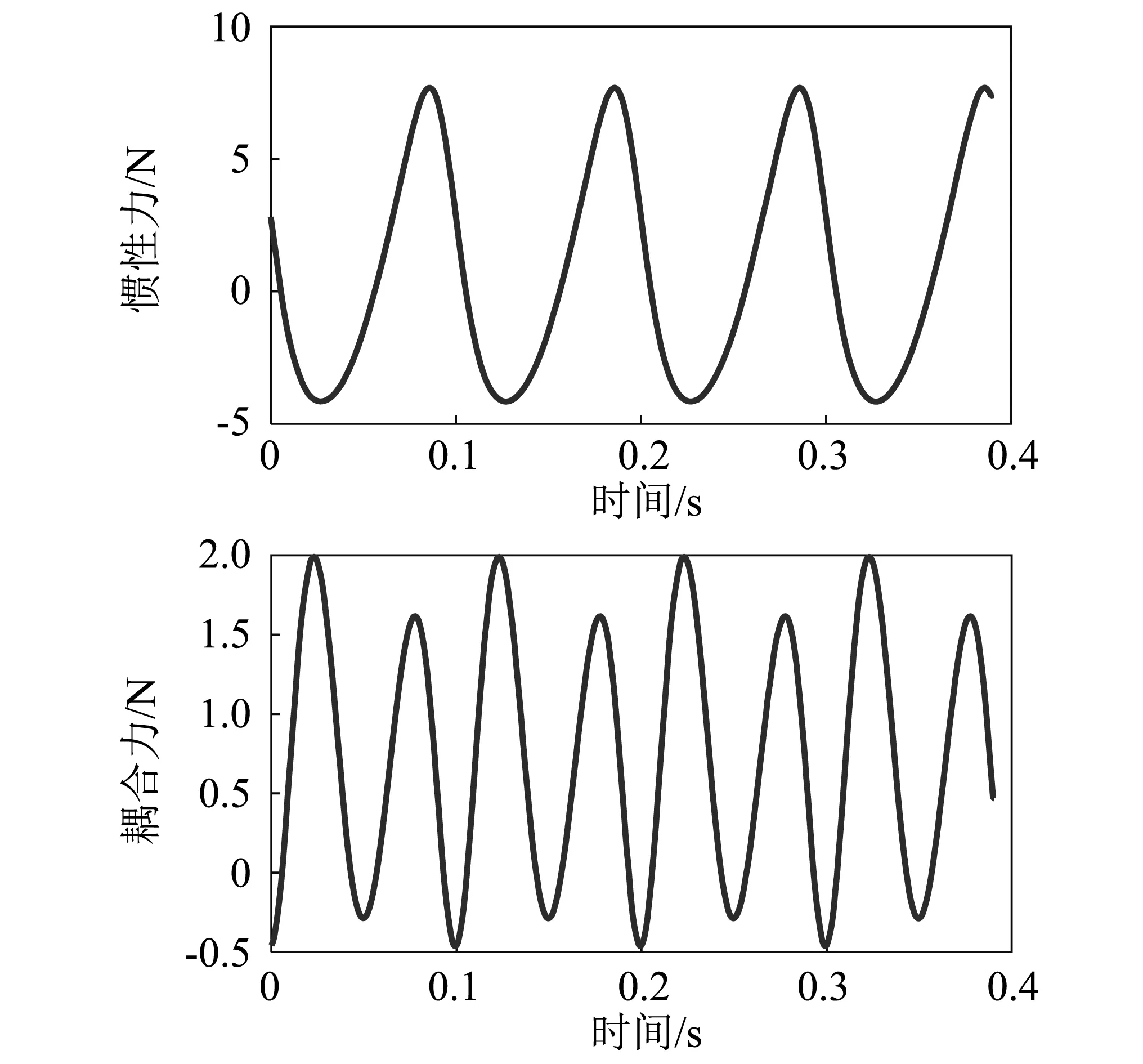
图6 柔性中间连杆所受惯性力和耦合力Fig.6 The inertial force and coupling force of the first intermediate link
从图5中可以看出其振动频率主要集中在10 Hz,20 Hz,30 Hz和48.5 Hz附近,根据公式(6),可以算出柔性中间连杆在考虑转动惯量的情况下的前两阶自由振动频率分别为48.5 Hz,212.6 Hz,通过公式(6)还可以发现,除了自由振动,柔性中间连杆还受到惯性力和耦合力的作用产生强迫振动,惯性力和耦合力随时间的变化曲线,如图6所示。
为了进一步研究其振动频率,将惯性力和耦合力动态响应曲线进行快速傅里叶变换,得到频域特性,如图7所示。
从图7中得到的结果发现,10 Hz,20 Hz,30 Hz为惯性力和耦合力共同引起的强迫振动频率,这也意味着48.5 Hz和212.6 Hz为其一阶和二阶自由振动频率。
3 实验验证与对比分析
为了比较两种动力学分析方法的准确性和实用性,搭建如图8所示的实验台,在实验过程中,将三个驱动电机锁紧在初始位置,末端运动平台在中心位置 ,柔性中间连杆均匀布置7个测点,其中测点1和7在轴承处不作测量,采用多点激励一点拾振的测试方法,将加速度传感器粘贴在固定测点3处,用力锤分别敲击测点2到测点6,所测数据通过与DH5927N动态测试仪连接的加速度传感器和力锤采集,为了使结果更具真实性,每个测点测试5次,取平均值作为试验结果,采集数据由DH5927N动态测试仪记录,采集记录完成后,采用Polylscf分析法分析其动态响应,测点2到测点6的频响特性曲线结果如图9所示。分析结果发现一阶频率和阻尼比分别为49.992 Hz和0.043,二阶振动频率和阻尼比分别为277.813 Hz和 0.022。根据所得试验结果表明,基于文中所建动力学模型得到的前两阶振动频率分别为48.5 Hz,212.6 Hz,与有限元(ANSYS)得到的前两阶振动频率53.18 Hz, 204.07 Hz相比,文中所建动力学模型得到的前两阶固有频率更接近模态试验结果,特别是一阶固有频率基本一致,因此文中考虑刚柔耦合因素及柔性中间连杆两端集中转动惯量所建立的动力学模型能较好的反映出柔性平面3-RRR并联机器人柔性中间连杆的主要振动模态,也证明了此方法更准确,同时也证明了10 Hz,20 Hz,30 Hz的振动频率不是系统本身拥有的频率,而是在运动过程中惯性力和耦合力产生影响引起的强迫振动频率,二阶固有频率产生较大误差的主要原因主要是两种方法在建模过程中的简化处理,弱化了结构体对柔性中间连杆固有频率的影响,对比两种动力学分析方法,文中通过数学方法所建立动力学模型在分析带有柔性中间连杆刚柔耦合系统的固有频率及刚柔耦合效应时有更高的精度,同时由于动态参数较少,方便依托动力学模型的控制器设计。
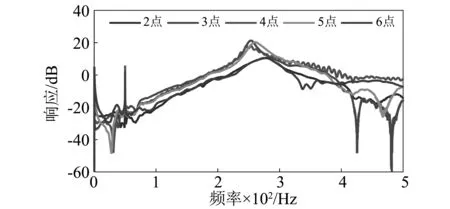
图9 振动响应模态试验结果Fig.9 The vibration response results of modal experiment
4 结 论
(1)相对于有限元分析软件(ANSYS),本文基于假设模态法所建立的耦合动力学模型能够反映集中转动惯量及刚柔耦合效应对系统动态特性的影响,与实际更符。
(2)考虑中间连杆端部集中转动惯量和刚柔耦合效应的影响,文中建立的耦合动力学模型可以分析耦合力和惯性力对柔性中间连杆模态特性的影响,研究结果发现,惯性力和耦合力会导致强迫振动,其频率为10 Hz,20 Hz,30 Hz。
(3)文中所提出的刚柔耦合动力学建模方法适用于各种刚柔结合的柔性并联机器人,所得模型精度高、易求解,解决了动力学模型复杂性问题,对需要以动力学模型为依托的控制器具有指导意义。

