基于流动坐标系的3维空间动力非线性有限元方法
王 涛, 刘德贵, 胡安杰
(西南科技大学 土木工程与建筑学院,四川 绵阳 621000)
对于土木工程大跨度空间结构,特别是大跨度桥梁,如:斜拉桥、悬索桥,考虑几何非线性的有限元计算方法在结构分析中的有着重要的应用。
关于几何非线性,最常用的是以结构变形前为参考建立平衡方程的全量拉格朗日法(TL列式)和以结构变形后为参考建立平衡方程的更新拉格朗日法(UL列式)。Bathe等[1]首先建立了三维梁单元大位移、大转动、小应变UL列式分析方法。陈政清等[2]详细研究了基于UL列式的非线性有限元方法并将其运用到了实际工程的计算中。
目前,大多数成熟的商业有限元软件如ANSYS,通常都采用UL列式。但对于大转动问题,为了在计算中得到更精确的结果,使用UL列式往往需要增加荷载分级加载步数,显著增加了计算时间,且由于在非线性分析时材料本构关系与单元的运动描述紧密耦合,UL列式方法的推导过程通常都非常繁琐,在实际编程的应用中难度相对较大,这也引起了国内外广大学者对该问题其它解决途径的研究兴趣。算法简单可靠、编程方便、非线性计算收敛性与稳定性好的流动坐标系方法(共旋坐标系),以下称为CR列式法(Co-rotational Formulation)成为了结构几何非线性有限元计算方法研究的另一关注点。
Wempner[3]最早提出了基于CR列式几何非线性的算法概念,即:认为结构是处于大变形、大位移、小应变状态,通过扣除刚体位移来得到有限元模型单元节点实际位移,该方法是一种“几何精确”的算法,具有算法相对简单、力学概念明确等的优点。Crisfield等[4]针对实体、壳、梁单元的几何非线性CR列式提出了一致列式方法。Felipppa等[5]对梁单元的CR列式的计算方法进行了深入研究。
Zhang等[6]使用CR列式非线性有限元方法计算了整体张拉结构的大位移问题,Liang等[7]基于CR列式有限元方法分析了结构的非线性扭转问题,邓继华等[8]开发了基于CR列式并考虑徐变作用的非线性杆、梁单元,潘永仁等[9]基于CR列式几何非线性计算方法开发了有限元计算程序并运用到了大跨度悬索桥施工过程监控的计算中。
上述研究均主要关注的是CR列式在结构静力几何非线性计算中的应用。目前,在工程结构的动力时程计算中,很多时候使用振型分解法或线性的Newmark-β法来得到结构的振动响应。对于结构的小幅度振动,线性计算方法尚能达到满足工程要求的计算精度,但当大跨度柔性结构在3维空间发生较大幅度振动时(特别是索结构),振动往往是非线性的,使用线性计算方法得到的计算结果很可能与实际情况偏差较大。康厚军等[10]也在其研究中指出,对于像斜拉桥这样的结构,构建高效、可靠的全桥非线性振动计算大系统是桥梁工程学未来发展必须关注的研究方向。吴庆雄等[11]针对索梁结构非线性振动建立了有限元计算方法,开发了计算程序,但文中算法是建立在结构静力平衡状态上的,计算中不能直接考虑结构非线性振动时的重力变化,也没有考虑端点强制位移激励作用下的非线性振动计算方法。曹九发等[12]建立了使用完全拉格朗日方法(TL列式)的非线性动力有限元程序,分析了大型风力机的几何非线性动态响应,但TL列式始终以结构的初始构型为参考,很多情况下,为了简化推到过程,计算使用的非线性切线刚度矩阵本身也是近似的,当柔性结构具有较大的振动位移时,计算结果可能与实际情况呈现较大偏差。
为了在动力时程计算中模拟工程结构发生大幅振动时的几何非线性效应,本文基于CR列式首先建立了考虑初始应力的3 维空间中非线性杆、梁单元,然后开发了考虑几何非线性的CR列式Newmark-β动力时程计算方法,编制了通用的非线性动力计算程序(使用杆、梁单元),通过与ANSYS计算对比,验证了本文算法具有较快的计算速度且编制的程序具有良好的可靠性、稳定性,适用于作为大跨度桥梁结构(斜拉桥、悬索桥)几何非线性振动研究的基础计算方法。
2 基于CR列式杆梁结构几何非线性计算原理
2.1 三种坐标系统
根据潘永仁等人的论述,本文认为,基于CR列式非线性有限元算法的核心问题在于建立与有限元模型单元相关的3种坐标系统(即:结构建模总体坐标系、单元随动坐标系、单元端截面随动坐标系)以及处理它们之间的关系。由于直杆单元属于梁单元的退化情况,所以这里以3维梁单元为例来阐述杆、梁单元中3种坐标系之间的关系。
(1)结构总体坐标系
如图1所示,结构总体坐标系用xi(i=1, 2, 3)表示(对应X,Y,Z轴),其基矢量为ei(i=1, 2, 3), 总体坐标系始终不变,结构的建模与最终计算得到的模型节点位移,均依据总体坐标系来描述。
(2)单元随动坐标系
如图1所示,为了得到空间梁单元的单元局部坐标与整体坐标系的关系。这里定义梁单元的单元随动坐标系。单元随动坐标系描述了整个梁单元在3维空间中的位置。
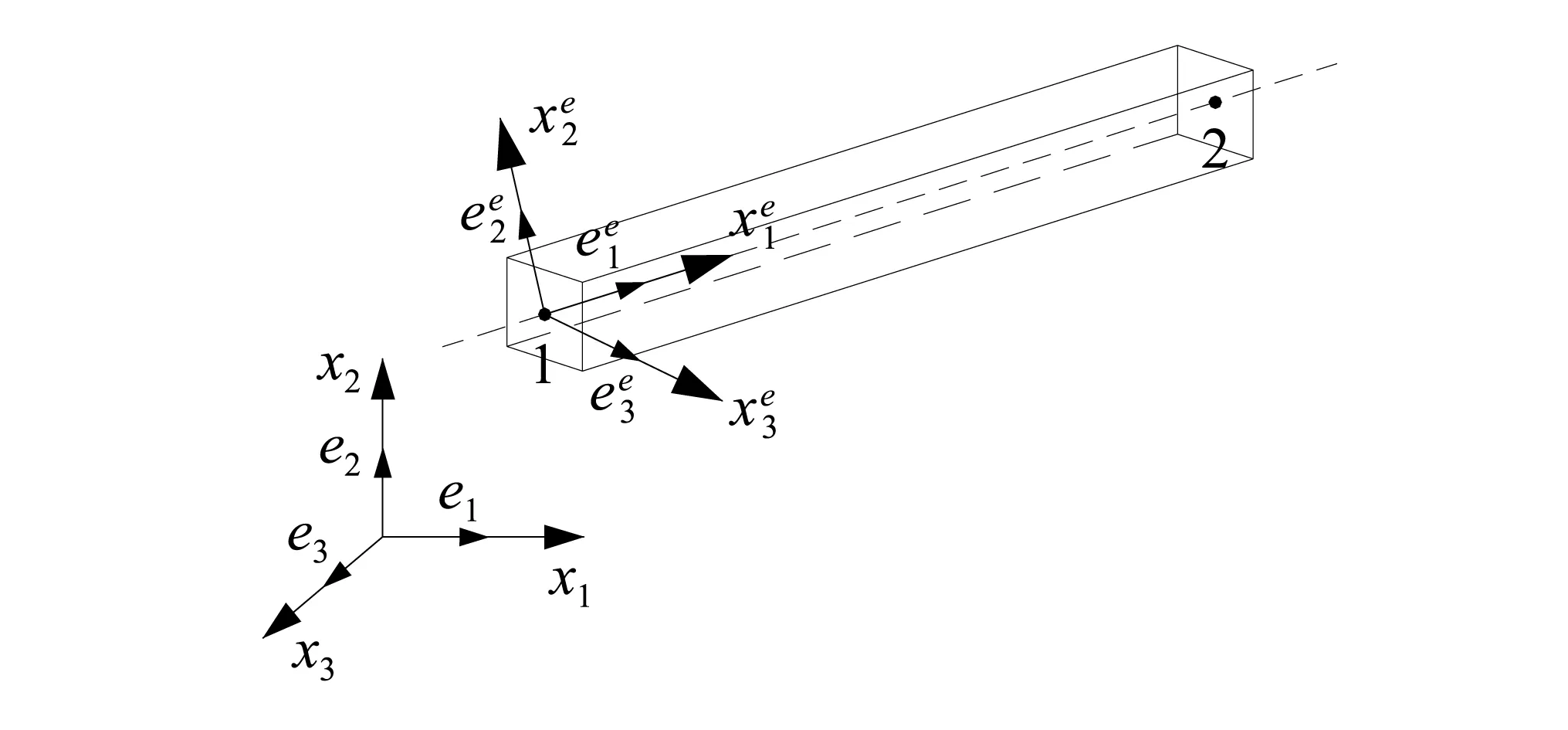
图1 总体坐标系与梁单元随动坐标系Fig.1 The global coordinate system and co-rotationalcoordinate system of beam element
(3)单元端截面随动坐标系

图2 总体坐标系与梁单元端截面随动坐标系Fig.2 The global coordinate system and co-rotationalcoordinate systems of the cross section of beam element


1.2 单元变形后随动坐标系的计算
对于大变形梁单元,要得到正确的单元节点力,关键在于计算单元在3维空间中的伸长,以及梁端截面的转角和单元变形后的单元随动坐标系。
(1)欧拉有限转动公式
对于3维空间矢量旋转,本文使用欧拉有限转动公式[9]。如图3所示,矢量R的初始位置用OP来表示,按照右手定则,沿着转动轴ON逆时针旋转了θ角成为R′,ON方向用单位矢量n来表示,垂直于转动轴过N点的平面如图3(b)所示。
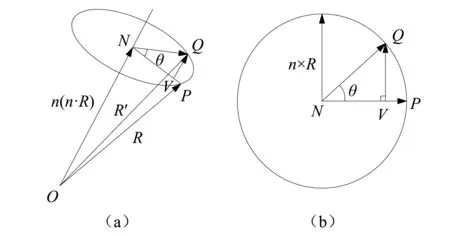
图3 有限转动矢量示意图Fig.3 The schematic figure of finite rotation vector
根据图3中各个矢量的关系可以求出R′:
ON=n(n·R)
NP=R-n(n·R)
R′=ON+NV+VQ
即:
R′=Rcosθ+n(n·R)(1-cosθ)+(n×R)sinθ
(1)
(2)单元端截面随动坐标系的计算
已知在t至t+Δt时刻,在结构坐标系中单元节点发生了转动位移矢量Δθji,平动位移矢量ΔUji,j=1,2;i=1, 2, 3。
根据Δθji由数学定义可知转动角度值为:
(2)
则各节点的转动轴矢量方向为:
(3)
(3)单元随动坐标系的计算
设t时刻在总体坐标系下,单元节点坐标为tXji,则可以得到t+Δt时刻节点坐标为:
t+ΔtXji=tXji+ΔUji,j=1, 2;i=1, 2, 3
(4)

(5)

(6)
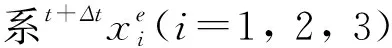
1.3 单元随动坐标系中单元变形的计算
在t+Δt时刻单元变形可以分解为:弯曲变形,扭转变形,伸长变形。
(1)弯曲变形

(7)
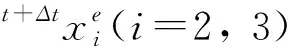
(2)扭转变形

(3)伸长变形
在潘永仁的研究中,将单元的伸长变形定义为薄膜变形,通过定义单元变形曲线并计算曲线弧长变化来得到单元的薄膜变形。
本文认为,对于一般的几何非线性计算,根据小应变假设,从直观上来看可以由节点的位置直接计算得到单元的伸长变形值。
已知t时刻单元节点位置为tXji,则可以计算得到t时刻单元长度为
(8)
根据式(4)得到总体坐标系下t+Δt时刻节点坐标t+ΔtXji,与式(8)方法相同计算t+Δt时刻单元长度t+Δtl可以得到
Δl=t+Δtl-tl
(9)
Δl即为t+Δt时刻单元的伸长值。
1.4 节点位移计算
(1)单元节点力的计算
根据1.2节与1.3节中的计算原理,可以得到在单元随动坐标系中单元变形后t+Δt时刻的单元节点位移向量ue,由于单元随动坐标系原点在单元节点1上,所以ue可写为
ue=[0 0 0θ11θ12θ13Δl0 0θ21θ22θ23]
(10)
单元随动坐标系中单元实际内力为:
fe=keue
(11)
式中:fe为单元内力的节点力向量;ke为单元弹性刚度矩阵。对于直杆单元,流动坐标系内单元的位移只有沿轴向的伸长而无转动,在流动坐标系ke内取为杆单元的线弹性刚度矩阵即为“几何精确的”; 对于梁单元,一般情况下考虑结构几何非线性计算时,通过CR列式方法,扣除单元刚体转动后,可以认为梁单元是处于大变形、大转动、小应变状态的,那么在单元的局部流动坐标系内,则可以认为力与位移的关系是近似线性的,ke可以近似取为梁单元的线弹性刚度矩阵。
(2)单元坐标转换矩阵与应力刚度矩阵
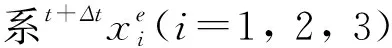
当单元中存在初始轴力时,单元的转向与侧向变形会导致单元产生应力刚度矩阵,在杆梁单元的线性计算中,单元应力刚度矩阵通常是必须考虑的,而在非线性计算中,单元应力刚度矩阵仅用来组集总体切线刚度矩阵,加快迭代收敛。3维空间杆、梁单元应力刚度矩阵的表达式可参考文献[13-14]。
(3)节点位移计算
在静力非线性计算中,总体结构在外力作用下变形后的总体节点内力向量可表示为R(u),为位移的非线性函数,总体节点内力向量流程,如图4所示。
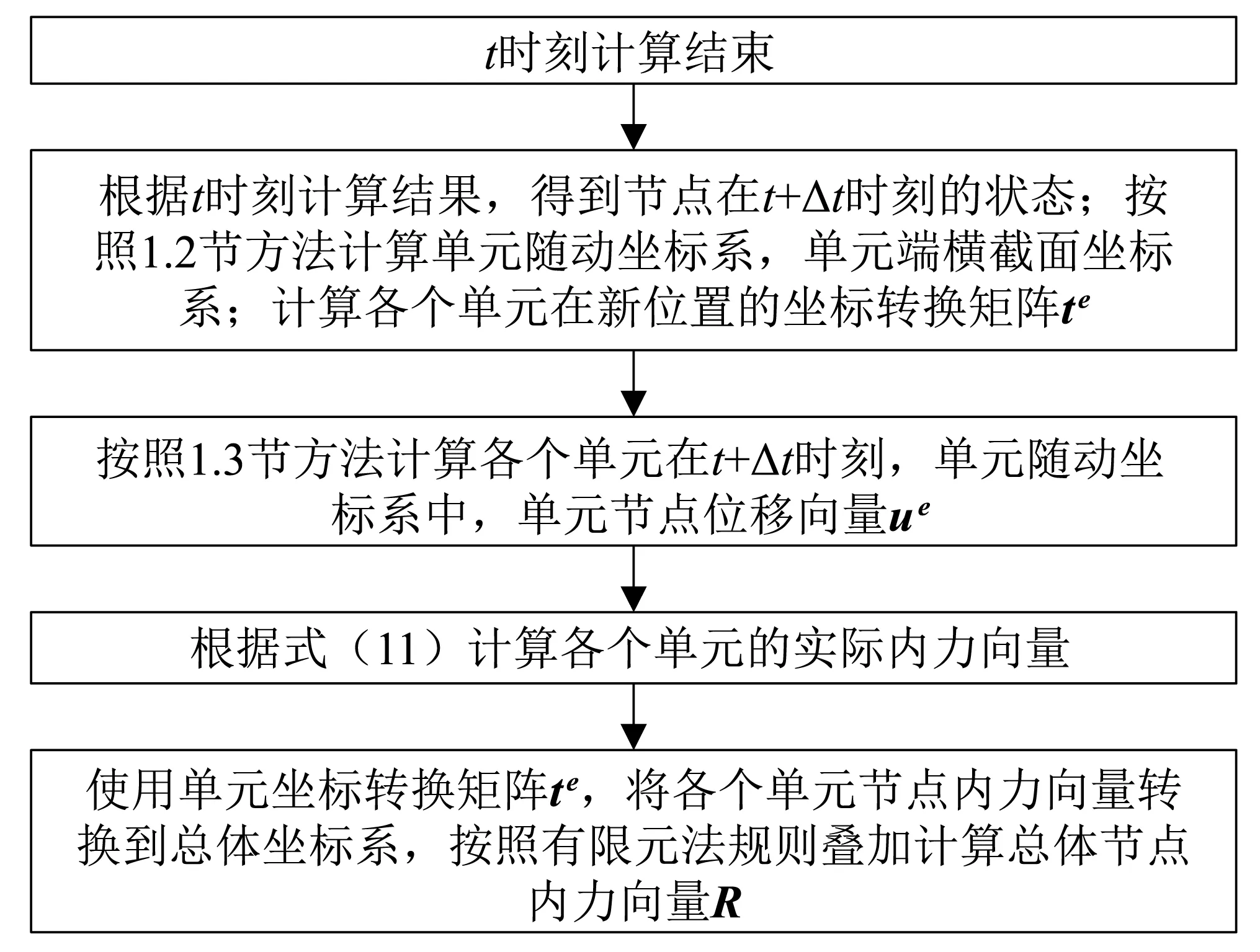
图4 有限元模型总体节点内力向量计算流程Fig.4 The calculation process of the global nodeinternal force vector of FEM modal
结构产生大变形时,有限元模型的总体节点外力向量可表示为F(u),也为位移的非线性函数。直接作用在节点上的外力在通常情况下可以认为其不变,如果发生改变也可以使用分级加载实现外力的变化。而重力加速度、单元初始应力的造成的等效外力,必然会随着结构的大变形而改变,因此本文计算中考虑了重力与单元初始应力的非线性时变效应。总体节点外力向量计算流程,如图5所示。

图5 有限元模型总体节点外力向量计算流程Fig.5 The calculation process of the global nodeexternal force vector of FEM modal
根据图4与图5的计算流程,可以看出,在CR列式算法中,结构在总体坐标系下,所有的几何非线性效应都是由位移造成的坐标转换矩阵的变化来反映的。由于CR列式为“几何精确方法”,所以从理论上来讲,荷载的分级加载的步数对最后结果无影响,差别主要来自于数值舍入的误差。
如果结构处于最终的静力平衡状态,有如下关系:
R(u)=F(u)
(12)
静力计算的最终目的就是得到结构在外力作用下达到静力平衡状态时总体坐标系下有限元模型各个节点的位移向量u。对于式(12)依据CR列式计算原理,一般使用Newton-Raphson迭代法计算,迭代中所需要的总体切线刚度矩阵可以通过叠加当前时间步中结构总体弹性刚度矩阵与应力刚度矩阵来得到。
2 基于CR列式的非线性有限元动力时程积分
2.1 基本理论
在3维杆、梁单元非线性静力计算的基础上,本文开发了基于CR列式的非线性Newmark-β有限元动力时程积分方法,在算法中也考虑了结构初始应力的影响。其基本假定与普通的Newmark-β法相同:
(13a)
(13b)

(14)
将式(13)代入式(14)可以得到:

(15)
这样,根据Newmark-β的基本原理,非线性有限元动力时程积分就被转化为在每一个时间步内求解非线性方程组(15)的问题,可以采用CR列式方法原理,使用Newton-Raphson法来进行平衡迭代计算。
式(15)左端中的总体节点内力向量R是总体节点位移向量u的非线性函数。对于R可以按照图 4中的流程来计算 。
在考虑结构几何非线性时,式(15)右端中,F表示结构承受的总体节点外力向量(如:重力、结构上施加的外力),Fe表示结构初始单元应力造成的等效总体节点外力向量(与ANSYS中初应变导致单元等效外力的概念相同,在本文有限元程序建模中可以直接定义单元初始轴力,拉力为正,压力为负)。F,Fe都是位移u的非线性函数,可以按照图5中的流程来计算。
式(15)左右两端还存在与总体质量矩阵M、总体阻尼矩阵C相关的等效力项。在非线性动力时程计算中,节点位置的变化必然会导致M的变化,所以在每一个时间步的计算中要根据当前节点位置使用坐标转换矩阵来更新M。由于阻尼的复杂性且在一般情况下结构阻尼的变化对振动的影响不大,在本文计算中不考虑C的改变。
使用Newton-Raphson迭代法求解式(15),当迭代未收敛时,式子左右两端是不相等的,计算两端的差值就可以得到迭代的不平衡力。在迭代过程中使用的切线刚度矩阵为Newmark-β法的等效总体刚度矩阵:
K=a0M+a1C+KK
(16)
式中:M,C,KK分别为将节点坐标更新到当前迭代步位置上时,结构的总体质量矩阵、总体阻尼矩阵、线性静力计算时计算的总体刚度矩阵。在本文计算中KK使用单元弹性刚度矩阵叠加单元应力刚度矩阵来组集。为了加快迭代计算收敛速度,式(16)也根据节点位置状态来更新。
2.2 算法流程
综上所述,基于CR列式的几何非线性Newmark-β有限元动力时程积分基本计算流程,如图6所示。
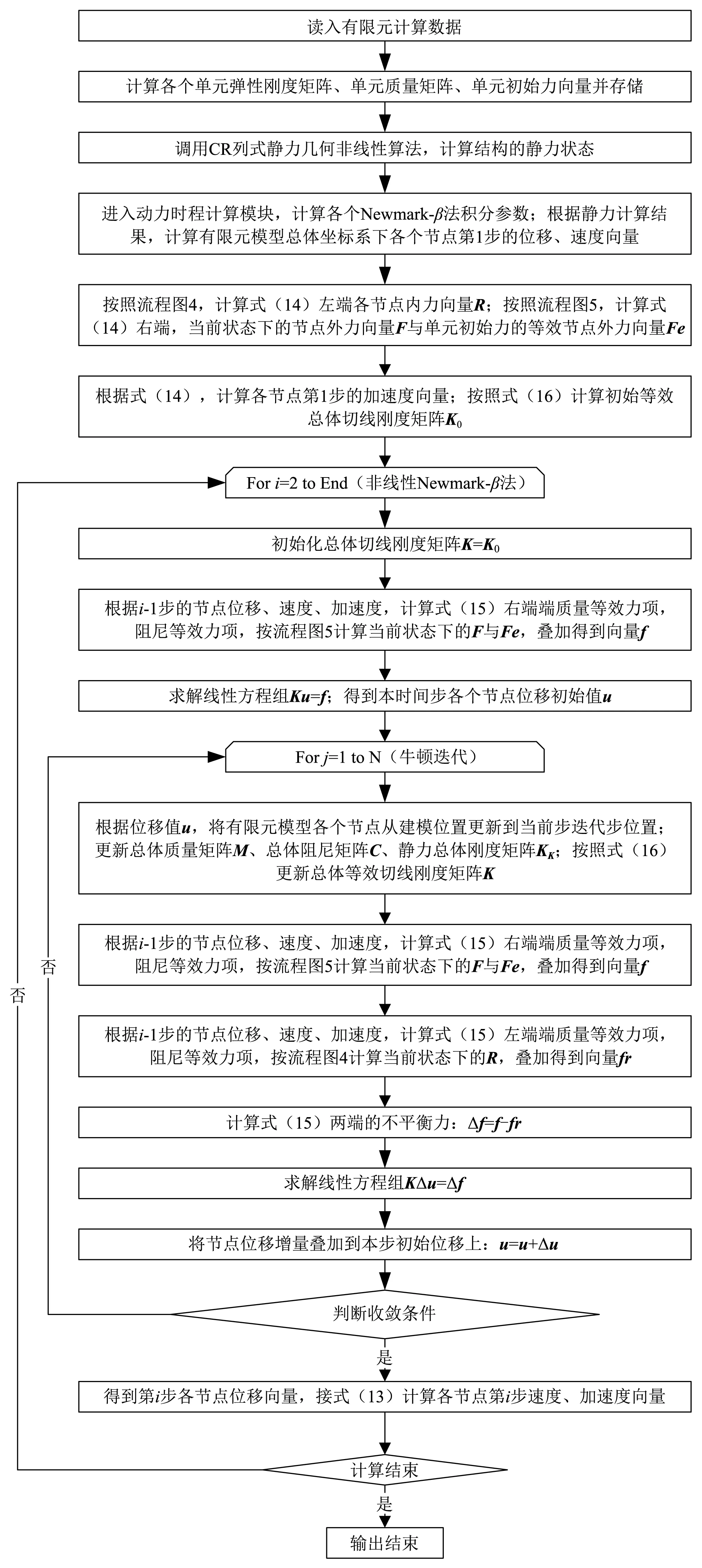
图6 非线性有限元动力时程计算流程图Fig.6 Calculation flow graph of nonlinear time-history FEM
3 算例验证
依据前文所述原理,使用MATLAB数值计算平台,本文开发了基于CR列式的3维空间结构非线性动力有限元程序,程序主要实现的功能如下:①可以考虑几何非线性计算结构静力状态;②可以在得到结构发生非线性大变形的静力状态后,计算结构的动力特性;③可以在计算中考虑初始应力与自重的时变效应,计算结构在外激励或强制位移激励作用下的非线性动力时程响应;④可以根据非线性动力时程计算结果绘制输出结构非线性振动的动画。
3.1 算例1 弯曲梁3维空间静力计算
本文中CR列式3维非线性动力时程计算是以非线性静力计算为基础的,所以,这里首先使用一个经典的静力模型来验证算法的正确性。
如图7所示,45°弯曲梁空间弯扭几何非线性大变形计算。与参考文献[9]中的结构相同,在XYZ坐标系中,梁的B端固结位于坐标系原点,A端不受约束且受到沿Y方向的力,梁共分为8个等长度的空间梁单元,各个节点坐标按照圆弧曲线计算。材料弹性模型为E=107,泊松比u=0,剪切模量G=E/2(1+u) ,圆弧半径R=100,截面尺寸为的矩形1.0×1.0。端点力P在计算迭代过程中始终保持沿Y方向。非线性静力计算中本文程序与ANSYS均设置12级分级加载。

图7 弯曲梁3维空间模型Fig.7 The mode of a curving beam in 3D space
图8中给出了P=300,P=600时,结构在静力作用下发生大幅度变形后的构型。
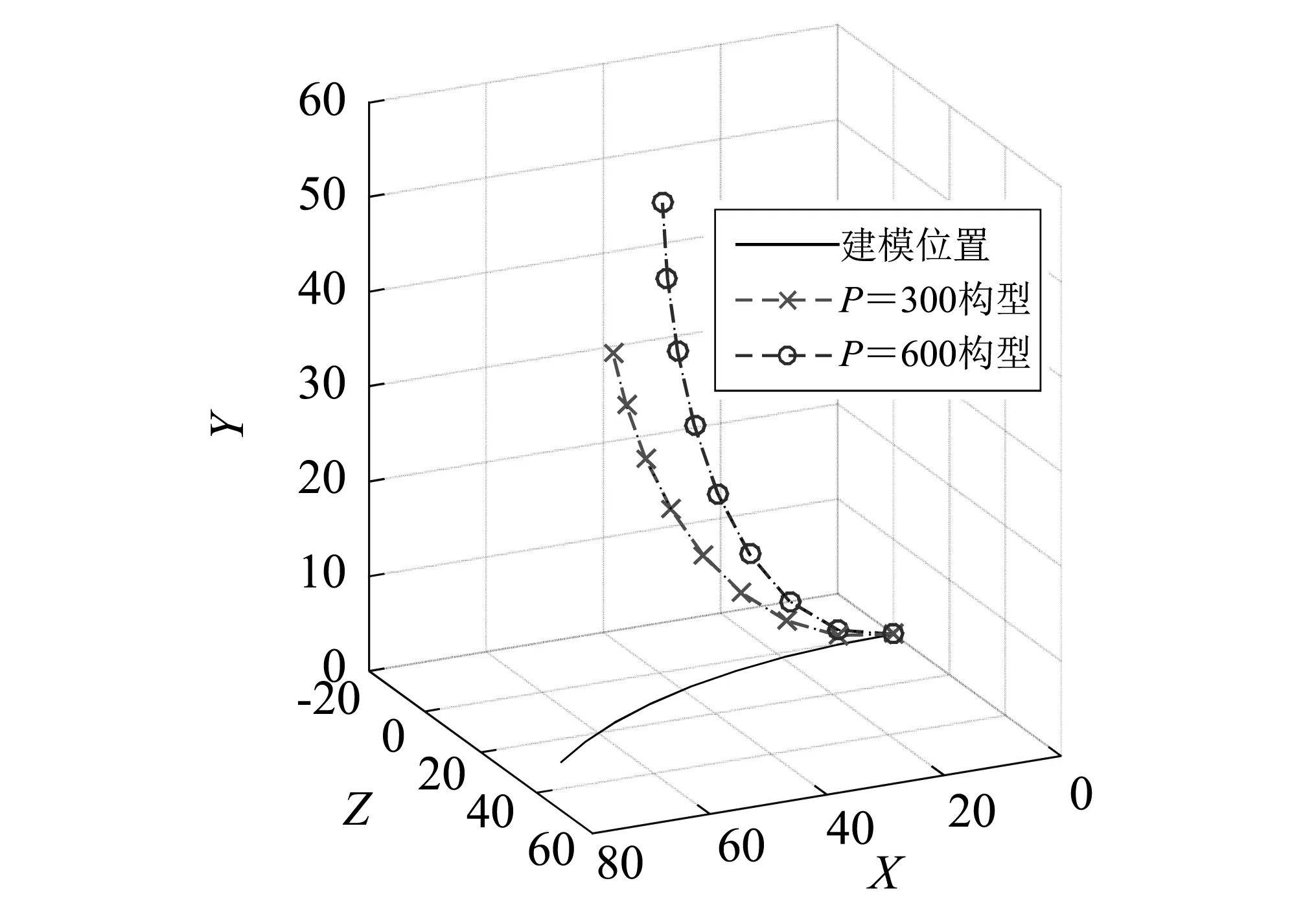
图8 弯曲梁3维空间变形Fig.8 The displacement of the curving beam in 3D space
已知弯曲梁在变形前,梁端节点A的位置坐标为x=70.7,y=0,z=29.3。使用本文程序计算得到结构变形后的坐标位置与参考文献[9]和ANSYS计算得到节点A的位置结果对比,如表1所示。

表1 计算结果对比
由表1可以看出,由于都采用基于CR列式的几何非线性静力计算方法,本文计算结果与参考文献差别很小,本文认为这是由于程序设计的细节差别造成的。由于结构的变形很大,且ANSYS中几何非线性计算使用的是UL列式,所以ANSYS结果与本文以及文献[9]的差别相对较明显一些。
3.2 算例2:索-梁组合结构3维空间非线性振动计算
桥梁工程中常见的索-梁组合结构简化模型[15],有限元模型的几何尺寸,如图9所示。
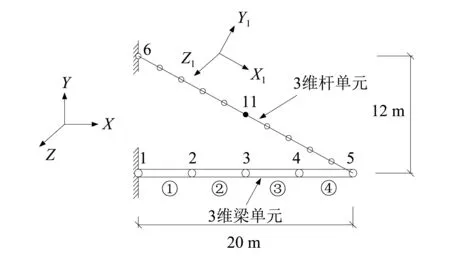
图9 索-梁组合结构有限元模型Fig.9 Cable-Beam structure FEM modal
总体坐标系为XYZ,建立拉索模型局部坐标系为X1Y1Z1,Z1与Z轴指向相同。梁分为4个3维梁单元,拉索共分为10个3维直杆单元。不计泊松比,结构单元的各个物理参数为:弹性模量E, Pa、剪切模量G, Pa、材料质量密度ρ, kg/m3、单元截面积A, m2、梁单元抗弯惯性矩Iz, m4,Iy, m4、抗扭惯性矩Ix, m4、杆单元初始轴力H, N,如表2所示。

表2 结构单元物理参数
为了验证本文程序的正确性与可靠性,通过算例的结果与ANSYS对比。ANSYS中使用Beam4梁单元模拟主梁,使用Link8杆单元模拟拉索,这两种单元的都为3维单元[16]。本文程序与ANSYS计算均使用一致质量矩阵。
程序计算中的重力加速度均取为G=9.8 m/s2。计算中不设置结构阻尼。由文献[16]可知ANSYS计算中默认的算法阻尼不为零,即:Newmark-β法中参数γ=0.505,在本文程序计算中使用相同的设置。
首先,使用本文有限元程序考虑几何非线性计算结构在自重作用下的静力构型,然后计算动力特性,在总体坐标系XYZ下得到前6阶模态计算结果,如图10所示。
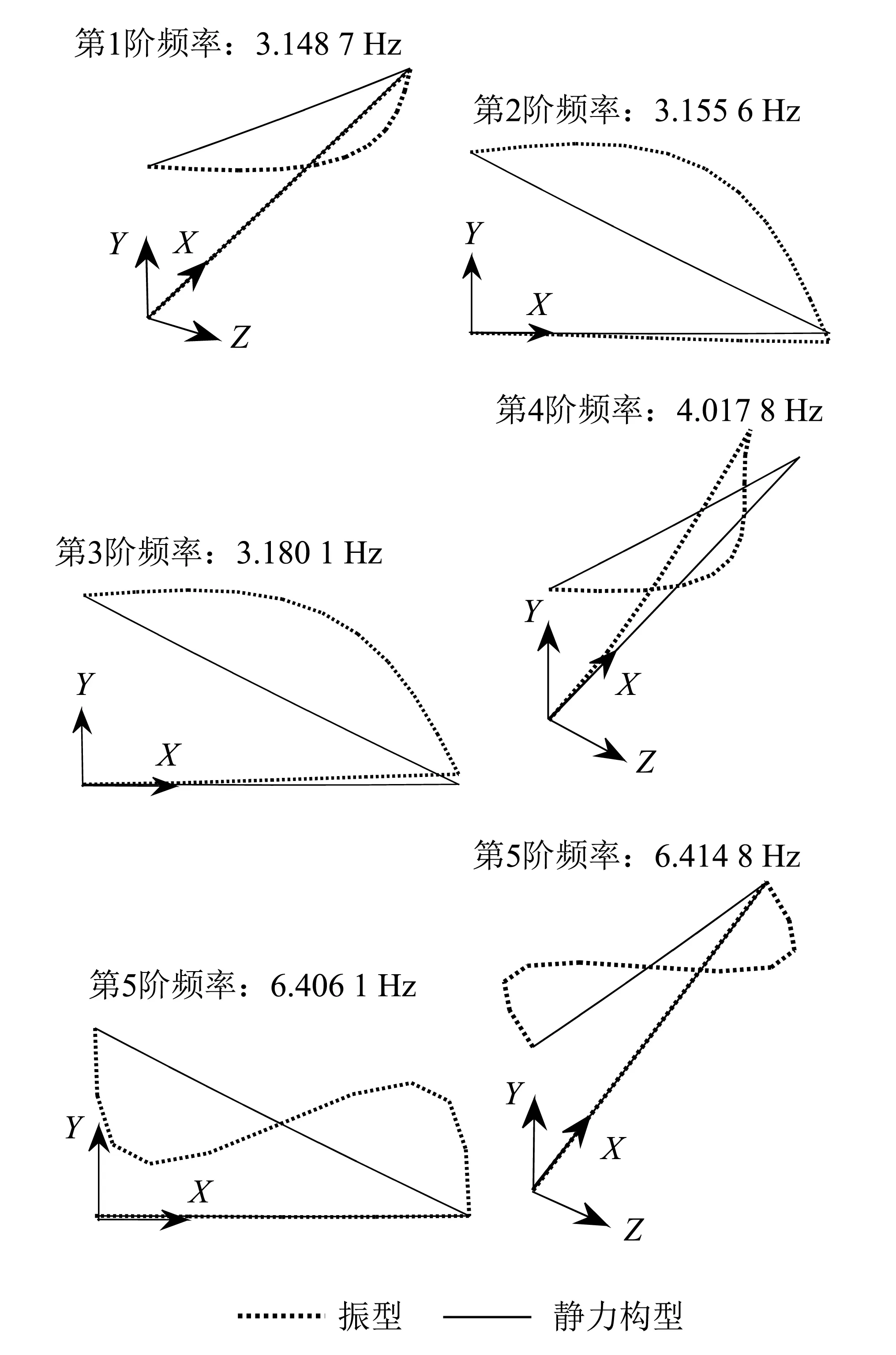
图10 结构前6阶模态Fig.10 The first six modes of the structure
非线性静力计算结果得到结构在自重下拉索的平均轴力(各单元轴力之和除以单元数量)为50.65 kN,根据文献[15]中的计算公式,单独计算拉索的自振频率,可以得到拉索在X1Y1平面内1阶自振频率为3.166 5 Hz,拉索在X1Z1平面内的1阶自振频率为3.153 9 Hz。
观察图10 (第2阶振型)可以看出,由于拉索局部的1阶自振频率接近整体结构的1阶自振频率,根据非线性振动理论, 整体结构发生1阶振动时,在端点位移激励(节点5)沿拉索局部坐标系Y1方向的分量作用下,拉索会发生1阶非线性1∶1主共振。
然后,在节点5上作用Y方向竖向力P=10 kN,静力计算后释放节点力,动力时程积分取时间步长为0.02 s,分别使用ANSYS与本文程序计算结构在平面内有自重状态下的振动时程,如图11所示。

图11 索-梁组合结构面内非线性振动ANSYS与本文程序计算结果Fig.11 The results of the Cable-Beam structure in-plane nonlinear vibration which calculated by ANSYS and the program of this thesis
从图11可看出,在释放节点力后结构发生了振动,拉索在梁的带动下发生了1∶1主共振,拉索端部(节点5)沿整体坐标系Y方向0.01 m幅值的位移激励,导致拉索中点(节点11)沿局部坐标系Y1方向发生了0.06 m的振动。结构振动体现了“拍振[17]”的非线性振动性质,振动能量在拉索与整体结构之间互相传递,呈现“此消彼长”的趋势。符合非线性振动的理论预期。
如图11所示,由于非线性动力时程计算中考虑了重力的直接作用,本文与文献[11]不同,本文计算结果中振动位移初始数值不为零,结构模型在自重作用下非线性静力计算后的初始位置(偏离y=0位置)为振动平衡位置。有限元模型主梁端部节点5在自重作用下的静力位移较小(约0.001 m),偏离较不明显,而拉索中点节点11(模型自重初始静力位移约为0.02 m)的振动时程图可清晰地看出这个计算结果。
在单元节点5上施加简谐力外激励P=P0sin(ωt),其中P0取为1.0 kN,ω对应的频率取为3.16 Hz。由于简谐力与结构面内的1阶自振频率接近,所以,在外激励作用下整体结构会发生共振,从而导致拉索发生1∶1主共振。得到拉索1/2点的沿局部坐标系Y1方向振动时程计算结果,如图12所示。

图12 索-梁组合结构在外激励作用下拉索1/2点的沿Y1方向振动时程图、频谱图Fig.12 The time-history curves and spectrogram of the 1/2 point of the cable nonlinear vibrationin Cable-Beam structure in Y1direction under external excitation
从图12中可以看出,结构在简谐激励下发生了共振,拉索振幅迅速增加(最大约0.3 m)但由于几何非线性的作用,拉索振幅不会持续增加,根据文献[17]的理论描述,这是由“振动硬化”现象导致的,即:几何非线性造成结构的振动频率随着振幅增大而增加。从计算结果频谱图中可以看出拉索的振动包含了比自振频率更高频的成分。同事,计算结果时程图中观察到了非线性振动造成拉索振幅随时间“涨落”的更为明显的“拍振”现象。
这里如果使用线性动力时程计算,由于结构刚度不变,在结构发生共振时,理论上振幅会持续增加,直致小阻尼限制的上限,会远大于非线性振动幅值上限,也不会发生非线性振动特有的振动硬化现象。所以,柔性结构的大幅振动必须考虑几何非线性效应。
对比图11与12中使用ANSYS与本文程序计算得到的振动时程图,二者在振动发展初期几乎是一致的,由于ANSYS非线性有限元计算使用的是更新拉格朗日格式(UL列式)与本文CR列式有一定的区别,所以,两者的计算结果存在细微差别,随着时间增加,动力时程积分的累加作用会导致差别相对小幅度增加。二者的时程计算结果都符合非线性振动的理论预期。因此,通过与ANSYS的对比验证,笔者认为本文程序的计算结果是正确、可靠的。
为了讨论索-梁组合结构的面外非线性振动,在图9模型节点5上,施加沿Z方向的横向力P=25 kN,静力计算后释放节点力,动力时程积分取时间步长为0.01 s,使用本文程序计算结构在有自重状态下的振动时程,得到梁上节点5与拉索1/2点(节点11)沿面外Z方向的振动时程,如图13所示。

图13 索-梁组合结构沿面外Z方向非线性振动时程图、频谱图Fig.13 The time-history curves and spectrograms of the cable-beam structure nonlinear vibration in out-plane Z direction

图14 索-梁组合结构非线性振动时程状态Fig.14 The time history states of nonlinearvibration of the cable-beam structure
同样观察图10(第1阶振型)可以知道,由于拉索的面外1阶自振频率与整体结构接近,拉索在梁的带动下发生了面外主共振(沿Z方向)拉索发生了相对较大幅度的振动。梁的面外抗弯刚度较大,所以“拍振”现象对梁的振幅涨落相对较不明显。由于振动硬化现象的作用,结构响应频率中(4.0 Hz)存在大于面外自振频率(3.148 Hz)的成分。
使用MATLAB可视化动画技术,我们可以更加直观地观察到结构在3维空间的非线性振动状态,但限于表达方式,本文这里仅根据计算结果列出结构发生面外振动(横向)在0~1.2 s内的非线性振动时程状态(振动位移放大5倍),如图14所示。
从图14中可以看出,由于非线性振动效应,计算结果中观察到了拉索的振动滞后现象,即:梁向左端振动、拉索向右端振动的状态(如第0.65 s)。这是更加符合实际情况的计算结果。
3.3 算例3:拉索3维空间回旋运动计算
如图 15所示,一根紧绷的水平布置拉索,AB两端固定,受到重力作用。在拉索端点A上作用圆弧型的位移激励,拉索发生空间运动。
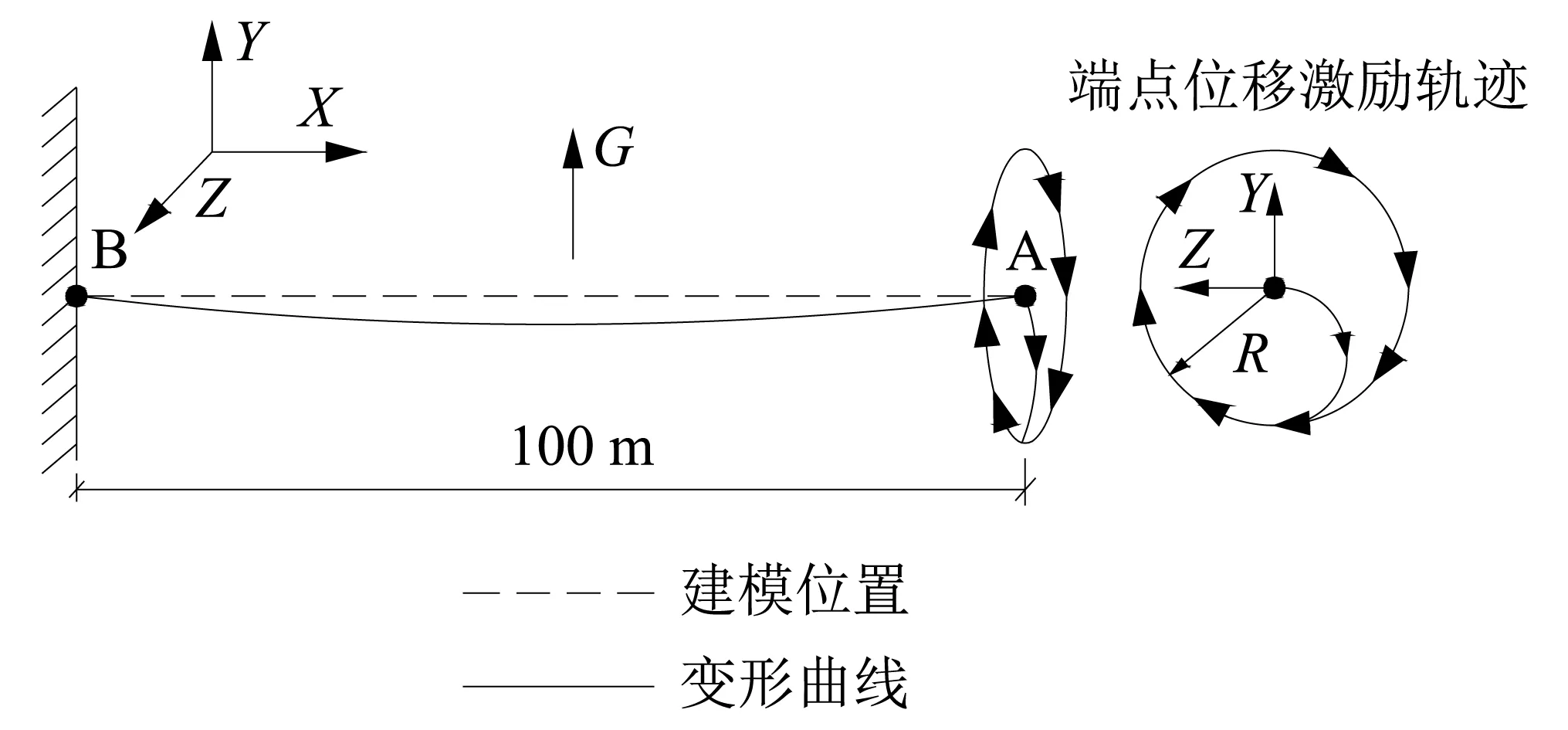
图15 拉索受端点位移激励示意图Fig.15 The schematic figure of the cablewith displacement stimulation at the end point
已知拉索两端的长度为l=100 m(建模长度),弹性模量E=2.01×1011Pa, 截面积A=0.08 m2,拉索的初始轴力为H=4 000 kN,重力加速度G=9.8 m/s2,拉索分为20个3维直杆单元。
设拉索AB端水平固定,考虑几何非线性,静力计算得到拉索的自重状态,垂度为-0.194 7 m,然后,计算自振频率得到拉索面内(XY平面)为1.257 7 Hz 面外自振频率(XZ平面)为1.252 8 Hz。
在得到拉索的自重状态后,在拉索端点施加圆弧轨迹位移激励,如图15所示,设端点A圆弧运动半径R=0.005 m,在ZY坐标系中Z方向分量为z=Rsin(ωt),Y方向运动分量为Rcos(ωt),设置拉索端点A圆弧运动频率为1.253 Hz,则ω=1.253×2×π=7.872 8 rad/s。
使用强制位移施加端点位移激励,取动力时程积分步长为0.02 s,计算2 000步。为了使“拍振”减小,振动尽快进入稳定状态,须设置较为明显的阻尼作用,不设置结构阻尼,设置算法阻尼γ=0.55。得到拉索中点在3维空间振动的运动轨迹曲线,如图16所示。

图16 拉索中点3维空间非线性振动曲线Fig.16 The nonlinear vibration curveof the 1/2 point of the cable in 3D space
从图16中可以看出,微小的端点位移激励,导致拉索发生较大幅度的空间振动,拉索中点的运动轨迹呈明显的圆曲线状态。
造成上述现象的原因为:由于拉索的索力较大,在自重作用下,拉索面外1阶自振频率仍然接近面内1阶自振频率,而拉索端点位移激励沿圆周运动且频率接近拉索的面内与面外1阶自振频率,因此,在端点位移激励下拉索发生了1阶面内-面外耦合的1∶1主共振,导致了较大幅度的3空间回旋运动,即:柔性索的“跳绳”运动现象。
4 结 语
(1)开发了3维空间杆梁单元基于CR列式的非线性Newmark-β动力时程有限元算法,阐述了程序计算原理,编制有限元计算程序,通过算例与ANSYS计算结果对比,验证了程序的正确性与可靠性。
(2)基于本文算法开发的有限元程序具有通用性,可以计算杆梁结构在3维空间中外力作用下的非线性振动,也可以计算结构在强制位移激励下的非线性振动,可以在动力时程计算中考虑初始应力与重力随结构大幅振动的时变效应。
(3)经过算例验证表明,本文的CR列式非线性动力时程算法具有简洁、可靠、高效的特点。在笔者计算机上,采用同样的计算设置,使用ANSYS进行非线性动力时程计算,算例1耗时约为3s,算例2约为150 s,算例3约为120 s,而使用本文程序耗时分别约为1 s、30 s、23 s。
(4)非线性有限元动力时程计算能更好地反映结构的受力细节,为柔性结构的非线性振动研究提供了较为完善的解决方案。对于桥梁工程专业,自主开发计算程序更有利于整合本专业的各个算法,如:风-车-桥耦合振动算法。计划在后续的研究中完善本程序,优化计算效率,进一步提高非线性动力时程积分的计算速度并将其运用到实际大跨度斜拉桥、悬索桥3维空间全桥模型非线性振动的计算分析中。

