区域电离层估计方法在网络RTK中的应用

张晋升，李成钢，2，何 冰，袁志敏

(1.广州市中海达测绘仪器有限公司，广州 510000；2.中山大学 地理科学与规划学院，广州 510000)

0 引言

北斗卫星导航系统(BeiDou navigation satellite system，BDS)已经广泛地应用到生产实践中，连续运行参考站系统(continuously operating reference stations，CORS)[1]是实现中长距离高精度实时动态定位的有效手段，网络实时动态差分法(real-time kinematic，RTK)在中长距离厘米级实时动态定位领域仍是主流模式[2-3]。电离层延迟误差在时间和空间上存在着较大的无序性和复杂的变化趋势，是影响移动用户(尤其是单频用户)定位精度和可靠性最主要的因素[4]。目前在CORS系统中通常采用三步法固定基准站模糊度，再根据模糊度反算电离层延迟，从而进行误差建模。由于三步法中固定宽巷模糊度时用到了伪距观测值，在使用非进口主板或者伪距粗差较多时，基准站模糊度固定率显著下降。

本文基于载波相位观测值，建立区域电离层误差模型，并把电离层模型系数和模糊度参数一并进行卡尔曼滤波估计，消除伪距粗差的影响，以期提高电离层参数估计精度和基准站网解模糊度固定成功率。

1 常规电离层延迟计算方法

1.1 经典电离层模型

经典电离层改正模型主要有：本特(Bent)模型、国际参考电离层(international reference ionosphere，IRI)模型、克罗布歇模型(Klobuchar)[5]。这些电离层模型都是一些反映在正常情况下的理想电离层状况的经验公式。利用它们来计算某一时刻、某一地点的电离层的精度都不够理想，其误差可达20 %～40 %，甚至更大[6]。

全球电离层图(global ionosphere maps，GIM)是以IONEX(ionosphere map exchange format)格式给出的国际全球卫星导航系统(global navigation satellite system，GNSS)服务组织(International GNSS Service，IGS)的电离层产品，是IGS数据处理中心每天利用全球大约200个跟踪站的观测资料计算得到的全球电离层产品，以文本格式给出，也可格网化生成全球电离层图。按1组/(2 h)提供全天24 h的全球电离层图[7]。

由于伪距观测值的噪声较大，可以采用载波平滑伪距计算电离层[8-10]。

1.2 三步法

采用载波相位观测值计算电离层是目前CORS系统的主流方法，主要过程分3个步骤[11]：

1)利用MW(Melbourne-Wubbena)组合时间序列均值计算宽巷模糊度[12]；

2)采用消电离层组合的方法构建法方程并滤波解算出消电离层组合模糊度；

3)根据第一步和第二步的结果，滤波解算窄巷模糊度。

在固定L1和L2频率的整周模糊度之后，电离层延迟的计算公式为

(1)

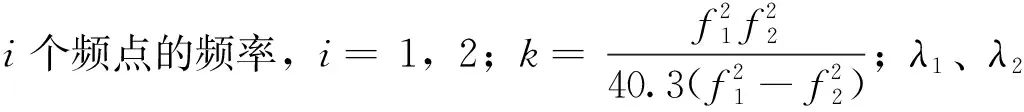
2 区域电离层模型参数估计理论与流程

2.1 载波线性组合观测值模型

目前全球定位系统(global positioning system，GPS)、格洛纳斯系统(global navigation satellite system，GLONASS)、BDS都有2个频率的观测值，因此可以把不同频率之间的观测值进行线性组合，从而获取一种更加有利于特定的参数估计组合。本文采用宽巷观测值的线性组合方法，公式为

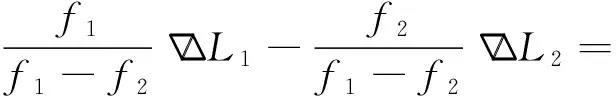
(2)

其中由于GLONASS系统每颗卫星的波长不同，其双差模糊度计算方法与GPS、BDS略有不同，双差宽巷模糊度为

(3)

2.2 电离层区域模型建立

电离层单层模型的高度通常定为350 km，卫星轨道高度约为20 000 km，如图1所示为测站在电离层穿刺点所在的曲面即中心电离层面的投影示意图。A，B站点的电离层穿刺点分别为a1、a2、a3和b1、b2、b3，根据电离层高度和卫星轨道高度的比例关系，可以认为a1、a2、a3相互独立，b1，b2，b3相互独立，而ai，bi(i=1，2，3)分别相关。

图1 参考站在电离层穿刺点处的投影

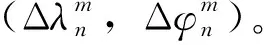
(4)

式中：Δλ、Δφ分别为当前测站与中心点的经度、纬度差值；I(Δλ，Δφ)为当前站点的电离层值；M(Δλ，Δφ)为电离层穿刺点的映射函数；an，m为模型系数；n、m分别表示测站数目和卫星数目。通常只需展开到一阶项，即

(5)

2.3 电离层参数滤波模型的建立与解算

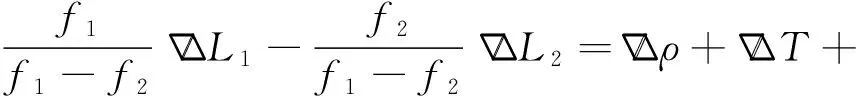
(6)

假设在某一观测历元t，该区域内的N个基站共观测到了S颗卫星，则误差方程的形式为

V=AX-L

(7)

式中：A为系数；X为参数；L为常数项；V为观测值残差。以3个基站A、B、C组成1个三角形网为例，公式为

(8)

式中AAB，ABC，ACA分别对应3条基线观测方程的系数矩阵。它们的形式类似，以其中一条基线的系数矩阵为例，包含对流层参数系数、电离层参数系数、宽巷模糊参数系数，其具体形式为

(9)

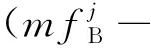
参数为

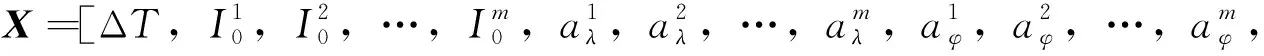
(10)

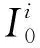
L是观测值减模型值，具体表达形式为

(11)

通过组建观测方程，并把表征电离层延迟的3个参数和对流层参数、模糊度参数一并估计，可实时获取测站区域电离层延迟信息。采用Kalman滤波模型，实时更新电离层、对流层参数，需要注意电离层具有区域性和根据当地时变化的特性，即不同区域的电离层处理噪声有差别。考虑到电离层误差延迟的时变特性，在Kalman滤波的处理噪声矩中体现电离层参数的方差特性，可根据区域和时段给定合适的处理噪声，如(10-4m/s)×(10-4m/s)。

3 实验与结果分析

3.1 数据来源

为了验证该方法的可行性和电离层精度，作者采用了CORS基准站网的实时数据流进行实验。实验场地是某市CORS地基增强系统。GNSS天线采用3D扼流圈天线，通过美国国家大地测量局(National Geodetic Survey，NGS)认证，天线相位中心稳定性优于1 mm，相位中心偏移量为0.8 mm；基准站接收机可以同时接收GPS、GLONASS、BDS、Galileo以及星基增强系统(satellite-based augmentation system，SBAS)全星座的数据，数据可用率高于99 %。

3.2 实验方法

考虑到网络RTK需要的电离层延迟精度要优于3 cm，此次实验的结果只和MW方法进行对比，不再与常规电离层方法作对比分析。

实验中采用了景谷(JIGU)、碧安(BIAN)、因远(YIYU)、文武(WEWU)、通关(TGUA)5个站进行区域电离层建模分析，滤波解算出电离层系数，再根据模型系数计算出TGUA-NIER基线的双差电离层延迟信息即模型值。采用事后计算的方法得到TGUA-NIER基线的双差电离层延迟信息作为真值，并与模型值进行对比分析，检验本文采用的电离层区域模型的精度和可靠性。

3.3 实验结果

1)双差电离层延迟估计精度分析：

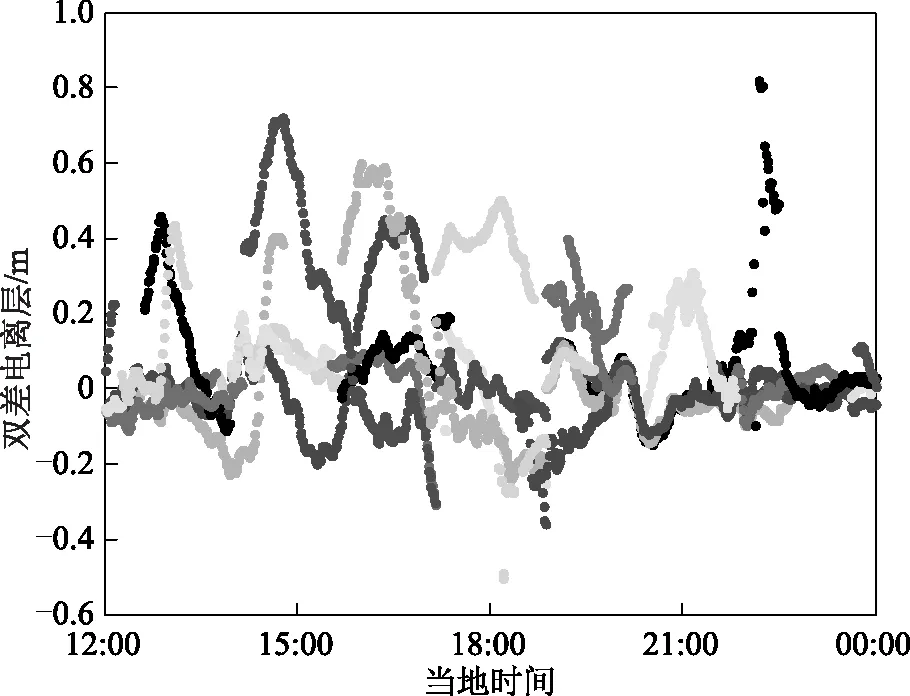
图2 双差电离层真值

①真值采用TGUA-NIER站基线数据事后解算结果，如图2所示，图中坐标横轴表示当地时间，坐标纵轴表示双差电离层，单位为m，不同颜色表示不同的卫星，图中给出了该时段所有观测到的卫星。可看出电离层在下午时段非常活跃，双差电离层达到0.7 m。图3给出了该时段所有卫星的高度角信息，图中坐标横轴表示当地时间，坐标纵轴表示卫星高度角。

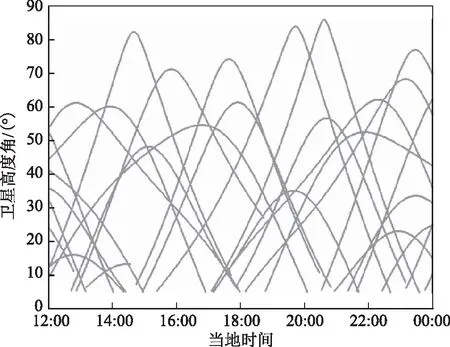
图3 卫星高度角

②MW方法：利用MW组合方法计算宽巷模糊度，再根据消电离层组合计算窄巷模糊度，从而得到2个频率的模糊度，根据公式计算得到双差电离层。该方法是目前CORS系统主流方法，由于在计算宽巷时依赖于伪距质量，出错几率较大，如图4所示，阴影表示计算出错的时刻。

图4 MW方法计算出的双差电离层值

③电离层区域模型参数估计方法：采用载波相位观测值，观测值精度高，结果更加稳定，如图5所示。该方法需提供双差电离层参数初始值约束信息(初始值约束信息计算在下文说明)，如果该约束信息误差太大，会导致方程收敛时间较长。

图5 参数估计法计算出的双差电离层值

2种方法计算的电离层延迟与真值比较的残差信息如表1所示，可知参数估计法的稳定性要更高。

2)模糊度固定率改善分析

①MW方法依赖于伪距质量，基线总体固定率较低，有时会出现长时间的系统偏差，如图6所示。

表1 电离层残差统计 m

图6 MW方法计算的模糊度出现系统偏差

图中坐标横轴表示当地时间，坐标纵轴表示宽巷模糊度，模糊度的浮点解出现了0.4个周期的偏差，且长时间不能收敛到整数，从左至右分别是GPS 01卫星(参考星为GPS 21)、GLONASS 18卫星(参考星为GLONASS 03)、BDS 09卫星(参考星为BDS 03)。

②为了验证电离层区域模型方法的效果，采用2016-01-01—2016-01-31连续1个月的数据，限于篇幅，表2所示仅为2016-01-01—2016-01-07基线模糊度固定率(每天固定卫星个数大于16颗的时间百分比)结果。从表2中可以看出采用电离层区域模型参数估计法的基线模糊度固定率更加稳定，三星系统(GPS、GLONASS、BDS)固定卫星数大于16颗的时段超过了95 %。有效提升了地基增强系统基线解算的正确性和稳定性。

表2 模糊度固定率对比统计结果

3)网络RTK定位精度分析

图7 基于CORS网络的连续24 h静态RTK定位残差序列

为了测试电离层区域模型用于CORS系统之后对RTK定位效果的影响，分别进行了静态连续24 h的RTK测试和跑车动态RTK测试，结果如图7和图8所示，图中坐标横轴表示当地时间，坐标纵轴表示坐标残差，单位m。在静态模式下(图7)RTK定位残差标准差分别是N方向1.1，E方向0.9，U方向2.2 cm；在动态跑车的测试中，除去过隧道的时间，其他时段全部能得到固定解，为了验证动态测试的精度，在园区道路规则骑行一段距离，结果如图8所示，可以看出定位结果的准确性。

图8 基于CORS网络的跑车动态RTK定位效果

4 结束语

电离层延迟是影响定位精度最重要的因素，其变化具有较强的地域性和时域性。本文采用电离层区域模型参数估计的方法，采用载波相位观测值联立观测值信息进行滤波解算，实时获取高精度的电离层延迟信息。从电离层延迟估计精度、模糊度固定率改进分析、网络RTK定位精度分析3个方面的实验结果进行分析，得到以下结论：

1)通过区域电离层参数估计的方法比常规方法计算的结果精度更高，且更加稳定，不会受到伪距粗差的影响，模型值与真值的残差标准差优于8 mm；

2)采用区域电离层估计方法有助于CORS基线模糊度固定，通过连续1个月的数据解算结果可得，三星系统基线网模糊度固定卫星数超过16颗的时段超过95 %；

3)采用区域电离层估计方法可以为网络RTK用户提供准确稳定的差分改正信息，24 h静态测试和动态跑车测试可以看出，外业RTK时间可用率远远超过CORS系统要求的95 %的指标，定位精度水平优于2，高程优于3 cm。

然而该方法需要电离层先验值的约束信息，在使用的时候可通过事后处理多天的数据获取该区域的电离层24 h先验值。在CORS系统中，由于基准站连续运行，因此该问题可以较为方便地解决。