测站点近似坐标精度对GNSS测站解算的影响分析

刘洋洋，党亚民，许长辉

(中国测绘科学研究院 大地测量与地球动力学研究所，北京 100830)

0 引言

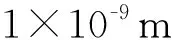
当前，国内外学者对影响GAMIT软件基线解算精度的各因素进行了研究。文献[4]利用间隔3 m的测站形成短基线，据此对不同短基线模型进行分析；文献[5]研究分析了星历误差对基线解算的影响；文献[6]分析了在GAMIT基线解算过程中不同参数的设置对基线解算精度的影响；文献[7]基于GAMIT分析了分段线性法中参数估计的时间间隔对高精度GPS数据处理精度的影响。但是关于近似坐标对观测数据解算的影响仍没有合适的研究，以GAMIT软件为例，该近似坐标文件名为“lfile.”，生成方式大致有3种：直接提取观测文件中位置信息、伪距单点定位获取、双差定位获取。

本文采用中国大陆周边的国际GPS服务(International GPS Service，IGS)站，利用GAMIT/GLOBK进行解算处理，将标准化均方根残差(normalized root mean square，NRMS)作为评估精度的主要指标，顾及基线长度对解算精度进行分析，并在同一坐标框架下分析不同的坐标偏差。

1 处理前预分析

1.1 GAMIT/GLOBK软件模块计算流程

GAMIT的解算模块主要有7个独立但衔接的程序：轨道积分模块、组成观测方程模块、单差自动修复周跳模块、双差自动修复周跳模块、人工交互式修复周跳模块、创建最终解算M文件模块和利用双差观测值根据最小二乘法求解参数最终解算步骤，各模块的解算步骤程序命令行如图1所示。目前应用的GPS接收机的性能较以前有了很大提升，在解决周跳问题中，不必使用人工修复，仅需要重复使用SINCLN或DBCLN模块即可[8]。

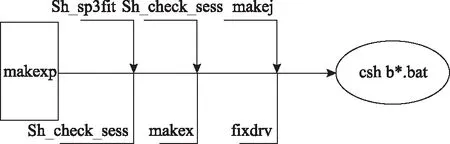
图1 GAMIT软件的数据处理流程

GLOBK软件本质是卡尔曼滤波器，软件利用观测向量估计随时间变化的状态向量，通过综合处理空间测量和大地测量数据，得到在同一框架下的结果及速度场，输入经过GAMIT处理后的hfile、-o、-q等文件，输出测站坐标等参数[9]。其计算流程框架如图2所示。

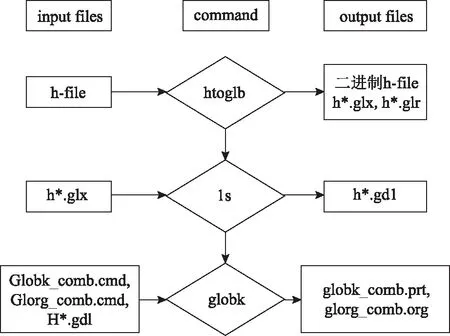
图2 GLOBKT软件计算流程

1.2 近似坐标的理论精度影响

GPS定位的实质原理是空间后方交会，由至少4颗卫星与观测站建立的站星距观测方程通过初始的测站坐标反复迭代，并通过多颗卫星得到最优的观测点最小二乘解。通过对观测方程的测站坐标分析来发现初始坐标精度对解算带来的影响，以伪距单点定位为例，将各种效应误差化为等效距离误差，站星距的观测方程为

(1)

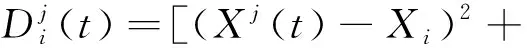
(Yj(t)-Yi)2+(Zj(t)-Zi)2]1/2

(2)

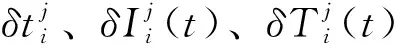
(3)

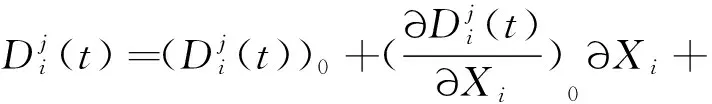
(4)

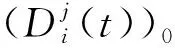
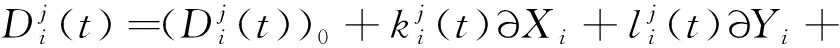
(5)

(6)

(7)

(8)

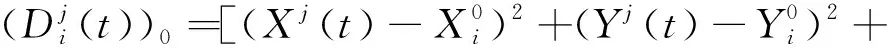
(9)

最终得到跟测站点近似坐标有直接关系的线性观测方程为

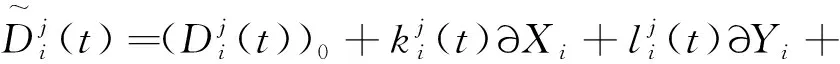
(10)

由式(1)～(10)可知，在基线解算时，测站点近似坐标精度在解算过程中，对迭代次数及最终解算精度方面有影响，由上式更可以直观的看出，测站点近似坐标精度与迭代次数成反比，与最终解算精度成正比。但是在实际解算中，需要顾及基线长度和解算时间等需求，如何根据不同的情况确定最优的解算方案，是值得具体探讨的。

2 实验与结果分析

由于需要分析坐标精度的影响，所选参考站需稳定，观测文件质量需较好，故选取2017年1月IGS站中中国区域及周边的23个站(BJFS、BJNM、CHAN、SHAO、TCMS、TWTF、TNML、ULAB、URUM、LHZA、BADG、TASH、POL2、CHUM、OSN4、SUWN、DAEJ、AIRA、GMSD、USUD、MIZU、TSKB、KSMV)进行处理分析，图3为测站点分布图。为了比较近似坐标精度对解算的影响，将BJFS、TWTF、URUM站设置为控制站，其他站设置为非固定站，设置该3站地心纬度、经度松弛量为0.05 m，设置矢径R松弛量为0.10 m，坐标约束设置为0.50、0.50、0.50 m；采用IGS提供的最终精密星历，基线处理类型设置为松弛型，使用无电离层的线性组合的观测值类型，设置VMF1的对流层映射函数模型以估计对流层延迟参数，采用ITRF2008参考框架在2017年1月的历元时刻的坐标，使用J2000空间惯性参考系。基于GAMIT软件分析以下3种形成“lfile.”文件的方式对GPS数据解算的影响：

1)直接提取观测文件中的近似坐标以形成近似坐标文件。

2)利用GAMIT中的svpos和svdiff模块进行单点定位生成站坐标，形成近似坐标文件。

3)利用GAMIT中的svpos和svdiff模块，将BJFS、TWTF、URUM的ITRF2008框架中的坐标作为基准，进行双差定位得到其他站坐标，形成近似坐标文件。

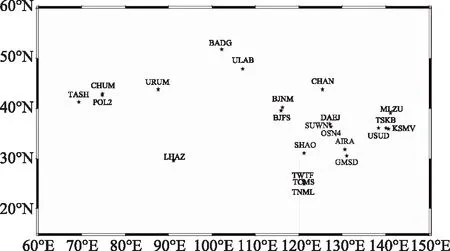
图3 所选取IGS站的分布

2.1 基线解算结果分析

NRMS表示解算出的单时段基线值与其加权平均值的偏离程度，是衡量GAMIT基线解算质量的1个重要指标，计算公式为

(11)

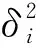
一般认为NRMS值应小于0.3，理想应小于0.25，则认为解算成功，否则需要检查原因，重新处理。若是NRMS值大于0.5，表明基线解算是有问题的，可能存在有未除去大周跳、某解算参数有问题、解算模型设定有误等情况。NRMS值越小，则代表基线解算的精度越高[11](如表1所示)。

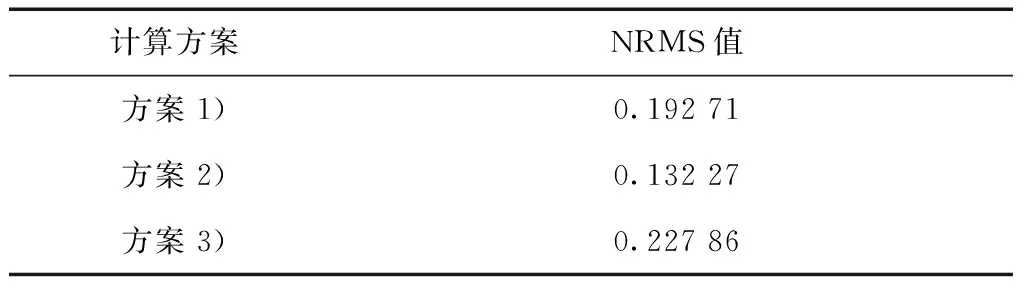
表1 各方案解算NRMS值

由表可以看出，3种模式解算的NRMS的值均低于0.25，符合解算要求；而其中方案2)，即进行单点定位形成近似坐标文件的处理策略的解算效果较其他2种更优，同时通过双差定位得到的NRMS结果值最大。

为了分析对基线长度的解算误差，选取了解算组合的所有基线进行统计分析，以基线长度为横轴，基线解算出的关于长度的中误差作为纵轴，统计结果如图4所示。

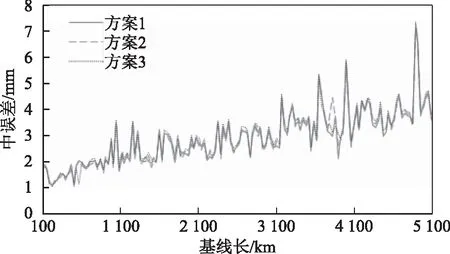
图4 不同方案解算的基线长误差

从图4可以看出：3个解算方案对基线长度的影响大体上趋势一致，并未因为不同方案而有较大差别，均值相互存在0.1～0.2 mm的差别，但是相对精度均达到1×10-9～1×10-10；3个方案统一表示出来，随着基线的长度增加，基线长度的中误差值随之增大，说明解算的基线误差跟测站距离有关，由此可见不同方案形成的lfile文件对基线长度的解算结果几乎不具有影响。综合表1和图4的结果可知：仅从解算时间角度考虑，方案2)和方案3)需要单独进行模块的定位以得到近似坐标，方案1)最为快捷简单；虽方案2)的NRMS值最好，但是方案1)的NRMS值也能较好地满足要求；所以如果解算要求最高精度，而不怕时间损耗，则选择方案2)，如要较快捷地得到精度合理的结果，则选取方案1)。

2.2 平差结果分析

将3种方案解算的基线结果文件采用GLOBK软件进行平差处理，将BJFS、TWTF、URUM 3站作平差起算站，采用ITRF2008框架在2017年年积日为第1天00：00：00时刻历元的坐标，得出3种方案在同一框架下的坐标，并提取出该历元时刻的ITRF坐标当作真值，分别将不同方案得出的坐标值与ITRF值作差并取绝对值，以此来比较3种方案坐标解算的精度，以下列9站的X、Z值为例，图5为对比结果。

由图5可以看出：在水平的X方向，方案2)的差值最大，与基线结果中该方案的NRMS值最小成反比，方案1)、方案3)的坐标值近似，并且由于方案3)双差定位中将BJFS、BJNM、TWTF作为参考站，所以在最终结果中，方案3)的该3点坐标精度最好，而方案1)总体较好，与ITRF坐标差值几乎都在2 mm以下；垂直Z方向，总体方案2)较好，恰恰与X值相反，却跟方案2)的NRMS值最小相对应，而方案3)的Z值精度最低，但是在所有的站中却不稳定，最大和最小相差10 mm，且作为起算站的TWTF站精度最差，也间接反映了该方案的不稳定性。因此综合比较X、Z精度差值可知，方案1)总体更稳定，精度也合适，没有出现较大起伏，加上考虑在基线解算时的时间因素，在应用GAMIT解算数据时，推荐采用方案1)，即直接提取观测文件中的近似坐标。

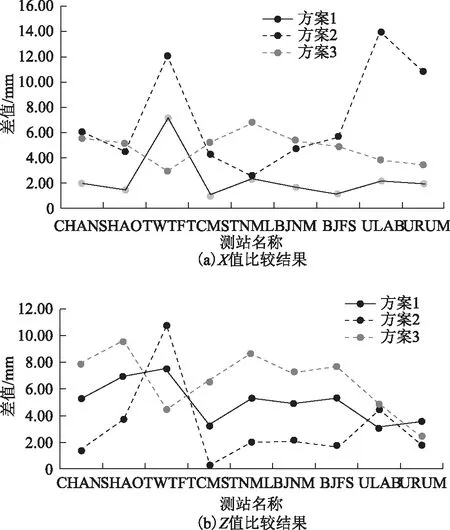
图5 坐标解算值与真值比较结果统计

3 结束语

文章采用了中国区域周边的IGS站数据，对生成坐标近似文件的不同方法进行了基线解算和平差处理，从NRMS值、基线精度和平差坐标差值等方面进行了对比分析，并考虑了处理过程中的时间因素，结果表明：

1)在利用GAMIT进行数据处理时，近似坐标文件的精度不同，不会造成解算结果文件的较大差异，都在合理范围内；并且并非利用双差定位得到的近似坐标参与解算的效果就一定最好，而是在大区域工程中，利用单点定位得到的基线解NRMS值效果最好，而小区域下，仍需做进一步的探索。

2)基线解算结果和坐标偏差在Z方向都是最大的误差因素，即使在水平方向误差最小的基线中，其Z方向误差也偏大，说明在数据解算的研究中应当着重于改善Z方向的误差。

3)如考虑解算的时间因素，既满足精度要求，也方便快捷，应当直接利用观测文件中测站的概略位置，而GAMIT10.6之后的版本可以直接通过设置配置文件来达到该目的。