BDS三频约束的多系统短基线模糊度单历元固定算法

刘 扬，余学祥，王胜利，柴大帅

(1.安徽理工大学 测绘学院，安徽 淮南 232001；2.山东科技大学 海洋工程研究院，山东 青岛 266590；3.中国矿业大学 环境与测绘学院，江苏 徐州 221116)

0 引言

随着全球卫星导航系统(global navigation satellite system，GNSS)的不断发展，美国的全球定位系统(global positioning system，GPS)和俄罗斯的格洛纳斯(global navigation satellite system，GLONASS)已经发展得比较成熟，而我国北斗卫星导航系统(BeiDou navigation satellite system，BDS)发展迅速，目前已完全覆盖亚太地区[1]，并计划2017年下半年发射BDS第三代卫星，将于2020年覆盖全球并实现服务；因此多系统之间的融合是未来发展的趋势。利用GNSS载波差分获得的厘米级高精度定位结果已经广泛应用于军事和民用领域，而载波差分定位的关键在于模糊度的快速固定，如何快速固定模糊度一直以来是国内外研究的热点和难点[2-3]。文献[4]提出利用多系统融合不仅能够增加观测卫星的个数、优化定位的几何结构，而且能够较好地解决信号遮挡等问题，大大地提高定位的精度和可靠性；并指出与只使用GPS单系统相比，解算时间大约减少了70 %，精度提高了25 %。

三频载波模糊度解算(three-carrier ambiguity resolution，TCAR)[5]和级联整数解算(cascading integer resolution，CIR)[6]都是比较经典的解算短基线模糊度的三频模糊度解算方法，二者的原理相似，采用无几何模型分别对超宽巷(extra wide lane，EXL)、宽巷(wide lane，WL)和窄巷(narrow lane，NL)的模糊度进行解算。基于上述理论，国内外大量学者对2种方法和改进的算法进行了研究，其中文献[7]使用TCAR，分别利用几何模型(geometry-based，GB)和无几何模型(geometry-free，GF)对模糊度进行固定；文献[8]在传统的TCAR的基础上引入电离层延迟先验信息，把电离层延迟、模糊度和位置参数作为未知数；文献[9]充分利用整数最小二乘法(integer least-squares，ILS)和CIR的优势提出了一种改进的载波相位模糊度固定方法。上述研究都利用了GNSS多频多系统的优势来进行模糊度固定，主要集中在多系统的组合方面，并未充分发挥单个系统在算法中的优势。

本文基于已有的三频模糊度解算方法，提出一种基于BDS三频约束的GNSS短基线单历元模糊度解算方法，以期快速可靠地固定GNSS差分模糊度。

1 模糊度固定算法模型

根据三频模糊度比较容易固定的特点，利用BDS三频载波观测值组合出多种不同波长的超宽巷和宽巷组合观测值来进行模糊度的快速固定[10]。首先快速求出超宽巷(0，-1，1)和(1，4，-5)组合观测值模糊度；然后根据线性关系求出(1，-1，0)组合的宽巷观测值模糊度，利用宽巷观测方程与B1载波观测方程组成无几何模型方程求出B1频点的模糊度；最后利用已固定的BDS B1模糊度来求算GNSS L1频点的模糊度。算法流程如图1所示。

图1 单历元GNSS模糊度固定流程

1.1 BDS三频模糊度固定算法

顾及对流层延迟和电离层延迟误差，伪距和载波差分观测方程[11]为

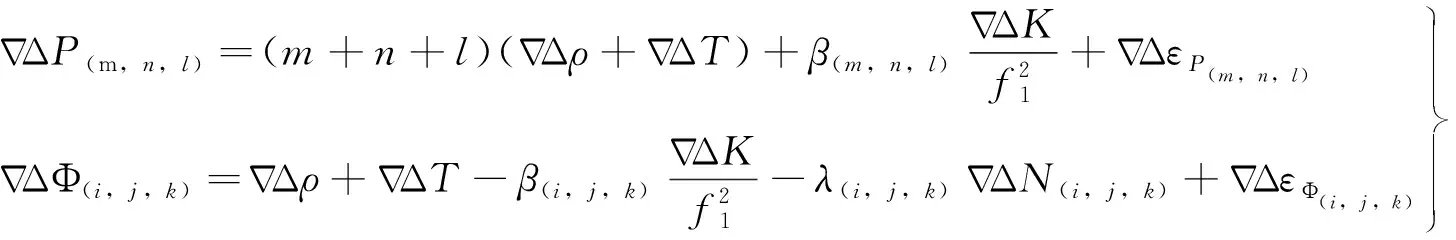
伪距和载波组合观测值分别为

(2)

(3)

式中Ps，fs，Φs分别为频段s的伪距、载波频率和载波观测值(s=1，2，3)。

组合观测值的波长、频率、模糊度[12]分别为

(4)

f(i，j，k)=i·f1+j·f2+k·f3

(5)

(6)

式中：c为光速；λs为频段s的波长(s=1，2，3)。组合电离层的延迟因子为

(7)

组合载波双差观测值噪声为

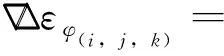
(8)

组合系数为(0，1，-1)和(1，4，-5)的超宽巷组合观测值的模糊度为

(9)

其中[]为四舍五入取整。

(10)

(11)

(12)

待宽巷模糊度固定后，可由宽巷观测方程和载波观测方程联立，求出B1频点的模糊度。宽巷观测方程和载波观测方程为

(13)

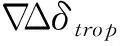
将式(13)联立可得B1频点的模糊度的计算式为

(14)

由式(14)得到的模糊度固定解标准差为0.208个周期，根据已得到的宽巷模糊度精确值，直接通过四舍五入取整，即得到精度很高的模糊度解。

1.2 基于BDS约束的GNSS模糊度固定

当BDS卫星的模糊度被固定后，将BDS卫星的双差观测方程与GPS/GLONASS卫星组成的观测方程联立求解出基线向量和GPS/GLONASS卫星的双差模糊度；已知的BDS B1模糊度精确值可以作为约束条件来加快GPS/GLONASS卫星的双差模糊度的解算。其误差方程为

(15)

V=AX′-L

(16)

当对式(16)进行解算求出GPS/GLONASS模糊度浮点解之后，利用LAMBDA算法对模糊度浮点解进行搜索固定。当模糊度被精确固定之后将其带入式(16)和式(17)中求解坐标向量X'和单位权中误差σ0为

(17)

式中：v为残差；p为权矩阵，n为每个历元中观测值的个数，t为必要观测值个数。

2 实验与结果分析

为测试本文GNSS单历元模糊度解算方法的精度和可靠性，采用一组实测的BDS/GPS/GLONASS 3系统短基线数据进行验证。数据采集时间为2016-07-17 T 00：00：00—24：00：00，采样间隔30 s，基线长8.4 m，截止高度角为10°，并且基站与流动站的精确坐标已知。根据本文提出的方法，首先固定BDS三频模糊度，再利用固定的BDS模糊度来计算GPS/GLONASS的模糊度。图2和图3分别表示BDS和GPS/GLONASS的可视卫星数目，可以看出在这24 h的时间内，BDS卫星个数为8～13颗，GPS/GLONASS组合系统观测的卫星个数为14～27颗。

图2 BDS可视卫星个数

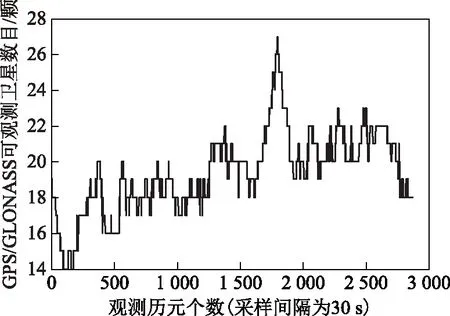
图3 GPS/GLONASS可视卫星个数

由图4可知，大部分时刻观测值的单位权中误差都小于4 mm，但是存在部分时刻结果较大的情况，最大值将近8 mm。

图4 单位权中误差值

根据模糊度已固定的BDS三频载波观测值作为约束求GPS/GLONASS的模糊度，在验证算法的有效性之前，数据中周跳已探测并修复。图5表示求解GPS/GLONASS模糊度时的Ratio值，可以看出本组数据大部分历元的Ratio值较大。载波观测值的噪声为2 mm，大于3倍中误差，认为错误，这里以Ratio>2[14]和Sigma0<0.002×3作为模糊度的固定条件，从结果可得到模糊度固定率为99.72 %；没有完全固定的情况主要是硬件或环境原因，造成0.28 %的历元BDS卫星数目不够。

图5 Ratio值

图6～8分别为N、E、U3个方向的坐标差值，从图中可以看出，N、E方向的差值大都在±20 mm之内，U方向的差值主要集中在±30 mm。表1是对单历元差分解算结果进行的精度统计，从表中可以看出，N方向的中误差(root mean square，RMS)为5.60，E方向的中误差为7.52，U方向的中误差为7.68 mm，并未出现比较大的偏差。

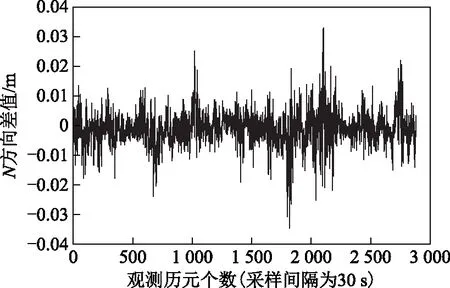
图6 N方向差值

图7 E方向差值

图8 U方向差值

表1 单历元差分定位结果RMS值mm

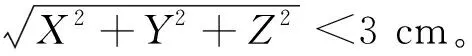
提出的方法求解BDS/GPS/GLONASS模糊度是准确可靠的。对于模糊度未能成功固定的，主要原因有2点：

1)宽巷模糊度固定错误；

2)观测噪声和电离层残差影响了BDS载波观测值模糊度的固定。

3 结束语

本文充分发挥了BDS三频点的优势，提出一种短基线GNSS单历元模糊度快速固定的方法，实测数据结果表明：1)利用三频观测值组合得到的超宽巷和宽巷组合观测值，可以更容易地固定模糊度，结果表明使用本文提出的方法模糊度固定率为99.72 %；2)使用模糊度固定的BDS载波观测值作为约束求解GNSS模糊度，不仅增加了观测方程的可靠性，而且提高了GNSS模糊度固定的效率，结果表明固定成功率能达到98.73 %，证明该方法对短基线而言是有效的。