韩江峪黏土心墙土石坝渗流及坝坡稳定性分析

张 录，王亮明，谢利云，刘 辉

(1.青海省水利水电勘测设计研究院，西宁 810007； 2.瑞和安惠项目管理集团有限公司，石家庄 050000； 3.河南天池抽水蓄能有限公司，河南 南阳 473000)

土石坝因具有就地取材、对地形地质及气候条件适应性强、施工管理方便等特点已被广泛应用。据国内外统计，土石坝失事事故约有40%是由渗流问题导致的[1]，因之导致的滑坡及渗透破坏甚为严重。因此，渗流分析及坝坡稳定性分析的可靠程度对土石坝的安全性具有重要影响。在土石坝内部渗流场中，浸润线以下区域为饱和渗流，而浸润线以上区域为非饱和渗流。但以往对土石坝的渗流分析多建立在饱和渗流基础之上[2-3]，没有考虑非饱和区的渗流情况，且在坝坡稳定性分析中较少考虑土体基质吸力的影响效应，导致分析结果与实际情况有较大差异。鉴于此，本文以饱和-非饱和渗流理论、非饱和土体抗剪强度理论及极限平衡分析法为基础，采用有限元分析软件GeoStudio中的SEEP/W及SLOPE/W模块对韩江峪水库黏土心墙土石坝进行渗流及坝坡稳定性分析，以期为类似工程土石坝的渗流计算及稳定性评价提供参考。

1 工程概况

韩江峪水库位于洋河支流西洋河上，是一座以防洪、灌溉为主，兼顾养殖等综合利用的小(Ⅰ)型水库。坝址以上控制流域面积2.34 km2，水库总库容131.09×104m3，死水位52.0 m，汛限水位61.5 m，正常蓄水位61.5 m，50年一遇设计洪水位62.59 m，300年一遇校核洪水位63.05 m。水库枢纽工程主要由黏土心墙坝、溢洪道及放水洞等组成，建筑物级别为4级。其中，黏土心墙坝顶高程63.5 m，坝顶宽4.0 m，坝顶长279 m，最大坝高15.9 m。上下游面均于高程55.9 m处各设有宽1.5 m的马道，上游面坡比自上而下依次为1∶2.5和1∶3.0，下游面坡比自上而下依次为1∶2.0和1∶2.5。大坝心墙底部设有黏土截水槽，下部强风化基岩层中进行帷幕灌浆，并深入相对不透水层2.0 m，大坝黏土心墙、黏土截水槽及坝基灌浆帷幕形成一个完整的防渗系统。大坝下游坡脚设有排水棱体，顶高程为49.5 m。坝基地质结构属土岩双层结构，上部为厚约5 m的砂壤土层，下部为黑云斜长片麻岩层。最大坝高典型横断面见图1。

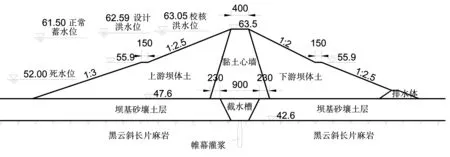
图1 黏土心墙土石坝典型断面(单位：高程为m，其余为cm)Fig.1 Typical section of clay core wall of earth rock dam (unit: height is m, and the rest is cm)

2 渗流计算分析

2.1 饱和-非饱和渗流模型

非饱和土体渗流同样符合达西定律，但与饱和土渗流相异之处为非饱和区土体渗透系数是土体基质吸力的函数，往往随空间位置而变化。由达西定律和流体运动连续性方程可导出二维非稳定饱和-非饱和渗流控制方程[4]为：

式中：kx(ψ)、ky(ψ)分别为X方向及Y方向的渗透系数函数；ψ为土体的基质吸力，即负孔隙水压力；h为总水头；γw为水的容重；mw为比水容重，定义为土水特征曲线斜率的负值，即：

式中：ua为孔隙气压力；uw为孔隙水压力；θw为土体体积含水量。

可见，在稳定渗流问题中，若已知渗透系数函数及边界条件，即可进行渗流计算。

2.2 计算工况

根据《碾压式土石坝设计规范》(SL 274-2001)，本文对黏土心墙坝稳定渗流期的水位组合情况进行渗流计算，具体工况如下：

1) 上游正常蓄水位61.5 m，下游无水。

2) 上游设计洪水位62.59 m，下游水位与河床表面齐平。

3) 上游校核洪水位63.05 m，下游水位与河床表面齐平。

2.3 计算模型及材料渗透参数

在GeoStudio软件SEEP/W模块中，根据大坝最大坝高横断面建立渗流有限元模型，见图2。模型中，坝基范围在顺水流方向自坡脚各向上下游方向延伸1倍坝高的距离，在深度方向取至相对不透水层顶部。采用以四边形为主的单元对计算区域进行网格划分，网格单元边长全局尺寸为1 m，对灌浆帷幕部分网格细化为0.5 m。

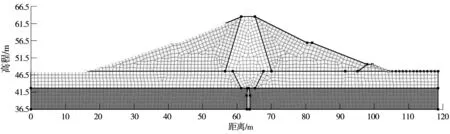
图2 黏土心墙土石坝二维渗流有限元模型Fig.2 Finite element model of two dimensional seepage flow of clay core of wall earth dam

渗流有限元模型的边界条件为：上游坝坡库水位以下部分及库底设为定水头边界，其值为相应工况库水位高程值；排水棱体下游坡面为自由渗出面(Potential Seepage Face)；下游河床面为定水头边界，其值为相应工况下游水位高程值；其余边界均为零流量边界，即不透水边界。

大坝各分区及坝基材料的饱和渗透系数根据室内试验并结合类似工程经验确定，见表1。由SEEP/W模块内置的样本材料土水特征函数和试验测定的坝体材料饱和体积含水率算出相应材料的土水特征曲线，之后由土水特征曲线、材料饱和渗透系数及模块内置的Fredlund-Xing模型[5]算出相应材料的渗透系数函数。坝体材料土水特征曲线及渗透系数函数曲线计算结果见图3。

表1 大坝各分区渗透系数Tab.1 The permeability coefficient of each partition of the dam

图3 坝体材料非饱和特性曲线Fig.3 The unsaturated characteristic curve of dam material

2.4 计算结果

应用SEEP/W模块分别对3种工况下的大坝进行渗流求解，可获得各工况大坝的浸润线、网格节点水头、节点流速、节点水力梯度、通过指定截面的渗流量等流场信息，可图形化显示结果。以工况Ⅰ为例，正常蓄水位作用下大坝浸润线及总水头等值线见图4。渗流计算的主要成果见表2。由表2可知，随着库水位高程值的增加，大坝心墙出逸比降、大坝单宽渗流量及下游坝坡出逸比降均增大。

图4 正常蓄水位作用下大坝浸润线及总水头等值线(单位：m)Fig.4 The dam infiltration line and the total head contour under normal water level (unit: m)

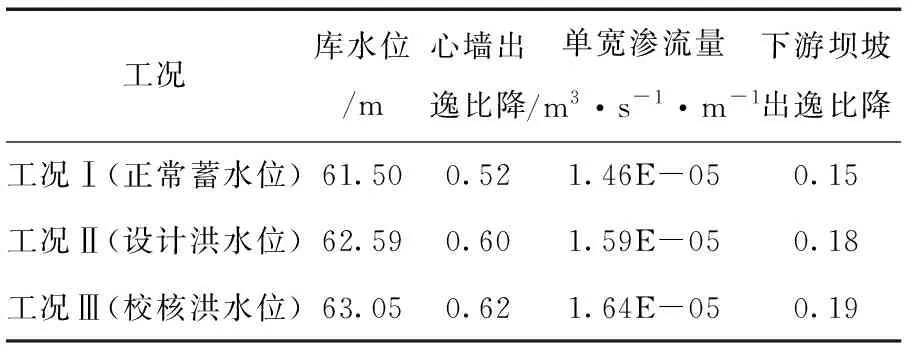
表2 大坝渗流计算主要成果Tab.2 Main results of seepage calculation of dam

3 坝坡稳定性分析

3.1 稳定性分析理论

非饱和土体Mohr-Coulomb抗剪强度公式为[6]：

τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb

(5)

式中：τf为土体抗剪强度；c′、φ′分别为土体有效黏聚力及有效内摩擦角；σ为法向应力；ua、uw分别为孔隙气压力及孔隙水压力；φb为基质吸力内摩擦角。

本文稳定性分析基于极限平衡分析原理，采用考虑条间法向力及条间切向力的Morgenstern-Price法[7]，依据静力平衡条件和非饱和土体Mohr-Coulomb破坏准则计算坝坡稳定性系数。

3.2 计算工况

稳定性分析的计算断面及计算工况均与渗流分析相同，针对每一种工况，分别计算大坝上下游坝坡稳定性。

3.3 计算参数

大坝各分区土层及坝基材料的物理力学参数见表3。

表3 大坝稳定计算材料物理力学参数Tab.3 Physical and mechanical parameters of dam on stability calculation materials

3.4 计算结果

采用SLOPE/W模块对各工况下大坝上下游坝坡进行稳定性分析，孔隙水压力采用相应工况下的SEEP/W模块渗流计算结果。以工况Ⅰ为例，正常蓄水位作用下大坝上下游坝坡最危险滑弧面见图5，各工况下坝坡稳定安全系数计算结果见表4。由表4可知，各工况下大坝上下游坝坡稳定性均满足规范要求。随库水位的增加，上游坝坡稳定安全系数逐渐增大。其原因为水体对上游坝坡的压重逐渐增大，使上游坝体内部法向应力增强，加大了土体颗粒之间的摩擦力，从而更有利于坝坡的稳定；随库水位的增加，下游坝坡稳定安全系数逐渐减小，其原因为随库水位的升高，下游坝体内部浸润线同时升高，指向坝坡外部的渗透力逐渐增大，使下游坝坡越不稳定。

4 结 论

综上所述，本文得出以下结论：

1) 随着库水位的增加，大坝心墙出逸比降、单宽渗流量及下游坝坡出逸比降均增大。

2) 各工况库水位作用下，大坝上下游坝坡稳定性均满足规范要求。

3) 随库水位的升高，上游坝坡的稳定安全系数逐渐增大，而下游坝坡的稳定安全系数逐渐减小。