基于FLAC-2D的蓄水过程某涉水滑坡体变形趋势研究

陈新新，汪绿培

(1.温州市瓯海区人民政府 瞿溪街道办事处，浙江 温州 325016； 2.瓯海区水利局，浙江 温州 325000)

1 工程概况介绍

某滑坡体位于金沙江与新滩溪交汇处，下距向家坝电站大坝39.4 km，陡崖下为崩滑体后缘，高程约为500 m；陡崖、缓坡相间，地形起伏大。滑坡体平面的面积约28.3×104m2，堆积体平均厚度15 m，主滑方向N20°E。

该滑坡体前缘分布高程300～410 m，体积约70×104m3，滑坡体上部分布有大量民房，且公路从滑坡下部通过，路面高程在387 m左右。据现场调查，该滑坡体在向家坝水库蓄水前局部地段已产生变形，水库蓄水至高程354.00 m后，变形进一步加剧，滑体上地表的房屋及地面出现多处裂缝和变形，且目前还有继续发展的趋势。

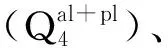
2 研究方法简介

本次边坡的稳定计算采用美国大型有限差分软件FLAC-2D[1-3]，主要使用渗流模块和边坡稳定计算模块。有限差分法渗流计算优势：根据渗流作用力概念，将作用在滑动面上和划分土块表面的水压力转换为等效体积力，同时把各节点水头值换算成各单元渗透力，不需要考虑各单元体接触面边界上的孔隙水压力，从而克服了一般条分法计算略去土条侧边水压力的误差，同时也不需要考虑边坡外水压力[4-7]。滑坡体中的地下水位随水库、河谷水位升降而变化，因而在滑坡体中就会形成饱和区和非饱和区。非饱和区土壤水与饱和区地下水运动密切相关，由于水运动导致边坡岩土体状态改变即为饱和与非饱和渗流问题，其渗透各向异性的饱和与非饱和渗流控制方程如下[8-10]：

式中：Kx、Ky分别为岩土体的水平和垂直方向的渗透系数；ρw为水的密度；mw为比水重；Q为边界流量；θw为体积含水率及ua；uw为空隙水气压与水压；h为压力水头；t为时间。

本次主要采用美国通用有限元软件ANSYS进行建模，之后导入FLAC-2D进行塑性计算，并运用强度折减法[11-13]计算边坡稳定性，其方法在数值模拟中较为常用，亦得到岩土工程界的认可。计算模型选取的应力场边界条件为：边坡底部采用水平和竖直方向的完全约束条件；左右采用水平约束条件；进行渗流场与应力场的耦合分析时，有限差分划分网格中的每个节点都创建了3个方程，两个平衡方程(位移)，一个渗流连续方程(孔隙水压力)。在耦合固结分析中，平衡和渗流方程同时被求解。ANSYS建立的滑坡体计算模型见图1，滑坡体各项物理力学参数建议值见表1。

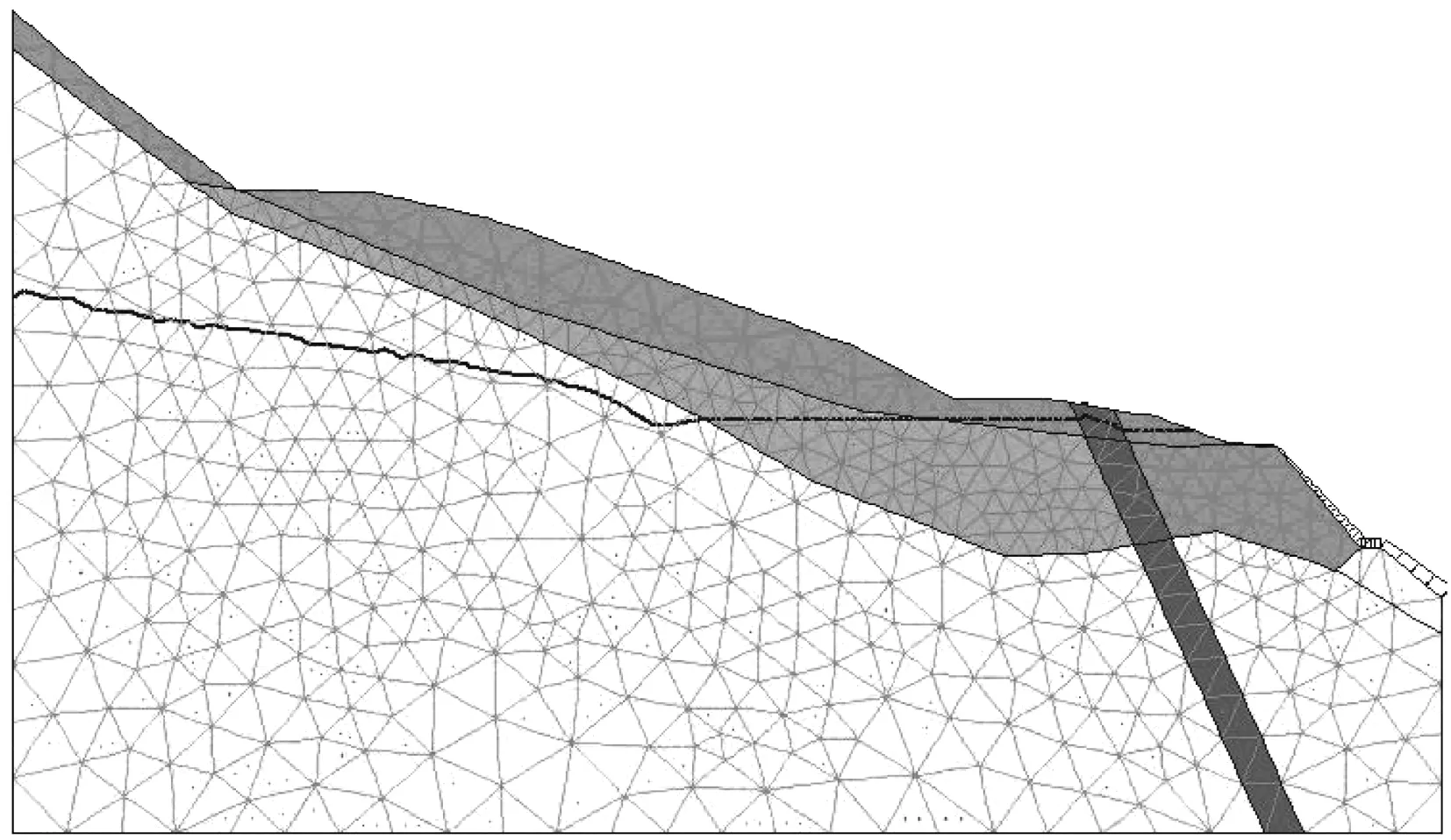
图1 滑坡体数值计算模型

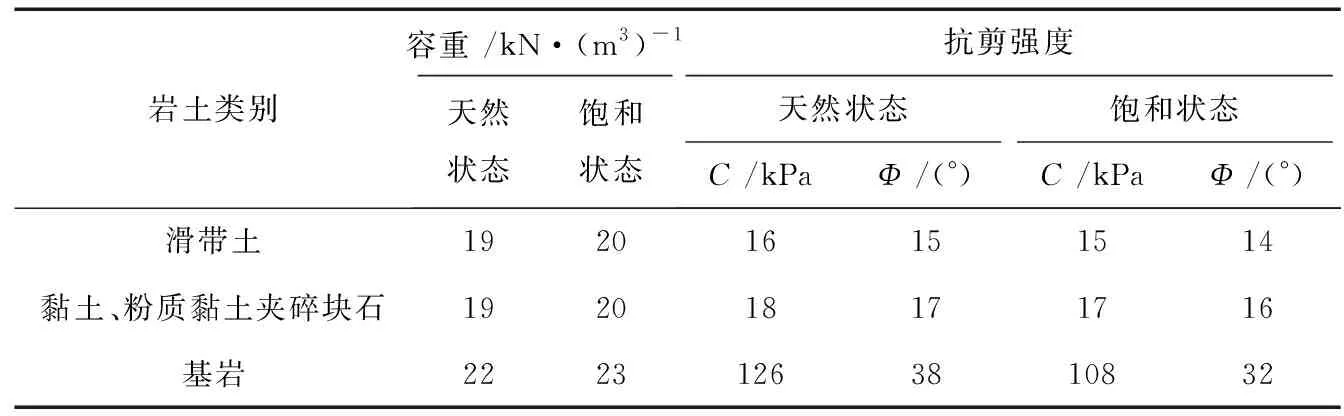
表1 滑坡力学参数建议值

为了定量计算蓄水过程中，随着水位逐渐升高，滑坡体的各项应力应变特性，选取计算的工况设置为：蓄水位354 m、水位上升至364 m、水位上升至370 m、水位上升至380 m等4个工况。

3 计算结果分析

3.1 水平变形分析

分析蓄水过程中坡内变形场变化，规定水平位移以顺坡向位移为正(向右)，逆坡向位移为负(向左)，具体计算结果见图2。分析可见，当蓄水位在354 m时，滑坡发生水平方向变形的区域主要位于滑坡前部，最大在1.5 cm左右；滑坡中部平台部位发生的位移稍小，大约在1 cm左右；滑坡体后部斜坡发生位移相对较小。随着蓄水位逐渐上升，当水位上升至高程364 m时，滑坡发生水平方向变形的区域主要位于滑坡中部平台附近，最大约3 cm，此时滑坡体前缘的变形基本趋于稳定。随着水位继续升高，分别升高至370和380 m后，滑坡发生水平方向变形的区域主要位于滑坡中前部位，最大约3.5 cm左右，而滑坡体后缘变形量稍小。

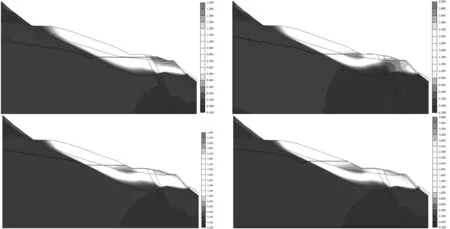
图2 滑坡蓄水位354～380 m水平阶段位移(单位：cm)

3.2 坡体内部应力应变分析

剪切应变是剪切时物体所产生的相对形变量，根据摩尔-库伦定理可知，剪切破坏是岩体最典型的破坏形式。因此，确定蓄水位上升过程中坡体内部的剪应变分布有助于了解滑坡体的破坏机理和趋势。根据计算结果，蓄水位分别在354 m、水位上升至364 m、水位上升至370 m、水位上升至380 m等4个工况的剪应变分布。见图3。

分析图3可知，当蓄水位稳定在354 m时，剪应变增量区主要分布在滑坡体前缘土体与基岩交界面处，滑坡体中后部的剪应变增量稍小；随着蓄水位的逐渐升高，剪应变增量的主要分布区转移到滑坡体中后部位置，此处深部的滑带土逐渐扩展，开始演化成滑裂面，但滑坡体前缘深部未贯通。通过计算，此时滑坡体安全系数约为1.1，认为滑坡体基本可以保持稳定，但稳定性较差。

勘探结果表明，滑坡体组成物质大致为黏土、粉质黏土夹崩(块)石、碎石，黏土呈可塑状，近地表部分呈硬塑状，连续分布厚度可达15 m，崩(块)石原岩为侏罗系中厚-厚层状粉细砂岩、泥质粉砂岩，裸露于地表的崩(块)石较少，直径不大，多在0.2～1 m。据勘探揭露，滑坡中部至后缘一带崩(块)石含量较之前缘有明显增加，直径也变大。在滑坡前缘的勘探钻孔表层揭露有冲洪积成因的粉质黏土夹砾石，厚度较小，在1.3～1.9 m，成分较杂，含量变化大，其分布范围一般在高程420 m以下。由此推断，滑坡堆积体厚度介于1.3～21.2 m之间，滑动方向70°，见图4。本次根据强度折减法计算了滑坡体的极限破坏面，结果见图5。计算结果基本与现场钻孔揭示的滑裂面一致，可认为本次计算结果基本合理准确。

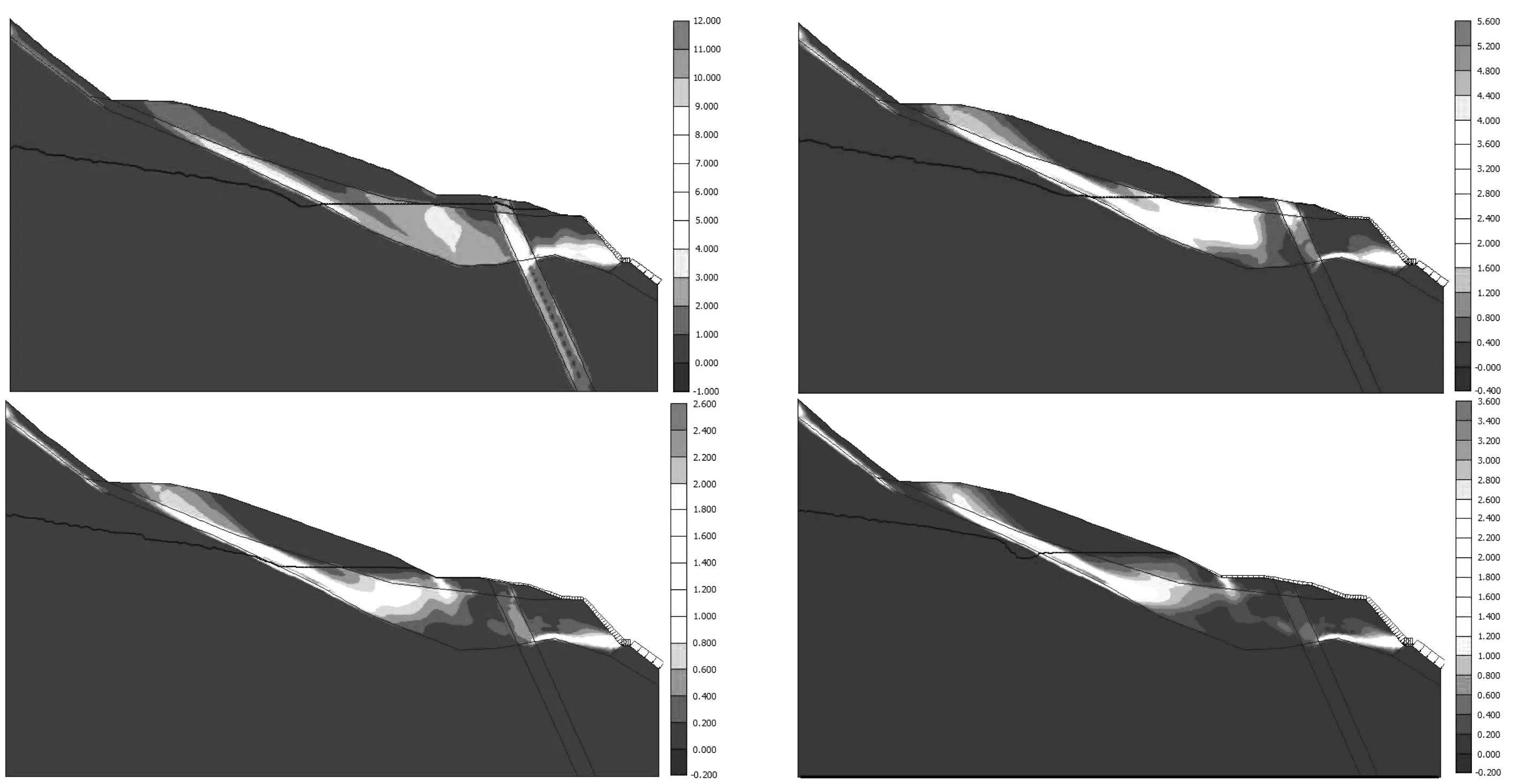
图3 滑坡蓄水位354～380 m剪应变增量分布(单位：10-3%)

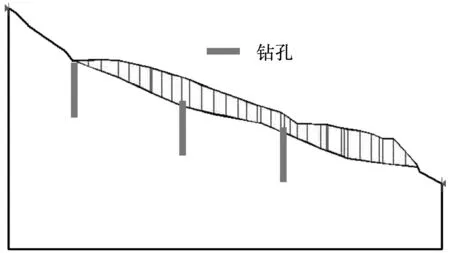
图4 现场钻孔滑带土推定的滑裂面

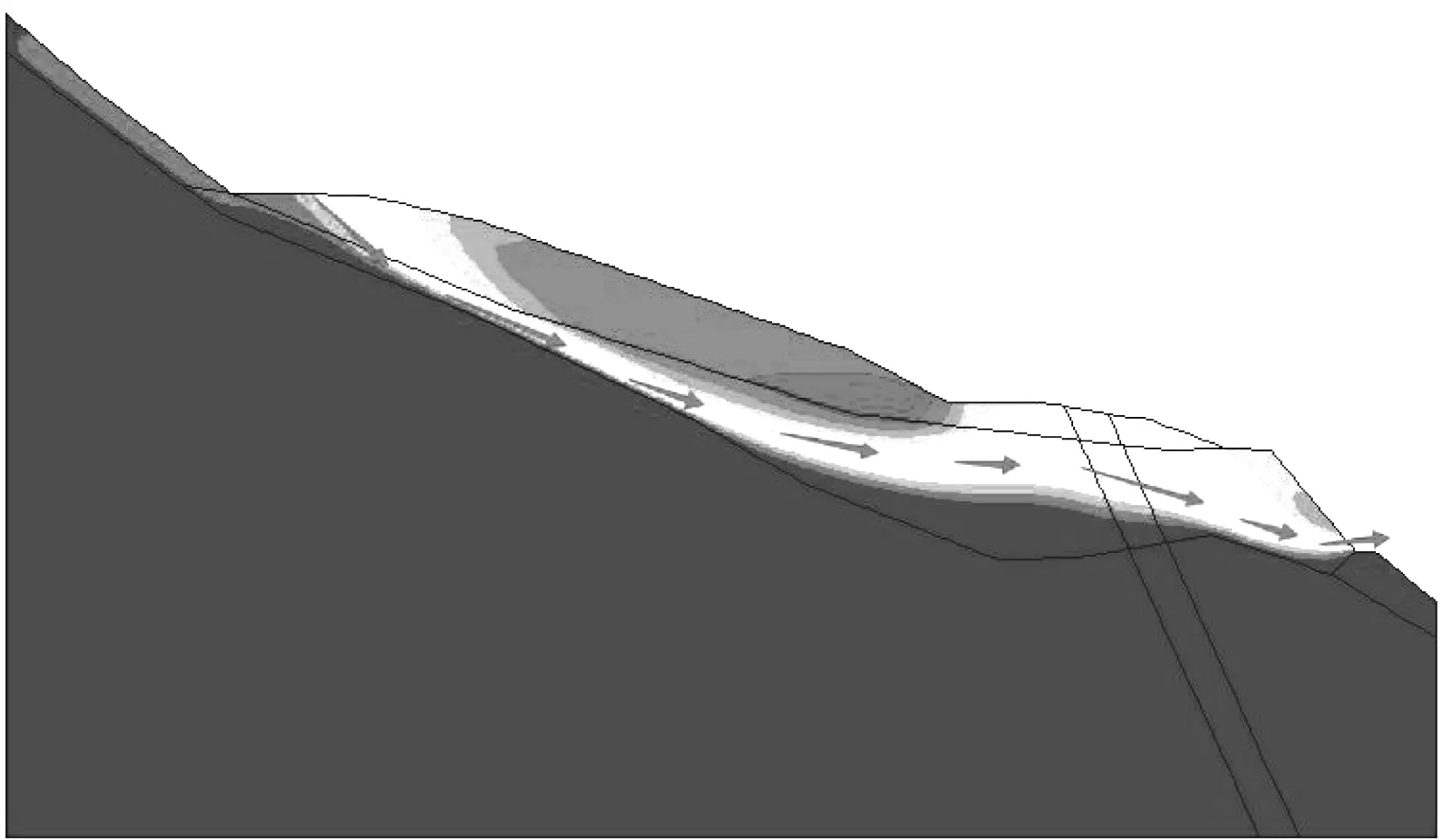
图5 滑坡体极限破坏滑裂面(Fs=1.1)

4 结 论

本文以有限差分软件FLAC-2D为计算平台，以某库岸滑坡体为研究对象，分析了蓄水位从354 m逐步上升至380 m的过程中该滑坡体的变形趋势，得到以下结论：

1) 在蓄水前期，滑坡体发生水平方向变形的区域主要位于滑坡前部，中部平台部位发生的位移稍小；在蓄水中期，滑坡发生水平方向变形的区域主要位于滑坡中部平台附近，最大约3 cm，此时滑坡体前缘的变形基本趋于稳定；在蓄水末期，滑坡发生水平方向变形的区域主要位于滑坡中前部位，最大约3.5 cm左右，而滑坡体后缘变形量稍小。

2) 当蓄水位在354 m时，剪应变增量区主要分布在滑坡体前缘土体与基岩交界面处，滑坡体中后部的剪应变增量稍小；随着蓄水位的逐渐升高，剪应变增量的主要分布区转移到滑坡体中后部位置，此处深部的滑带土逐渐扩展，开始演化成滑裂面，但滑坡体前缘深部未贯通。此时滑坡体安全系数约为1.1，滑坡体基本可以保持稳定，但稳定性较差。

3) 强度折减法确定的滑坡体极限破坏面与勘探钻孔确定的滑裂面基本一致，验证了FLAC-2D计算结果的合理性。