北方平原河道洪水演算方法探讨

雷德林，雷 蕾

(1.河北省沧州水文水资源勘测局，河北 沧州 061000； 2河北省保定水文水资源勘测局，河北 保定 071000)

1 概 述

随着经济的迅速发展，出山口后的河道洪水预报在防汛工作中越来越重要。但随着水利工程的建设及下垫面条件的变化，河道干涸的可能越来越大，对于北方河流可能性更大。自上世纪80年代以后，北方河流发生大中洪水的可能性越来越小、时间间隔也越来越长，如在河北省中南部1988年和1996年发生了较大洪水，时间相隔8年，1996年至今20年没有发生较大洪水。由于过水河道常年干涸，初始条件(糙率、河道下渗等)差别很大，并且每次过水时量级也不同，因此使用洪水历史资料率定过水河道参数是准确预报洪水的难题。随着中国洪水预报系统软件越来越成熟及水情通讯的迅速发展，实时校正参数的河道洪水演算方法用于洪水预报的条件已经成熟。该方法用当前实时水文信息对模型参数进行实时校正，让参数反映河道的当前状况，从而进行准确的预报。

2 实时校正参数法的原理

圣维南方程组中，式(1)是连续方程，是在考虑河道沿程损失情况下推导出的非恒定流连续方程，反映了水道中的水量平衡，其实质为流量与入渗量沿程变化之和等于河段槽蓄量的变化；式(2)为运动方程，该式表达了重力与压力的联合作用使水流克服惯性力和摩擦阻力引起的能量损失而获得加速度。

计算时，式(1)转化为河段水量平衡方程，式(2)简化为河段的槽蓄方程即：

Idt-Fdt-Qdt=dW

(3)

W=f(I,F,Q)

(4)

式中：dW为dt时段内河段槽蓄量的变化；I为河段平均入流量；Q为河段平均出流量；F为河段平均入渗流量。

设I′=I-F，那么式(3)和式(4)就简化为：

I′dt-Qdt=dW

(5)

W=f(I′,Q)

(6)

式中：I′为计算时段内指定河段的入流量与入渗量之差，相当于净入流量，联解式(5)、式(6)方程组的重点是河段的入渗水量的求算。

本文河道入渗水量的计算采用霍顿饱和入渗方法，求出河段净入流量后，再用马斯京根分段演算法对河道流量进行连续演算。

霍顿下渗曲线经验公式为：

f=fc+(f0-fc)e-kt

(7)

式中：f为入渗率；fc为稳定入渗率；f0为初始入渗率；k为与土壤特性有关的经验常数，其与河床的物理特性有关；t为时间。

如果计算河段河宽、河段长分别用B和ΔL表示，则时段Δt内的入渗量F为：

F=B×ΔL×f×Δt

(8)

马斯京根法是一种基于槽蓄方程和水量平衡方程的河道流量演算法，由于使用方便，精度也较高，在生产实践中得到广泛的应用。马斯京根河道流量演算公式：

Qt=C0It+C1It-1+C2Qt-1

(9)

式中：It、It-1分别为上断面t和t-1时刻的流量；Qt、Qt-1分别为下断面t和t-1时刻的流量；C0、C1、C2为洪水演算系数，可由下列各式确定：

式中：Δt为时段长；k为蓄量参数；x为马斯京根参数，为入流和初流对槽蓄影响的相对比重，它与洪水波的传播速度、扩散系数及河段长度有关；K和X根据所研究的河道特性和洪水特性来决定，并假定为常数。

为了利用式(9)、式(10)求得洪水演算系数C0、C1、C2，必须首先确定其中的Δt、k和x。为此，除了演算时段长Δt可根据问题的要求确定外，k和x则需要根据实测洪水资料进行确定。然后在按照式(9)逐时段计算，即可求得各时段下断面的流量过程。

3 预报方案构建

3.1 所需资料

实时校正参数河道洪水演算方法需要的数据资料：河道入口既有的流量过程和相应流量在出口的延续过程；计算河段的长度及平均水面宽。

3.2 计算方法

给定模型初始参数，根据第一个单元河段入口入流量I1，求出该河段的入水量，按R.E.Horton公式计算t时刻的下渗率；再由公式Ft=ft×B×L×Δt计算该时段内下渗量，将计算出的下渗量与第一河段入水量进行比较，如果河段入水量小于时段下渗量，则第一河段净入水量认定为零。依次计算下去，直到当第一河段的河段入水量大于时段下渗量时，求出第一河段净入流量，然后采用MSK法将净入流量演算至第二河段，第三河段……，直至演算到计算河段出口为止。将出口流量过程与实测流量过程进行全面比较，若差距较大，则应下渗参数和流量演算参数进行调整，再进行计算，直到误差达到允许为止。

3.3 预报方案构建

给定下渗参数和河道洪水演算参数的初始值及范围，其中计算时段长是报汛时段长，河道长度是从入口至出口长度(即上断面至下断面长度)，都是固定值，无需优选。根据上断面实测流量资料及下断面相应初始流量资料确定参数，参数的初选采用罗森布朗克法，精选采用单纯型法，用优选好的参数对下断面流量过程进行演算。随着下断面实测流量资料的增加，逐步对参数进行优化，可以使演算精度进一步提高。

4 应用与检验

4.1 预报河段的选择及资料情况

本次分析选择河北省常年干涸的平原河道滹沱河黄壁庄～北中山段1996年大洪水资料、引黄济津输水河段河北省三郎～连村段2004～2005年资料、常年过水的黄河下游高村～孙口段2008年汛期流量过程资料。

4.2 实时校正参数河道洪水演算方法分析

选择常年干涸、常年过水及输水河道这3种有代表性的断面，对不同时段的流量过程进行参数优选率定，然后演算下断面流量过程。3个河段参数率定结果见表1，演算成果见表2。

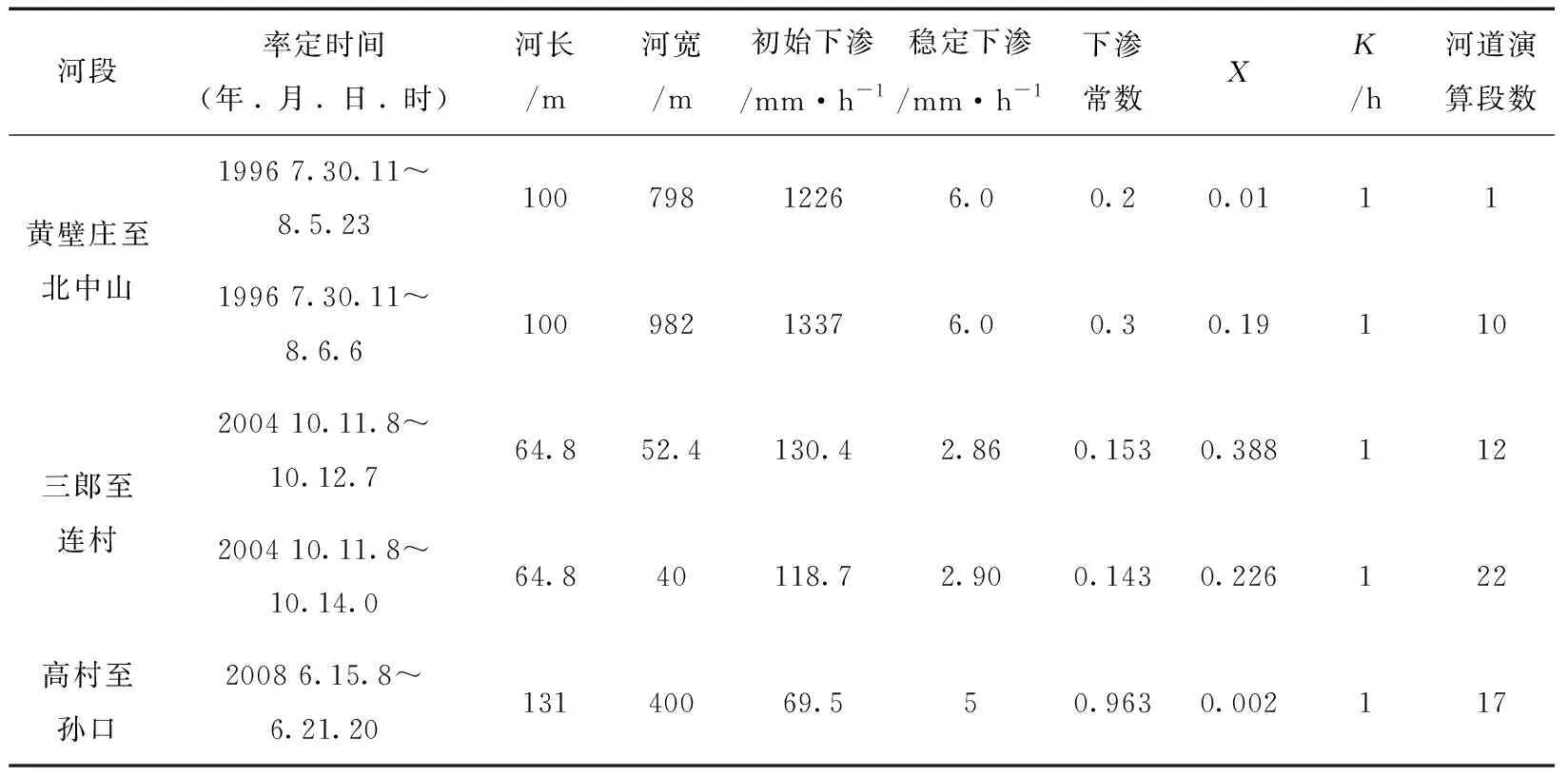
表1 实时校正参数河道洪水演算参数率定成果表

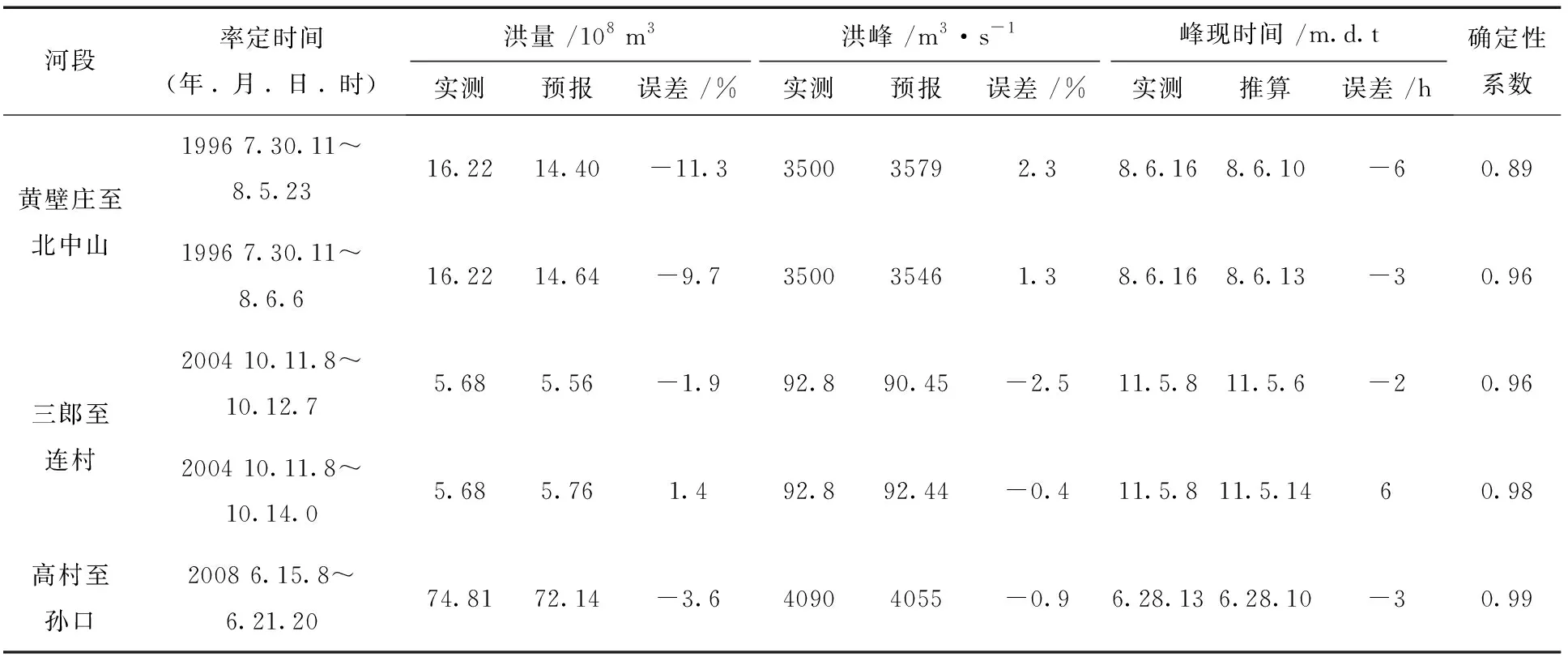
表2 实时校正参数河道洪水演算成果表

由表2演算结果可见，实时校正参数河道洪水演算方法在常年干涸、常年过水及大洪水、小水等各种河道洪水演算应用的效果较好。本次分析选择了3个河段3次洪水，其中滹沱河1996年为干涸河道过水。分析中先选取北中山站7月30日11时～8月5日23时的流量资料进行参数优选率定，其演算结果洪量偏小11.3%，洪峰偏大2.3%，确定性系数0.89；然后选取7月30日11时～8月6日6时再次进行参数优选率定演算，结果洪量偏小9.7%，洪峰基本吻合，确定性系数达0.96(图1)，演算结果明显提高。引黄济津输水河段三郎～连村段最初选取端庄刚开始起涨(10月12日7时)进行参数率定，其演算结果洪峰偏小2.5%，洪量偏小1.9%左右，确定性系数0.96；之后将连村站流量选取到14日0时，再次进行参数优选率定，结果为洪峰基本吻合，洪量偏大1.4%，确定性系数达0.98(图2)。黄河下游常年过水的高村～孙口段只率定了2008年汛期开始6天的资料，整个汛期演算结果的确定性系数就达到了0.99，洪峰、洪量误差均在5%以内，峰现时间误差在5 h之内(图3)。

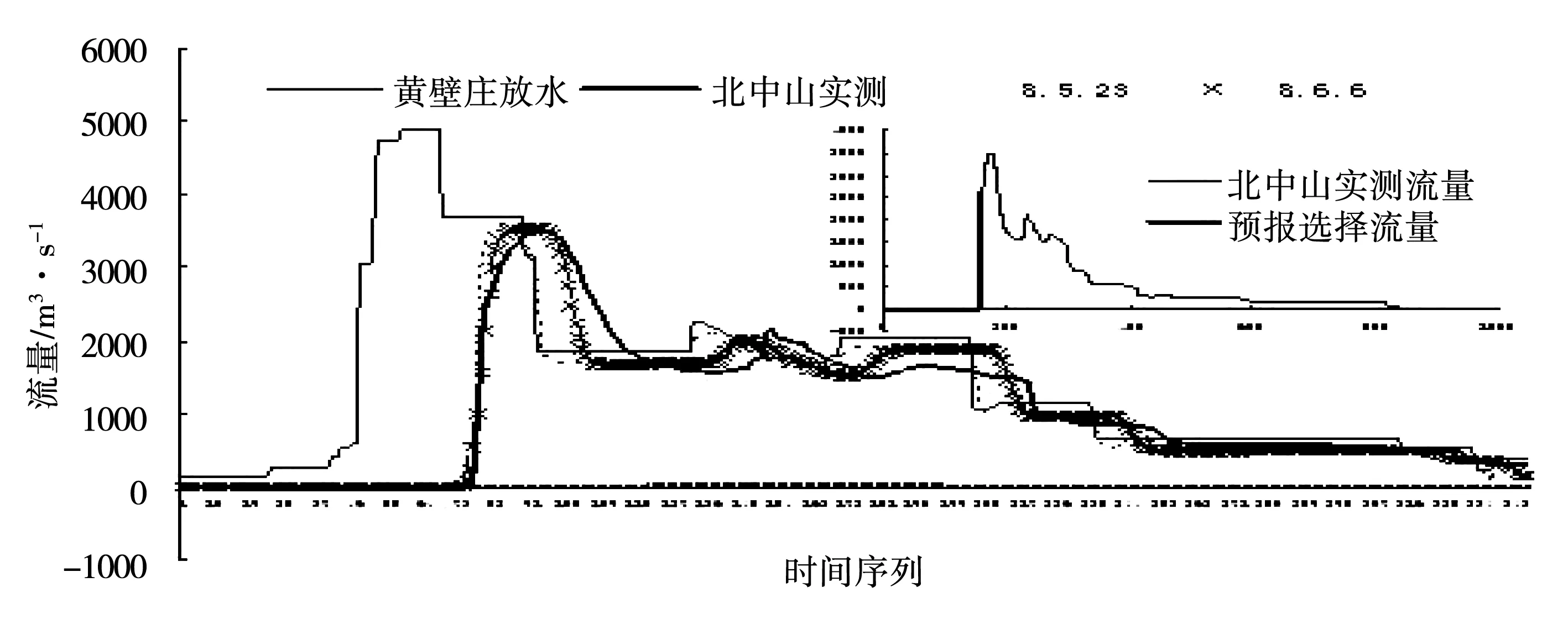
图1 滹沱河黄壁庄～北中山段实时校正参数河道洪水演算(1996年)

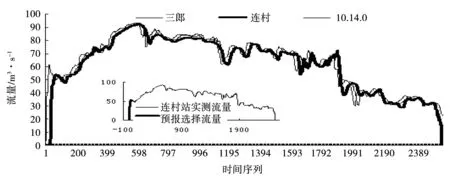
图2 三郎～连村段实时校正参数河道洪水演算(2004年)

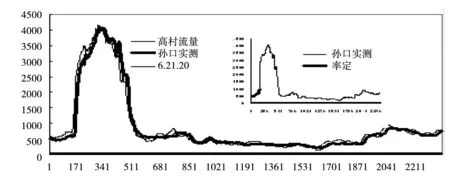
图3 2008年黄河高村～孙口段实时校正参数河道洪水演算

5 结 论

1) 提出实时校正参数河道洪水演算方法，通过在常年干涸、常年有水及输水河道并考虑各量级(大洪水、小水等)的流量过程进行分析研究，其预报结果精度高，方法适用面广。

2) 实时校正参数河道洪水演算方法将MSK(马斯京根河道演算)与R.E.Horton(霍顿饱和下渗理论)有机组合在一起，考虑了河道沿程损失，为常年干涸的北方河道洪水预报提供理论支持。

3) 以中国洪水预报系统为平台，实现了实时校正参数的河道洪水演算，方法简单可行。该方法涉及参数少，物理意义明确，并易求得，易于推广。