平面几何命题建议：回归教材与坚守课标——从2018年北京中考卷第27题说起

☉江苏省泰州市姜堰区实验初级中学 许小燕

每年全国各地中考试卷几百份，真是尽显中国文化的丰富多样.仅就平面几何这一块的考查来看，各地的考查重点、难点真可谓“天上人间”，国家层面的“课标”对平面几何的教学要求似乎都被一些地方的命题专家们忽视，只是在填写命题“双向细目表”时，才想起把自己刻苦、深入钻研出来的几何难题贴上教材上某页某题是原型的标签.然而，作为首都北京的中考试题，在全卷倒数第二题竟然考查了一道教材上的经典几何题，让很多人不解，认为北京这是在降难度、送分给学生.然而笔者有不同看法，本文就从北京这道几何综合题说起，提出一些自己的思考，抛砖引玉.

一、从北京考题说起

考题 （2018年北京卷，第27题）如图1，在正方形ABCD中，E是边AB上的一动点（不与点A，B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH.

（1）求证：GF=GC；

（2）用等式表示线段BH与AE的数量关系，并证明.

图1

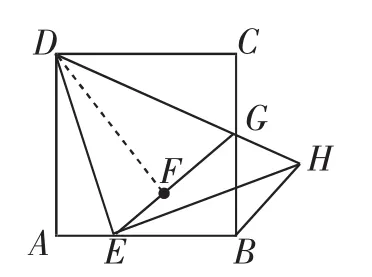
图2

思路简述：

（1）根据“点A关于直线DE的对称点为F”想到连接DF，这样待证的“GF=GC”在△CDG和△FDG中，只要证它们全等即可.这样思路就连通如下：

先证△ADE≌△FDE，可得AD=DF，∠DFE=90°，再借助于正方形ABCD的边长沟通出DF=DC，∠DFG=90°，于是Rt△CDG≌Rt△FDG.从而问题获证.

（2）先由（1）问“成果扩大”，在图2中，△ADE≌△FDE可带来∠ADE=∠FDE，Rt△CDG≌Rt△FDG可带来∠CDG=∠FDG，于是∠EDG=∠ADC=45°，进一步，可确认△DEH是等腰直角三角形.这时我们将问题删减无关线条，得出图3这样的简化图形，当然这也是一个熟悉的“教材图形”（八年级平行四边形一章中有类似习题）.

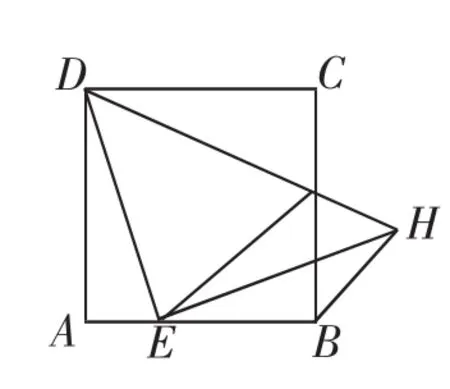
图3

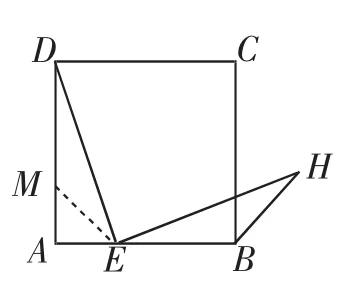
图4

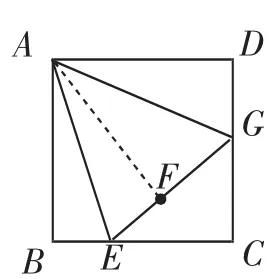
图5

一个典型证明思路：如图4，在AD上截取AM=AE，构造等腰直角三角形AME，再证出△DME≌△EBH.即可把BH转化为ME，从而实现问题突破BH=ME=AE.

二、回顾反思

北京卷出来后，有些老师对这道考题很是不解，说北京卷“倒二”怎么考了一个“老掉牙”的考题？熟题出现在这么重要的位置，似乎有些不可思议.笔者有不同见解，以下先对两个小问所涉及的基本图形梳理如下：

第（1）问涉及的所谓“半角模型”，如图5，设E、G为正方形边BC、CD上的点，则下列命题等价：

①∠EAG=45°；②△CEG的周长等于正方形ABCD周长的一半；③EG=BE+DG.

第（2）问涉及一道教材经典问题，如图6，四边形ABCD是正方形，点E是边AB上一点，∠DEG=90°，EG交正方形外角的平分线BG于G.求证：DE=EG.

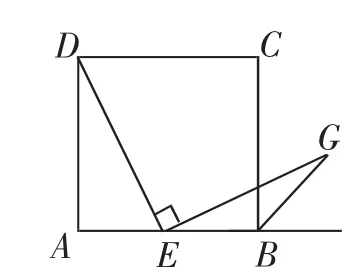
图6

图7

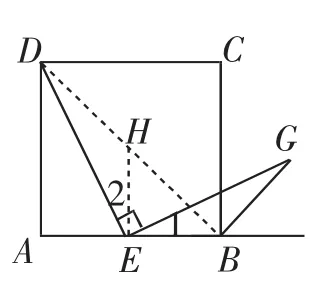
图8

这道经典问题各种版本教材上都有，除了上面提供的构造思路是有效的，以下两思路也是常见的：

思路1：如图7，在DA延长上截取AN=AE，构造等腰直角三角形ANE，再证△DAE≌△BAN，进一步证出平行四边形BGEN；

思路2：如图8，连接BD，作EH//AD，交BD于H点，可证△DEH≌△EGB，获证.

三、关于几何综合题命制的思考

第一，严守课标，中考平面几何的命题不宜创新

《义务教育阶段数学课程标准（2011年版）》对第三学段平面几何的各个知识点都有明确的要求，比如关于“图形的相似”有如下表述：“了解相似三角形的判定定理：两角分别相等的两个三角形相似；两边成比例且夹角相等的两个三角形相似；三边成比例的两个三角形相似.”可以发现，相似三角形的判定只是“了解”要求，而检索各地中考试卷最后一道大题，涉及复杂相似的综合题不在少数，有些涉及需要多次相似，而且需要添加辅助线构造相似来处理，对比课标“了解”要求，似乎都有些超标了.这样来看，中考平面几何的命题考题，就不必过分创新，特别是由某个平几图形出发，深入挖掘图形中的很多奇异性质，并精心伪装，让学生通过较为复杂的辅助线构造，才能转化为一种所谓的模式图形或基本图形，也许这些探究在平时的教学或课外拓展挑战中更加适合一些，而对于中考这样的全员参与式的“毕业、升学”两考合一的考试命题来看，还是应该严守课标不走样，不打擦边球，特别是不能凭着命题组个别成员的平面几何兴趣，设计出一些个性化成分很高的较难平几题，这是对课标的理解和执行不到位，需要对照课标启动问责的命题行为.在这里我们还可提及这样一种事实：高考数学试卷中，往往也有一道平几何试题，但是难度只相当于中考试卷中的几何的中档题的难度；那些较难的平几难题基本都是出现在高中数学竞赛试题中，而高中数学竞赛参与的学生只有极少数.在这个人数比来看，有些中考试卷中设计出一些很难的平面几何题作为把关题实在是出力不讨好的尴尬做法.笔者就曾听很多高中老师抱怨：“你们初中教了那么多的平几难题，我们高中又不再学习，何苦浪费很多学生时间，影响学生数学学习的信心与兴趣呢？”

第二，回归教材，重视教材经典问题的变式考查

如上分析，严守课标的平面几何命题不宜过分创新，那么一个重要的操作方法就是回归教材，重视教材经典问题的变式考查.具体来说，初中教材上有很多例题、习题都有大量的经典问题，这类问题教材上练过、讲过.有些命题者一方面在写“命题双向细目表”时每道题都对应着教材上相关例、习题，然而另一方面对所谓教材原型问题改编得面目全非，所谓原型出在教材第几册第几页，只是标签式的解释，不值一驳.而北京卷这道正方形考题就给我们提供了如何把教材问题进行变式考查的示范.也就是在经典问题的呈现方式上进行适度包装，待学生解读条件之后就会有熟悉的经典问题出现，从而顺利解决问题，重在整理规范的几何推理语句进行表述和推理书写.

第三，理解数学，平几教学价值着力点在于推理

根据章建跃博士提出的“三个理解”，其中理解数学是第一位的，不只是课堂教学需要理解数学，对于命题（中考、期末、学业水平测试等各级考试命题）都需要把理解数学放在第一位.很多命题中的乱象，根本上说就是理解数学出了问题.比如平面几何的命题，这些年不少地区以函数图像为背景、平面直角坐标系为平台，引出平面几何的一些复杂模型、各种变换后探求某些点的存在性，本质上说这些问题都是平面几何问题，与所给的坐标系、函数图像无甚联系，虽然最后也要求点的坐标、或某函数图象的解析式，然而问题的真正难点是“超越课标要求”的几何模型与辅助线构造，这就使得学生负担加重，进入题海，大量练习这些伪坐标系考题，到头来出现一些学者眼中的“怪怪的试题”（北京 贺信淳老师），既不是函数题，也不是平面几何题.我们现在的义务教育阶段仍然保留了平面几何教学内容，但随着数学的发展，平面几何中也有很多繁难内容需要舍弃，保留很多经典内容的教育价值主要为了发展学生的逻辑推理能力，而不是繁杂或奇异几何性质的学习.因为义务教育阶段平面几何是普适性，面向全体学生，从这个角度看，“课标（2011年版）”再次降低平面几何的要求，特别是对圆的很多内容、相似的要求不断削弱是值得肯定的.相应的，各级命题人员应积极跟进，严格执行国家层面课标要求，降低中考对平面几何的考查要求，回归教材经典习题的考查.对个别地区无视国家课标要求的，“个性化”命制超标几何题的命题行为，教育行政主管部门要加强命题培训和试题评审，让命题超标现象越来越少.