一种基于界面传播的干涉相位快速解缠方法

高 建，石 磊，夏 宇，沈佩姗

(1. 南京邮电大学地理与生物信息学院，江苏 南京 210046； 2. 南京邮电大学通信与信息工程学院，江苏 南京 210046)

二维干涉相位解缠处理是干涉测量技术中的关键步骤，在InSAR、InSAS及光学干涉处理中应用广泛。相位解缠所解决的关键问题是相位采样数据中的不连续性问题，即受到目标特定地形、采集系统或环境噪声等因素的影响下，采样数据不满足奈奎斯特定理条件的情况。围绕相位解缠开展的相关研究主要集中于直接或间接探测不连续边缘，尽量抑制不连续边缘对绝对相位推算的不利影响范围。比较常用的解缠方法包括支切法[4-5]、质量引导法、最小范数法等，实用效果较好的则是基于最小费用流[1-3]的SNAPHU方法。支切法[4-6]是通过直接搜索残差点之间的连接关系，匹配合适的残差点对形成支切线作为不连续边缘的标记，在进行推算相位值时避开支切线即可保证相位数据连续，方法简单易行，执行效率高，但存在错误匹配可造成区域性的影响及空洞和孤岛的问题。质量引导方法[7-10]主要是通过相位数据质量的信息，提供推算路径的引导信息，这种方法实用效果并不好。最小范数类方法是通过不连续边缘的范数最小化原则，解算解缠相位，结果一般较可靠，稳定性好，但常常涉及迭代解算大型稀疏线性方程求解，计算量大，不适宜大型数据处理。基于网络流的方法则是通过将残差点进行连接，构建符合最小费用原则的网络图，用来描述不连续边缘的分布，这种方法实用效果较好，但是在数据质量不高、残差点数量较多的情况下，运算量较大，解算效率较低。随着观测技术的进步，数据重复采集的周期越来越短，数据时空分辨率越来越高，数据量越来越大，对于大数据量的解缠处理提出了更高的要求。要求方法可靠性高，同时运算效率高。

本文在前期研究成果[11-12]的基础上，利用综合残差点和数据质量的分布信息的可靠度指标值，提出一种基于界面传播的快速二维相位并行解缠方法。

1 原理方法

1.1 基本原理

本文方法是在一种可靠度测量指标的基础上进行研究。这种衡量相位数据可靠度的指标是基于表征不连续边缘的残差点位置和数据质量分布的综合描述。可靠性指标P参考残差点S在(x,y)处的定义可以描述为沿着两点间连接路径的质量函数积分

(1)

式中，Q为描述相位数据质量的正的增函数；c为连接残差点和目标点的路径。由于两点间存在无数连接路径，这里选择获得最小积分值的，即

(2)

数据中存在多个残差点，参考点也是选择最小积分值对应的点作为最终选项，即

Pf(x,y)=min{PS(x,y)S∈R}

(3)

式中，R为定义域内所有残差点的集合。这种指标即作为描述相位数据可靠性的量化描述。

在相位解缠过程中，根据基准相位数据和解缠积分路径，绝对相位Φ的推算公式为

式中，Φ0为基准相位数据；c为梯度积分路径。一般选择较为可靠的积分路径，积分路径的可靠性衡量值可以参考路径上最低值，即

P(c)=min{Pf(x,y)(x,y)∈c}

可靠度最高的积分路径为

(4)

因此，最终获得可靠的解缠相位为

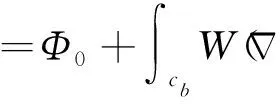
(5)

根据式(5)可以推算最终的解缠结果。直接根据式(2)和式(4)进行处理需要考虑全局排序或搜索的问题，而这类操作对于大块数据处理的效率不高。本文使用并行处理模式，通过并行迭代方案替代串行搜索实现加速。

1.2 并行设计方案

并行解缠处理方案是基于单指令多数据流(SIMD)的操作模式，将数据划分成小块处理单元，主要的处理在分块内部与分块之间进行，界面的传播移动也是以这2种方式呈现。

不论是以离散像素点为目标单元的块内处理，还是以分块为单元的块间处理，界面的移动传播都是通过处理单元的状态变化实现。如图1所示，处于过渡状态的界面A-B-C-D-E分隔了左侧的已处理和未访问的2种状态。当单元C完成处理，其状态会变为已处理，邻近的F成为新的界面元素，实现了界面向A-B-F-D-E的移动。

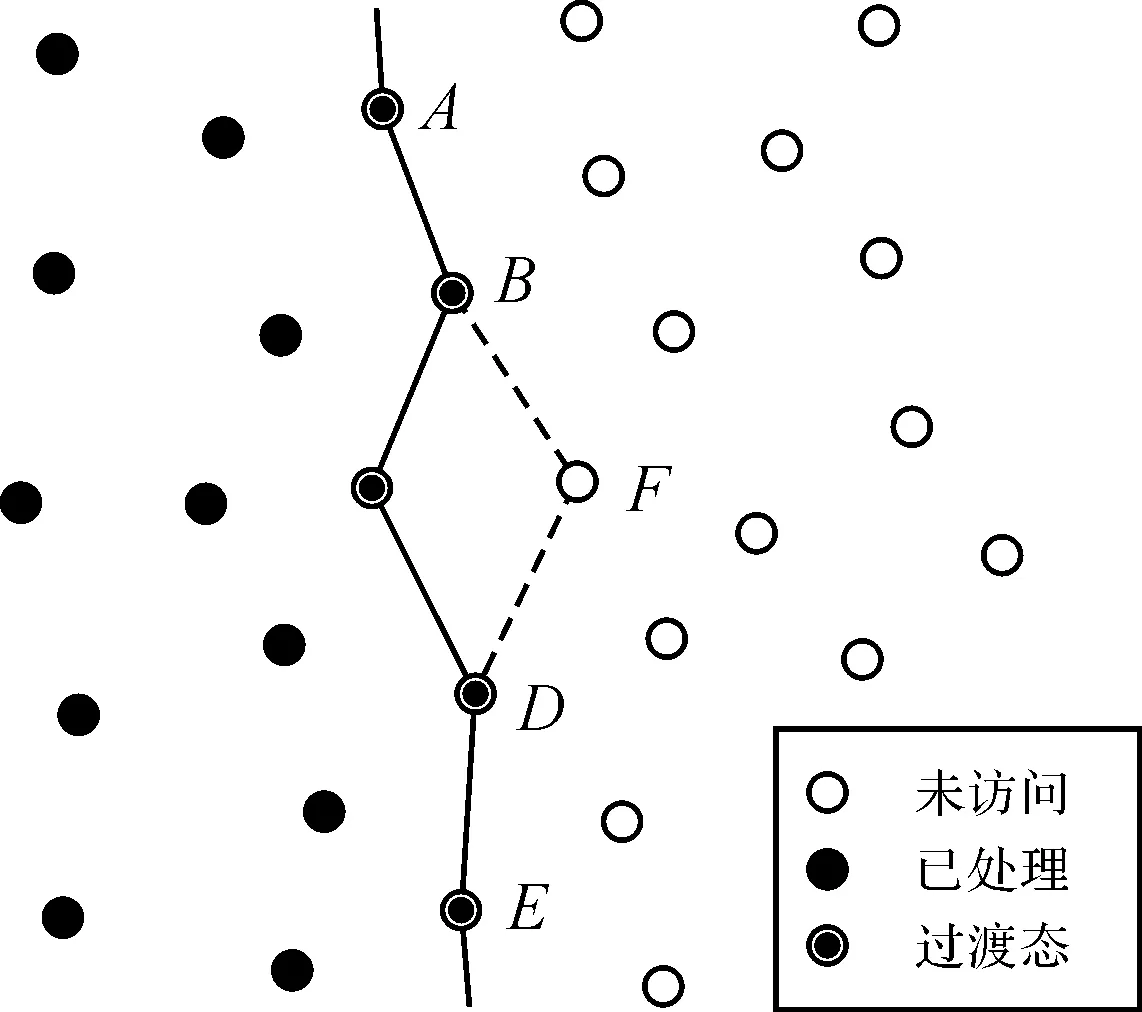
图1 离散域内的界面移动示意图

在正向传播过程中的处理，主要是根据可靠度指标定义，由已知点向未知点传播，解算的主要依据是表述可靠度与质量指标的程函方程

(6)

具体计算方法可以根据Godunov逆风方案实现。

在反向传播过程中，需要以可靠度较高的基准相位为基础，向可靠度较低的区域传播延伸，在传播的过程中完成绝对相位的解算。优先解算的相位相对具有较高的路径可靠度，最后解算过程收敛于相位不连续边缘位置。因此在反向传播过程中，重点在于邻近最可靠路径的判定。

无论是正向过程还是反向过程，无论是块间传播还是块内传播，解算时都会面临充分度问题，即解算时只有部分可用临近点的情况。如栅格网中点的四邻域内，只有1或2个可用，而不可用的邻域点在后期变为可用时可能会影响重新解算。在这种情况下，已处理的离散点或分块的取值，在其邻域发生更优化的变化时，存在重新解算的需要。这种现象由忽略全局搜索造成，主要的解决手段就是迭代处理。根据定义，迭代解算邻近单元间的待定值，解算结果逐步趋向最优取值，当迭代收敛时，取值稳定，终止处理。当分块内所有离散点计算收敛，则定义分块收敛，当所有分块收敛，则整个解算过程完成。

1.3 实现流程

前述块内处理和块间处理方法，都是基于平行模式的处理方案。整个解缠数据处理的过程如图2所示。

首先针对缠绕数据，获取其相位质量指标数据。这种数据可以以附加信息的方式直接提供，也可以从数据本身统计获得，如相干系数、缠绕梯度方差等指标，将其变换为正递增形式即可。残差点探测，即通过缠绕梯度的回路积分，寻找非零积分值即标记为残差点位置。残差点是正向传播的起点，其位于不连续边缘上，可靠度设置为最低值，0值残差点所处分块设置状态为活动，标识传播界面所处位置。

正向传播的过程即是循环块内处理和块间处理的过程。块内迭代至块收敛，状态变为收敛，然后考察其非活动领域块，有正向影响的领域块设为活动状态，接着进行下一轮迭代直至所有块都收敛。

设定基准相位区域后，其所处分块设置为反向传播的其实活动块。块内迭代至块收敛，状态变为收敛，然后考察其非活动领域块，有正向影响的领域块设为活动状态，接着进行下一轮迭代直至所有块都收敛，完成相位解缠处理。

2 试验与分析

试验采用机器配置为CPU(6核，1.9 GHz)×2，GPU(15个处理单元,2880核，0.75 GHz)×1，12 GB设备内存，32 GB主机内存，64位操作系统，C++语言环境编码实现。

试验数据采用Envisat的2015年的一幅干涉相位数据，如图3中(a)所示。数据尺寸6132×5599像素，包含残差点31 709个。数据质量指标采用缠绕相位梯度方差统计值计算，即

式中，ε是一个很小的正整数，防止出现分母为零的情况。

全部数据按照4×4的尺寸分解，共分2 146 200小块，根据残差分布设置正向传播的初始活动块，然后进行可靠度指标数据计算。正向传播获得数据如图3(b)所示，由图中可以看出，可靠度指标较高区域，残差点被分割包围在较小的独立区域内。

设置可靠度最高的相位信息为基准相位，对应的分块为反向传播的起始活动块，按照优先高路径可靠度相位推算的原则进行绝对相位解算，则高可靠度区域会优先覆盖连通，保证了解缠数据的可靠性。解算结果如图3(c)所示。

为做对比，同时应用SNAPHU方法进行解缠处理，处理结果如图3(d)所示。直观上的对比，两种方法得到的结果几乎没有差别。

为做进一步的量化对比分析，本文统计了2种方法处理结果中的相位不连续边缘的L0范数和L1范数值，以及2种方法处理数据所用时间，可以大体反映2种方法的数据质量和处理效率，统计结果见表1。

根据表中的统计数据的对比，可以发现，SNAPHU方法得到的结果，不连续边缘最小范数的统计结果相对较好，但是数据处理效率上，本文方法具有压倒性的优势。

表1 SNAPHU与本文方法解缠试验统计结果

同一数据使用SNAPHU处理需要运行接近50 min，而本文方法所用时间不到10 s，这种效率上的优势在处理大尺寸、海量数据时显得尤为重要。

至于质量统计指标上的差距，根据推测应为采用质量指标的问题，SNAPHU采用二维向量式的代价函数，而本文方法采用向量范数，模糊了各向异性的情况，容易导致边缘细节精度稍差。

3 结 语

本文提出了一种基于界面传播的并行相位解缠方法，首先利用残差点和数据质量分布信息构建可靠度指标，然后再依照可靠度指标进行推算解缠。在分块并行处理试验中，本文方法取得了较好的处理结果，处理效率较高。