临近冲击载荷的埋地聚乙烯燃气管道有限元分析

李茂东，陈国华，杨 波*，严大鹏，周池楼

(1.广州特种承压设备检测研究院，广州 510663；2.华南理工大学安全科学与工程研究所，广州 510640)

0 前言

聚乙烯管道因具有质量轻、成本低、耐腐蚀等优点被广泛应用于城市燃气输配管网系统。聚乙烯燃气管道首先是在欧美国家得到发展和推广应用，在20世纪80年代开始才在我国得到发展。我国目前已经建成的聚乙烯燃气管道约20×104km。聚乙烯燃气管道作为现代城市的“生命线”，分布在城市地下的角角落落，周边的人口、商业和企业众多，一旦发生事故，将直接影响到公众的生命及财产安全。随着城市建设迅猛发展，城市地下空间被不断开发利用，第三方施工如机械开挖、地表夯实、打桩等活动引发的燃气管道泄漏事故也随之而来，造成了重大的生命财产损失。在冲击作用区附近的埋地聚乙烯燃气管一旦发生管道应力集中、过大变形乃至破裂泄漏，极易引发严重事故[1]。分析2005—2016 年国内城市埋地燃气管道典型泄漏事故案例，统计结果如表1所示。在不完全统计的39起燃气管道事故种类统计中，第三方施工破坏占到了22起，其中比较典型的事故案例有2016年1月12日福州市站东路开挖电力沟过程中，挖掘机挖破站东路燃气中压聚乙烯管(DN200)，造成燃气泄漏，燃气漏损量约4 970 m3。2017年12月7日深圳地铁隧道遭打桩机打穿，而距离打桩点1 m多的地方埋有燃气管道。因此，有必要研究冲击载荷对附近埋地聚乙烯燃气管的影响，进而为聚乙烯管的安全运行提供科学合理的依据。

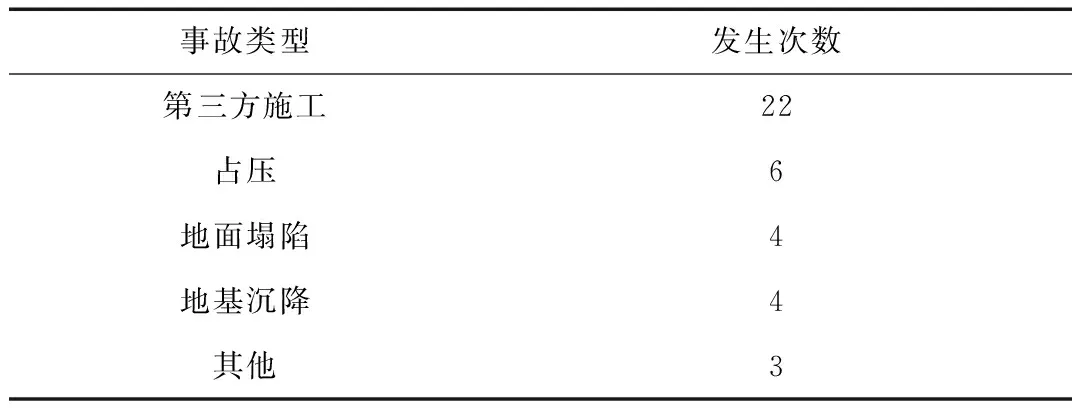
表1 燃气管道事故破坏类型及发生次数Tab.1 The type and frequency of accident damage of gas pipes

针对冲击载荷对埋地管道的影响，国内外学者进行了一些研究。Brooker[2-4]针对不同挖机斗齿参数、作用方式对钢管的损伤，进行了系列研究；Ryu等[5]通过试验和数值模拟研究了冲击载荷下腐蚀管道的变形；Wang[6]研究了地面撞击对核电站内埋地管道安全运行的影响；程梦鹏等[7]采用耦合欧拉 - 拉格朗日法，对承受挖掘载荷作用的钢丝缠绕增强塑料复合管(RTP)进行强度失效分析；周立国等[8]分析了挖掘载荷直接作用与未直接作用对聚乙烯管道的损伤状况影响；李军等[9]分析了聚乙烯燃气管道在挖掘齿作用下的力学响应及典型工况下的失效过程；韩传军等[10]建立了夯锤 - 管道 - 围土耦合三维模型，分析了夯击过程对钢制管道截面变形及所受冲击力的变化规律；佘艳华从地面施工振动的角度分析了冲击载荷下埋地钢管的动力响应，并对影响因素做了参数敏感性分析[11]。

目前针对冲击载荷作用下埋地聚乙烯管的研究，特别是对聚乙烯管偏移冲击作用区域的安全距离研究较少。因此，本文建立了冲击载荷下埋地聚乙烯管的管土相互作用模型，分析了冲击作用下聚乙烯管的材料模型、管道压力、土体性能、冲击速度、偏移冲击区域距离等对聚乙烯管力学性能的影响，为埋地聚乙烯管的铺设、防护、维护和安全运行提供科学依据。

1 模型建立

1.1 有限元模型

为简化计算，采用关于管道横截面对称的1/2长方体管土模型，对称面设置在有限元模型右侧。设定模型相关尺寸如下：土体宽度(W)为150 m，高度(H)为7.5 m，长度(L)为10 m。冲击块设置为圆柱体，半径(r)为0.5 m，高度(h)为0.5 m。聚乙烯管种类为PE80-SDR11，管径(D)为110 mm，壁厚(e)为10 mm，长度与土体长度一致。

根据规范《聚乙烯燃气管道工程技术规程》[12]，有限元模型设置聚乙烯管埋深为0.9 m，水平方向偏移冲击块正下方0.5 m。管道压力为0.4 MPa。将聚乙烯管按照正确位置装配后，选择六面体八结点网格单元(C3D8单元)，对管道和土体进行网格划分。考虑管 - 土相互作用接触处的复杂性及关键性，对管周局部土体进行网格细化，划分后的网格如图1所示。

图1 有限元模型Fig.1 The finite element model

1.2 载荷与边界条件

在有限元模型底部设置固定约束，在对称面施加对称约束。建立管土接触对，接触面设置为面对面接触，管道外表面为主面，土体与管接触面为从面。建立冲击块与土接触对，接触面设置为面对面接触，冲击块底部为主面，土体与冲击块接触面为从面。接触属性为有限滑移，允许管土间的相对滑动，管土之间摩擦因数为0.4[13]36。加载聚乙烯管压力为0.4 MPa以及重力加速度为9.8 m/s2，设置冲击速度为20 m/s，采用显式动力学(Dynamic，explicit)分析。

1.3 土体模型

冲击载荷通过管土相互作用传递到聚乙烯管上，在管 - 土相互作用下，管周土体既是作用在聚乙烯管道上的载荷，同时也挤压管道两侧，促使管道从变形中恢复，增强管道强度和刚度，对管道的变形起到一定保护作用[14]。选择Abaqus有限分析软件提供的扩展Drucker-Prager模型[15]。扩展Drucker-Prager模型由于在描述岩土等材料受力变形现象的准确性，在工程和研究中得到广泛认可。土体Drucker-Prager模型参数如表2[14]146、表3[14]146所示。

表2 土体Drucker-Prager模型参数Tab.2 Parameters of Drucker-Prager model of soil

表3 土体Drucker-Prager模型的硬化参数Tab.3 Hardening parameters of Drucker-Prager model of soil

注：(σ1-σ3)Tresea屈服准则。

1.4 聚乙烯管本构模型选择

为便于建模，不考虑管道系统的管件和连接件，假定聚乙烯管是各向同性材料。模型的长度和宽度足够大，可以用来模拟无限大的土体。

聚乙烯管材作为聚合物，自身的黏弹性使得材料的弹性模量随着时间的推移而减小。根据文献[8]，采用Prony级数模拟聚乙烯管道的黏弹性时，聚乙烯管道与时间相关的黏弹性参数如表4所示。聚乙烯管道的瞬时弹性模量为578.71 MPa。

表4 聚乙烯管道的黏弹性参数Tab.4 Viscoelastic parameters of PE pipes

根据文献[14]实验测得的应变率为10-5s-1时聚乙烯管材的本构模型，表达式为：

(1)

式中σ——聚乙烯管道的应力，MPa

ε——聚乙烯管道的应变

模拟所用聚乙烯管道材料的参数如表5[13]60所示。当采用Prony黏弹性模型时，埋地聚乙烯管道最大Mises应力为2.599 MPa。采用表5的本构模型时，计算得到的管道最大Mises应力为2.761 MPa。两者相比，采用应变率相关本构模型的模拟结果相对保守，在同样的安全系数下运行标准会降低。对于城市燃气管道，一旦发生泄漏，造成灾难性的事故后果，是社会和居民生活所不能接受的，因此在有限元模拟中选择使用基于应变率相关的本构模型，聚乙烯管道材料参数见表5。

表5 聚乙烯管道材料参数Tab.5 Material parameters of PE pipes

2 结果与讨论

以冲击速度为20 m/s，聚乙烯管道压力为0.4 MPa、埋深为0.9 m，且位于冲击正下方竖直方向一侧0.5 m为例，聚乙烯管道的最大Mises应力为2.761 MPa，最大椭圆度为1.8 %。根据文献[8]，PE80聚乙烯管的强度失效判据为8 MPa，应变失效极限为5 %，在模拟的工况下，聚乙烯管道没有发生损坏。因此，将进一步具体分析冲击载荷下影响参数对管道安全运行的影响。

2.1 冲击速度的影响分析

设置聚乙烯管道压力为0.4 MPa，位于冲击正下方竖直方向一侧0.5 m时，建立冲击速度分别为5、10、15、20、25、30、35、40 m/s的8个模型，聚乙烯管道最大应力基本保持不变。如图3所示。在冲击作用下，外部载荷通过土体传递给埋地聚乙烯管道，由于作用时间很短，冲击速度的改变对管道应力和变形没有较大的影响。由于冲击块半径为1.0 m，埋地聚乙烯管道此时仍然处于冲击作用区域内。建立埋地聚乙烯管位于冲击正下方竖直方向一侧1.5、2.0 m的2个模型，从图2可以看出，聚乙烯管道最大应力随冲击速度的改变而基本不变，而随着远离冲击作用区域而应力减小。

■—偏移正下方0.5 m □—偏移正下方1.5 m △—偏移正下方2.0 m图2 聚乙烯管道最大应力与冲击速度及偏移冲击区域距离变化的关系Fig.2 Von Mises of PE pipes vs speed of impact load and offset distance

从整体上看，聚乙烯管道没有发生明显变形，在短暂的冲击下，管道应力和变形都在安全极限之内，聚乙烯管道并没有发生破坏。建立埋地聚乙烯管道位于冲击正下方竖直方向一侧5.0 m的模型，聚乙烯管道的最大应力为2.757 MPa，应力进一步降低。

当聚乙烯管道仅承受内压时，根据文献[16]，规格为SDR11-DN110 的聚乙烯管道的理论最大Mises应力为：

(2)

式中pi——管道内压，MPa

k——外径与内径之比

代入数据，计算得到聚乙烯管道内压在0.4 MPa时，最大Mises应力为2.095 MPa。可知，在埋地状态下，聚乙烯管道最大应力主要来源于管道内压和土体压缩传递给聚乙烯管的外力。在冲击载荷下，由于冲击载荷作用时间较短，土体受到冲击块的撞击，向下挤压聚乙烯管道，管道的位移改变量较小。

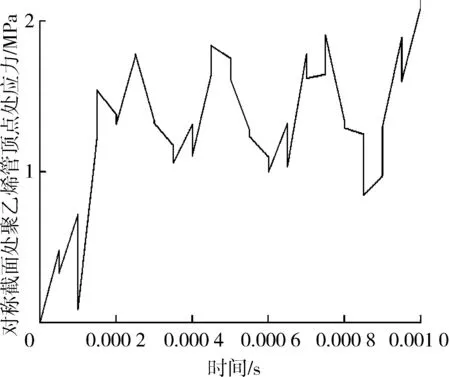
图3 对称截面聚乙烯管道顶点应力时间历程曲线Fig.3 Time history diagrams of Mises stress of PE pipes

取对称截面处聚乙烯管道顶点分析，其应力随时间历程曲线如图3所示。从图3可以看出，该点应力在0.000 2 s应力时达到峰值，之后一直在峰值作用上下波动。

2.2 土体弹性模量的影响分析

为研究覆土对埋地聚乙烯管的影响，设置聚乙烯管压力为0.4 MPa，位于冲击正下方竖直方向一侧0.5 m时，建立土体弹性模量分别为10、20、30、40、50 MPa的5个模型。图4是聚乙烯管最大Mises应力随土体弹性模量变化关系曲线。从图4可以看出，随着土体弹性模量增加，聚乙烯管的最大应力减小。说明在聚乙烯管埋深不变的情况下，符合标准的覆土对管道的安全运行十分有必要。图4也说明了在《城镇燃气输配工程施工及验收规范》[17]要求0.5 m以上的回填土进行压实处理的科学性。

图4 聚乙烯管道最大Mises应力随土体弹性模量的变化Fig.4 Von Mises of PE pipes vs elasticity of soil

2.3 管道内压的影响分析

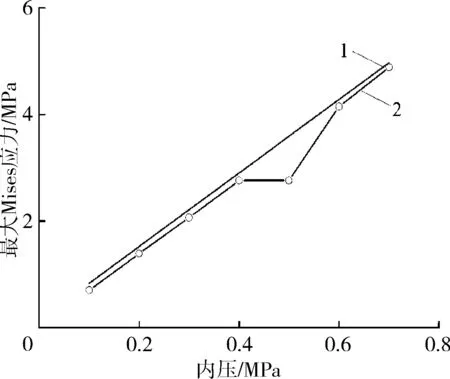
1—偏移正下方0.5 m 2—拟合图5 聚乙烯管道最大应力随着管道压力的变化Fig.5 Von Mises of PE pipes vs stress

从式(2)可以看到，聚乙烯管道载荷一部分来自管道内压的影响。当埋深为0.9 m、冲击速度为20 m/s时，设置聚乙烯管道内压为0.1、0.2、0.3、0.4、0.5、0.6、0.7 MPa共7个模型，聚乙烯管道的最大应力随着管道压力的变化如图5所示。从图5可以看出，聚乙烯管道最大Mises应力随着聚乙烯管道内压的增大而增大，近似成线性关系。

考虑聚乙烯管道远离冲击作用区域，设置偏移冲击正下方作用一侧为1.5、2.0 m。图6是聚乙烯管道最大应力随内压及偏移冲击区域的变化曲线。从图6可以看到，随着远离冲击区域，聚乙烯管道的最大应力随内压增加而增大的速度减慢，增大了管道运行的安全性。这说明在同样内压的情况下，受到冲击载荷时，距离冲击区域越近的聚乙烯管道越容易失效。因此在进行地面施工时，应该及时了解附近埋地管道的具体信息，做好安全防护措施。

□—偏移正下方1.5 m ■—偏移正下方2.0 m图6 聚乙烯管道最大应力随内压及偏移冲击区域的变化Fig.6 Von Mises of PE pipes vs stress and offset distance

2.4 偏移冲击作用区域距离的影响分析

冲击速度/m·s-1：□—10 ○—20 △—30 ■—40图7 聚乙烯管道最大应力随冲击速度和偏移距离的变化Fig.7 Von Mises of PE pipes vs speed of impact load and offset distance

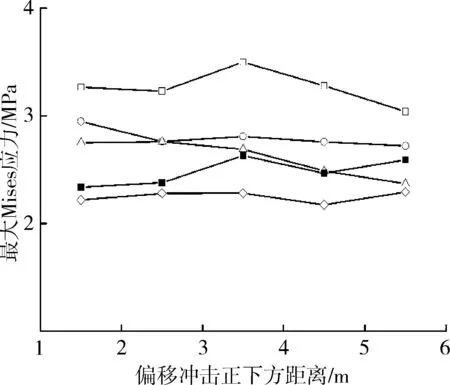
为研究在冲击载荷下，远离冲击区域对埋地聚乙烯管安全运行的作用，设置聚乙烯管偏移冲击正下方距离为1.5、2.5、3.5、4.5、5.5 m。图7是聚乙烯管道最大应力随着冲击速度和偏移距离的变化。从图7可以看到，由于冲击的作用，聚乙烯管道最大应力在远离作用区域的过程中，出现波动下降的趋势。从整体上来看，聚乙烯管道最大压力随着远离冲击作用区域而减小，冲击速度的改变没有对聚乙烯管道应力变化产生太大影响。当偏移距离达到5.5 m时，最大应力有明显的下降。《中华人民共和国石油天然气管道保护法》第三十条规定：“在管道线路中心线两侧各五米地域范围内，禁止使用机械工具进行挖掘施工等危害管道安全的行为”。因此，也说明施工区域与埋地管道保证规定的安全距离是非常有必要的。当在埋地管道附近进行地面施工作业的时候，一定要提前了解管道信息，在信息不明的情况下，及时探测，按照管道保护法要求与埋地聚乙烯管保持5.0 m以上安全距离。

图8是聚乙烯管道最大应力随着土体弹性模量和偏移距离的变化。从图8中可以看到随着土体弹性模量的增加，聚乙烯管道的最大应力减小。当土体弹性模量较小时，聚乙烯管道的最大应力随着远离冲击区域，出现波动后有明显减小的趋势。当土体弹性模量较大时，覆土已经有足够的保护作用，聚乙烯管道最大应力随着远离冲击作用区域没有明显的减小，即使距离冲击区域较近也会维持安全运行状态。

图9是聚乙烯管道最大应力随着管道内压和偏移距离的变化图，可以看到，当管道压力较大时，远离冲击作用区域可以减小聚乙烯管道最大应力。而当聚乙烯管道压力较小时，由于最大应力已经处于较低水平，改变偏移距离对聚乙烯管道的安全运行已经没有明显的改善效果。

土体弹性模量/MPa：◇—10 ○—20 △—30 ■—40 ◇—50 图8 聚乙烯管道最大应力随土弹性模量和偏移距离的变化Fig.8 Von Mises of PE pipes vs elasticity of soil and offset distance

PE管内压/MPa：◇—0.5 ■—0.4 △—0.3 ○—0.2 □—0.1图9 聚乙烯管道最大应力随着管道内压和偏移距离的变化Fig.9 Von Mises of PE pipes vs stress and offset distance

3 结论

(1)由于冲击作用时间较短，冲击造成的管道变形较小，管道没有发生明显的损伤，冲击速度对聚乙烯管道没有明显影响；

(2)按照施工规范进行回填土的压实处理，减小土壤之间的孔隙，增大土体的弹性模量，能够在管道和外部载荷之间发挥有效的屏蔽作用，减小地面载荷对管道的直接作用，可以对管道有明显的保护作用；

(3)聚乙烯管道最大应力随着聚乙烯管道内压的增大而增大，近似成线性关系；

(4)当管道压力、冲击速度等因素相同时，距离冲击区域越近的聚乙烯管越容易达到强度失效极限，而且聚乙烯管道最大应力随内压增加而增大的速度随着远离冲击作用区域而减缓。