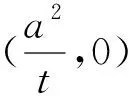2018年新课标Ⅰ卷理科数学第19题的研究与推广

安徽省宣城中学 (242000) 项卫华

众所周知,高考试题是命题专家集体智慧的结晶,一道好的试题不仅具有典型性,代表性,还具有进一步探索、研究的价值.本文对2018年高考数学新课标Ⅰ卷理科第19题进行了思考探究并做引申推广.

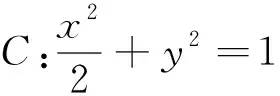
(1)当l与x轴垂直时，求直线AM的方程；

(2)设O为坐标原点，证明：∠OMA=∠OMB.

一见此题，笔者立即联想到下面两道高考试题：

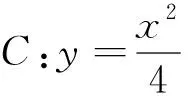
(Ⅰ)当k=0时，分别求C在点M和N处的切线方程；

(Ⅱ)y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由.

(2013年陕西卷理科第20题)已知动圆过定点A(4,0),且在y轴上截得的弦MN的长为8.

(Ⅰ)求动圆圆心的轨迹C的方程;

(Ⅱ)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点.

真可谓“年年岁岁花相似，年年岁岁题不同”，通过对上述试题的研究，笔者得到以下命题.

1.问题的一般化

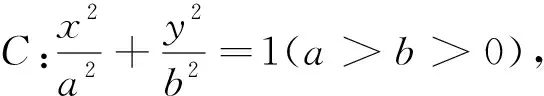
证明：设直线l:x=my+t(m≠0),M(x1,y1),N(x2,y2),联立直线l与椭圆C的方程得(a2+b2m2)y2+2b2mty+b2(t2-a2)=0,则y1+y2=

2.横向类比推广到抛物线、双曲线

命题2 已知抛物线C:y2=2px(p>0)，过定点(t,0)(t>0)且不垂直于x轴的直线l与抛物线C交于M,N两点，则在x轴上存在点P(-t,0)，使得∠OPM=∠OPN.

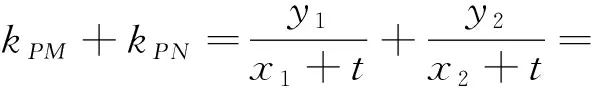
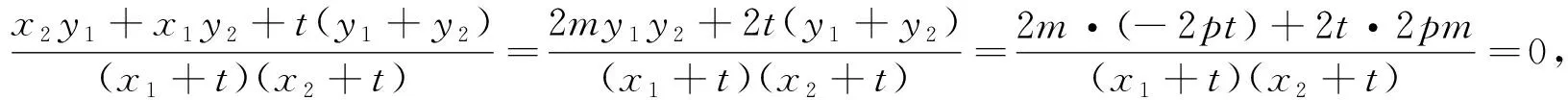
命题3的证明可仿照命题1、2的方法证得，此处不再赘述.

3.逆向思考变式探究

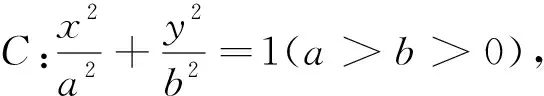
证明：设直线l:x=my+n(m≠0),M(x1,y1),N(x2,y2),联立直线l与椭圆C的方程得(a2+b2m2)y2+2b2mny+b2(n2-a2)=0,则y1+y2=

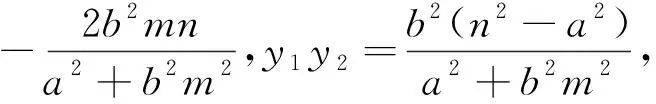
命题5 已知抛物线C:y2=2px(p>0)，点P(-t,0)(t>0)，设不垂直于x轴的直线l与抛物线C交于M,N两点，若∠OPM=∠OPN，则直线l过定点(t,0).

证明：设直线l:x=my+n(m≠0),M(x1,y1),N(x2,y2),联立直线l与抛物线C的方程得y2-2pmy-2pn=0,则y1+y2=2pm,y1y2=-2pn,

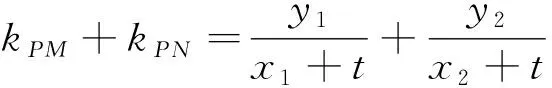
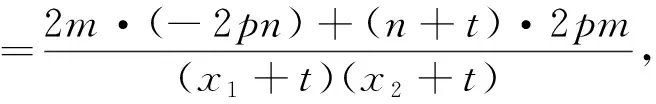
命题6的证明可仿照命题4、5的方法证得，此处也不再赘述.

由上述的命题1、2、3可以得到圆锥曲线中的一个等角定理：