不确定性需求下快速路应急疏散鲁棒优化模型*

何胜学

(上海理工大学管理学院 上海 200093)

0 引 言

作为交通网络“主动脉”的快速路在区域应急疏散中发挥着重要交通疏运作用.尽管存在大量的快速路管理控制优化研究，但是针对应急疏散情况下快速路优化管理的研究却非常有限.以最常用的匝道释放流量调节作为控制手段，本研究尝试针对不确定疏散需求条件下的快速路疏散有效控制进行研究.一般而言，疏散需求的不确定性表现为对于一个指定疏散起点，仅可知其在指定时段内的疏散流量上下限和可行疏散期内总的疏散需求，而没有其他相关信息，例如，需求的随机分布规律.疏散需求的不确定性不仅会给快速路的优化控制建模带来不便，也会造成无法对所建模型进行有效求解的困难.

So等[1]提出了一种上游优先的快速路疏散自适应式控制策略，利用该策略不仅可以在最短时间完成疏散，而且不需要疏散需求的具体信息.但是该策略假设快速路主线车流的行驶速度为无限大，任何一个匝道的到达车流率均大于近邻下游的主线分段临界流率，而上述假设与现实明显不符.本研究借鉴了文献[2]中快速路的拓扑结构，即不考虑下匝道分流且疏散仅有一个下游目的地.Zhang等[3]针对无起讫点对需求信息的快速路控制进行了研究，给出了一个两阶段控制策略.尽管对需求信息没有要求，但是该研究假设所有下匝道与下游出口具有稳定的交通流率.细致分析可知上述两研究给出的方法在本质上是相同的.与上述两个研究的假设相仿，本研究假定确切的动态交通需求是不可得的.何胜学[4]将文献[1]给出的方法进行了拓展，给出前向树状紧急疏散网络的自适应式控制策略.

在确定性静态交通流量条件下，Wattleworth[5]最早利用线性规划技术建立了一个高峰期的快速路控制模型.基于元胞传播模型(CTM)，Ziliaskopoulos[6]给出了一个以系统最优为目标且仅有一个终点的动态交通流分配模型.同样基于CTM, Chiu等[7]研究了一般紧急疏散网络的管理问题.文献[2]通过对高阶宏观交通流模型的修正，给出了如何利用地面辅道缓冲疏散车流的快速路优化控制方法.尽管上述方法可以对快速路交通流演变进行较细致的刻画，但是实际应用时需要对大量的网络元素进行细分，并对各种路网参变量进行标定与输入，因此，并不适用于不确定性需求条件下的快速路紧急疏散分析.特别是在给出控制方案的时间要求紧，且各种前期数据缺乏情况下，上述建模方法的劣势更加突出.本研究将基于上述考虑，在合理的假设条件下，寻求更加简单有效的建模方法.

为了处理不确定的动态疏散需求，本研究将利用仿射可调节的鲁棒优化方法.该方法是由Bental等[8]首先提出的，在网络和交通运输方面的应用可参阅文献[9-13].以CTM作为建模基础，Bental等[14-15]利用该方法对动态交通分配和物流网络中的不确定需求进行了分析研究.上述已有研究为本研究提供了可借鉴的思路.

1 确定需求下的基础疏散模型

1.1 主要参变量

图1为条用于紧急疏散的快速路.假设危险源处于快速路的上游端口附近，而避难所处于快速路的下游端口附近，所有匝道均有车辆需要紧急疏散.为了区分各匝道疏散风险的差异，在随后的模型中将给出相应的风险权重.

带箭头的短斜线-上匝道；带箭头的水平线-快速路分段.图1 紧急疏散中的一条快速路

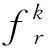
1.2 基本假设条件

应急疏散期间的交通管理与控制在许多方面有别于日常的交通管理与控制.①快速路疏散有一个可行的疏散时间期.从各上游匝道进入快速路主线的疏散车流一般具有共同的开始时间；②快速路疏散交通流一般具有单向和共同目的地的特征；③为了使疏散车流通畅快捷的通过主线，在各个主线分段的车流始终不允许超过最大临界交通流率；④来自各匝道的疏散需求一般是不确定的.假设仅可以估计出各匝道处的总疏散需求上限，以及各个分时段的需求大致变化范围.

假设主线分段遵循图2所示的交通流基本关系图，则任何时段的主线分段流率将小于临界流量qCr.如果当前分段的流率为qAB，那么其可对应的交通流状态包括自由流状态A和拥挤状态B.在相同的时间段内，两个状态下通过分段的车辆总数相同；但是当处于拥挤状态B时，所有通过的车辆将花费更长的时间并体验令人不悦的交通拥挤.如果在疏散过程中始终保持主线的交通流率低于临界流率，则交通状态将维持在自由流状态.这样既避免了对复杂多变的拥挤状态进行管理控制的必要，也保证了疏散车流运行的平顺快捷.

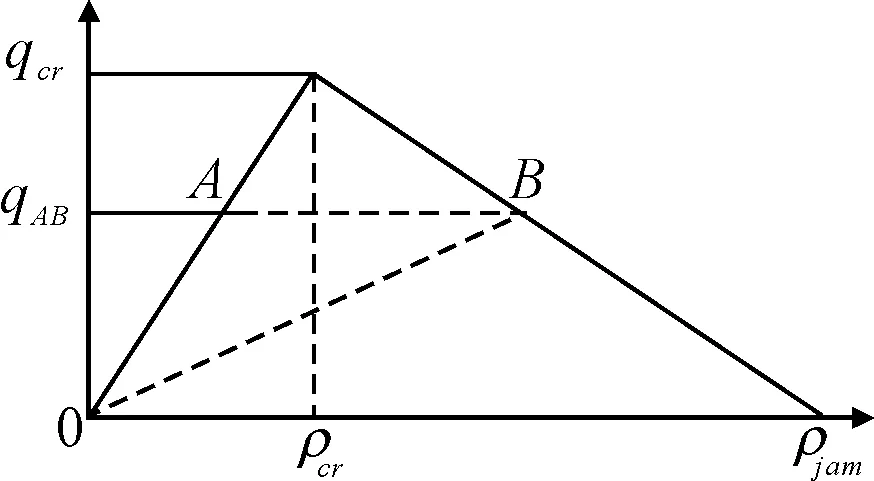
图2 三角形流量-密度-速度基本关系图

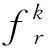
1.3 快速路基础疏散模型

1.3.1等价的目标函数

基于主线车流维持自由流状态的假设，易知在疏散车辆进入快速路后，其到达下游目的地的时间确定.因此如果各匝道处总的实际疏散车辆数给定，则总的车辆行驶时间为定值.综上，疏散优化目标应考虑最小化所有疏散车辆在匝道处等待被加载进入主线的时间.

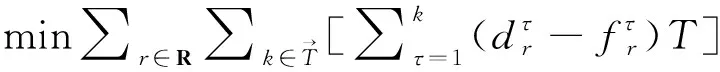
图3 具有动态需求的快速路假想累计 到达与释放流量曲线

1.3.2基础模型

基于已有的假设条件，建立相应的快速路疏散基础模型为

(1)

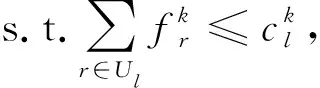
(2)

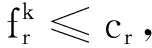
(3)

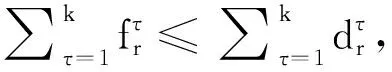
(4)

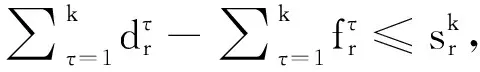
(5)

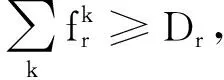
(6)

(7)

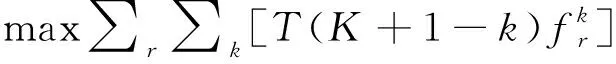
2 考虑不确定需求的鲁棒优化模型

2.1 不确定的动态疏散需求

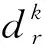
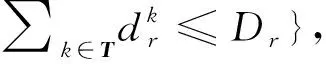
(8)

用θ表示疏散需求的不确定性水平，则式(8)可等价表示为

(9)

在基础疏散模型MP1中加入约束条件(8)或(9)，模型将变为一个难以处理的半无限维数学规划问题.如果没有进一步的处理，很难得到新模型的最优解，有时甚至很难得到一个可行解.

2.2 鲁棒优化模型

(10)

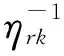
MP2:minz

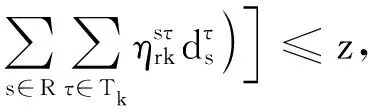
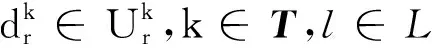
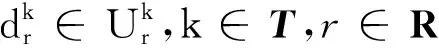
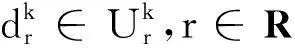
(11)

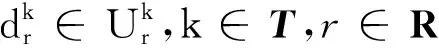
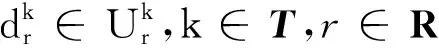
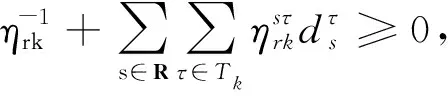
MP2仍然是一个难以处理的半无限维优化问题.但是可以利用线性规划的强对偶理论对MP2相关约束进行处理，得到如下一个等价的可处理线性规划模型：

MP3:minz

∀τ∈T,s∈R

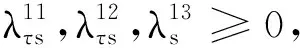
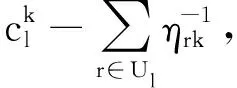
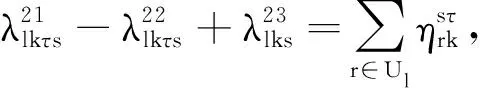
s∈R,k∈T,l∈L

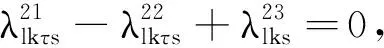
s∈R,k∈T,l∈L

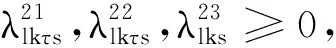
s∈R,k∈T,l∈L

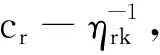
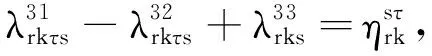
s∈R,k∈T,r∈R

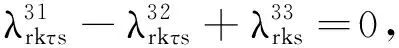
s∈R,k∈T,r∈R

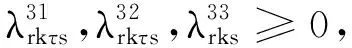
s∈R,k∈T,r∈R

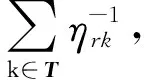
∀τ∈T,s∈R,r∈R

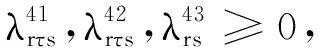
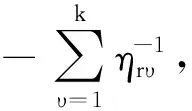
∀τ∈T,s∈R,k∈T,r∈R

s∈R,k∈T,r∈R

∀τ∈T,s∈R,k∈T,r∈R

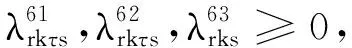
s∈R,k∈T,r∈R

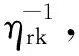
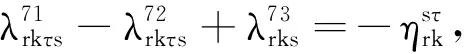
s∈R,k∈T,r∈R

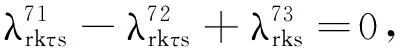
s∈R,k∈T,r∈R

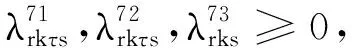
s∈R,k∈T,r∈R

(12)

上述模型MP3中，λ表示对偶变量集合，增加的相关数字上标是为了简化参变量表述.I(s)定义为一个0-1变量.当条件s满足时，I(s)=1；否则，I(s)=0.

证明.利用下面的关系式，可将所有受不确定数据影响的约束转变为一个等价的线性问题：

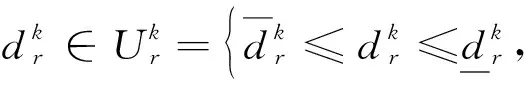
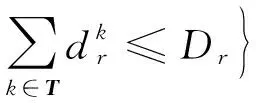
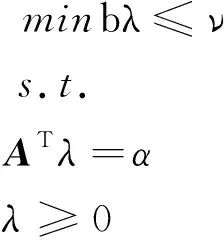
因此，存在满足bλ≤ν,ATλ=α和λ≥0的对偶变量λ，定理得证.

尽管MP3的规模相比于MP2明显增大，但是由于该模型仍然为线性模型，因此，可以利用已有的商业软件高效求解.本文随后的算例分析部分将采用数值优化软件Lingo13.0，该软件具有非常好的线性规划求解效率.例如在处理近30 000个变量和13 000个约束的算例时，得到最优结果仅需数秒，因此本文不再对模型的求解算法加以展开分析.

3 算例分析

以一条与图1具有相似拓扑结构且包含5个上匝道的快速路为例，该快速路的基本数据见表1.

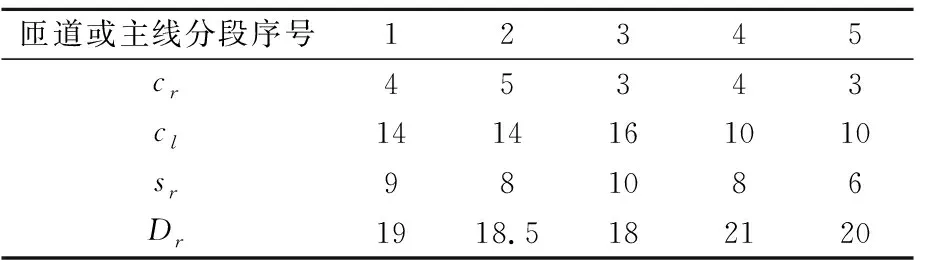
表1 快速路疏散系统的基本参量

为了简化分析，设定所有匝道的疏散优先权权重均为1，且所有匝道具有相同的多面体式疏散需求约束形式.令K=10，并假设所有疏散车辆与kT=5T时段前全部抵达相应的匝道处.在以上假设条件下，模型MP3共包含29 482个变量和13 057个约束.

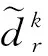
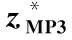
表2 不确定性水平与名义需求大小对的影响

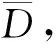
在利用SSP求解带有不确定性需求的MP1模型时，假设疏散需求服从指定的Beta分布.首先利用随机生成的50个样本计算SSP方法的指导性释放疏散车流和最终优化目标值；随后，分别利用MP3和SSP对1 000个需求样本进行疏散处理，并将疏散结果的目标均值和最差的目标函数值加以比较.表3为需求服从Beta(1,1)、名义需求为3.6以及cp=-5的比较结果；而表4为需求服从Beta(2,5)、名义需求为3.2以及cp=-20的比较结果.

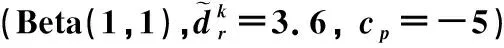
表3 MP3与SSP的疏散效果比较

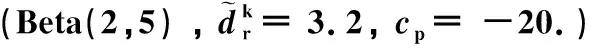
表4 MP3与SSP的疏散效果比较

由表3～4可知，SSP方法所得目标函数值在不同的不确定性需求水平下均高于MP3的计算结果.这一现象合理反映了两种方法的本质特征.SSP的目标函数值是对已知样本计算的一种均值；而MP3给出的是最糟糕情景下可行疏散方法的结果.用两种方法对1 000个随机样本进行实际处理，表3～4中的数据显示利用MP3的方法在样本目标均值方面优于SSP.利用MP3的方法所得样本目标值波动范围较小，即对应的标准方差较小.在对1000个随机样本处理中的最糟糕情景下，MP3的表现则更加出色.利用MP3的方法不仅能保障解的可行性，而且提供了目标函数值的下界；而SSP则不具有上述两方面的优势.

4 结 束 语

快速路应急疏散具有不同于日常交通的一些特征，因此有必要针对这些特征实施有效的疏散管理与控制.应急疏散的一个突出特征就是疏散需求信息的不确定性.以上匝道作为快速路疏散的起点，疏散管理者往往只能估计不同时段到达各上匝道的疏散车流上下限和可行疏散期内总的疏散车流，而没有其他关于疏散需求的信息.据此建立的疏散优化模型具有不可处理的半无限维特征.针对上述问题，在假设到达车流与匝道释放车流之间存在仿射关系条件下，利用线性规划的强对偶条件将半无限维模型转化为等价的一般化模型，从而实现对不确定需求的有效处理.通过与随机抽样规划方法的比较，说明本研究所给出的鲁棒优化方法的合理性与有效性.

尽管通过在模型中添加权重系数考虑了疏散优先权，但是本文并没有对此展开深入分析.疏散优先权对疏散整体效果的影响和优先权的合理分配可以作为一个拓展研究方向.本研究假设主线车流维持自由流状态，但是可能的一些意外可能导致该假设失效，因此有必要针对如何处理该类现象加以研究.