道路平面线形拟合方法比较研究*

张 航 韦金君 张肖磊

(武汉理工大学交通学院 武汉 430063)

0 引 言

公路平曲线线形逐桩坐标可以通过GPS或全站仪等测量仪器测量获得.但是如何利用测得的数据获取平曲线的设计参数，一直困扰着道路设计者[1].尤其在改建旧路的工程中，由于道路长期使用产生疲劳徐变或由施工原因造成旧路的边坡垮塌、地基塌缩、路基沉降[2]等，都可导致道路线形实际数据与原设计参数有差别.为获取平面线形参数，一方面设计者基于CAD技术，用短小线段来拟合曲线，使曲线尽量的贴合原有数据，最后逐段读取线形参数，这种方法既不能保障曲线的光滑性，也带有很强的主观性；若使用CAD样条曲线或圆弧段来拟合曲线，虽然满足了曲线光滑性，但拟合精度更是取决于原有数据的多少.另一方面，为达到拟合平面线形的精度，充分利用道路中线坐标数据，专家学者们应用拉格朗日插值法、最小二乘法、三次样条法及路线设计软件等方法[3-5]，分别就曲线拟合原理及结果进行讨论，至于哪种方法更适宜以及哪种成果的拟合精度更高，缺乏针对性的研究和提炼.基于此，本文基于上述方法并结合工程实例，基于数值分析理论，应用Matlab软件讨论平面线形的拟合成果及精度，得出适宜的拟合方法，为道路线形拟合技术推广以及改扩建工程线形参数获取提供依据.

1 平面线形拟合

1.1 路线线形曲率

道路平面线形由直线、缓和曲线和圆曲线组成.文献[6]规定，平曲线半径不宜大于10 000 m，故当曲率κ≤0.000 1 m-1时，可认为此时曲线为直线，故设置平面线形中直线与曲线点曲率误差.

当采样点曲率κ≤0±ε时，点在直线上；当采样点曲率κ=C±ε(C=1/R为定值)时，点在圆曲线上；当采样点曲率0±ε≤κ≤C±ε时，采样点在缓和曲线上.由于路线曲率连续变化，主点位置可按曲率定值间插值得到.

各测量点的曲率：

(1)

式中：y′为测量点的一阶导数；y″为二阶导数

1.2 曲线线形参数

圆曲线半径计算值由曲线曲率κ计算所得：

R=1/κ

(2)

曲线转角：

θ=arctanki-arctanki-1

(3)

式中：k为该点斜率.

缓和曲线参数：

(4)

式中：Ls为缓和曲线长.

缓和曲线长度与横纵坐标关系：

(5)

(6)

式中：x0，y0为缓和曲线终点坐标.

2 平曲线拟合实例

将分别采用拉格朗日插值法、最小二乘法、三次样条曲线和纬地路线设计软件等四种方法，以S型平曲线(两个基本型首尾反向相接)为例，对道路线形中常见的S形道路路线进行拟合，最后综合分析各自拟合成果及效果.

例中，曲线转角α1=53°09′46.2″,α2=28°08′59.7″，圆曲线半径R1=330 m，R2=350 m，缓和曲线长度Ls1=150 m，Ls2=90 m，平曲线各分段为：直线段1K0+000—K0+054.260，缓和段2K0+054.260—K0+204.260，圆曲线段3K0+204.260—K0+360.456，缓和段4K0+360.456—K0+510.456，直线段5K0+510.456—K0+515.216，缓和曲线段6 K0+515.216—K0+605.216，圆曲线段7K0+605.216—K0+687.174，缓和曲线段8K0+687.174—K0+777.174，直线段9K0+777.174—K0+808.143.

2.1 拉格朗日插值法

在拉格朗日插值法拟合中，由于数据较多或者间隔不均匀等原因可能造成拟合曲线节点之间的插值函数与原数据有较大误差，使得拟合出的多项式为高次多项式，在拟合曲线中部能够较好拟合，而在两端出现较大摆动，即出现龙格现象[7].为了防止龙格现象出现，减小拟合误差，将曲线分为五段拟合.输入各段样点数据，可拟合得出函数表达式为：直线段1(K0+000—K0+054.260)：y=-0.505 1x+453.557 5

缓和段2(K0+054.260—K0+204.260)：

y=0.000 59x4-0.25x3+66.38x2-10 370.47x+719 635.14

圆曲线段3(K0+204.260—K0+360.456)：为了对比在圆曲线段拟合由龙格现象引起的误差，拟合采用圆曲线段全部样点数据输入拟合与中部部分点拟合方法进行对比.

方法①：由圆曲线11个点拟合：y=

0.00 089x4-0.39x3+113.65x2-19 419.56x+1 491 192

方法②：由圆曲线中部5个点拟合：y=0.010 9x2-2.104 9x+529.727 6

方法③：由圆曲线中部4个点拟合：y=

-0.001 6x2+2.432 2x-500.778 0

由拟合函数可知：方法①拟合不符合圆曲线函数特点，可直接舍去；方法②、方法③分别由式(2)计算得到R1=331.550 m，R2=712.18 m，可见方法③误差过大.由此看出，方法②拟合结果符合要求.

缓和段4(K0+360.456—K0+510.456)：

y=-0.03x3+13.73x2-3531.17x+395 320.79

直线段5(K0+510.456—K0+515.216)：

y=-0.49x+843.14

同理，拟合缓和段6(K0+515.216—K0+605.216)、圆曲线段7(K0+605.216—K0+687.174)，缓和段8(K0+687.174—K0+777.174)，直线段9(K0+777.714—K0+808.143)，分别得出缓和段、圆曲线段、直线段表达式，由式(2)，计算得到R2=350.25 m.

由直线段1，5，7 拟合表达式与式(3)，得到路线偏角：α1=53.1 628 389 114°,α2=28.151 464 805°.路线拟合段曲率见图1.

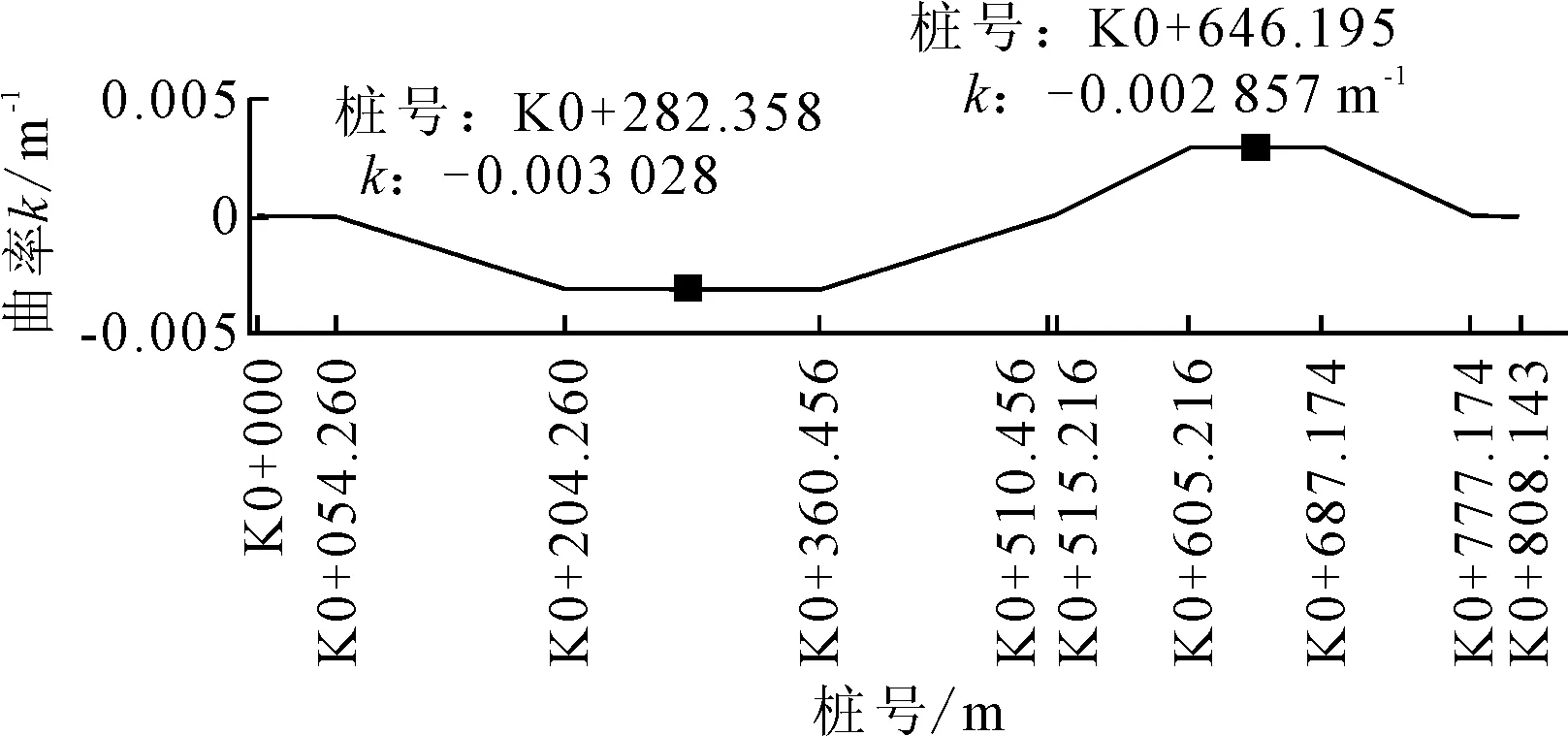
图1 拉格朗日拟合法拟合曲线曲率

2.2 最小二乘法

最小二乘法拟合道路线形是指在拟合曲线整个长度范围内，拟合样点距离拟合曲线的垂直距离的方差总和达到最小值时，此曲线为最小二乘法拟合的最佳曲线.为便于计算曲线参数，对各段进行分段拟合：

①对K0+000—K0+054.260、K0+510.456—K0+515.216、K0+777.714—K0+808.143段：

直线段1：y=0.51x+74.97

直线段2、3：y=-0.49x+843.14，y=0.03x+260.31

直线段拟合出的曲线都为一次函数，由式(3)可得：α1=53.1 628 389°，α2=28.1 499 232 °

②K0+204.260—K0+360.456、K0+605.216—K0+687.174段为圆曲线：

圆曲线1：y=-0.001 537x2+2.37x-488.04；

圆曲线2：y=0.001 534x2-3.62x+2 440.71；

由式(2)得，R1=330.03 m，R2=353.355 769 m；

③K0+054.260—K0+204.260， K0+360.456—K0+510.456， K0+515.216—K0+605.216， K0+687.174—K0+777.174段为缓和曲线段,拟合曲线分别为：

缓和段1.y=0.006 521x2-3.01x+707.64.

缓和段2.y=-0.000 954x2+1.34x-35.23.

……

各分段函数拟合曲线的曲率图见图2.

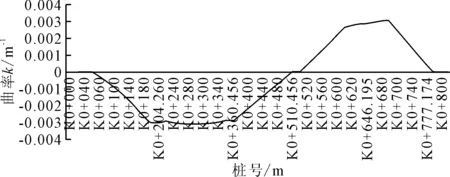
图2 最小二乘法拟合曲线曲率图

2.3 三次样条曲线

三次样条曲线在全区间[a,b]上都有连续一、二阶导数，具备描述公路基本线形特征[8].圆弧样条曲线只有一阶导数，没有二阶连续导数，三次样条曲线整条曲线二阶连续.输入个桩号的X、Y坐标，得到各段三次样条曲线表达式及三次样条拟合图，三次样条曲线表达式为

S(x)=a(x-x1)3+b(x-x1)2+

c(x-x1)+d

(7)

得到各分段表达式后，为更为直观的表现拟合结果，绘制三次样条拟合曲率图，见图3.

由图3可知，整条曲线的拟合有可识别的特征点(主点)，判断主点由每两个点的三次多项式函数式(7)来计算每个样点处的曲率，由曲率反推出此点的半径，若计算得出某段范围内的曲率小于等于10-5，那么这段就可认为拟合出的样条曲线为直线段，在某一段的曲率近似为一个固定的相差不大的值，那这段就可认为是圆曲线段，这两者之间拟合出来的曲率为按定比渐变的一段即缓和曲线段，由此判断出主点位置.并通过计算每段的参数特征得出曲线的整体参数.

由式(2)～(3)可求得圆曲线各参数如下：R1=330.248 947 m，R2=350.220 040 m，α1=53.1 628 551°，α2=28.1 499 46°.

2.4 纬地路线软件拟合

纬地道路设计软件拟合时，使得各个散点尽可能的分布在拟合曲线上，由此得出路线的线形参数.这种方法有很大的主观性，在拟合过程中需要不断试算、修改，操作起来较为复杂，对设计人员的专业知识和工作经验有很高的要求.优点在于线形拟合出来后直接得到线形参数，减少了对数据进行编辑整理的工作量及编辑整理过程中可能出现的误差.纬地道路软件拟合成果见图4.

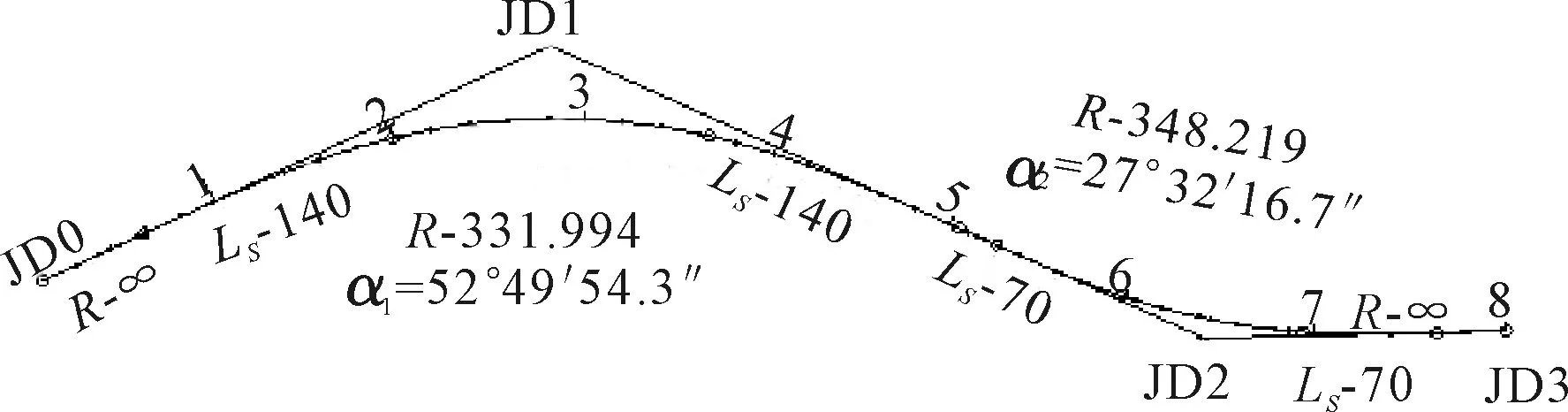
图4 纬地软件拟合曲线图(R,L 单位：m)

由图4可知，并不是每个点都精确地在曲线上，特别是圆曲线部分尤为明显.使用纬地软件拟合输出的线形参数：R1=331.994 204 m，R2=348.218 918 m，α1=52°49′54.3″，α2=27°32′16.7″，Ls1=148 m，Ls2=85 m.

3 拟合方法分析

3.1 拟合原理对比

1) 三次样条曲线 曲线拟合时，每相邻两个测量数据点均用三次曲线连接，保证了函数表达式二阶可导，相邻一阶连续.三次样条函数的二阶导数为一次函数，与回旋曲线曲率变化特点相符；当拟合圆曲线时，曲率为一定值；当拟合直线时，曲率为0.该方法强调点必须在曲线上，即道路中线上.

3) 拉格朗日插值法 拉格朗日插值法是指通过已知样本点，考虑通过n+1个点的n次插值多项式存在且唯一，按照线性插值、抛物线插值顺推至一般情形的一种多项式插值方法.随着次数的增加，拟合函数通过所有样本点，但可能在拟合曲线端部产生较为强烈的波动曲线.

4) 纬地路线设计软件拟合法 纬地软件拟合是在排除粗差点后，利用已知散点数据在纬地道路辅助设计软件中逐一输入并调整路线参数，使得拟合线条贴合数据点，从而得到拟合路线.

3.2 拟合特征分析

1) 拟合曲线光顺性 由图1～4可知，三次样条和纬地路线软件的拟合效果较为显著，也最符合曲线连续并光滑的要求；拉格朗日插值法因龙格现象在分段曲线边缘处的拟合误差影响了曲线的整体光滑平顺；最小二乘法也出现在分段点处的曲率过渡不良，整体的平顺性和曲率渐变性也差.

2) 拟合曲线保真性 对应用于道路改扩建工程的情况，设计要求新建道路尽可能与原路重合.拉格朗日插值法和最小二乘法得到的曲线均不能很好的保持原有曲线的性质；三次样条曲线能最大限度还原旧路线形；纬地路线软件的拟合难以保证所有测量点吻合在中线上，曲线易失真.

3.3 拟合结果比较

整理上例拟合结果，见表1.

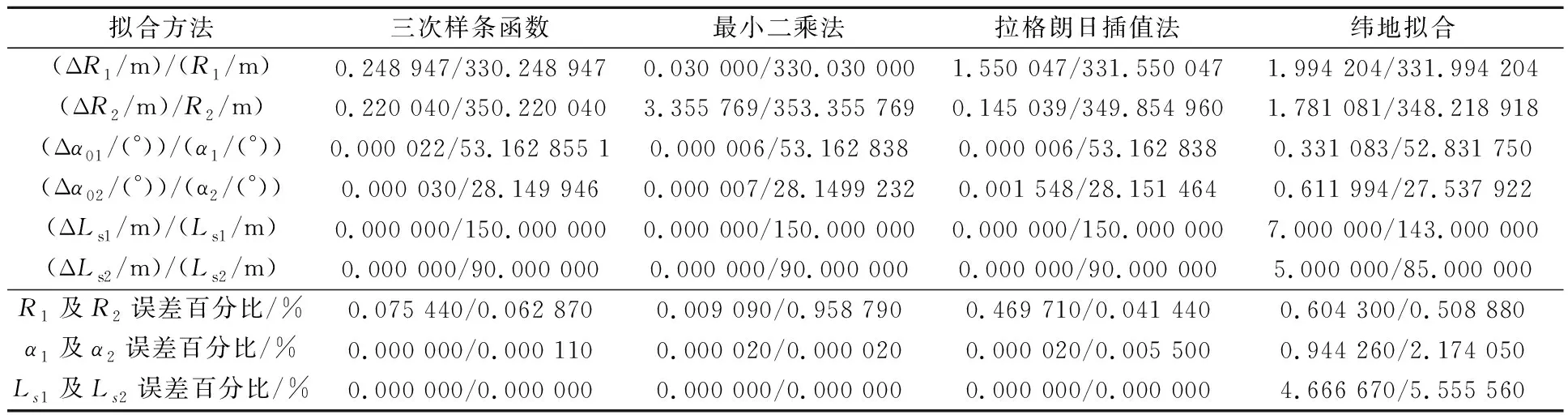
表1 几种拟合方法计算结果比较

由表1可知，拉格朗日法用单一的曲线拟合道路平曲线，将平曲线三要素用一个表达式表示，拟合误差较大；最小二乘法对平曲线进行分段拟合，直线段拟合结果误差较小，曲线半径误差较大；三次样条曲线拟合时，表达式简洁而且误差较小，纬地道路软件拟合可能出现多种拟合结果，误差多样性大.

综上所述，三次样条函数拟合结果最好，而纬地拟合误差最大.

4 工程实例

某省道干线公路，设计速度80 km/h，双向2车道，由于途径煤矿产地，货车通行量大，超载现象严重，自建成通车，行车时常冲撞中央分隔带及防护带危及行车安全，使得在剧增的交通需求量下交通事故频发.综上，考虑公路现状及运行安全，需要对现有路线进行改扩建.因施工年代较早，道路原有设计资料与现有情况不符，因此在改扩建之前，需获取道路中线参数，采用GPS与全站仪相结合按桩距20 m对道路中线坐标进行测量；另外在事故多发路段、曲线段等处加测坐标点，对平面线形选用三次样条拟合.某弯道测量拟合结果见表2.

根据各个曲率变化范围推算出线形参数.

由表2可知：

表2 三次样条拟合各段参数特征

1) 拟合段(541.696,1 299.992)～(540.645,1 304.311)，(564.001,1 652.549)～(586.461,1 711.310)为直线段，由(3)式得出，该曲线的偏角为34.725 471 23°.

2) 拟合段(519.202,1 417.743)～(532.334,1 560.809)为圆曲线段，各端点曲率取平均值，由式(2)算出，该弯道半径为404.044 m.

3) 拟合段(540.645,1 304.311)～(519.202,1 417.743)、(532.334,1 560.809)～(564.001，1 652.549)为缓和段，由式(5)、式(6)有，缓和段长度为LS=118.003 81 m.

5 结 论

1) 讨论了拉格朗日插值法、最小二乘法、三次样条曲线及纬地软件等几种拟合方法的应用原理，并结合实例分别进行拟合计算，得出三次样条曲线较其它方法具有精度高和光滑性好等优势.

2) 工程实例表明，三次样条曲线拟合改扩建道路，设计线形达到了预期目的，利用原路段的中线吻合较好，部分线形需改善的路段，获取了相应的参数，保证了整个线形的平顺、流畅.

3) 样条曲线拟合的曲率个别出现跳跃情形，这与中桩步长取值及外业实施测量时的误差有关.因此，未来可以着力解决适宜的步长值在拟合平面线形时出现曲率方面的问题,达到曲率光顺性和正确性，力使三次样条曲线在改扩建工程中平面线形设计中得到充分应用.