带异步相关噪声的战斗机蛇形机动跟踪算法
卢春光,周中良,刘宏强,寇添,杨远志
空军工程大学 航空工程学院,西安 710038
蛇形机动是战斗机飞行员在隐蔽接敌、机动规避及协同探测等战术动作中经常采用的战术机动类型。在一定的空战态势下,飞行员进行蛇形机动反映了其战术意图,因此在空战中如何快速而又准确地识别出目标的蛇形机动模式对于明确其战术意图以及评估当前的战场态势具有十分重要的意义。目前,机动模式的识别主要从机动模式的几何特征(宏观)以及运动参量特征(微观)两个方面着手:文献[1]通过将战术机动进行分割并按时间序列进行编码,采用隐马尔科夫模型进行训练、识别;文献[2]通过提取目标航向角变化率、高度变化率等运动参量特征,设计了一个两级识别方案,采用模糊推理和时间自动机方法实现了机动模式的识别。对于蛇形机动目标而言,转弯角速度是其最为关键的运动参量,因此通过载机雷达的量测数据精确辨识出转弯角速度对于提高战斗机蛇形机动模式的识别率具有重要意义。
目前,机动目标转弯角速度辨识的问题已经得到了许多学者的关注。Roth[3]、Arasaratnam[4]、Jia等[5]、Huang[6]等将转弯角速度作为额外的状态变量,从而对状态进行扩维处理,分别使用扩展卡尔曼滤波/无迹卡尔曼滤波、容积卡尔曼滤波、基于5阶球径容积规则的高阶容积卡尔曼滤波、高阶鲁棒容积卡尔曼滤波等非线性滤波方法辨识角速度和估计状态变量。缺点是角速度估计的精度依赖于目标初始状态及协方差、过程噪声和量测噪声等因素;黄伟平等[7]、Zhu和Cheng[8]、Efe和Atherton[9]分别根据转弯角速度与目标速度方向角、速度、加速度之间的物理关系,首先采用非线性滤波算法估计出目标速度方向角、速度、加速度等状态量,而后间接辨识出转弯角速度。Yuan等[10]通过引入距离变化率量测,采用Cmin方法[11]并结合航向角的变化估计出两个可能的转弯角速度的值,基于此设计包含匀速模型和两个匀速转弯模型的交互多模型算法进行状态估计。Frencl等[12]通过引入距离变化率量测估计转弯角速度,并根据速度矢量在距离方向上的投影与距离变化率估计量之间的差异,对转弯角速度进行进一步修正以提高估计精度,然后依据最优线性无偏估计准则,利用粒子滤波进行状态估计。缺点是没有考虑角速度与目标状态之间相互耦合关系,增大了辨识风险;Bar等[13]通过采用匀速模型和扩维的匀速转弯模型设计了交互多模型算法,用于估计转弯角速度。缺点是辨识与估计精度依赖于模型切换概率与转移概率的设置;Yuan等[14]提出了基于期望最大化(EM)算法的转弯角速度辨识算法,该算法采取的是“先辨识-后估计”的策略,通过辨识出的转弯角速度进而估计目标的运动状态,缺点是依赖于初始值以及机动初始概率的设置。
在实际空战中,非合作目标的转弯角速度是未知且时变的,并且与目标状态相互耦合、彼此影响,一方面目标状态估计性能的提升有利于转弯角速度的辨识,另一方面转弯角速度辨识性能的提升有利于目标状态估计精度的提高。上述文献中所提到的转弯角速度辨识方法均没有考虑转弯角速度与目标状态之间的耦合关系以及这种耦合关系所带来的影响,并且均采取的是开环序贯处理方式,没有形成闭环反馈。而且上述文献所提到的状态估计与转弯角速度辨识方法中,都需要假设量测噪声与过程噪声是相互独立的,但是在实际跟踪过程中,这种假设条件往往难以满足,比如雷达在跟踪目标时,受目标运动速度以及观测角度的影响,导致过程噪声与量测噪声之间的相关性不能被忽略[15-16];在异步多传感器信息融合过程中,由于量测值作为输出反馈传递给网络系统,同样有可能使得量测噪声与过程噪声具有异步相关性[16-17];在自动目标识别系统和自动威胁识别系统中,当量测噪声和过程噪声同时依赖于系统状态时,传感器噪声与过程噪声之间也可能会存在相关性[18];同时由于连续系统离散化过程中,系统状态离散化采样时将引入额外的噪声到量测模型中,导致量测噪声与过程噪声之间存在一定的时空相关性[19]。因此,在联合状态估计和角速度辨识的过程中必须考虑这种相关性。噪声相关条件下的估计问题可以分为两大类:同步相关和异步相关。针对噪声同步相关条件下的状态估计主要有以下3种框架:噪声解耦框架、高斯近似递归滤波框架和相关高斯近似滤波框架。这3种框架对线性系统或者在最小均方误差意义下的非线性系统而言是等价的[20]。Bar[13]、Chang[21]、Hu[22]等采用重构伪状态方程的方式,来达到相关噪声解耦的目的,并分别设计了扩展卡尔曼滤波、边缘化的无迹卡尔曼滤波和无迹卡尔曼滤波进行状态估计;Wang等[23]通过计算两步状态后验预测概率密度函数和一步量测后验预测概率密度函数,基于二阶Stirling插值,设计了新的中心差分滤波器;Huang等[24]通过分析上述两种框架的缺点,设计了一种新的相关高斯近似滤波框架。针对噪声异步相关条件下的状态估计的研究主要有:于浛等[17]针对随机时滞和异步相关噪声情况,提出了一种改进的高斯近似滤波算法;Souto和Ishihara[15]针对异步相关噪声条件下的估计问题设计了一种鲁棒扩展卡尔曼滤波算法。
针对上述问题,本文通过将状态估计与转弯角速度辨识联合考虑,基于EM算法框架提出一种带异步相关噪声的联合估计与辨识算法,该算法通过解除目标状态与转弯角速度之间的耦合关系,进而获得转弯角速度闭环形式的解析解,并引入滑窗思想,以提高辨识的实时性,主要包括E-step和M-step 2个部分:E-step基于当前估计的角速度并利用带异步相关噪声的高斯近似滤波器与平滑器获得的后验平滑概率密度和联合分布密度,近似计算完整的对数函数似然函数的期望;M-step通过使期望最大化更新获得下一次迭代的角速度估计量。
1 问题描述
蛇形机动可以分解成若干个具有不同转弯角速度的圆弧转弯机动,因此蛇形机动目标转弯角速度的辨识问题相应地转化为圆弧转弯机动的角速度辨识问题。在带异步相关噪声背景下,假设目标在二维平面中运动,转弯机动模型状态方程及量测方程为
xk+1=fk(xk,Ωk)+wk
(1)
zk+1=hk+1(xk+1)+vk+1
(2)
式中:
fk(xk,Ωk)=
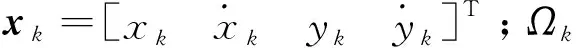
1.1 基于系统重构的角速度解耦策略
由于蛇形机动目标的转弯角速度Ωk这一未知参数非线性耦合在状态转移矩阵之中,传统的辨识算法仅能获得转弯角速度的近似解,辨识效果不佳,因此为了获取转弯角速度的解析解,就需要将转弯角速度与状态转移矩阵之间的非线性耦合关系解除,即在原有系统模型的基础之上,通过模型的转换,重构一个新的状态方程,将转弯角速度从状态转移矩阵中提取出来,从而解除这种耦合性,如式(3)所示:
xk+ 1=F(xk)θ+xk+wk
(3)
式中:
θ3=1-cos(ΩkT)
θ4=sin(ΩkT)

1.2 基于量测重构的异步相关噪声解耦策略
由于在上述异步相关噪声条件下,传统的高斯近似滤波器性能不佳,甚至发散,进而影响EM算法的辨识效果,所以为了实现状态的精确估计和转弯角速度的准确辨识,本节通过采用“去相关框架”[25],基于原有的量测模型,对量测模型进行转换,从而重构一个伪量测方程,使得重构的伪量测方程满足过程噪声与量测噪声之间的相关性解除。在重构的伪量测基础之上实现滤波和平滑,获得后验平滑概率密度和联合分布密度,进而实现转弯角速度辨识与状态估计。
在量测方程式(2)右边形式地加上一等于零的项:
fk(xk,Ωk)-wk)
(4)
式中:Gk+1为待定矩阵。
记
fk(xk,Ωk))
(5)
(6)
则量测方程转换成为
(7)
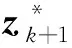
(8)
E[(vk+1-Gk+1wk)(vk+1-Gk+1wk)Τ]=
(9)
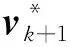
(10)
可得
(11)
(12)
2 基于HCKS-EM的联合估计与辨识算法
基于极大似然估计准则[26-27],本文提出了一种带异步相关噪声的联合状态估计与角速度辨识算法,具体的算法框架如图1所示。在第t次迭代时,利用带异步相关噪声的高斯近似滤波器与平滑器,获得目标状态的平滑估计量,并采用EM算法进行参数θ的辨识,辨识后的参数θ用于第t+1次的状态估计,不断迭代直到满足设定的要求为止。

图1 联合估计与辨识Fig.1 Joint estimation and identification
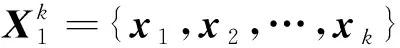
(13)
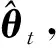
(14)
式中:
(15)
(16)
(17)
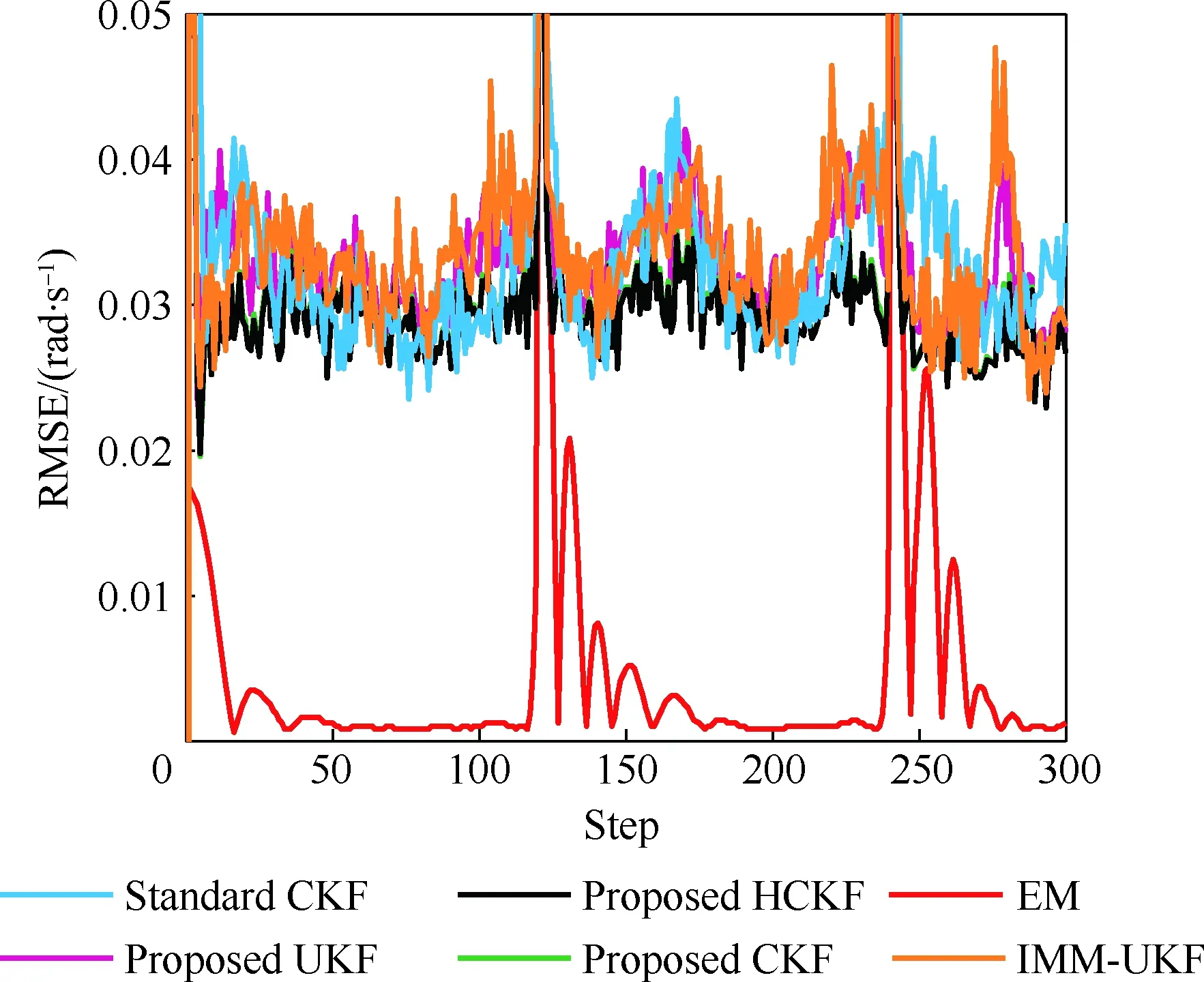
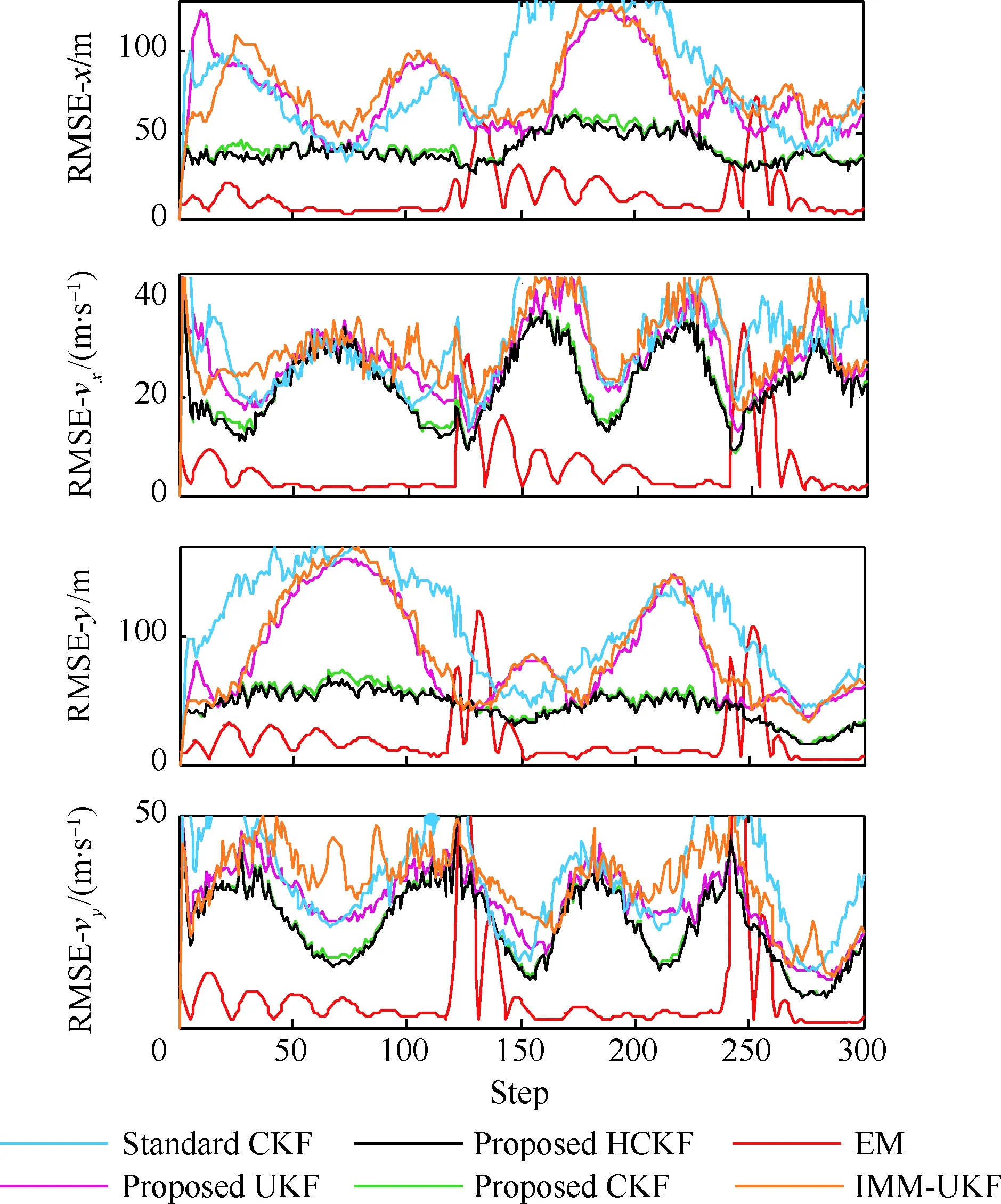
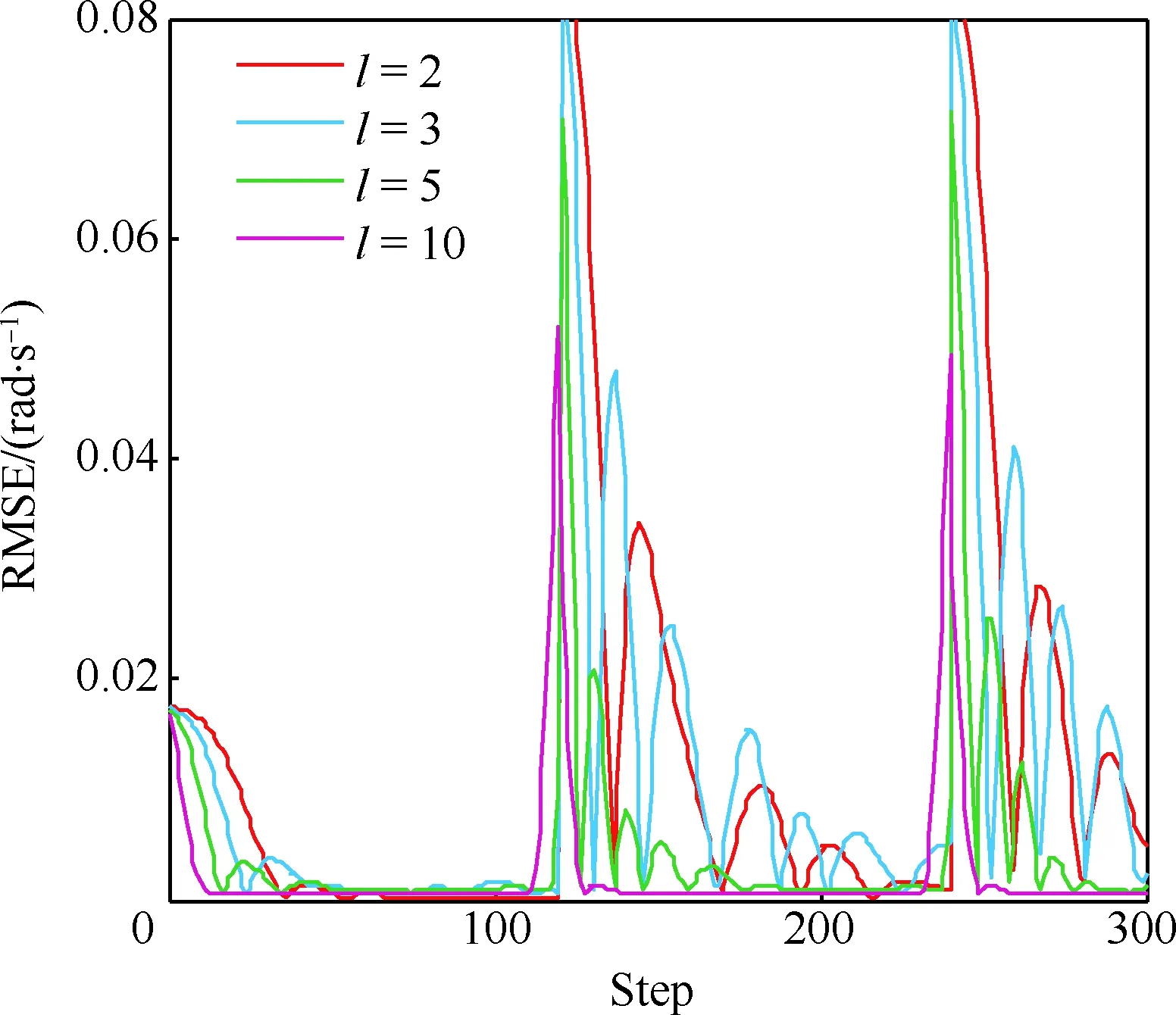
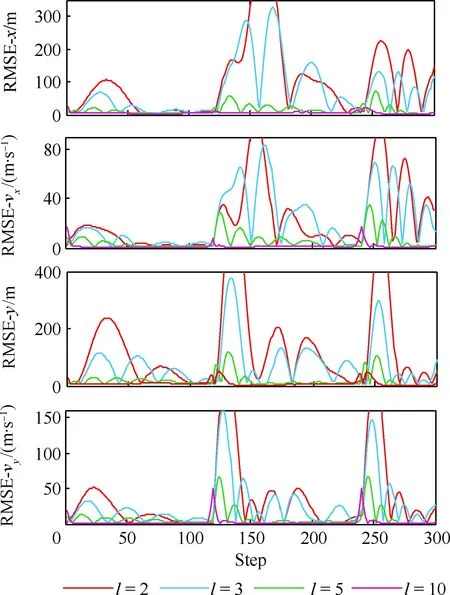
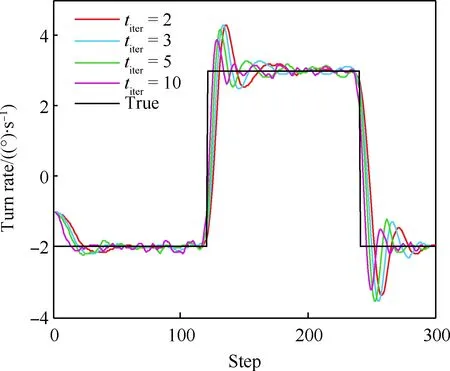
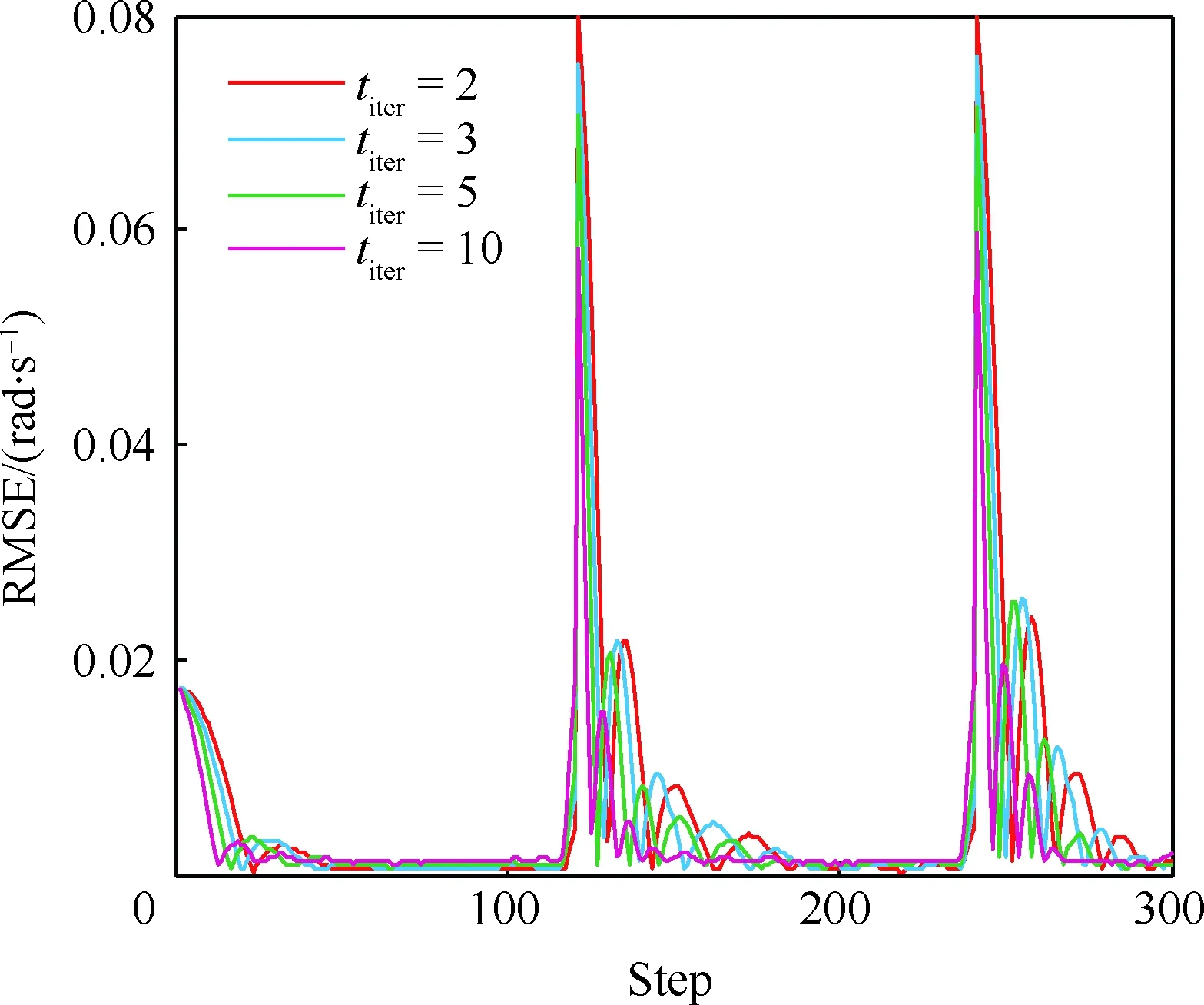
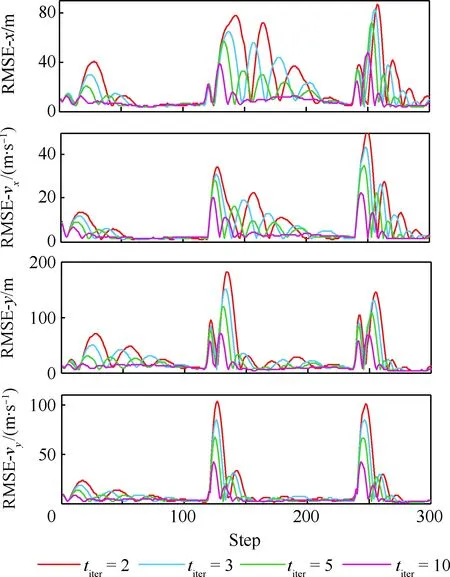
当l=k-1时,I1是一个常数,与待辨识量θ无关;当0≤l pθ(xk-i|xk-i-1)~N(xk-i;F(xk-i-1)θ+xk-i-1,Q) (18) (19) 跟据贝叶斯准则得到xk-i和xk-i-1的联合概率密度分布: (20) 采用带异步相关噪声的HCKS平滑器得到平滑概率密度时,将基于以下假设: 服从高斯分布[29]。 (21) 式中: 则 (22) (23) (24) (25) 将式(21)和式(23)代入(20)的联合分布,有 (26) 到k-i-1时刻的平滑分布为 (27) (28) (29) 为了求解I2,首先定义如下两种积分函数: (30) Δ(xk-i,xk-i-1)=∬F(xk-i-1)TQ-1(xk-i-xk-i-1)· (31) 然后分别将F(xi)、xi按xi的分量进行分解: (32) (33) (34) (35) 则 (36) (37) 本文采用Jia等提出的五阶球面径向容积规则[5]解决带异步相关噪声的高斯近似滤波器和平滑器中的非线性高斯积分的计算问题。基于容积规则的高斯积分求解可抽象成为 (38) (39) 式中:ej为空间Rn中的单位向量,其第j个元素为1;权值ws1和ws2分别为 (40) (41) 由矩匹配法可知,五阶径向规则当中,容积点与权重需要满足: (42) (43) (44) 将式(39)、式(43)和式(44)代入式(38)可得 (45) 由式(45)可知五阶容积规则的采样点数量为 2n2+1。 M-step的主要任务是解决I2的极大化问题,即求解使I2满足极大值时所对应的θt+1值,用于EM算法的下一次迭代更新: (46) 当I2取得极大值时满足: (47) 则可求得参数θ的迭代表达式为 (48) 本文采用的是滞后窗口,即辨识k-l时刻的参数θ的值需要使用[k-l,k]时刻的量测,然后通过反解参数θ与参数Ω之间的函数关系,求得k-l时刻目标的转弯角速度的辨识结果。 本文算法总结如表1所示。 表1 基于HCKS-EM的联合估计与辨识算法 基于HCKS-EM的联合估计与辨识算法的收敛性受带异步相关噪声滤波算法的收敛性以及EM算法的收敛性两个方面的影响。 对于EM算法的收敛性而言,为了更好地说明该算法的收敛性,需要给出以下定理: ∀t=1,2,… (49) (50) 令 (51) (52) (53) (54) (55) 对于式(54)右边第二项而言,已知当x≥0时,满足:lnx≤x-1,则 (56) 同样从式(54)~式(56)可以看出 (57) 本文利用水平方向上的转弯机动非线性动态模型,仿真出一条蛇形机动轨迹。假设机动目标在1~120 s以Ω1=-2 (°)·s-1作转弯运动,在k=121 s时转弯角速度突变为Ω2=3 (°)·s-1作转弯运动,在k=241 s时转弯角速度突变为Ω2=-2 (°)·s-1作转弯运动,并持续到300 s。设置转弯角速度初始值为Ω0=-1 (°)·s-1,采样周期T=1,q1=0.1 m2/s3,wk为零均值高斯白噪声,其协方差为Q。 通过载机雷达可以获得目标与载机之间的相对距离r、方向角φ的信息,则可获得系统的非线性量测方程为 本文提出的联合估计与辨识算法和扩维法的初始状态以及协方差分别设置为 初始状态: 初始协方差: P0= diag(100 m2,10 m2·s-2,100 m2,10 m2·s-2) 扩维法初始状态: 扩维法协方差: 100 mrad/s) 为了评估分析本文提出算法的性能,首先将本文算法与传统的扩维法以及基于UKF的交多模型算法(IMM-UKF)[32]进行对比分析。IMM-UKF算法采用了标准维纳过程速度模型和扩维的匀速转弯模型两种机动模型,并且两种机动模型的状态和协方差的初始值以及量测噪声和过程噪声设置与上文保持一致。维纳过程速度模型的状态转移矩阵为F,量测矩阵为H,表达式分别为 IMM-UKF算法中模型之间的转移概率矩阵为Π,初始模型概率矩阵为μ,表达式分别为 本文提出的联合估计与辨识算法采用滑窗机制,窗口设置为5,最大迭代次数为5次,各执行100次蒙特卡罗仿真。图2和图3分别为上述3种 算法对角速度辨识和目标状态估计的效果,从图2和图3中可以看出,本文提出的联合估计与辨识算法在角速度辨识和目标状态估计上比传统的扩维法以及IMM-UKF算法误差小,精度高,这主要是因为本文提出的算法解除了角速度与状态方程之间的耦合关系,从而便于获得角速度辨识的解析解,并且,采用了闭环反馈的处理方式,通过反复的迭代不断修正角速度辨识与目标状态估计的误差,从而提高了辨识与估计的精度。而且从图2和图3中发现,基于IMM-UKF算法的角速度辨识和目标状态估计的均方根误差要比传统的扩维法大,这主要是因为交互多模型算法处理的是目标跟踪时发生的模型不匹配问题,但是本文设计的蛇形机动仿真采用的是单一的匀速转弯模型,所以交互多模型算法的优势并未体现出来,产生的辨识与估计效果不佳。从图中可进一步看出,在异步相关噪声背景下,带异步相关噪声的高斯近似滤波器的估计与辨识效果优于传统的标准的高斯近似滤波器,这主要是因为,本文所提到的带异步相关噪声的高斯近似滤波与平滑算法采用了“去相关”框架,通过重构伪量测方程,解除了量测噪声与过程噪声之间的相关性,在目标状态与量测相互独立的基础上设计的滤波算法显然性能优于传统的滤波算法,并从图中可看出高阶容积卡尔曼算法估计与辨识效果优于容积卡尔曼算法和无迹卡尔曼算法,尤其是在量测噪声和过程噪声增大时,这种优越性就越明显,但是相应的计算量就会增加,计算时间增大,主要是因为高阶容积卡尔曼算法的采样点数量高于容积卡尔曼算法和无迹卡尔曼算法。 图2 角速度辨识均方根误差Fig.2 RMSE of turn rate identification 图3 位置和速度估计均方根误差Fig.3 RMSE of position and velocity estimation 其次,从该算法的本身结构着手,对该算法进行评估分析。主要从窗长和迭代次数两个方面分析。采取滑动滞后窗口策略,窗口长度l分别设置为2、3、5、10,最大迭代次数均为5次,各执行100次蒙特卡罗仿真。从图4和图5中可以看出,随着窗口长度的增大,该算法收敛于真实值的时刻就越早,精度越高,当角速度发生突变时,对于突变的角速度反应也越快。并且从图6和表2可以看出,窗口长度越大,该算法估计的目标状态整体精度就越高,但是消耗的时间越长,这显然是时间与精度之间的“博弈”问题,从图中还可以进一步看出,当窗长大于5时,由窗长带来的精度效益不太明显,相反时间消耗问题更加突出。 图4 不同窗口长度下角速度辨识结果Fig.4 Identification result of turn rate with different window length 对于迭代次数而言,将窗口长度l设置为5,最大迭代次数titer分别设置为2、3、5、10,各执行100次蒙特卡罗仿真。从图7和图8中可以看出,随着迭代次数的增加,该算法在收敛于真实值的时刻就越早,并且对于角速度突变反应的也比较灵敏,角速度辨识的精度也越高。 图5 不同窗口长度下角速度辨识均方根误差Fig.5 RMSE of turn rate identification with different window length 图6 不同窗口下位置和速度估计均方根误差Fig.6 RMSE of position and velocity estimation with different window length 表2 计算k=37 s时的角速度和状态所耗费的时间 Table 2 Time cost for calculating turnrate and states at k=37 s 滑动窗口长度l=2l=3l=5l=10时间/s0.013 60.019 30.032 40.056 2 图7 不同迭代次数下角速度辨识结果Fig.7 Identification result of turn rate with different iterations 图8 不同迭代次数下角速度辨识的均方根误差Fig.8 RMSE of turn rate identification with different iterations 表3 计算k=47 s时的角速度和状态所耗费的时间 Table 3 Time cost for calculating turnrate and states at k=47 s 最大迭代次数titer=2titer=3titer=5titer=10时间/s0.010 30.016 30.026 40.054 2 图9 不同迭代次数下位置和速度估计均方根误差Fig.9 RMSE of position and velocity estimation with different iterations 从图9目标状态4个分量的RMSE可以看出,迭代次数越大,该算法估计的目标状态整体精度就越高,但是从表3显示的不同迭代次数下计算k=47 s时的角速度和状态所耗费的时间越大,性价比不高。尤其是当迭代次数大于5时,由迭代次数带来的精度效益远远比不上时间带来的损耗,降低该算法的实时性。 1) 在E-Step,采用系统重构角速度解耦策略解除了转弯角速度与状态转移矩阵之间的耦合特性,在此基础上将完备似然函数进行分解,从而将其转换成带参数θ的解析表达式,降低了由于状态扩维法扩维所带来的复杂性;通过采用量测重构噪声相关性解耦策略,解除过程噪声与量测噪声之间的异步相关耦合特性,基于贝叶斯框架,设计了带异步相关噪声的高斯近似滤波和平滑算法,并基于该算法获得了目标状态的平滑估计。 2) 在M-Step中,通过极大化完备似然函数求得转弯角速度闭环形式的解析解,降低了辨识风险,提高了状态估计精度。 3) 仿真实验表明,本文提出的联合估计与辨识算法性能优于传统的扩维法以及交互多模型算法。
2.1 E-step
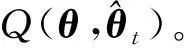
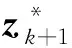
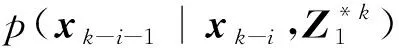
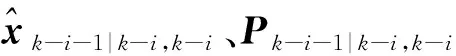
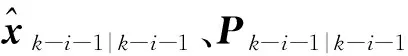
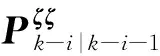
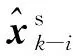
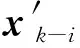
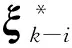
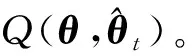
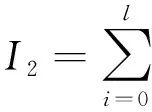
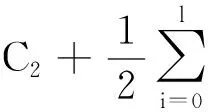
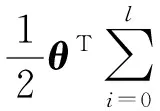
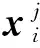
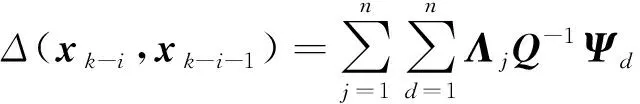

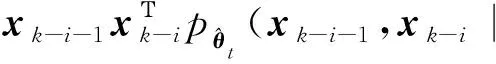
2.2 五阶球面-径向容积规则
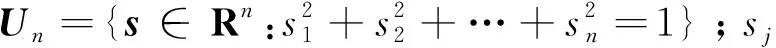
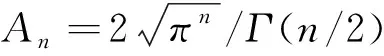
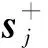
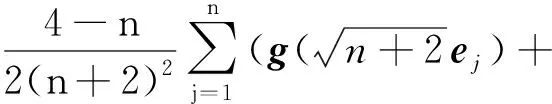
2.3 M-step

2.4 收敛性分析
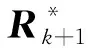
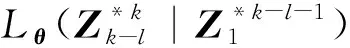
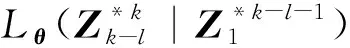
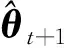
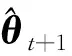
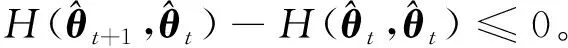

3 仿真分析
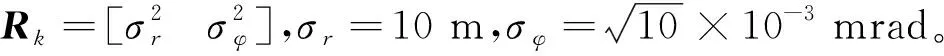
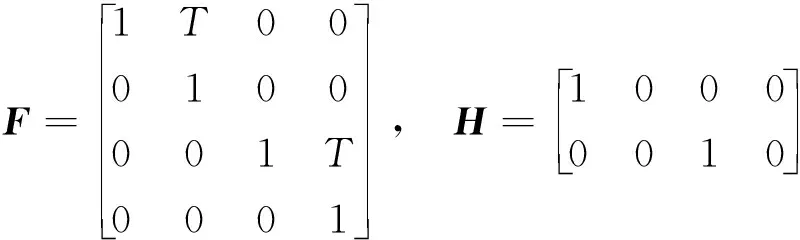
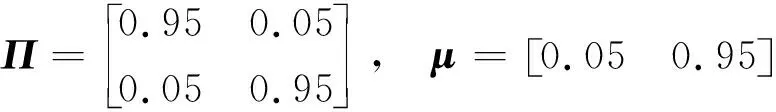

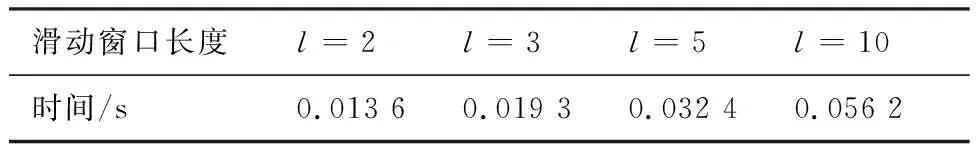

4 结 论

