嵌入式平台上的三维重建算法研究

蒋 林，郭 晨，朱志超，程文凯

1 引言

随着科学技术的发展，二维图像包含的信息已不能满足人们的需要，因此对真实场景的三维重建越来越受到广大学者的关注。在三维重建中机器人位姿的实时精确估计主要依靠轮式里程计、惯性测量单元、全球定位系统和视觉里程计等[1]。视觉里程计是其中重要的一种位姿估计方法。文献[2]提出了一种基于光一致性假设的视觉里程计方法（DVO，densevisual odometry）提高了位姿估计的精度和鲁棒性。文献[3]借鉴立体视觉里程计流程设计了一套基于Kinect的视觉里程计系统（FOVIS，fast odometry from vision）仅利用深度信息对相机位姿进行快速估计。文献[4]提出了一种帧到模型的视觉里程计方法（FOV，fast visual odometry），实现了数据集和模型集的快速配准。

然而，现有的三维重建中视觉里程计的算法主要在PC机上运行。虽然在PC机上已经获得较好的结果[5]，但是当这些算法移植到嵌入式平台后，效果就不太理想或者无法实现功能。随着机器人技术的发展，越来越多的三维重建需要在嵌入式平台进行实现。

利用移动机器人搭载的视觉传感器获取序列图像并进行提取特征点，然后对不同运动方式下获取的特征点分别采用不同的算法进行处理，简化移动机器人平台的位姿算法，可以降低计算量并同时满足精度要求。通过离线数据集进行离线实验和真实环境的机器人在线实验验证了提出的位姿估计方法的有效性。

2 移动机器人的运动和几何关系分析

2.1 室内机器人工作环境和运动方式的简化

基于视觉的三维建模中，相邻帧之间的位姿估计传统方法为：首先计算基础矩阵，然后根据基础矩阵求解本质矩阵，最后（SVD）奇异值分解本质矩阵[6]得到位姿转换矩阵，或者通过点云的PnP匹配[7]，得到近似位姿转换矩阵。并且已经出现了很多改进的算法，虽然在PC机上能实现实时的三维重建，但是计算量相对于嵌入式平台来说依旧较大、计算时间较长，严重影响三维建模在嵌入式平台的的实时性和精度。为了提满足在嵌入式平台的实时性和建模精度，通过分析室内环境建模的机器人运动方式的独特性，进而在不同的运动方式下采用不同算法，降低计算的复杂度提高建模的实时性。

日常生活中的运动方式有多种，例如三个维度上的平移、旋转、平移加旋转，运动分析较为复杂。但是通过对室内工作的机器人工作环境以及机器人的驱动方式进行分析后，发现室内移动机器人工作方式可以大大简化，平移只能在XOZ平面，旋转也无法在三个维度进行，仅仅只能绕Y轴进行，因此机器人运动时位姿转换矩阵也可以相应简化。

2.2 机器人与目标物体数学模型及几何关系

基础矩阵F是摄像机对极几何关系[8]的代数表达。对极几何示意图，如图1所示。摄像机在两个时刻（t1，t2两时刻成像中心不同）摄取具有一定相关性的目标图像，根据t1，t2时刻摄像机对应点关系，基础矩阵给出t1、t2时刻摄像机对的几何关系。

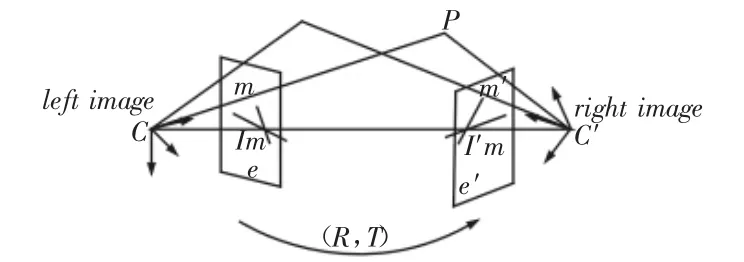
图1 对极几何示意图Fig.1 The Epipolar Geometry Diagram

本质矩阵是归一化的基础矩阵，由对极几何关系可知，基础矩阵与本质矩阵满足，如式[9]（1）～式（3）所示。

式中：F、E—基础矩阵和本质矩阵；Mr—摄像头标定后的内参数矩阵；［T］x—平移矢量T的反对称矩阵；R—旋转矩阵。

由式（3）可知，本质矩阵包含了摄像机的外参数R和T。本质矩阵可以通过式（2）求得，在对摄像头进行标定后内参矩阵即为已知。

3 机器人位姿估计

3.1 直线行走时位姿估计

通常在对运动物体进行位姿分析时要同时考虑旋转和平移，但是经过上文的对机器人平台的驱动进行分析后可知，轮式差动驱动在运动时不会同时发生旋转和平移，因此在位姿估计计算时就可以分别对旋转和平移进行分析，降低了分析和计算难度。

当两轮直线行走时，由室内机器人的工作环境和两轮的工作方式可知此时，此时只用求出Z方向上的位移参数tz就可以获得位姿转换矩阵。提出一种简化的计算参数tz的方法，可以减少计算量和获得满意的精度。

tz的计算流程：

（1）根据加速版的具有鲁棒性的特征算法SURF[10]（Speeded Up Robust Features）提取特征点。

（2）对特征点进行匹配，并对匹配后的距离进行阈值判断，对距离小于一定阈值的特征点对进行保留。

（3）根据保留下来的特征点找到点云中相对应点，并对点云中的该点做可信度判别。利用拉普拉斯四邻域算子对点云中对应的点的深度值做卷积，保留卷积结果为0的点，这些点就是点云中更加可信的点。然后获取可信点的深度值Zi，求所有可信点深度值的平均值

（4）令 tz=Zmean，求得 tz。

如果邻域系统是4邻域，Laplacian算子的模板为：

表1 4邻域模板Tab.1 Template of 4 Neighbourhood

上述的计算流程第二步是为了获得更高的匹配准确度，第三步使用拉普拉斯4邻域算子对特征点相应的点云中的点进行检测，检查该点是否处在一个平坦的平面上。由于有些特征点在第二步判断中虽然有一个很小的距离值，但是该点在三维环境中可能处在一个尖锐物体的角点，这时因为存在测量误差，并且无法判断该点误差值。因此为了避免选取这样的点，使用Laplacian算子模板做卷积，并且留下做卷积后结果为0的点，这样可以使处在平坦物体平面上的特征点被保留，tz的结果也更加精确。因为直线运动时位姿转换矩阵中只有一个未知参数tz，当tz通过上文计算得到后，位姿转换矩阵就确定了。

3.2 转弯时位姿估计

转向时的位姿估计精度要求更高，为了提高位姿估计的精度，利用SURF进行特征点提取和匹配，并且对匹配后的特征点进行一系列的处理。通过对描述符的相似度阈值和对特征点Y轴坐标进行限制，可以选择出更好的匹配点。

差动式驱动的移动机器人两轮的运动可知，理论上机器人平台在转弯时不存在平移，只绕着Y轴旋转，旋转矩阵R=，但是由于运动误差依旧会产生微量平移，平移矢量此时E可表示为：

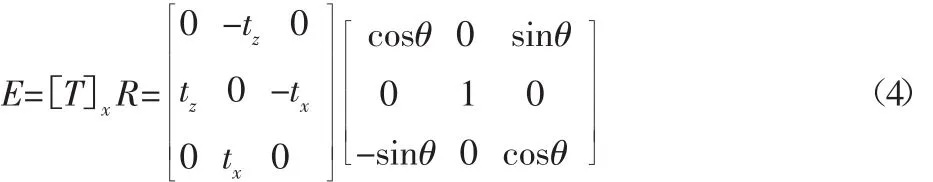
式中：［T］x—t时刻机器人坐标系到t′时刻机器人坐标系的平移矢量T=［tx0 tz］T的反对称矩阵；R—对应的旋转矩阵。

通过将式（4）展开并且整理可得式（5）～式（7）：

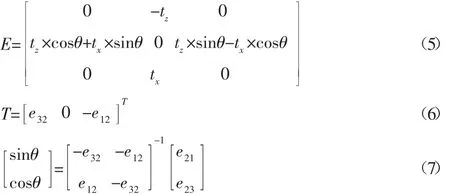
将式（7）中的参数代入R中，旋转向量R和平移矢量T可直接获得结果，此时可以得到旋转是的位姿转换矩阵。与其它方法相比，本小节的算法大大减少了计算的复杂度，并且R和T唯一，保证了对机器人姿态控制。

4 实验研究

为了验证方法的有效性，在室内环境下进行实时三维重建实验。实验平台为ARM9主控器嵌入式平台，摄像头为Kinect 1.0。不同方法下的特征点匹配结果，如图2、图3所示。多种方法在三维重建时计算位姿转换矩阵的时间对比，如图4所示。在线实现效果图，如图5所示。通过kinect采集转弯时的两帧图片利用SURF特征点匹配后的结果，如图2所示。通过上图可知，由于环境复杂存在大量误匹配点。对图2显示的匹配特征点进行筛选后的结果的匹配结果，如图3所示。筛选条件为：当特征点的特征向量的欧式距离小于阈值和两帧图像特征点的Y轴坐标应相同。这两个条件同时满足时该特征点才能够满足我们的需求。这里的算法、PnP算法和ICP算法的计算时间对比图，如图4所示。从图4中明显可看出相比传统的算法这里的算法时间更少。

图2 原始SURF特征点提取匹配结果Fig.2 Matching Results of Original SURF Feature Point

图3 两帧图像的匹配结果Fig.3 Matching Results of Two Frames of Images

图5 在线实验结果Fig5 The Online Experimental Result

真实实验环境下进行的实时三维重建，如图5所示。从图5中可看出转角部分没有重影，基本满足重建模型精度需求。实际测量值的绝对误差图，如图6所示。绝对误差的大小与测量距离成正比关系，但是关键帧的选取将对测量值进行阈值限制，保证绝对误差在较小的范围内。当移动机器人平台直线运动时，平移矢量T的参数tz的估计值与实际值依旧存在误差.图中横坐标表示实际移动距离，纵坐标表示绝对误差。此处要注意的是“实际值”其实并非真正的“真实值”，因为这个“实际值”也是通过测量得到的，这个测量精度要比Kinect的测量精度高很多，所以可以将此“实际值”当做真实值。

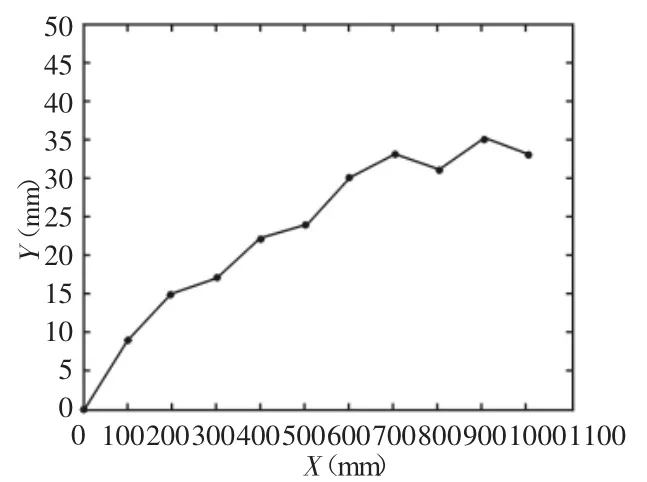
图6 实际测量值的绝对误差图Fig.6 The Absolute Error of the Actual Measured Value

5 结论

提出的将复杂运动简化为同一时刻仅存在平移或者旋转，然后分别对这两种情况用不同的方法求解转换矩阵，简化了转换矩阵的求解过程，降低了计算量，使基于视觉的实时三维重建在嵌入式平台上得到实现。基于真实环境下的机器人在线实验验证了所提出的转换矩阵求解方法的有效性和优越性。但是依旧存在一些问题，随着机器人的移动，转换矩阵的误差会逐渐累积，最后会影响重建结果，因此后续需要做回环检测和图优化，以获得更加精准的重建效果。