平板式催化剂装箱过程中轨迹规划的研究

许 超，邹光明，王兴东，王 黎

1 引言

高阶轨迹规划主要应用在工业机器人、精密机床、微机械等高精密设备中，与二阶梯形速度曲线相比，其运动曲线更加平滑，稳定性大大增加，能够使设备运动中的冲击性和残余振动极大地减小[1-2]。为实现对平板式催化剂装箱效率的提升，改善工人工作状况，降低工人的劳动强度，提高企业的自动化水平和节约其生产成本，因此设计了一种能够使工人避免高强度、高密度作业的装箱自动化设备。该设备包含板材定位装置、搬运机器人装置、自动换箱装置、板材整平装置。其搬运机器人采用成本低，可靠性高，模块化程度高的直角坐标系机器人，x轴和z轴采用同步带传动方式，但考虑到带传动刚性略小[3]，属于柔性件传动，传动部分的刚度大小与伺服控制系统的闭环共振频率点息息相关，带传动很容易出现共振频率点，从而导致机器人在工作过程中的定位和速度跟踪有很大波动，且有可能出现振荡情形，显著增加机械噪音，频繁的快速启、停动作对机械结构的冲击和磨损非常严重，为了能够使平板式催化剂装箱设备在装箱过程中运动快速平稳，运动规划对平板式催化剂装箱作业显得尤为重要。

梯形速度曲线运动主要是加速度突变产生无限大的瞬间冲击量[4]，而高阶轨迹曲线，不管是加速度工作过程还是其他时刻，其冲击值始终是个非突变的数，原理上是高阶运动轨迹过程把伴随冲击释放的能量分散到加速时间段上，从而把对机器损伤程度降到最小。运动曲线阶数越高[5]，速度曲线越光滑，但是输入信号只能控制加速度和速度，加加速度是不可以控制的，只能用作计算，并且速度曲线越繁杂，就会拖慢系统的响应速度，所以在实际运用中，并不是速度曲线阶数越高设备运行效果越好。因此装箱设备中的搬运机器人和换箱装置采取的是三阶点对点运动控制模式，根据设备实物结构和工作环运动方式[6]，在传统的点对点运动规划的基础上，提出了一种以时间最优为规划目标的高精度点对点轨迹规划方法以减少对机械结构的冲击和残余振动，并用于实际工程项目中，提高板式催化剂的装箱效率。

2 装箱设备工艺动作的分析

设计的平板式催化剂装箱设备，如图1所示。其板材搬运机器人为一种三自由度的直角坐标系机器人，因为平板式催化剂装箱要求为连续的两块板要前后交错排列、水平旋转180°装箱，因此该机器人包含水平方向平移运动、竖直方向上下运动和板材抓取吸盘的旋转运动三个自由度。其运动可分为上升阶段：机器人吸盘从传送带上的抓取位置吸起产品，上升到挡板的高度；到位阶段：机器人从板材抓取位置上方移动到箱子平台位置的上方；下降阶段：机器人从箱子平台位置上方下降到箱子平台位置进行装箱，其装箱工作方向示意图，如图2所示。当箱子装满时，换箱装置开始动作，将装箱完成的换箱平台移出工位，将空箱平台移入工位，开始下一阶段的装箱过程。

图1 平板式催化剂装箱设备Fig.1 Plate Type Catalyst Packing Equipment

图2 搬运机器人工作方向示意图Fig.2 Working Direction of Handling Robot

3 高阶轨迹规划

平板式催化剂装箱设备在工作中总是常常处于快速启、停和速度较高的运动模式，其加、减速过程对机器设备的性能具有很大影响，容易激起残余振动。要使得设备运行得更稳定、快速和定位更精确，则当它启、停时需要保证速度运行曲线是平缓的[7]，而不应出现加速度突变，目前许多学者已提出了很多可行的轨迹规划及光滑处理的方法，但这些方法一般会大大增加轨迹规划的运动执行时间，影响设备运行效率，不利于向高阶扩展。因此依照高阶规划的特点，提出了一种既能满足给定速度，又能保证高阶轨迹规划运动最大参数值的一种三阶轨迹规划的控制算法，并根据轨迹的各自情况总结出其共同特征并推导其算法公式，描述了轨迹的全局预处理过程，实现了时间优化，并据此给出轨迹规划[7]的实现流程。

平板式催化剂装箱要求保证终点位置精度，点对点运动为两点间的运动，通常会采用直线运动以实现运动的快速性，并且起止点对应的约束为零，三阶点对点轨迹典型的对称位置轨迹包含匀加加速段，匀加速段，匀速段[8]，轨迹曲线，如图3所示。

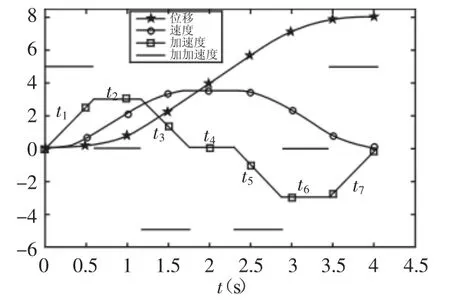
图3 典型三阶点对点轨迹轮廓Fig.3 Typical 3 Order Point to Point Trajectory Profile

但若更改某些给定的约束条件，轨迹曲线将不含匀加速段或匀速段，即运动轨迹存在多种情形[9]，通过总结分析各种情况相应的特征约束，并对相关公式进行推导，概括总结出用来判别各种情况的准则，由此实现运动轨迹的精确规划。加速度轨迹情形主要有以下几种：（1）情形一、加速度为梯形且上下两梯形不相连情形，如图4（a）所示。此情形表示整个运行位移较大，最大加速度先达最大值后，最大速度的最大值先于位移到达，此时速度轨迹含有常速段。（2）情形二、加速度为梯形且上下两梯形相连情形，如图4（b）所示。此情形表示整个运行位移较大，最大加速度先达最大值后，最大速度的最大值先于位移到达，此时速度轨迹不含常速段。（3）情形三、加速度为三角形且上下两三角形不相连情形如图4（c）所示。此情形表示整个运行位移较大、但速度小或者是运行位移小、但速度更小，在速度满足的情况下，加速度还没到达最大值，运动位移还未满足，此时速度轨迹含有常速段。（4）情形四加速度为三角形且上下两三角形相连情形，如图4（d）所示。此情形表示整个运行位移小、速度大或者是速度小位移更小，在速度和加速度都未满足的情况下，位移已到最大值，此时速度轨迹不含常速段。

图4 四种加速度轨迹情形Fig.4 Four Kinds of Acceleration Trajectories

4 三阶轨迹规划算法

三阶轨迹公式推导和算法实现：这里给定加加速度常数h，最大加速度amax，最大速度vmax，位移s。为使算法对以上四种情形都适用，故将以上四种情形都按加速度为梯形且上下两梯形不相连处理。因此，三阶轨迹运行时间被划分为7个时间段t1-t7，7个时间段对应的时间点为：

轨迹规划的加加速度为位移对时间的三阶导数，为速度对对时间的二阶导数，为加速度对时间的一阶导数，轨迹规划的数据通过积分进行计算，其计算公式，如式（1）所示。

但如果采用上述积分公式对各个时间段求解，要解大量的方程式，大大增加了计算量，因此我们在计算中不采用此方法，而采用工程中运用的面积分割法来对各时间段求解，这样就极大的简化了推导过程，体现了工程应用中直接、简单的要求。面积分割法步骤如下，根据图4，加加速度动作的时间为t1，匀加速时间段为t2，匀速时间段t4，确定了这三个参数后，再根据轨迹的对称性计算出整个轨迹的时间。在t′1时间点上加速度 a（t′1）的大小为加加速度h在时间t1段上的矩形面积，即a（t′1）=ht。在 t′3时间点上速度v3的值等于图中加速度在前3个时间段围成的梯形面积，v3=a（t′1）（t1+t2），整个位移的大小等于速度v在7个时间段上面积的总和，即s=v3（t1+t2+t3+t4）。由式（1）可以看出对三阶公式的求解就是求解加加速时间段、加速度时间段和匀速时间段，这三个参数确定后就可确定整个轨迹的运行时间。推导各时间段时间，参考基准先按极端情况考虑，即可分为两组情形，第一种是恰好达到最大加速度，并以最快的对称轨迹方式使速度和加速度为0，此时的速度和位移记为va和sa，计算公式为

第二种是速度达到最大值，并以最快的对称轨迹方式使速度和加速度为0。若加速度在速度前达到最大值，则此时的位移记为 sv1，计算公式为

若加速度在速度前未达到最大值，则此时的位移记为sv2，计算公式为

（1）当s≥sv2且vmax≥va时，此时加速度轨迹包含七段，形状为梯形不相连的情形，最大加加速时间t1由加速度确定：

由轨迹对称性可知t1=t3=t5=t7。匀加速时间段为：

由轨迹对称性可知t2=t6。匀速时间段为：

（2）当 s≥sv2且 vmax＜va时，此加速度轨迹包含五段，形状为三角形不相连的情形，最大加加速时间t1由速度确定：

由轨迹对称性可知t1=t3=t5=t7。匀加速时间段为：t2=t6=0。

（3）当s≥sa且s≤sv2时，此时加速度轨迹包含六段，形状为梯形相连情形，此时可达到的速度为：

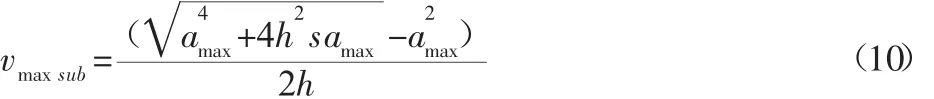
则最大加加速时间t1由加速度确定：t1=amax/h （11）

由轨迹对称性可知t1=t3=t5=t7；

匀加速时间段为：t2=（vmaxsub-a2max/h）/amax（12）

由轨迹对称性可知t2=t6；匀速时间段为：t4=0。

（4）当 sv1≤s≤sa且 vmax＜va时，此加速度轨迹包含五段，形状为三角形不相连的情形，最大加加速时间t1由速度确定：

由轨迹对称性可知t1=t3=t5=t7；

匀加速时间段为：t2=t6=0；

（5）当 s≤sa且 vmax＞va或 s≤sa且 s＜sv1时，此加速度轨迹包含四段，形状为三角形相连的情形，此时加速度最大值为：

最大加加速时间t1由速度确定：t1=amaxsub/h （16）

由轨迹对称性可知t1=t3=t5=t7；匀加速时间段为：t2=t6=0；匀速时间段为：t4=0。

经过以上过程，已求出加加速度时间段，匀加速度时间段和匀速时间段，相应的轨迹公式如下：

在t7时间段：

由于计算机在运算中会省略一部分浮点运算，会使计算精度降低，因此对此轨迹必须进行离散化处理和圆整化处理。

5 仿真及结果分析

本催化剂装箱设备的搬运机器人沿着x轴的位移需根据不同尺寸的催化剂板进行调整，其位移区间为（1.3～2）m，下面列出几组不同约束条件下的仿真结果，给定其约束参数如表1中参数一～参数四所示。

从表1可知：参数一可达到给定速度和加速度，所需总时间为4.1333s，匀加加速时间为0.3s，运动曲线有七个阶段组成，运动曲线，如图5（a）所示；参数二达到的最大速度为0.79m/s，所需总时间为3.2592s，匀加加速时间为0.3s，运动曲线有六个阶段组成，不含匀速段，运动曲线，如图5（b）所示；参数三可达到的最大加速度为0.8944m/s2，所需总时间为4.2s，匀加加速时间为0.8944s，运动曲线有五个阶段组成，不含匀加速段，运动曲线，如图5（c）所示；参数四可达到最大速度为0.7504m/s，最大加速度为0.8662m/s2，所需总时间为3.4649s，匀加加速时间为0.8662s，运动曲线有四个阶段，不含匀加速和匀速段，运动曲线，如图5（d）所示。

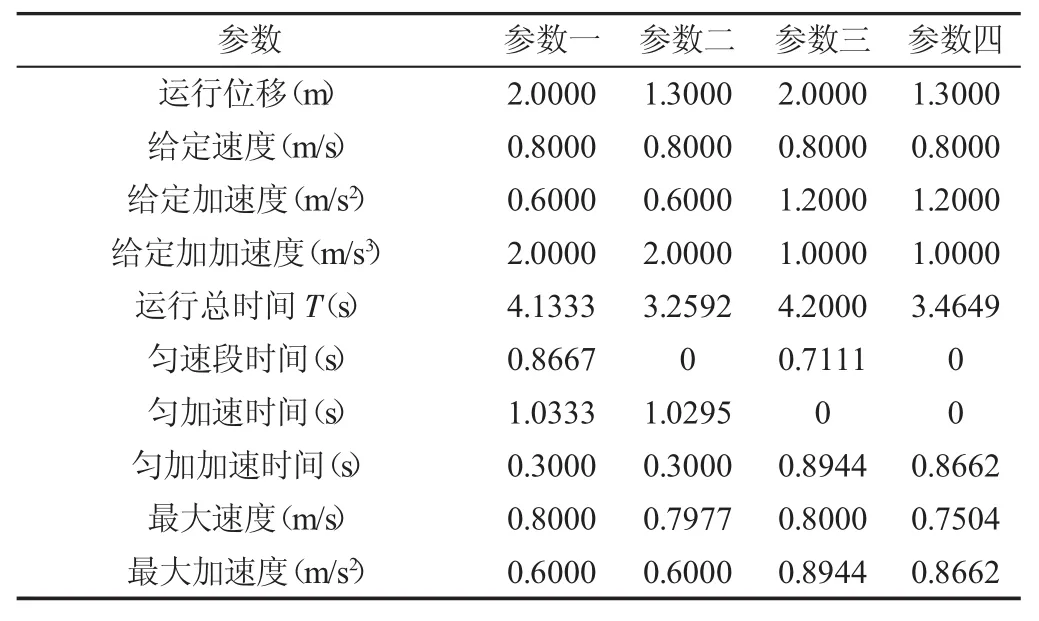
表1 给定的各组参数及其计算结果数据Tab.1 Given Parameters of Each Group and Calculation Result Data

通过对比多次仿真结果可知：（1）在给定加加速度的情况下，由于运行位移的距离不同导致加加速时间段不同，加速度和速度达到的最大值也不相等；由于给定速度或给定加速度不同得到的加速段时间也就不同，运行的总时间也有差别，给定速度越大，所需总时间越短；（2）当改变给定加加速度的情况下，给定加加速度越小，运行总时间越长。

6 结论

选用高阶轨迹对设备中搬运机器人运动轨迹进行了规划，在传统的点对点运动规划的基础上，提出了以时间顺序推导的一种以时间最优为规划目标的高精度三阶点对点轨迹规划算法，即先求出满足各个约束的时间参数，然后将各约束用时间参数表达后反向推导，最后得到轨迹规划算法，并针对设备运行位移长度的差别，进一步选出几组参数给出了仿真验证，验证了此算法可以确保加速度和速度均连续变化，该算法计算量小，较易实现编程控制，算法对控制器要求不高，可大幅节约成本，对精度有高要求的直线运动设备有很大的借鉴价值。经过试验验证，对催化剂板材搬运过程的高精度轨迹运动优化后，提高了其定位精度，并且减少了对机械结构的冲击和残余振动，运行平稳，装箱效率大幅提高，取得了预期的效果。

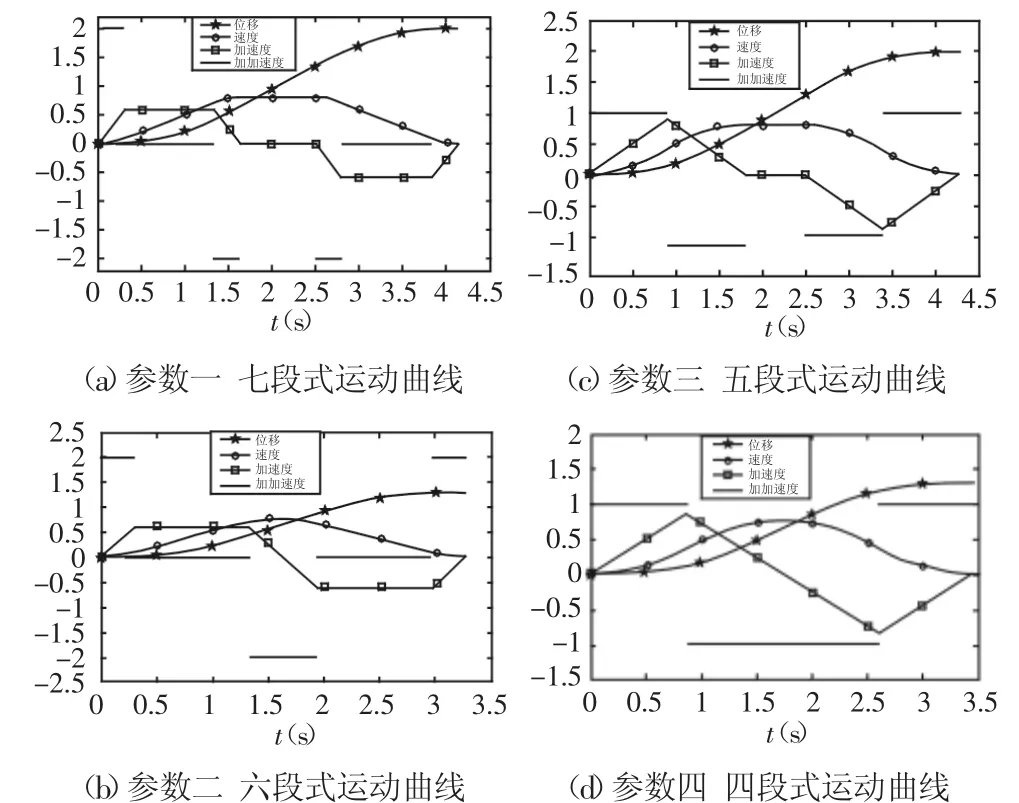
图5 几组参数对应的运动曲线图Fig.5 Several Corresponding Motion Curve of Set Parameters