桥式起重机吊重Fuzzy-LQR防摆控制器的设计

李 军，李学鋆

1 引言

起重机使用柔性绳索起吊重物使得结构轻便，提高了作业效率，但存在很大的安全隐患和控制问题。为了推进起重机吊具的自动化控制和智能化控制，对起重机吊具的防摆定位控制进行研究具有十分重要的意义[1]。针对起重机吊重防摆定位出现了PID控制、最优控制、滑模控制、模糊控制、神经网络控制、反步控制和无源控制等控制方法。由于起重机吊重的非线性特性，单一的起重机吊重防摆定位控制方式存在各种不足，因此利用多种控制方法相结合，实现优势互补，可以弥补不足，提高控制精度和控制反应速度。文献[2]建立了桥式起重机三维二自由度动力学模型、传递函数及建立仿真模型并通过解耦的处理方式利用小车控制吊重摆角，这种方式不仅可以快速控制摆角而且可以保证起重机定位。最后实验仿真验证该方法可行，但存在抖振和严重超调。文献[3]根据拉格朗日方程建立了二维门式起重机动力学模型及状态方程，利用LQR控制方法对起重机吊重摆动进行控制，仿真结果表明，给定输入的情况下，摆角可以在10s的时间保持相对稳定。文献[4]人建立了起重机吊重三维模型和动力学方程，并在x、y两方向对大小车进行解耦，并对小车进行了控制仿真。文献[5]通过找出偏差和偏差变化率与PID控制器3个参数之间的模糊关系，完成了吊重摆角的模糊PID控制设计。仿真结果证明了该方法的可行性且系统有较好的鲁棒性，系统在外界干扰的情况下30s内基本达到稳定。文献[6]建立了龙门吊车吊重二维动力学模型，运用鲁棒控制理论分析设计出了一个双闭环的PID控制系统。仿真结果表明其具有较好的稳定性能，调节速度很快，但超调量大。通过建立桥式起重机吊重三维动力学模型，并将大小车的运动状态进行解耦，通过信息融合将LQR控制的四个反馈量融合成模糊控制器的两个输入量，解决了模糊规则爆炸问题，实现了fuzzy—LQR对起桥式重机吊重摆动的控制。

2 桥式起重机三维动力学模型

桥式起重机是一个复杂的非线性系统，其系统状态不仅与自身结构和运行状态有关，还与系统所处环境有关，如所受风力影响等。为了研究方便，建立桥式起重机吊具及重物的三维简化模型[7]，如图1所示。为了使数学模型简化，对三维简化模型做以下简化：

（1）忽略摩擦力变化影响。（2）忽略绳索重量以及受力变形量。（3）忽略外界因素的影响。（4）对于一般不超过10°的小摆角，作近似处理，sinα≈α，sinβ≈β，cosα≈1，cosβ≈1，sinα·sinβ≈0，α˙2≈0，β˙2≈0，α˙β˙≈0。此外，选取 CXTD16t-19.5m 双梁桥式起重机，其参数，如表1所示。

图1 吊具工作三维示意图Fig.1 Three Dimensional Sketch Map of Hanger

表1 CXTD16t-19.5m双梁桥式起重机部分参数Tab1 Some Parameters of CXTD16t-19.5m Double Beam Bridge Crane

桥式起重机运动在某工作瞬态，假设其重物所处位置为（x1，y1，z1），小车所处位置为（x，y，0），则由图 1 得：

桥式起重机系统动能T为大小车、吊重三部分动能之和，即：

式中：x˙、y˙—大小车的位移速度；Mx、My—小车和整车质量。

根据Lagrange方程与简化条件得其动力学微分方程，如式

将方程组（3）解耦到x轴方向和y轴方向，分别得式（4）、式

其中，各参数含义及初始值，如表2所示。

表2 参数含义及初始值表Tab2 Parameter Meaning and Initial Value

由式（4）、式（5），得到大小车状态式（6）：

将表（2）参数代入式（6）、式（7）得大小车的状态空间方程：

3 LQR控制原理

LQR（linear quadratic regulator）即线性二次型调节器，其基本原理是通过寻找最优反馈矩阵K以达到最优控制，使目标函数J达到最小值，目标函数为

式中：Q、R—状态量和输入变量的加权值[8]。

根据极大值原理，最优控制为：U*=-KX

反馈矩阵K=R-1BTP，P为Riccati方程非负定对称解，Riccati方程为：PA+ATP-PBR-1BTP+Q=0

用 MATLAB 中 LQR 函数求解 LQR（A，B，Q，R），可以求出最优反馈系数矩阵K，加权矩阵Q，R矩阵。不同的K矩阵会有不同的Q、R和系统性能指标。

4 模糊控制器设计

4.1 信息融合

由大小车动力学方程设计LQR控制器的反馈矩阵有四个控制对象，以小车为例，即

反馈矩阵为：K=（KXKX˙KαKα˙）

模糊控制器的输入为偏差量E和偏差变化率Ec，显然四个输入会存在模糊规则爆炸的问题，因此必须对其降维处理，即信息融合技术。通过信息融合技术得：

此时，模糊控制器的输入由4维降到2维，满足模糊控制器的输入条件。

4.2 模糊控制策略

4.2.1 变量模糊化

经过信息融合的反馈矩阵后以偏差E和偏差变化率EC输入到模糊控制器中，即二维模糊控制器[9]。E、EC和输出变量U均定义7个模糊子集，分别为负大、负中、负小、零、正小、正中、正大，分别用NB、NM、NS、Z0、PS、PM、PB表示，每个变量论域均定为［-3，3］，其隶属度函数，如图2～图4所示。

图2 E隶属度函数Fig.2 Membership Function Figure of E

图3 EC隶属度函数Fig.3 Membership Function Figure of EC

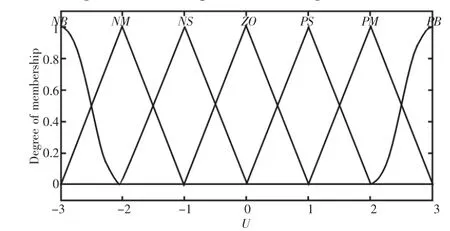
图4 U隶属度函数Fig.4 Membership Function of U

4.2.2 模糊推理规则

根据输入变量和输出变量论域的划分，设计出Mamdani型的模糊推理规则，采用重心法解模糊，由于每个变量均有7个语言值，因此设计出49条规则，控制规则，如表3所示。

表3 模糊控制规则Tab.3 Fuzzy Control Rule

利用MATLAB的Fuzzy工具箱建立隶属函数和推理规则。

4.2.3 量化因子

E、EC的量化因子KE、KEC将E、EC分别从基本论域转换到各自的模糊集论域，控制量U的比例因子KU也需要将U从模糊集论域转换到基本论域中[10]。量化因子除了对论域进行变换外还使前后模块匹配，对整个系统有调节作用，因此三者的大小通过仿真确定。

5 仿真

5.1 仿真模型

结合建立的动力学方程在simulink中搭建大小车仿真模型及联合仿真模型，如图5、图6所示。

图5 小车控制仿真模型Fig.5 Control Simulation Model of the Crane Crolley

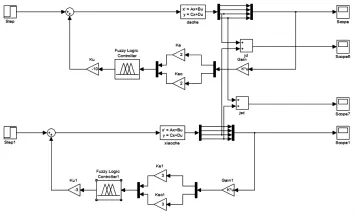
图6 联合控制仿真模型Fig.6 Joint Control Simulation Model

仿真过程中给定仿真初始值为（0，0，0.2，0），即给定的初始角度为0.3rad，输入单位阶跃信号，如图5所示。大车仿真过程中给定仿真初始值为（0，0，0，0），即给定的初始角度为 0rad，输入单位阶跃信号；仿真过程中给定的仿真初始值为（0，0，0.5，0），即给定初始角度为0.5rad，输入单位阶跃信号，如图6所示。

5.2 仿真参数的确定

由于系统的位移和角度对系统稳定性影响最大，因此，取大车的加权矩阵 Q大=（300，1，200，1），R 大=1。利用 MATLAB 的LQR 函数求解得出反馈矩阵 K大=（17.32，21.68，-1.89，8.1108），计算出信息融合矩阵K*大：

小车的加权矩阵 Q=（450，10，300，10），R大=1。利用 MATLAB的 LQR 函数求解得出反馈矩阵 K小=（21.21，11.73，5.730，16.52），计算出信息融合矩阵：

KE、KEC、KU分别取 2、2、-10，仿真初始值取（0，0，0.2，0）。

5.3 仿真结果

吊重在未加入控制前的仿真结果，如图7所示。由图7可知未加入控制时吊重摆动初始角度为0.2rad，运动过程中摆角变化曲线和角速度变化曲线均做小幅度衰弱波动。

分别对大小车进行仿真，仿真结果，如图8、图9所示。由图8 可知，给定初始值（0，0，0.2，0），在外界输入的情况下，吊重各运动参数可以迅速达到平衡，摆角稳定较快，历时14s但存在超调，且在小车位移值达到0.9m时，小车速度、吊重摆角、吊重角加速度达到稳定。由图9可知，在无初始值的情况下，当大车输入阶跃信号时，大车速度、吊重摆角、吊重角加速度在位移量为0.42m的时候达到稳定状态，但四个运动参数的调整时间长，存在超调和抖振现象。由图10可知，对大小车的联合仿真时，给定初始状态（0，0，0.5，0），经过 30s的调整，基本可以达到稳定状态，15s吊重摆角可以达到0.02rad范围内，但存在超调。

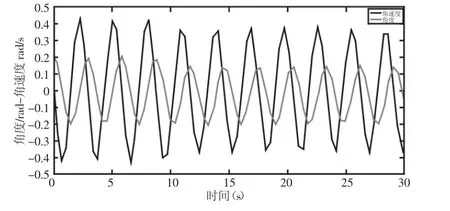
图7 未加入控制时吊重参数变化曲线Fig.7 Parameter Changing Curve of Crane Load Without Adding Control

图8 小车仿真结果Fig.8 Simulation Result of the Crane Rrolley Rontrol

图9 大车控制仿真结果Fig.9 Simulation Result of the Crane Cart Control

图10 联合仿真角度变化曲线Fig.10 The Curve Change of Angular of Joint Control Simulation

图11 联合仿真角速度变化曲线Fig.11 The Curve of Angular Velocity Change of Joint Control Simulation

6 结论

将吊重运动解耦到大小车的运动方向，分别利用大小车的运动控制吊重摆动以及利用二者联合控制吊重摆动。对比加入控制前后的吊重摆动仿真结果表明，Fuzzy-LQR控制方法可以完成对桥式起重机吊重的防摆定位，动态响应速度快，调整时间较短，且通过调整控制参数Q、R、KE、KEC、KU可以改变控制结果，调节超调量和动态响应速度。