Stewart并联机器人控制算法研究

文 刚，高宏力，彭志文，梁 超

1 引言

Stewart六自由度并联平台结构非常的典型，其具有的特点包括：自由度多、刚度高、精度高、承载能力强以及可模块化生产等等，所以应用的领域非常广泛。其主要应用地方有操作器、运动模拟器、并联机床、坐标测量机、医疗以及航空航天等多个方面，并要求平台的运动系统具有很高的控制精度以及较快的动态响应性能，因此平台的控制算法是六自由度并联平台研究的一个热门问题，也是一个难点问题。

六自由度平台的控制方式有很多，例如PID及其增强型控制、自适应控制、变结构控制以及鲁棒控制等[1]，但是由于其耦合性强、非线性度高、动力学模型复杂等原因，使得一些自适应的控制方法计算量大，对于快速且实时的需求难以满足，而且在应用鲁棒控制时，其鲁棒性和控制的精度要求难以同时满足，因此不适用于此类复杂系统[2]。在并联平台的控制中，必须要用到基于模型的控制算法。计算力矩就是根据平台的动力学方程而设计的一种PD控制器，通过计算每个缸体的施加力的大小，然后通过运动学分析，可以实现对平台的精确控制。为了解决系统的不确定性以及控制过程中的各种干扰，使用了模糊算法实时修正计算力矩中的控制参数。

2 动力学模型

Stewart并联机构的结构图，如图1所示。平台的运动系统采用的是电机驱动的方式进行的。机器人的六个支腿由六个电动缸构成，电动缸由电机直接驱动，作为平台的作动器协调动作，六个支腿综合产生上平台的运动。上下平台与作动器的连接方式依靠的是虎克铰，由此每个支腿有着两个转动副和一个移动副。连接上平台的虎克铰由于与对应的转动副是异面共点的，所以可将此虎克铰视为球铰来分析。文章介绍的控制算法是基于动力学模型的，采用的动力学方程模型引用自参考文献[1]。首先把整个平台分为两大部分：分别为上平台和六个电动缸组成的可伸缩作动器。因为下平台固定不动的，视为与地固连，所以此时可以忽略不用考虑。然后建立静坐标系为绝对坐标系和与上平台固连的体坐标系为相对坐标系，选择上平台与支腿的连接位置qp作为广义坐标，选择其速度q˙p为广义速度，并且应用拉格朗日法求得上面铰点处的约束力。最后把上平台作为研究对象，应用Newton-Euler法得到整个并联机器人的完整的动力学方程。

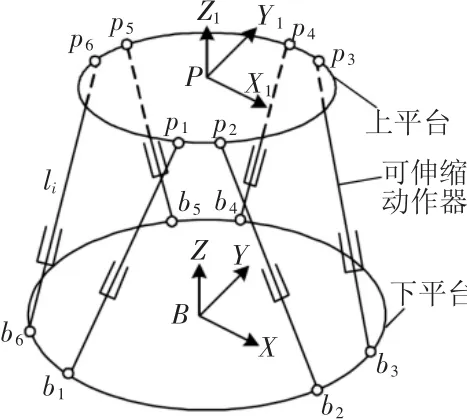
图1 Stewart平台结构示意图Fig.1 The Schematic Diagram of the Stewart Platform

机构的动力学方程式如下式所示：

由于我们设计的计算力矩控制算法是基于铰点的控制算法，所以还需要对式（1）进行修改，改为建立其定义于铰点空间的Stewart机器人动力学方程，修改后的公式如下式：

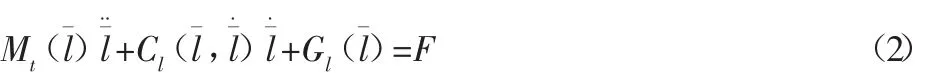
式中：M（q）—平台的正定的惯性矩阵；C（q，q˙）q˙—平台的向心和科氏力矩向量；而C（q，q˙）—平台向心和科氏力矩的系数矩阵；G（q）—平台重力矩阵—从上平台广义速度到电动缸伸缩速度的雅可比矩阵；—从上平台广义速度到上铰点速度的雅可比矩阵；mp—上平台及上平台上其他物体总的质量；mt、mb—电动缸支腿上下部分的质量；g—重力加速度；It、Ib—机构支腿上、下部移动部分相对于静坐标系的惯性张量的分量。

3 控制器设计

因为Stewart平台为典型的非线性、耦合性强的时变系统，应用传统的控制算法难以实现对平台的准确控制，很难到达满意的控制结果，所以为了构建一个精度高、效果好的控制系统，采用模糊计算力矩的控制方法。应用模糊算法优化计算力矩控制参数的示意原理图，如图2所示。其主要的核心为计算力矩控制算法，再应用模糊算法对计算力矩控制器的参数进行实时的在线的优化，实现平台的更加灵活的控制。

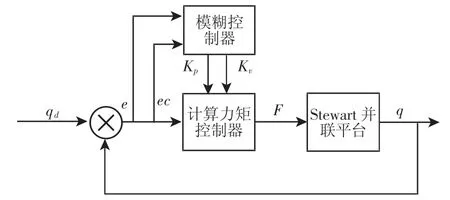
图2 模糊计算力矩控制系统结构图Fig.2 Structure of Fuzzy Computed Torque Control System

3.1 计算力矩

计算力矩控制算法在机器人的控制方法中非常的常规，等同于基于动力学模型的PD控制算法，主要是利用平台的动力学模型和平台控制的路径规划结合运动学来计算出各缸体的瞬时施加力，Stewart机构的动力学方程，如式（2）所示。

所以将式（2）代入式（3）可以得到：

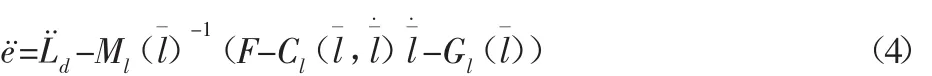
定义其控制输入函数为：

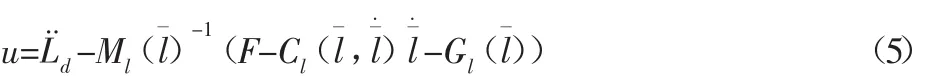
则可以将式（5）变形为：

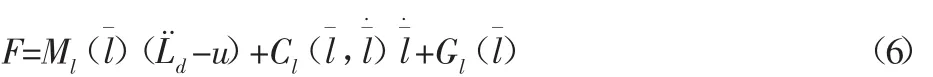
式（6）即为力控制律。

反馈环采取PD控制，反馈控制律为：

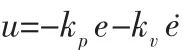
式中：kp—比例系数；kv—微分系数。

则平台的控制输入为：

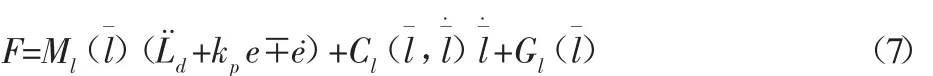
计算力矩控制算法是PD控制，所以对计算力矩参数的整定即为整定kp、kv的值。从整个系统的稳定性、响应快慢、控制准确度等方面来综合考量：kp的作用是为了提升系统的响应速度和控制准确度；kv是改善系统的动态性能。同时在整定kp、kv的值的时候还得考虑两个参数之间的耦合关系。

针对不同的e和Δe，Δkp、Δkυ的整定原则有如下几点：

（1）当e较大时，为了使系统更快速的调节同时跟踪性能更好，kp应该取得较大，kv的值应该取得较小。

（2）当e、Δe 中等时，为了避免过大超调，可以将kp的值减小一下。在这个时候，系统对于kv的反应较为敏感，所以对kv的值要取得相对小一些。

（3）当e较小时，为了保证系统的稳定性，kp应该取得较大。同时，当 Δe 较大时，kv的值应该取得较小；当 Δe较小时，kv的值应该取得较大些。

3.2 模糊计算力矩

针对Stewart并联平台的特点，根据计算力矩控制参数的整定方法，可以设计一个2输入2输出的模糊控制器。2个输入分别为电动缸的位移量的预期值和实际值的差值e及其变化率ec，2个输出分别为Δkp、Δkv，以实现对计算力矩算法的在线整定。kp、kv的在线整定公式为：

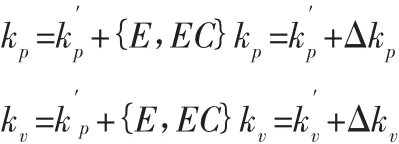
根据计算力矩Δkp、Δkv的整定原则，创建了模糊计算力矩的模糊规则表，如表1所示。

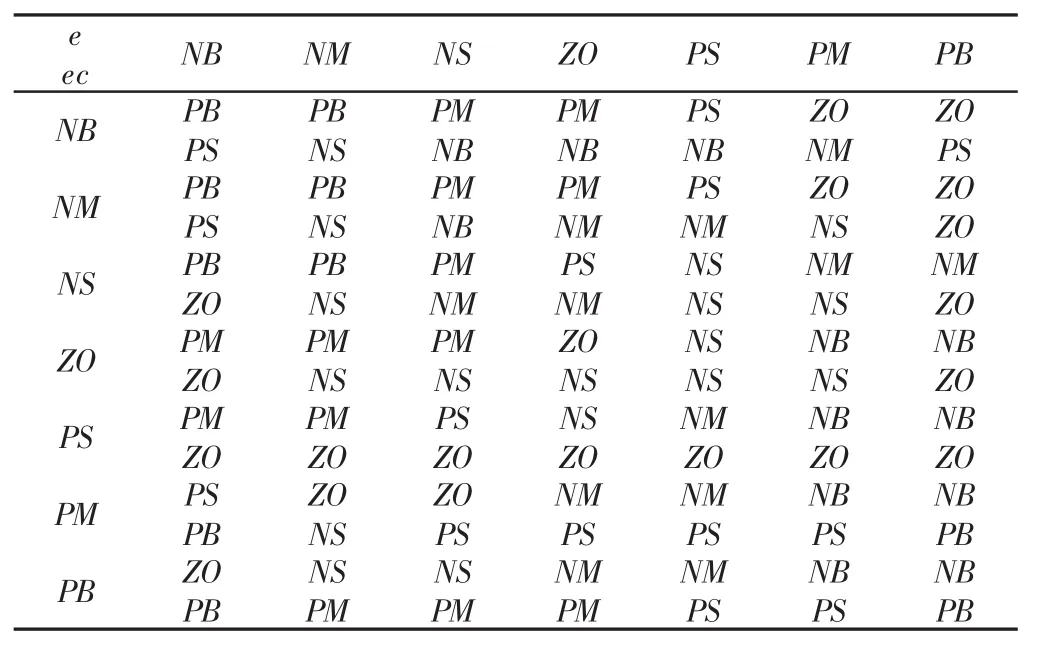
表1 Δkp、Δkv的模糊控制规则表Tab.1 Fuzzy Control Rule Table of Δkp、Δkv

表 1中 NB、NM、NS、ZO、PS、PM、PB 是采用的 7个模糊子集来表示模糊控制器的输入输出变量，其含义分别为：正大、正中、正小、零、负小、负中和负大。

4 仿真实验

在这一部分，使用了MATLAB/Simulink对控制Stewart并联平台的各种算法进行了仿真，使用的算法有PID控制、计算力矩以及文章所提的模糊计算力矩，目的是为了对应用的这三种控制算法进行对照分析，找到模糊计算力矩控制算法相对于其他两种算法所对应的优势。文章应用MATLAB的SimMechanics工具箱建立了平台的仿真模型，然后将建立的平台仿真模型放入Simulink中与其他控制部分组成一个完整的仿真系统。SimMechanics是专门为机构和控制器建模的一种工具箱，所有的操作都是基于Simulink环境进行的。平台的主要基本参数，如表2所示。

表2 Stewart平台参数Tab.2 Parameters of the Stewart Platform

平台末端的运动轨迹方程如下所示：

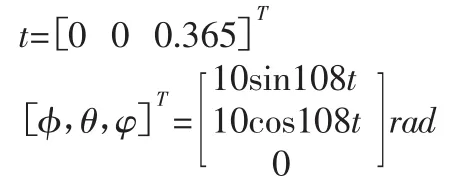
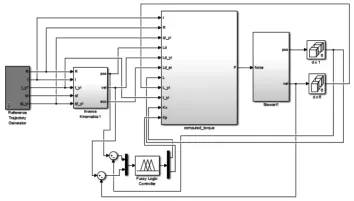
图3 Simulink仿真模型Fig.3 Simulation Model in Simulink

这里的结果分析主要是将末端平台的轨迹运动应用并联平台的运动学转换为六自由度并联平台的六个支腿的运动，然后再对六个支腿的运动精度进行分析对比。系统仿真模型，如图3所示。应用PID控制算法、计算力矩以及模糊计算力矩控制算法时，六个支腿的误差，如图4～图6所示。

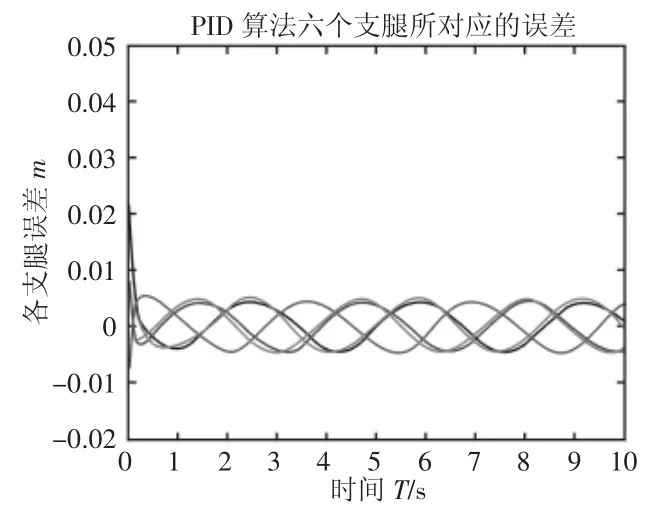
图4 PID算法六个支腿所对应的误差Fig.4 Six Cylinder Errors of PID

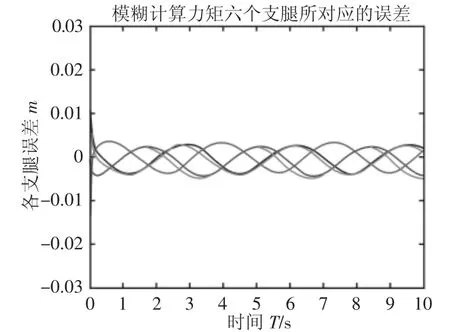
图5 计算力矩六个支腿所对应的误差Fig.5 Six Cylinder Errors of Computed Torque Method

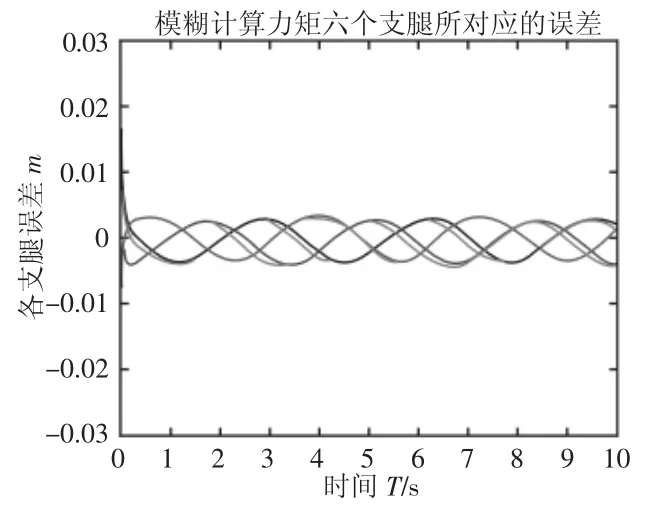
图6 模糊计算力矩六个支腿所对应的误差Fig.6 Six Cylinder Errors of Fuzzy Computed Torque Method

通过图4可以看出，在控制系统在应用传统的PID算法时，六个支腿的误差最后稳定时在0.004m以内，通过计算得出其误差最大为5.7%。再通过图5，再应用计算力矩的控制算法时，可以明显的看出六个支腿在初始位置时的误差就有了很大的改善，并且能够更快的趋于稳定，稳定后精度也较高，最后稳定时误差在0.0029m以内，其计算出其最大误差为4.1%。平台应用模糊计算力矩控制器时六支腿的误差，如图6所示。可以看出应用该算法时，平台的控制更加的精准，收敛的速度也更快，稳定时误差不超过0.0025m，最终计算出的误差最大不超过3.6%，且此时整个系统也更加的趋于平稳。

5 结论

根据Stewart并联机器人动力学模型的特点而设计的模糊计算力矩控制器，与PID的常规传统的控制方法和基于动力学的计算力矩控制方法进行对照和分析，这种方法不仅保证了较快的收敛速度和更高的控制精度，而且能够通过模糊控制器实时的改变计算力矩控制器的控制参数，使得控制过程更加的灵活和准确。同时，该方法结构比较简单，效率也较高，可以适用于Stewart并联机构或其他类型的并联平台。