修井机刹把布置仿真及优化研究

屈文涛，赵摇摇，徐剑波

1 引言

修井机作为石油机械的重要设备，具备了起升幅度高、工作效率高等优点[1]。在油气田修井过程中，司钻工承受大负荷、高频率、长时间的工作。司钻工工作过程中，拉刹把动作最为频繁，若刹把布置不合理，会导致司钻工施力不当，长久以此，会加剧司钻工患职业病的概率。

随着HSEMS在国内外各油田的大力施行，用户对石油装备人性化设计的要求愈加苛刻[2]。受到车辆保有量、行业观念等因素的限制，关于石油特种车辆的人机工程学研究与应用远远落后于行业普遍水平[3]。关于修井机刹把的布置优化研究相对较少，束奇等人依据人机工程学设计理论与修井机作业要求，对大刹、操纵杆等主要元件进行了人机优化设计，并利用CATIA软件的RULA法对修井机司钻工作业姿态进行评估[4]。RULA姿势评价法的数据是基于观察法的基础上，而不是基于实验数据，且对某些姿势无法进行更为细化的评价[5]。

以XJ30修井机为例，借鉴AMS软件在飞行员推拉操纵杆动作仿真等成功案例[6-8]，以修井机操作舱内刹把铰接位置为对象，将肌肉激活度作为疲劳评价指标，结合人机工程学理论与AMS软件，对司钻工拉刹把动作进行逆向动力学仿真，应用最小二乘法理论建立最大肌肉激活度拟合方程，为修井机操作舱内拉刹把动作引起的人体疲劳定量评价提供依据。

2 仿真模型

2.1 刹车系统工作原理

刹车系统为手动带式刹车，手动刹车机构工作原理，如图1所示。当需要刹车时，司钻工捏紧手把，通过拉伸弹簧伸缩，带动闸刀离开齿板，此时拉刹把，刹把绕铰接轴转动，带动调节叉杆运动，进而拉动刹带拉肘，使刹车带抱住刹车鼓，在摩擦力的作用下达到制动目的。司钻工频繁拉刹把过程中，会引起肌肉的疲劳，合理地布置修井机刹把铰接位置可减少司钻工的工作强度，减轻疲劳。

2.2 人机交互仿真模型建立

以XJ30修井机操作舱为例，通过测量得到操作舱环境中座椅、刹把等尺寸，在Creo软件中建立操作舱的三维模型，将三维模型转化为STL格式添加到AMS软件中。为了尽可能满足更大百分比的人群，选用P5、P50、P95百分位人体模型；石油修井机司钻工常为男性人群，所以根据GB10000-1988推荐的男性人体尺寸，在AMS软件中分别建立了中国成年男子人体模型，如图2所示。

图2 P5、P50、P95百分位中国成年男子人体模型Fig.2 Body Model of Chinese Male Adult of the 5th，50th，95th Percentiles

修井机司钻工进行刹车动作时，捏紧手把是小施力动作，对本研究结果影响较小，所以对于拉刹把过程，忽略司钻工手捏手把动作。通过设置人体模型的初始姿态，调整人体模型的位置角度，以铰接方式实现刹把与铰接轴的连接，刹把绕铰接轴转动来改变刹把的角度；通过支撑点方式将司钻工与座椅、人体足部与地面进行连接；通过铰接方式将手与刹把进行连接，分别建立了各百分位司钻工与操作舱的交互模型，如图3所示。交互模型全局坐标的原点位于人体坐姿时两坐骨结节连线与脊柱的交点处，刹把铰接的横、纵向位置分别用x和y坐标轴表示。

图3 司钻工与操作舱的交互简化模型Fig.3 Human-Computer Interaction Model of Driller and Control Cabin

2.3 肌肉模型的选取

在AMS软件中，针对多刚体骨肌动力学问题采用逆向动力学方法解决，逆向动力学是根据物体的运动现象，利用力学定律来求解使物体运动发生变化的动力学表达[9]。在人体逆向动力学分析中，人体可用的肌肉数量多于所需要驱动的关节数量，会使骨肌系统产生肌肉冗余问题。为了解决肌肉冗余问题，AMS软件中采用下列形式实现最优化目的[10-11]：

式中：G（f（M））—目标函数；d—已知的外力与惯性力，N；f→—肌肉力与关节力，N；C—常系数矩阵—第i块肌肉的肌肉力，由于肌肉力只能拉不能压，所以肌肉力具有非负性，N。

关于目标函数最小化的问题，AMS软件中最常用的是最大最小疲劳准则与多项式准则，其形式分别如下：

式中：Ni—第 i块肌肉的生理横截面积（PCSA），N/Ni—第 i块肌肉的肌肉激活度；n（M）—已知的肌肉总数；多项式准则中P=3。

式中：σi—肌肉极限张力。

虽然最大最小准则相对于多项式准则可以更加快速、稳定的获得优化结果，但是它的计算不是连续可微的，而多项式准则不存在此缺陷，因此选取多项式准则为肌肉优化方法。

3 逆向动力学仿真分析

3.1 参数设置

根据P95百分位人体模型中右手可达区域，选取坐标x变化范围为（-0.025～0.6）m，坐标 y变化范围为（0.5～0.875）m，将铰接位置区域划分为（26×22）的坐标空间。通过运动捕捉仪器测得刹把拉至极限位置的制动时间为1s。人机工程学中要求前后向杠杆的手控操纵允许用力不超过150N，设手臂承受的最大拉力为100N，XJ30修井机刹把高度为0.8m，可得人体所受最大阻力矩为80Nm。刹把拉至极限位置的角度为30°，由人体所受最大阻力矩与刹把极限位置角度，可得刹把的弹簧刚度为153Nm/rad。设人体与地面及座椅摩擦系数分别为0.2、0.5。

3.2 仿真结果分析

多项式准则是关于肌肉激活度的函数，肌肉激活度是一个归一化参数，其数值越大，表明肌肉负荷越大，人体越疲劳。当肌肉激活度达到或者超过100%时，肌肉处于过劳状态，最大肌肉激活度是肌肉激活度的最大值，可作为判别肌肉是否处于疲劳状态的直接指标[12-13]。以最大肌肉激活度作为疲劳评价指标。

提取AMS软件仿真所得各百分位人体模型的最大肌肉激活度与刹把铰接位置的横、纵坐标数据，剔除人体不能触及刹把的点及刹把与人体产生干涉的点，将仿真数据导入到Matlab软件中，分别获得对应百分位人体模型的最大肌肉激活度与刹把铰接位置的散点图，如图4所示。

由图4知，虽然随着人体百分位数的增加，人体可触及域增大，但对于不同百分位人群，其变化趋势基本一致。当纵坐标不变时，随着横坐标的逐渐增大，人体最大肌肉激活度逐渐增加，人体最大肌肉激活度在横坐标的右边界处取得最大值，最大值为0.99。横坐标的变化趋势远大于纵坐标的变化趋势，表明横坐标比纵坐标对人体最大肌肉激活度有更大影响。

图4 不同百分位最大肌肉激活度散点图Fig.4 Max-Muscle Activity of the 5th,50th,95th Percentiles

4 最大肌肉激活度数据拟合

4.1 最小二乘法拟合方程建立

将AMS软件仿真所得数据导入到Matlab软件中，运用最小二乘法理论拟合出各百分位人体最大肌肉激活度与刹把铰接位置的响应曲面，如图5所示。

根据图5的响应曲面变化趋势，分别假设人体最大肌肉激活度与刹把铰接位置是一次、二次、三次函数关系，函数表达式分别为：

式中：x—刹把铰接的横坐标，m；y—刹把铰接的纵坐标，m；z1、z2、z3—一次、二次、三次函数的人体最大肌肉激活度；a1、a2、a3、b1、b2、b3、c1、c2、c3、d2、d3、e2、e3、f2、f3、g3、h3、i3、k3—常系数。

将仿真数据代入式（7）、式（8）及式（9）中，运用最小二乘法理论获得式（7）～式（9）的方程表达式系数，建立对应百分位人体最大肌肉激活度与刹把铰接位置的各阶次拟合方程。表1为P50百分位最大肌肉激活度的一次、二次、三次函数表达式系数。

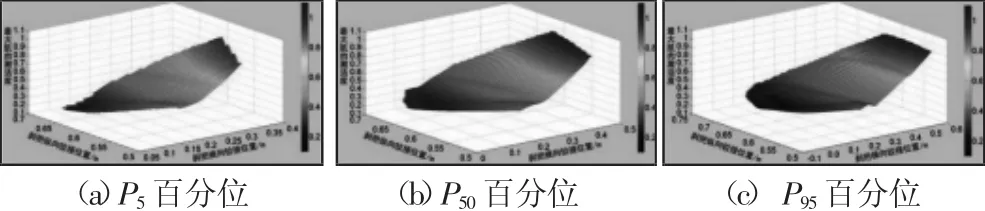
图5 各百分位最大肌肉激活度响应曲面Fig.5 Response Surface of Max-Muscle Activity of the 5th，50th，95th Percentiles

表2 最大相对误差及相对误差置信区间Tab.2 Maximum Relative Error and Confidence Interval of Relative Error

图6 P50百分位最大肌肉激活度方程拟合曲面Fig.6 Fitting Surface of Max-muscle Activity of the 5th Percentile

图7 P50百分位最大肌肉激活度相对误差Fig.7 Relative Error of Max-Muscle Activity of the 5th Percentile

4.2 拟合结果误差分析

置信水平是指总体参数值落在样本统计值某一区域的概率，置信区间是指在某一置信水平下，样本统计值与总体参数值间的误差范围，常以95%置信水平为指标。

以相对误差最大值及置信水平为95%的相对误差置信区间为指标，根据所求的拟合方程分别拟合出人体最大肌肉激活度与刹把铰接位置的一次、二次、三次拟合曲面，求解响应曲面与各阶次拟合曲面的相对误差。分别比较各百分位人群相对误差的最大值及置信水平为95%的相对误差置信区间，优选出拟合曲面的表达式。P50百分位最大肌肉激活度的拟合曲面，如图6所示。P50百分位最大肌肉激活度的响应曲面与各阶次拟合曲面的相对误差，如图7所示。各百分位人群拟合曲面相对误差及置信水平为95%的置信区间，如表2所示。

由图6可知，对于P50百分位人群，随着拟合方程阶次的增加，拟合曲面与响应曲面的变化趋势具有更好的一致性。由图7可知，对于P50百分位人群，拟合方程的相对误差随着阶次的增加而减小，最大肌肉激活度拟合曲面与响应曲面的拟合效果更好。

由表2可知，对于各百分位人群，随着拟合方程次数的增加，相对误差的最大值减小，各百分位人群的三次拟合方程的最大相对误差不超过11.2082%；在置信下限相同，拟合曲面的置信水平为95%时，相对误差的置信上限逐渐减小，当拟合曲面为三次方程时，置信上限值最小，不大于0.0755，即对于三次拟合方程，95%的相对误差不大于7.55%。

对于各百分位人群，人体最大肌肉激活度与刹把铰接位置的函数表达式选择三次方程为最佳，各百分位拟合方程表达式为：

式中：z5、z50、z95—第 5、50、95 百分位人群最大肌肉激活度；x—刹把铰接的横坐标，m；y—刹把铰接的纵坐标，m。

5 结论

（1）应用AMS软件建立了修井机操作舱的人机交互模型，对P5、P50、P95百分位人群拉刹把动作进行逆向动力学仿真。结果表明，各百分位人群人体最大肌肉激活度与刹把铰接位置的变化趋势基本一致，刹把铰接的横向位置比纵向位置对人体最大肌肉激活度的影响更大。

（2）运用最小二乘法理论建立了最大肌肉激活度与刹把铰接位置的拟合方程，并对拟合方程进行了相对误差分析，得到三次拟合方程相对误差最小，且拟合曲面与响应曲面更接近，所以三次拟合方程为最优。

（3）人体最大肌肉激活度与刹把铰接位置拟合方程的建立缩短了产品设计周期，降低了设计成本，为修井机操作舱内刹把布置优化研究提供了依据。