液压支架反冲洗滤芯可靠性试验及研究

朱天涛，刘混举

1 引言

据统计，液压系统80%以上的故障是由液压污染引起的，而过滤器滤芯在污染控制中起着及其关键的作用，只要滤芯失效，很容易引起液压元件腐蚀、磨损、管路堵塞等各种问题，从而造成系统不能正常工作[1]，因此，进行滤芯可靠性的研究十分必要。对于矿用支架反冲洗滤芯，目前从未有专门的设备去检测其质量，也从未评定过其可靠性，对其进行合适的可靠性试验，构建恰当的可靠性数学模型，从而有效评定滤芯可靠性水平，指导其设计和制造，具有重要的理论和实践意义。

由于反冲洗滤芯失效难以判别，首次开发矿用滤芯结构完整性试验台，以特定条件下滤芯的首次冒泡压力为标准判断其是否失效[2]，再结合煤炭企业实际生产和设备维护，进行定时间隔测试的截尾可靠性试验[3]。在试验数据分析和建模过程中，考虑工程上常用的威布尔分布[4]，同时提出不同失效模式对建模过程的影响，改进了其方法，最终成功构建了滤芯可靠性数学模型，有效评定了其可靠性水平，同时找出了设计制造缺陷，利于其改进生产。

2 可靠性试验

可靠性试验常指产品在贮存、工作条件下或模拟加速条件下进行的寿命试验[5]。对于精度很高，修复难度大的滤芯来说，第一次失效显现的规律特性代表了其寿命特征。因为反冲洗滤芯的失效不通过专门设备检测难以发现，因此实时监测失效情况的传统可靠性试验难以进行，结合企业设备维护时间，设定间隔时间为1个月的定时截尾试验。进行试验是同种型号未使用过的50个反冲洗滤芯，为便于以后试验数据以间隔时间分组，由统计学经验公式[6]：

带入n=50，得出k=7，即设定试验时间为7个月。

2.1 反冲洗滤芯失效判定

滤芯的失效具有隐蔽性，很难通过肉眼或简单方法鉴别，对于一般的滤芯，除了结构上的损坏，纳污容量与其寿命关联很大，当容纳污染物达到一定程度，压降会达到滤芯规定压降，也代表着滤芯失效[7]，但对于反冲洗滤芯，由于具有反向冲洗污染物的功能，纳污容量不能作为其寿命判断的根据，结构性失效成为主要原因，在这种情况下，通过滤芯的结构完整性试验可以有效判定滤芯是否失效。因为国内制造厂方并不能提供滤芯的规定冒泡压力，此次可靠性试验所用滤芯参照国外标准，按照其精度，材料及结构，规定冒泡压力为1200Pa，根据工程经验和滤芯性能试验，当冒泡压力低于规定的80%时，会明显影响滤芯性能，即当滤芯结构完整性试验首次出现连续气泡的压力值低于960Pa时，就判定滤芯失效。

2.1.1 结构完整性试验原理

专门用于矿用反冲洗滤芯的结构完整性试验台并不存在，但可以借鉴用于燃油过滤滤芯的实验台进行改进和开发，使得实验台符合反冲洗滤芯的大小，材料等条件，其试验原理，如图1所示。气源处是由空压机提供的压缩空气，管路中设置了各种气动元件，以调节流量，压力，并保持气体的清洁，被测滤芯浸没在特定的试验液体中，控制装置可以控制滤芯的升降便于装卸，同时也可以使滤芯绕轴线旋转以观测冒泡点的准确位置。当气体以较小的压力注入滤芯时，由于试验液体的张力作用，气体不会从液面逸出，即没有冒泡；逐渐调节压力，当达到一定压力时，气体压力大过液体的张力，就会出现冒泡现象。由于液体的张力与孔径的大小成反比，所以首次出现稳定气泡的位置就是滤芯的最大孔径位置，如果冒泡压力与规定压力相差较大，就说明滤芯的结构受到损坏。

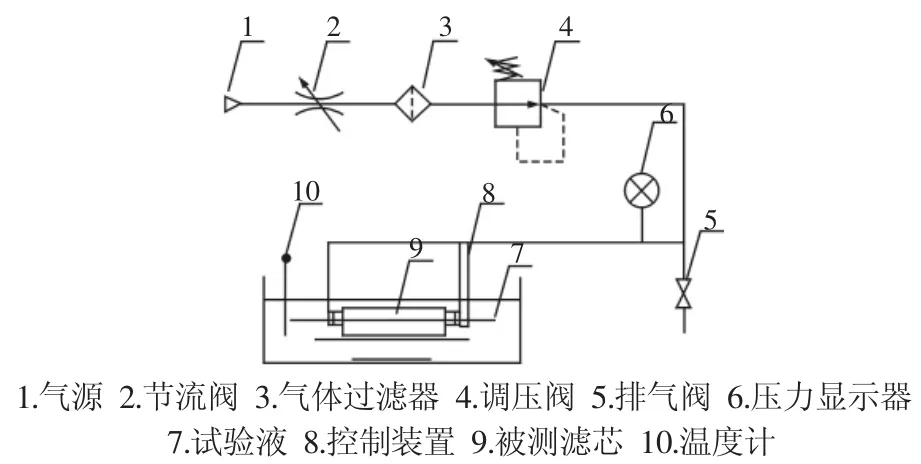
图1 结构完整性试验原理图Fig.1 Schematic Diagram of Structural Integrity Test

2.1.2 结构完整性试验步骤

（1）放置滤芯，浸泡足够时间后调整液面至规定高度。

（2）控制滤芯绕主轴缓慢旋转，同时通入气体，缓慢调整压力，压力每增加100Pa，滤芯至少旋转360°。

（3）逐渐增加压力，直到首次出现连续稳定冒泡现象，记录此时压力值，冒泡位置及试验液温度。

（4）释放气压，再重复试验两次，共记录三次数据。

2.2 可靠性试验记录

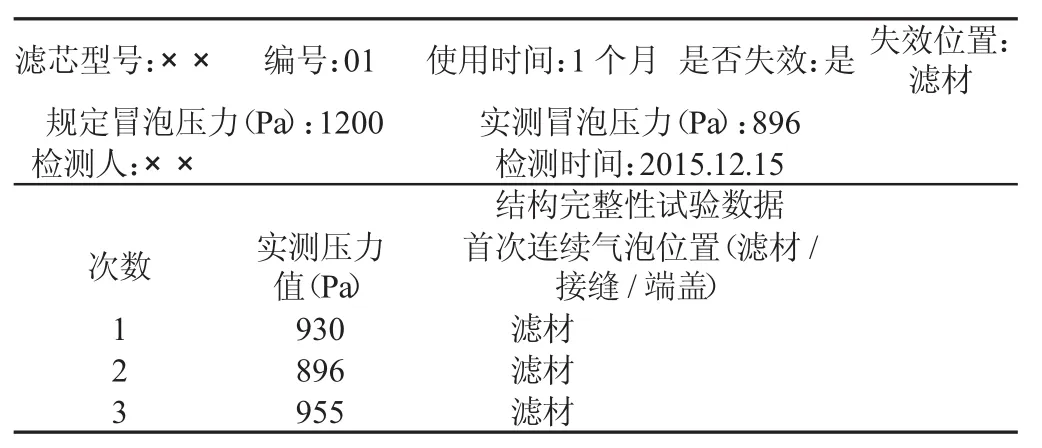
表1 可靠性试验记录表Tab.1 Record List of Reliability Test

以试验的50个新滤芯正式投入生产之日算起，每隔一个月进行全部的结构完整性检测以判断其是否失效，若有失效的滤芯，则不再使用和检测，一共检测7次，在每次进行检测时，填写可靠性试验记录表，如表1所示。在与规定冒泡压力进行对比时，要使用三次试验的最小值，通过记录和整理，结合滤芯的失效判定试验和实际生产过程，得到可靠性试验的数据。

3 可靠性数学模型构建

在机械可靠性工程数学模型的构建时，常常运用威布尔分布，因为此分布可以很好地显示出机械疲劳，磨损，腐蚀等失效形式的规律，但事实上，威布尔分布的前提是假定机械零件的各种失效方式都有着相同的失效函数，这对于失效模式状况不同的机械产品来说，存在着较大的误差。对于反冲洗滤芯，它的结构性失效主要表现在滤材、接缝和端盖，这里面每种失效模式的失效机理并不是明显相同的。因此，考虑对每种模式所造成的失效进行分别的统计和模型构建，最后根据失效模式间的相关性确定整体的可靠性模型，将接缝失效的模式称为模式一，滤材为模式二，端盖为模式三，这样分别对统计的数据进行分析和整理。

3.1 数据的初步整理

对定时截尾的可靠性试验的数据画出记录图，如图2所示。因为这次试验是运用间隔时间观测的方法进行的，所以无法准确标定每个样本失效的具体时间，因此以试验时间为横坐标，失效个数为纵坐标，对传统的截尾试验示意图进行合适的改变。

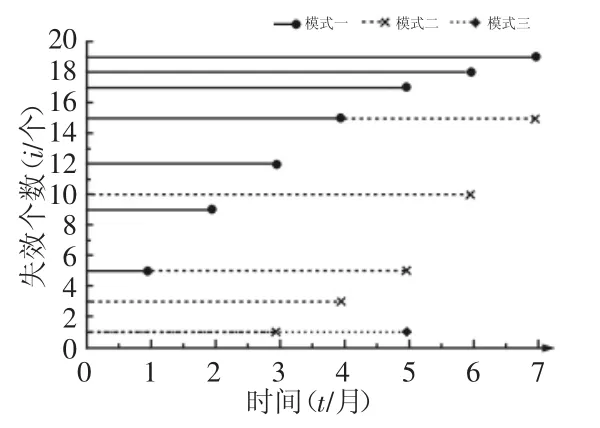
图2 可靠性试验记录图Fig.2 Record Chart of Reliability Test

通过记录图可以清楚地得到每种失效模式在每个时间段引起滤芯失效的个数，在其中取符合条件的随机点，可以近似得到每种失效模式导致滤芯失效的累计失效概率分布，当然，也可以得到其近似的失效概率密度函数图，如图3所示。因为端盖失效只在第5个月时才发生一次，以后也没有再发生过，因此判断为偶然失效，不进行分析和建模。

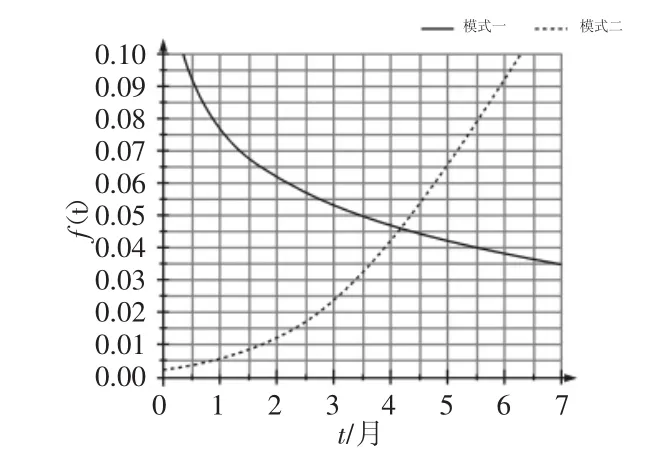
图3 失效概率密度函数图Fig.3 Failure Probability Density Function

3.2 失效分布函数的确定

虽然在考虑到失效模式差别比较大时，放弃了对滤芯整体运用威布尔分布建立模型，但对于每个失效模式本身，可以作为一个单元假定其服从威布尔分布进行建模，这符合威布尔分布的推理过程，因此，设两种失效模式其概率密度函数都服从两参数威布尔分布，其公式为[8]：

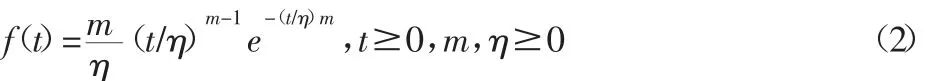
式中：m—威布尔分布的形状参数；η—尺度参数；t—时间，月。

由于进行的是定时间隔测试的截尾试验，因此，如果试验样本数为 n，在时间 t1，t2，t3，…，tk进行观测，至 tk时停止试验，具体失效时间落入时间间隔（ti-1，ti）的样本个数为ri（i=1，2，…，k），那么ri个滤芯在时间间隔（ti-1，ti）内失效的概率为：

n-r个滤芯到tk时间未失效的概率为：

那么似然函数：

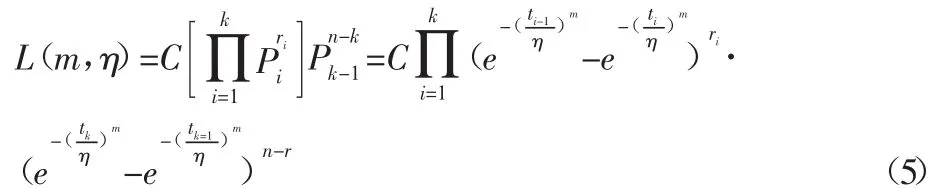
式中：C—常数。

对上式取对数并求导得到似然方程：

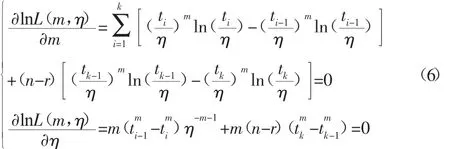
由于此次可靠性试验用的是等时间间隔的观测，因此t1=h，t2=2h，…，tk=t7=7h，其中h为间隔时间，即h=1，单位是月。由可靠性试验记录图可知，对于模式一影响的失效来说，r1=5，r2=4，…，对于模式二影响的失效来说r1=0，r2=0，r3=1，…r7=5。

运用数值分析的方法解出似然方程，带入h和r后分别得到模式一和模式二威布尔分布失效概率密度函数的m，η极大似然估计值。求得：

对于并没有明显的相关性的失效模式，而且其中任意一种失效都会导致滤材的失效时，其总分布的累计失效分布函数为：

带入数值，可以得出，模式一，模式二以及滤芯总累计失效分布函数为：

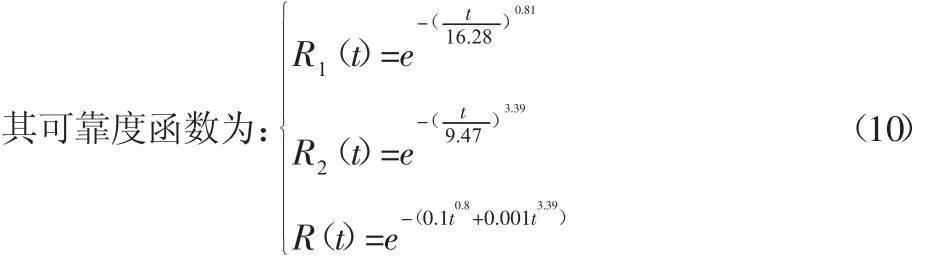
3.3 失效分布函数的拟合检验

在进行拟合检验的时候，因为没有确切的数值，只能在规定的范围内任取几个随机数，进行近似的拟合，假定检测时恰好发生本间隔时间内最后一个失效，这样可以确定七个确切的坐标，在origin软件中，分别对模式一累积失效分布函数，模式二累计失效分布函数，滤芯总的累计失效分布函数进行拟合检验，如图4所示。

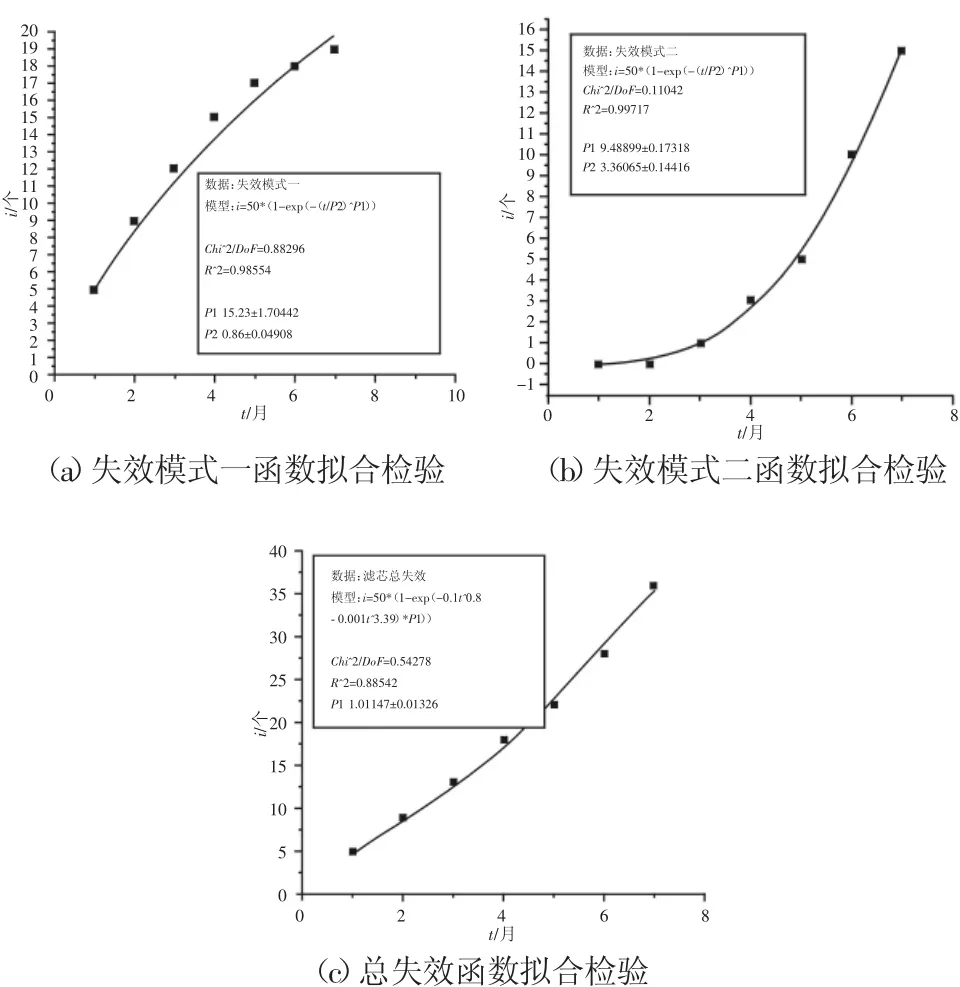
图4 拟合检验图Fig.4 Fitting Test Chart

拟合检验用的是origin中非线性拟合的功能，对两个失效模式的函数，设定参数P1，P2分别为η和m，对于总失效函数设定比例系数P1，将求取的值分别作为初始值带入，进行卡方检验和多次拟合运算，最后得到卡方检验接受函数的假设，多次拟合得出的最佳值与计算值差距在5%以内，拟合度很高，这表明所求分布失效函数是可以接受的。

4 可靠性分析和讨论

由可靠性试验数据得出其数学模型，并经过拟合检验确定其可以接受，进而在企业中进行同种型号反冲洗滤芯的抽样检测，表明其失效情况大致符合模型，这说明进行的建模是可靠的，因此，根据数学模型对此种反冲洗滤芯进行可靠性的分析和讨论。根据滤芯总失效累计分布函数可以得到，当其使用半年时，可靠度为0.5，到厂家标称的使用寿命三年时，其可靠度已几乎为0，这表明此种滤芯的可靠性水平很差，需要慎重选用。由滤材失效分布函数可知，其m值为3.36，处于3和4之间，根据威布尔分布的性质可以知道，此时分布近似于正态分布，正态分布一般用于显现由累计的各微小随机因素共同导致的失效，如机械产品的磨损，腐蚀等，这表示制造及偶然因素对滤材的失效影响不大。此滤芯在短时间内滤材失效率很低，但过了初始期后，失效情况迅速增多，说明其所用材料和乳化液介质和井下环境相容性不是很好，只有在前期才能比较好地经受住环境的应力，可以推断其所用不锈钢和滤纸等有一定的质量缺陷。对于接缝失效，其m值为0.8，小于1，说明其失效率是逐渐降低的，这表示接缝在使用前期失效率很高，很明显有着重大的制造缺陷，其胶接或焊接工艺需要进行改进。

5 结论

（1）开发的矿用反冲洗滤芯结构完整性试验台运行良好，其检测结果经过多通试验以及实际使用情况验证，能够准确判断滤芯的失效情况，可以作为反冲洗滤芯失效检测设备。（2）由滤芯总的失效可靠度分布函数可以确定，所选的这种型号滤芯可靠性水平很差，远远达不到其规定的要求，但此滤芯在煤矿企业的使用非常广泛，这种情况应该得到重视，最好形成煤矿企业倒逼制造商进行产品升级和可靠性建设的机制。（3）滤芯结构性失效两大原因，接缝失效和滤材失效，其失效分布函数分别近似服从m值小于1的Weibull分布和正态分布，表明分别是制造工艺和材料不良引起的失效，其中接缝处的焊接工艺不合格是滤芯失效的主要原因，应该重点加以改进。此次关于矿用反冲洗滤芯可靠性的试验与研究对以后滤芯的可靠性试验，可靠性建模，可靠性评价，可靠性提升等有一定数据和方法上的借鉴意义。