微型抗磁悬浮振动能量采集器静平衡研究

苏宇锋，秦立振

1 引言

Earnshaw定理[1]指出，永磁体不能在外界静磁场中实现稳定的悬浮，除非有外力使其保持平衡。随着抗磁性材料的发现，抗磁悬浮系统的可行性[2]得到了论证，并且在1939年，Braunbek在不均匀的强电磁场（2.1～2.4）T中利用微小片状石墨和铋建立起来悬浮[3]。此后，抗磁悬浮的研究一直在不断的发展。

利用抗磁悬浮能够在常温下获得稳定无摩擦悬浮这一特点，很多学者将抗磁悬浮系统应用到不同的研究领域中。文献[4]将一个包含小型悬浮永磁体的抗磁悬浮系统应用在磁驱动薄膜执行机构中，通过悬浮永磁体的稳定悬浮来调节磁驱动薄膜的中间位置，在感应线圈内通入交流信号，则会改变悬浮永磁体所处环境的磁场，进而驱动执行机构运动。文献[5]则利用磁偶极子模型和图形法对垂直方向上的抗磁悬浮系统进行了理论分析，利用半解析法和离散体积法对系统中提升永磁体、悬浮永磁体和圆柱型热解石墨材料薄板进行参数化研究，以分析这些参数对悬浮永磁体悬浮间隙、系统的尺寸以及固有频率的影响，在此基础上设计出的振动式能量采集器，在加速度为0.081m/s2，频率为2.1Hz的外界激励下，产生的有效输出功率为1.72μW。文献[6]将通电导线圈包覆在环形永磁铁外，并且不同的位置包覆的线圈匝数不同，这样就得到了外形上近似为圆锥，倒圆锥和菱形的等效提升永磁体，通过改变通电导线圈内的电流来改变悬浮永磁体所受外界磁场的磁场强度，进而得到悬浮永磁体在垂直方向上稳定悬浮空间的变化，并通过理论分析，发现要获得更大的稳定空间就需要距离提升永磁体更远，或者能够使得在悬浮永磁体处的磁感应强度关于位置变化的二阶导数更小。文献[7]则分析了非垂直方向上实现稳定悬浮的条件，通过理论分析，模拟仿真以及实验验证，实现了在水平方向上的稳定悬浮。文献[8]则利用这一方案实现了在低频外界振动作用下的能量采集器的设计，所设计的能量采集器的共振频率为1.2Hz，输出功率为3.6μW。

文献[9]利用在垂直方向上比较容易实现抗磁悬浮设计出了一种能量采集器，但只分析了在两热解石墨板间距一定时的悬浮状态，并未就两热解石墨板间距变化对悬浮永磁体悬浮状态的影响予以深入讨论。在文献[9]提出的抗磁悬浮能量采集器结构基础上，通过有限元软件仿真计算，分析了悬浮永磁体平衡位置和两热解石墨板间距的关系，并通过实验予以验证。

2 装置模型与理论分析

抗磁悬浮系统中永磁体的磁场强度以及抗磁性材料的磁化率是影响悬浮系统的两个关键的参数。永磁体的磁场强度越大，抗磁性材料的磁化率越大，两者之间相互作用的抗磁力也越大。因此，选择磁能积和矫顽力比较大的钕铁硼（NdFeB）作为悬浮系统中永磁体材料，选择磁化率很大的热解石墨（磁化率χ=-450×10-6）作为抗磁性材料。抗磁悬浮能量采集器自上而下是由提升永磁体、上热解石墨板、悬浮永磁体、下热解石墨板以及镀在两热解石墨板上线圈组成，其模型侧重受力分析，没有画出线圈，如图1所示。其中，悬浮永磁体受力分析，如图2所示。

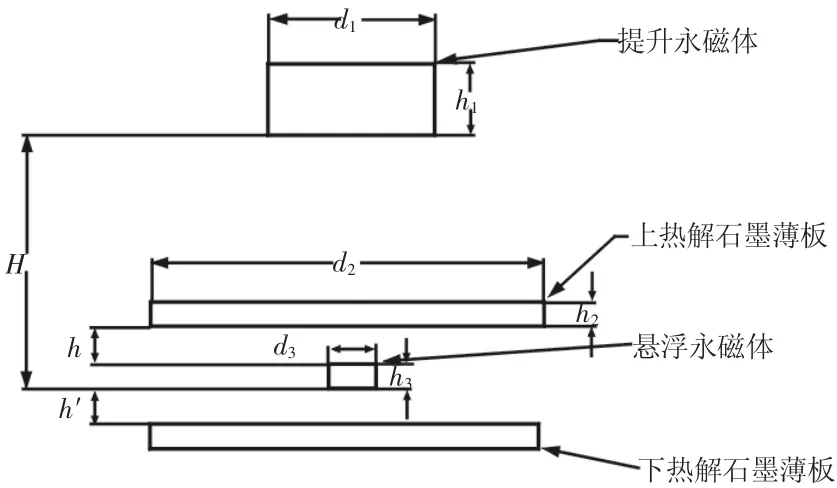
图1 抗磁悬浮能量采集器结构模型Fig.1 The Structure Model of Energy Harvester Based on Diamagnetic Levitation

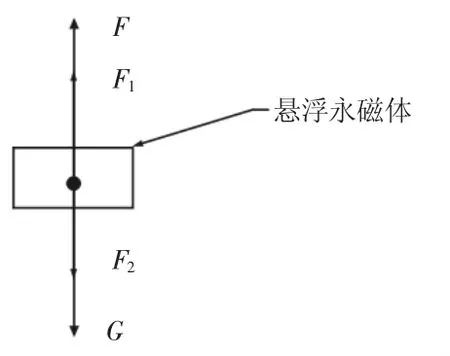
图2 悬浮永磁体受力分析图Fig.2 The Force Analysis of Floating Magnet

在竖直方向上，悬浮永磁体受到提升永磁体对其作用的吸引力F，上下热解石墨板对其作用的抗磁力F2、F1以及其所受到的重力G，因此，悬浮永磁体所受合力：

在稳定状态下，悬浮永磁体所受合力F合=0，悬浮永磁体在实验中稳定时的悬浮状态，如图3所示。

图3 实验装置图Fig.3 The Experimental Setup for This Study

当外界对悬浮装置施加振动激励时，由于热解石墨板上的铜线圈和悬浮永磁体振动不同步而发生相对运动，进而切割磁感线，在线圈内产生感应电动势。

为求得悬浮永磁体所受合力和系统各参数之间的关系，需要将悬浮永磁体所受各个力进行参数化表示。提升永磁体对悬浮永磁体在竖直方向上的作用力可用如下表达式计算。

式中：d1、h1、d3、h3—提升永磁体和悬浮永磁体的直径和厚度；μ0=4π×10-7H/m，为真空中磁导率；M1、M2—提升永磁体和悬浮永磁体磁化强度。

下热解石墨板对悬浮永磁体在竖直方向上的作用力可从文献[10]推导如下：

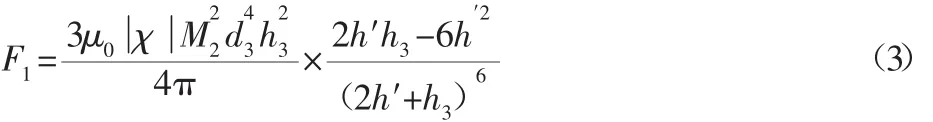
相似地，上热解石墨板悬浮永磁体作用力为：

从图1中模型的几何关系可知，两热解石墨板间距L为：

不难看出，当h=h′时，两热解石墨板对悬浮永磁体作用力大小相等，方向相反，如果此时提升永磁体对悬浮永磁体作用的引力和悬浮永磁体所受重力相等，即F=G，那么F合=0。可求得：

式中：ρ=7.4×103kh/m3，为永磁体材料钕铁硼（NdFeB）的密度。

以H0作为运动初始位置，向下为正方向，位移x，其作用力随位置变化关系式为：

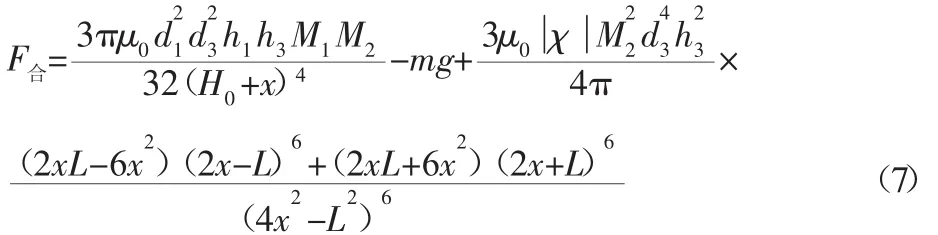
从式（7）可以看出，两热解石墨板间距L对悬浮永磁体在偏离初始位置x时所受合力有很大影响。为便于计算，利用有限元软件COMSOLMultiphysicsTM建立装置模型，进行受力计算，并通过MATLAB进行多项式拟合，进而求得平衡位置与两热解石墨板间距的关系表达式。

3 抗磁悬浮装置模型仿真分析

在有限元软件COMSOLMultiphysicsTM下建立抗磁悬浮装置模型，模型参数，如表1所示。对该模型进行静力分析，通过消除磁力计算的累积误差[11]后进行数据处理，得到提升永磁体与悬浮永磁体之间作用力随其间距H变化曲线，如图4所示。悬浮永磁体受到的单块热解石墨板对其的抗磁力随两者之间间距h变化曲线，如图5所示。

表 1抗磁悬浮装置有限元模型建模参数Tab.1 Parameter for the Finite Element Model of the Diamagnetic Levitation Structure

图4 磁力随间距H变化曲线Fig.4 Curve of Magnetic Force Varying with Gap H

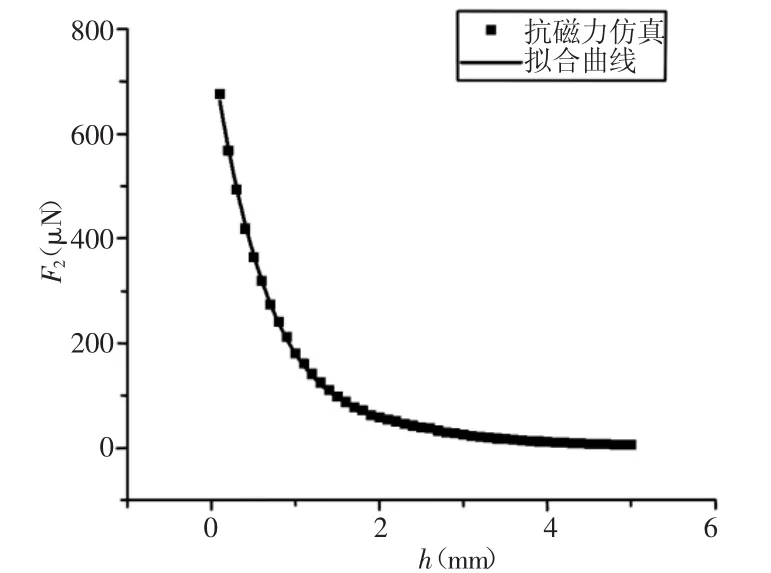
图5 抗磁力随间距h变化曲线Fig.5 Curve of Diamagnetic Force Varying with Gap h

通过对图4和图5中仿真得到的力分别进行多项式拟合可得：

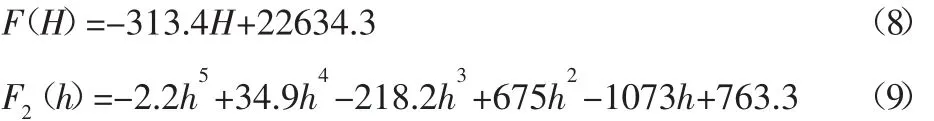
这样得到悬浮永磁体的受力与两热解石墨板间距L和位移x的关系表达式为：

为便于分析，令：

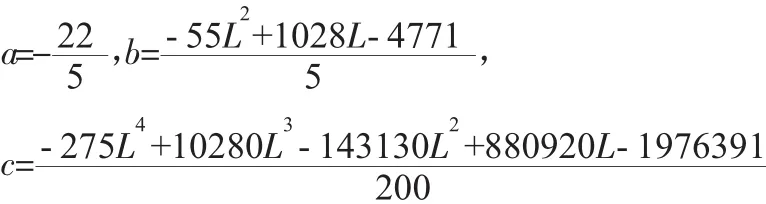
显然，x=0是方程F合=0的一个根。方程是否还有其它实根，则需要分析：

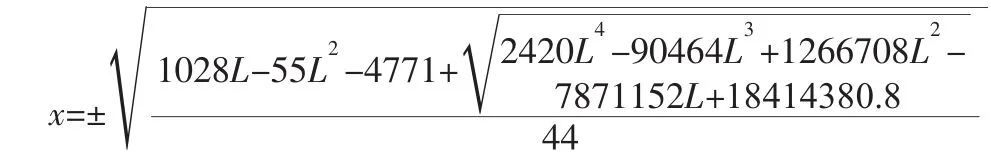
4 悬浮永磁体静平衡位置分析与实验验证

由以上分析可知，在两热解石墨板间距L在L＞5.54mm时，悬浮永磁体所受合力有3个零点，但这3个零点并非全是平衡位置。选择两热解石墨板中间对称平面为势能为0的平面，绘制悬浮永磁体在两热解石墨板间距为5mm和7.4mm时，和对称平面相距x的受力和势能曲线，如图6所示。由势能变化曲线可以看出，当热解石墨板间距L=5mm时，势能在悬浮永磁体活动空间内只有一个最低点，由能量最小原理可知这个点即是悬浮永磁体的平衡位置。而当L=7.4mm时，在x=0处，即两热解石墨板对称平面上，悬浮永磁体势能并不是最低，悬浮永磁体并不能够稳定静止，它会向能量更低的方向运动。因此x=0点并非其运动的平衡位置，通过之前分析得到受力的另外两个零点才能够保证悬浮永磁体稳定悬浮。

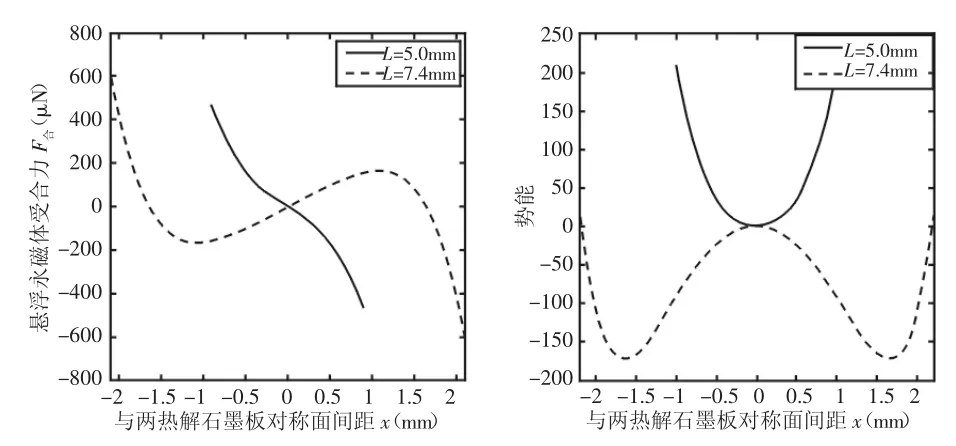
图6 热解石墨板间距分别为5mm、7.4mm时悬浮永磁体受力和势能变化Fig.6 The Resultant Force and Potential Energy of Floating Magnet Varying with Distance x when the Gap of Two Pyrolytic Graphite Plates are 5mm and 7.4mm

为了验证上述关于悬浮永磁体静平衡位置的研究结论，我们搭建了如图3所示的实验装置对抗磁悬浮装置中悬浮永磁体的平衡位置加以研究。两热解石墨板间距分别为7.4mm和5mm时悬浮永磁体悬浮状态，如图7所示。通过实验发现在两热解石墨板间距为5mm时，悬浮永磁体能够稳定悬浮在两热解石墨板中间对称面上，给悬浮永磁体一微小扰动，经过一段时间后，其仍能回到初始位置，因此，在板间距为5mm时，悬浮永磁体呈现出单平衡现象。当两热解石墨板间距为7.4mm时，悬浮永磁体并不能够在两热解石墨板对称面处悬浮，它会朝着其中一个热解石墨板运动，然后逐渐稳定悬浮下来，给予悬浮永磁体以扰动，悬浮永磁体会越过两热解石墨板对称平面在接近另一个热解石墨板处稳定悬浮下来，也即悬浮永磁体出现了明显的双平衡位置现象。图8则给出了理论曲线和通过实验观测到的数据点，可以看出，在双平衡位置处，通过仿真计算得到的关系曲线和实验数据的变化趋势是相同的，只是在数据的契合程度上比较大的偏差，这是因为：（1）实验中所用的永磁体会和其所标定的规格有偏差。（2）实验中热解石墨板厚度并不均匀（2.8～3.1）mm。（3）实验环境达不到仿真环境的理想程度。

图7 热解石墨板间距分别为7.4mm和5mm时悬浮永磁体悬浮状态Fig.7 The States of Suspension of Floating Magnet when the Gap of Two Pyrolytic Graphite Plates are 7.4mm and 5mm

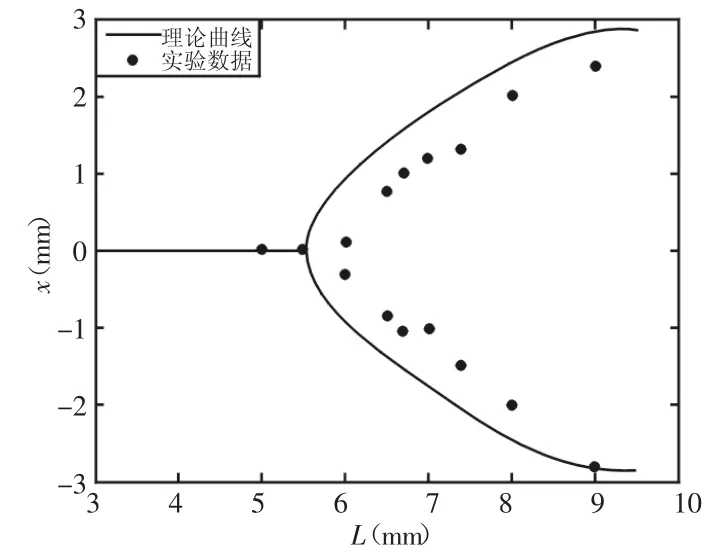
图8 平衡位置x随两热解石墨板间距L变化Fig.8 The Equilibrium Position x Varying with the Gap L of Two Pyrolytic Graphite Plates

5 结论

通过对抗磁悬浮装置中悬浮永磁体受力的理论分析和仿真计算，发现当两个热解石墨板间距变化时，悬浮永磁体在两热解石墨板间的平衡位置会发生变化，并且会出现多个平衡位置的现象。对抗磁悬浮能量采集器，当两块热解石墨板间距L处在时，悬浮永磁体只有一个平衡位置，平衡位置位于两热解石墨板中间对称面上。当两块热解石墨板间距处在时，悬浮永磁体有两个平衡位置，这两个平衡位置相距两热解石墨板对称面的间距呈对称分布。搭建实验平台，通过实验验证了悬浮永磁体平衡位置的存在。在实验中发现会实验结果和理论曲线变化趋势相同，但数据点会有误差，分析了这种误差产生的原因，进一步验证了理论分析的合理性。

抗磁悬浮振动能量采集器的平衡位置的确定是能量采集器的设计和应用上很重要的前提，但由于能量采集器的工作过程中其悬浮是动态的，因此研究工作过程的平衡位置的影响因素对分析能量采集器的稳定性、安全性以及输出特性上都有很大的价值。研究为抗磁悬浮能量采集器工作过程的平衡位置的研究提供了理论基础和实验依据。