动态轧制力下冷连轧机超亚谐共振特性分析

彭荣荣，巩长芬，王国威，秦梅宝

1 引言

冷连轧机的振动问题一直颇受国内外学者的关注，加之随着当代生产技术水平的不断提高，钢铁行业对轧制速度、产品质量和精度等的要求也随之提高，而冷连轧机辊系的振动会造成带材质量、精度等下降，严重时可导致带材断裂、设备损坏、次品积累，给企业造成困扰和经济损失[1-3]。

海内外学者对冷连轧机的振动形式和机理从各种角度、不同影响因素进行了分析探究，建立了多种振动模型，对抑制轧机振动取得了很好成果。文献[4-5]建立了受前后张力和轧制速度影响的轧机垂直振动模型，分析了带钢动态运动的稳定性，提出了相应的抑制措施；文献[6]探讨了摩擦因数对轧机垂直振动的影响，得出了轧制乳化液的润滑性能与摩擦因数之间的非线性关系；文献[7-9]对四辊板带冷轧机在辊缝变形较大情况下的振型做了详细分析，发现在某些特定频率下轧机工作辊和支承辊在垂直方向上的振动幅度较大，且在这个过程中摩擦力的影响极大；近年来，研究人员对影响轧制力的种种因素进行了深入分析，通过考虑轧辊及轧件的弹塑性变形、带钢厚度、张力、辊缝接触弧长、轧制速度、润滑等不同因素影响下的轧制力模型，在此基础上，文献[10-13]提出了动态轧制力这一概念，其更加符合轧机实际振动过程中的动态变化。在动态轧制力的基础之上，考虑了冷连轧机的机械结构、辊系间的阻尼及非线性刚度、周期性外激力等因素，建立了基于动态轧制力的冷链轧机振动模型，得到了相应的动力学方程，研究了在不同参数变化下的冷连轧机3次超谐共振和1/3亚谐共振幅频特性，仿真分析给出了这两种具有不同振动特性下轧机稳定运行和发生失稳时的参数区域，可以避免参数的选取不合理而导致的轧机剧烈振动。

2 轧机振动系统动力学建模

四辊冷连轧机的简化模型，如图1所示。将上支承辊等效称成一个集中质量块[13]，且考虑轧机到上、下辊系以及沿轧件运动方向的上、下两部分振动具有高度对称性[10]，建立了基于动态轧制力下的冷连轧机非线性振动动力学模型，如图2所示。

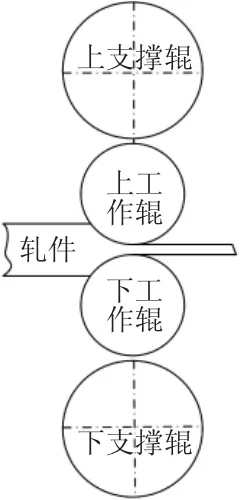
图1 四辊冷连轧机简化模型Fig.1 The Simplified Model of Four-High Cold Rolling Mill

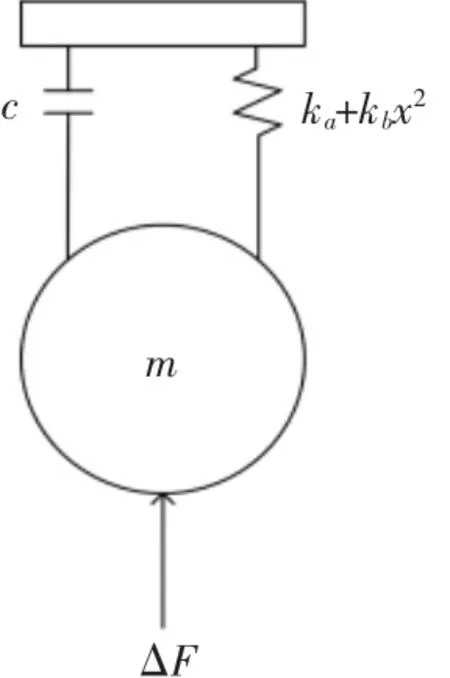
图2 冷连轧机非线性振动动力学模型 Fig.2 The Nonlinear Vibration Dynamic Model of Cold Rolling Mill

图中：m—冷连轧机工作辊的等效质量；c—其结构阻尼，用Duffing振子ka+kbx2表示支承辊与工作辊之间的非线性刚度[14-15]，ka，kb—静态及动态刚度；ΔF—轧制力的动态变化部分，是关于振动位移 x的非线性函数[10]，ΔF=b1x+b2x3。b1，b2—待定常数。由图2的力学模型可得冷连轧机动力学振动方程为：

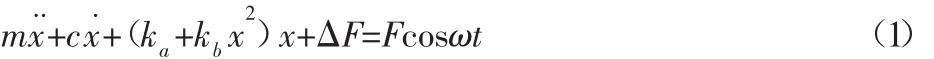
式中：F cosωt—冷连轧机受到的周期性外激力，且令式（1）中：

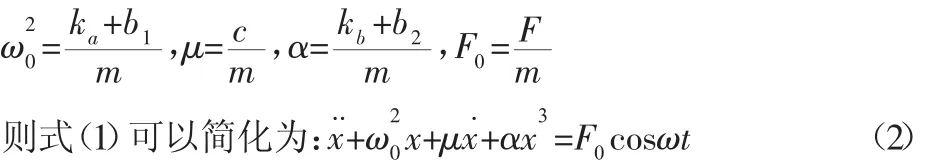
式（2）为考虑轧机结构，辊系间的非线性刚度，动态轧制力以及周期性外激力影响的冷连轧机动力学方程，是研究分析轧机振动特性的基础。

3 轧机振动系统响应求解

式（2）中的冷连轧机动力学方程属于弱非线性系统，对其中非线性项同时冠以小参数ε，则式（2）可进一步写为：

对式（3）运用多尺度法求解，此时引入不同尺度的时间变量，即：

对时间t的微分可利用复合函数微分公式按ε的幂次展开：

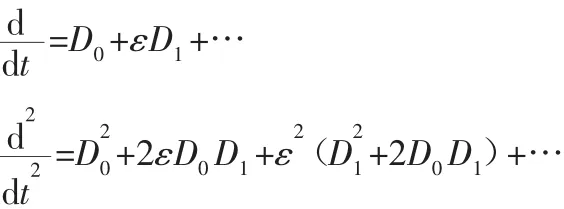
式中：Dn—偏微分算子符号，此时，关于式（3）的解可以表示为：

将式（5）代入式（3），且比较方程两边小参数ε的同次幂系数，整理可得：

设零次近似方程（6）的解为：

式中：A—复数形式的振动振幅；Λ—振动振幅的实数形式，且有：

将零次近似解代入式（7），整理后可得：

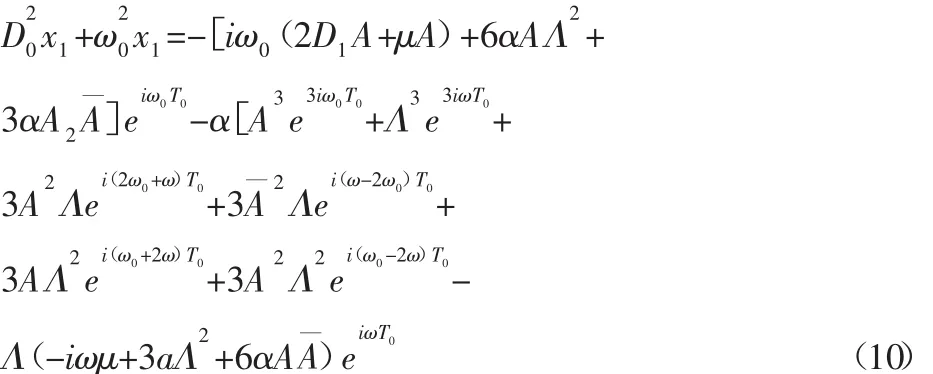
从上式各项中可以看到，含有的eiω0T0项可引起久期项，产生主共振，而e3iω0T0和ei（ω-2ω0）T0项在满足3ω=ω0或ω=3ω0时也能产生久期项，从而产生超谐和亚谐共振。下面主要讨论在动态轧制力下冷连轧机振动系统发生3次超谐共振和1/3次亚谐共振的情形。

3.1 超谐共振幅频特性方程

设ω0与3ω的差别为ε的同阶小量，即3ω=ω0+εσ，σ为调谐参数，为了消除式（10）中的久期项，必须使：

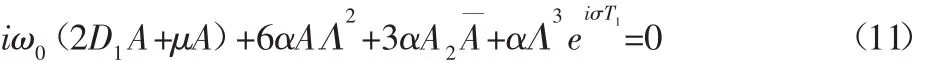
令 A＝a（t）eiθ（t）/2，其中 a（t）和 θ（t）是均为时间变量 t的实函数，将其代入式（11），整理后分离方程的实部、虚部，便可得到冷连轧机振动系统在极坐标下的平均方程：

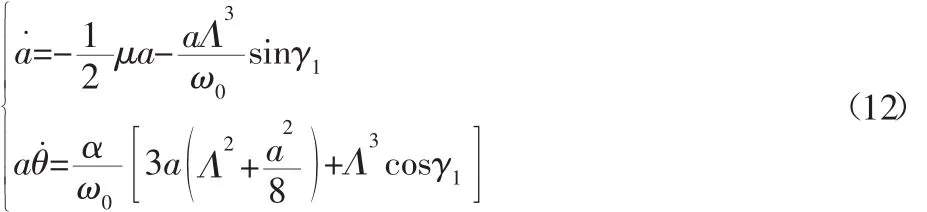
式中：γ1=σT1-θ，对于稳态响应有a˙＝θ˙=0，消去式（12）中的 θ可得动态轧制力下冷轧机系统超谐振动的幅频特性响应方程为：

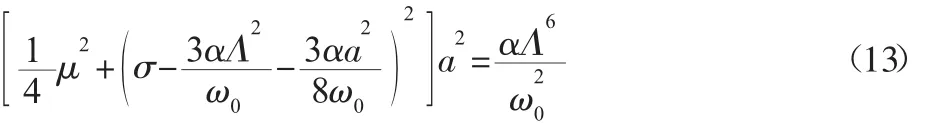
3.2 亚谐共振幅频特性方程

设ω与3ω0的差别为ε的同阶小量，即ω＝3ω0+εσ，σ为调谐参数，为了消除式（10）中的久期项，必须使：

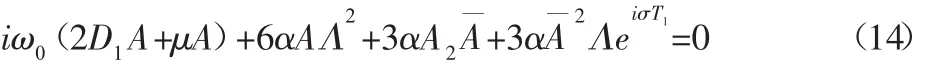
令 A=a（t）eiθ（t）/2，其中 a（t）和 θ（t）是皆为 t的实函数，将其代入式（14），并分离实部与虚部，可得到系统极坐标下的平均方程。

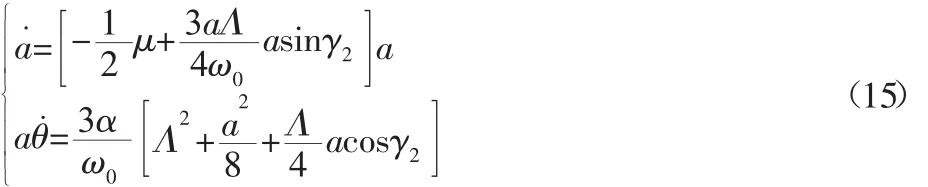
式（5）中 γ2=σT1-3θ，对于稳态响应有a˙＝θ˙=0，消去式（15）中的θ可得动态轧制力下冷轧机系统亚谐振动的幅频特性响应方程为：

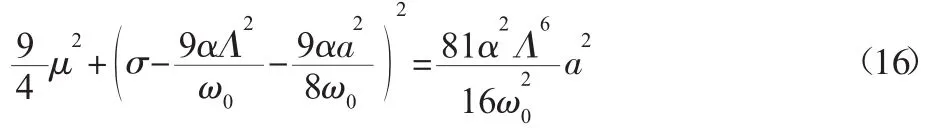
4 超亚谐共振特性分析

以某钢厂1780型冷连轧机的轧制参数为例，取如下近似值进行仿真计算，分别为：α=2.320，μ=1.225，ω=1.21，F=0.832。

不同轧制参数变化时的冷连轧机超谐共振幅频特性曲线，如图3～图5所示。由图3可知，随着F的增大，冷连轧机的振动区域、振动幅值变化较为微弱，可知外激力变化对系统的影响较小，这是由于动态轧制力适时调节，使轧机系统受到的外激力始终保持合适量值，从而避免轧机的剧烈振动，从而验证了动态轧制力这一概念的有效性。图4中，随着线性阻尼μ的增大，系统的振动幅值不断减小，同时振动区域也不断缩小，直至系统无振动现象发生，获得平稳运行，利于生产出高质量、高精度轧制产品。描绘了非线性刚度变化下的系统的超谐共振现象，如图6所示。随着参数的增大，共振区域和振幅同时增大，可见，动态刚度系数与动态轧制力组成的非线性参数项的波动对轧机系统的振动影响较大，在实际轧制过程中，要注意控制好这两项参数的量值，以保证冷连轧机的平稳运行。

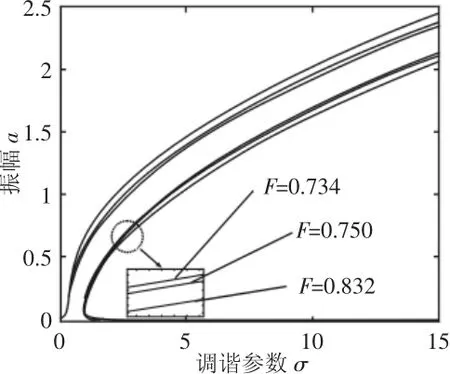
图3 外激力变化下的超谐共振幅频响应曲线Fig.3 The Curve of Super-Harmonic Vibration Amplitude-Frequency with Disturb Force

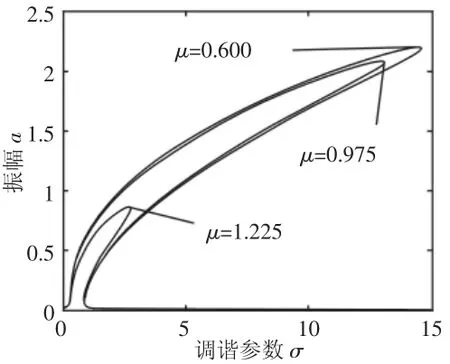
图4 线性阻尼变化下的超谐共振幅频响应曲线 Fig.4 The Curve of Super-Harmonic Vibration Amplitude-Frequency with Linear Damping

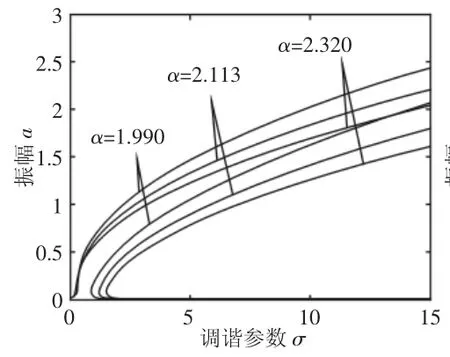
图5 非线性刚度变化下的超谐共振幅频响应曲线Fig.5 The Curve of Super-Harmonic Vibration Amplitude-Frequency with Nonlinear Stiffness

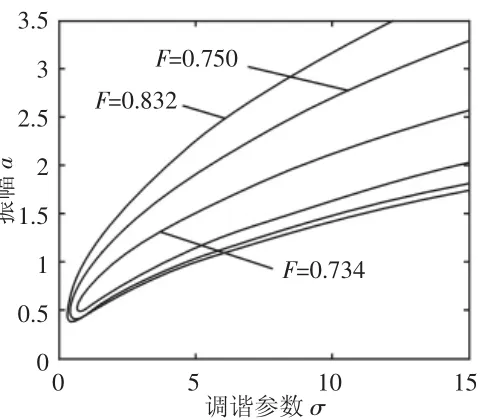
图6 外激力变化下的亚谐共振幅频响应曲线 Fig.6 The Curve of Sub-Harmonic Vibration Amplitude-Frequency with Disturb Force

描绘了含动态变化量的外激力、线性阻尼、非线性刚度发生改变时，冷连轧机出现亚谐共振现象的相应特性，如图6～图8所示。

图6中，随着外激力F的减小，振动幅值减小，共振区域缩小，但变化量较为微小，可见外激力对超谐、亚谐共振的影响一致。图7中，随着辊系间阻尼系数的减小，系统的振动幅值不断增大，同时共振区域也不断增大，但振动曲线的弯曲程度依然保持不变，即无跳跃现象发生，系统较为稳定。图8给出了非线性刚度变化下的亚谐共振幅频特性，随着α的减小，振幅和共振区域随之增大，且减小到一定值后，将出现跳跃和突变，使系统发生失稳。

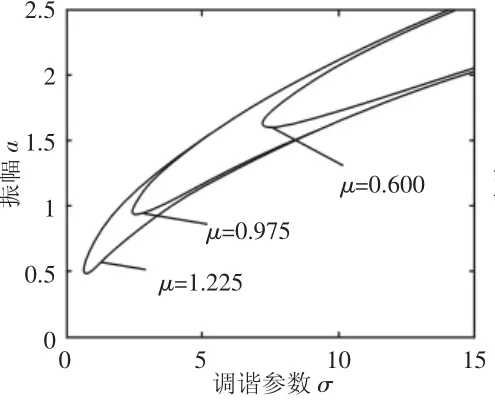
图7 线性阻尼变化下的亚谐共振幅频响应曲线Fig.7 The Curve of Sub-Harmonic Vibration Amplitude-Frequency with Linear Damping

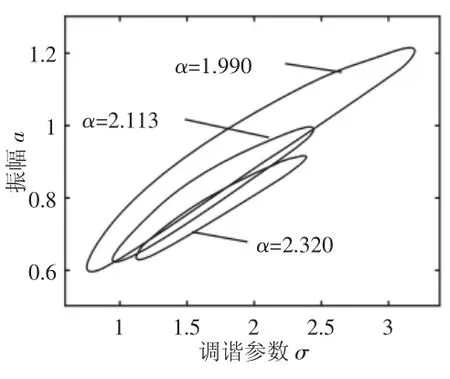
图8 非线性刚度变化下的亚谐共振幅频响应曲线Fig.8 The Curve of Sub-Harmonic Vibration Amplitude-Frequency with Nonlinear Stiffness

5 结语

（1）在引入较为接近实际轧制过程中存在动态轧制力的基础之上，建立了含机械结构、工艺参数以及周期性外激力的冷连轧机非线性振动动力学模型，使轧机振动模型更进一步接近实际振动状态，丰富了轧机振动模型。应用精度较高的多尺度法，得到了基于动态轧制力下的冷连轧机超谐共振和亚谐共振幅频特性方程。（2）以冷连轧机振动参数为例，仿真分析了不同轧制参数变化下的冷连轧机超谐、亚谐振动特性，从幅值、共振区域大小、骨干曲线偏移程度等方面给出了抑制轧机振动的措施与参数区域，为轧机平稳运行提供了理论参考。