基于径向基函数神经网络的白车身减重优化研究

兰凤崇 ，周建华 ，赖番结 ，陈吉清

1 引言

近年来，随着高性能计算机技术的不断发展和数值计算方法的深入研究，结构分析和优化技术日趋成熟，并逐渐应用到汽车各个设计阶段。以有限元方法为主体的汽车结构分析和轻量化设计，避免了设计的盲目性，减少设计成本，缩短汽车结构的开发周期，减轻了汽车结构重量。降低白车身质量是提高燃油经济型的重要途径，车辆每减重100kg，其每100km可节省燃油（0.3～0.5）L；车身占汽车总质量的（30～40）%，车身结构的轻量化具有重要意义。保证车身结构整体性能不降低的情况下，可最大限度地减轻车身各零件的质量。

目前国内外对于车身轻量化的研究广泛，由于白车身构成的板件较多，在优化设计时变量复杂，难以高效地进行减重设计。文献[1-2]采用基于灵敏度的近似方法构建NVH响应的Kriging近似模型，用序列二次规划法进行优化求解，收到了较好的减重效果。林涛等在概念设计开发阶段，基于灵敏度分析对某SUV车型进行轻量化设计，结果表明在质量不降低的情况下，整车扭转刚度有了较大的提升[3]。文献[4]在对比了多项式响应面与Kriging近似模型的基础上，建立了一种基于移动最小二乘的汽车正面碰撞响应面模型进行车身的轻量化研究。响应面、正交多项式和Kriging等近似方法都被普遍用在汽车结构的轻量化设计当中，采用的优化方法多以梯度优化和直接搜索等局部方法为主。鉴于此，在这里采用径向基函数神经网络的近似模拟方法，结合自适应模拟退火法的全局优化策略，对某白车身结构进行的减重优化设计。

在满足车身刚度和模态性能不降低情况下，通过灵敏度分析确定优化的结构件，以车身结构重量最小为目标，基于径向基函数神经网络近似模型进行自适应模拟退火法的全局最优化设计，最后通过原来有限元模型验证优化设计方案的可行性。

2 白车身静动态特性分析

通过有限元方法，可以预测车身结构的轻量化潜力，又可以对车身结构的各性能指标进行优化设计。

2.1 白车身有限元模型

白车身的结构主要是以板件为主，在有限元模型建立过程中，采用2D壳单元划分板件，网格单元尺寸为8mm；采用CWELD形式进行焊点单元的模拟；最后赋予各板件相应的材料属性。完成的白车身有限元模型，如图1所示。白车身总质量为364.89kg，网格数量为615579个，四边形网格数量为587497个，三角形数量为28082个，三角形网格占总数的4.56%。其他的网格质量指标均满足某企业分析的标准。

图1 有限元模型Fig.1 FEM Model

2.2 白车身刚度和模态性能分析

2.2.1 弯曲刚度

约束右前悬架固定座中心Z向平动自由度；约束左前悬架固定座中心Y向及Z向平动自由度；约束右后悬架固定座中心X向及Z向平动自由度；约束左后悬架固定中心三个方向平动自由度。在座椅R点位置分别施加沿-Z向1000N的集中力。

2.2.2 扭转刚度

约束后悬架固定座中心的六个自由度。在前左、右悬架固定座中心施加一对大小相等方向相反的垂向力，形成大小为3000N·m的扭矩。

2.2.3 模态性能

对白车身有限元模型进行自由模态分析，通过兰索斯法（Block Lanczos）提取特征值，得其一阶弯曲模态和一阶扭转模态值。通过相关有限元软件可以求得白车身的弯曲刚度为17218.2N/mm，扭转刚度为20032N·m/°，一阶弯曲模态为39.3Hz，一阶扭转模态为43.4Hz。

3 白车身静动态指标灵敏度分析

根据车身结构特点和生产工艺的相关制约，最终选定97个（关于车身对称平面呈对称分布的两个板件均按一个计算）车身板件的厚度作为优化变量，其厚度的变化范围为初始厚度的（±20）%或（±0.2）mm。利用有限元软件进行白车身重量、扭转刚度、弯曲刚度、一阶频率对板厚的灵敏度分析，不进行优化。本次的灵敏度分析通过计算目标函数对参与优化的板厚变量的某一点处的梯度数值，分析板厚变量对于目标响应的影响程度，通过分析灵敏度数值来确定最有效的参与优化的板件，灵敏度的梯度计算公式为：

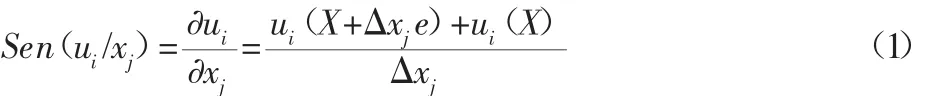
式中：X—设计参考点处参与优化的板件变量，Δxj—板件变量的变化值，数值大小是板件变量变化范围1%；e向量的维数和X一样。15个板件的扭转、弯曲和模态的灵敏度系数图，如图2所示。横坐标是板件编号，纵坐标是灵敏度值，通过计算分析，最后确定28个板件进行轻量化的优化设计。

图2 白车身相关性能指标灵敏度系数Fig.2 BIW Associated Performance Sensitivity Coefficient

4 基于径向基函数神经网络的白车身减重优化

白车身结构板件变量多，性能响应包括线性和非线性两种，采用基于近似模型的优化方法可提高设计效率[5]，可以快速地获得工程应用的指导值，缩短设计周期。本次应用的白车身优化策略流程图，如图3所示。

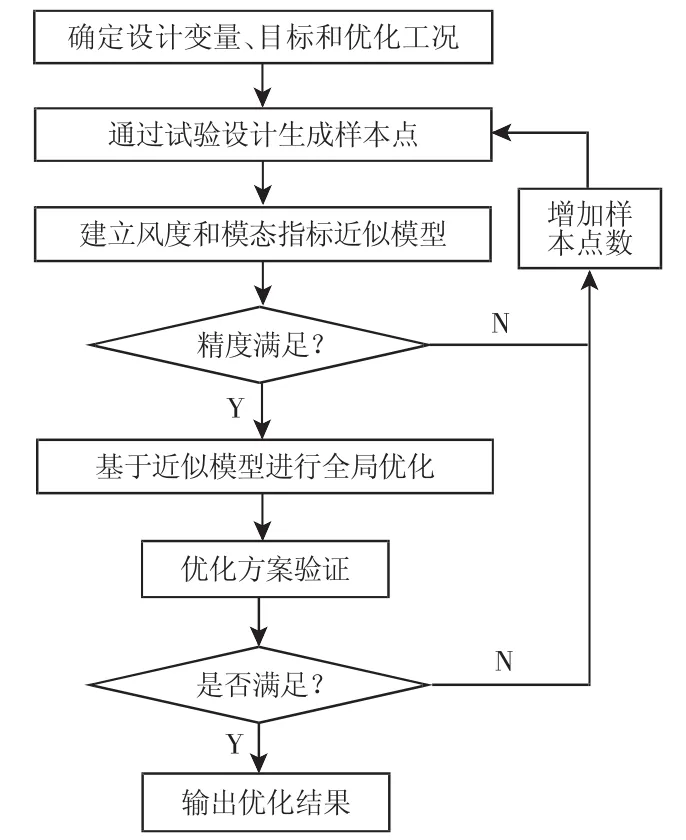
图3 白车身优化策略图Fig.3 BIW Optimization Strategy

4.1 径向基函数神经网络的基本理论

径向基神经网络是通过线性叠加构造出来的模型[6]，包括自变量和基函数两个因素，自变量是待测点和样本点之间的欧几里得距离，基函数是径向函数，其表达式为：

神经网络模型具有很强的逼近复杂非线性函数的能力，其无须数学假设，具有黑箱特点，学习速度快，具有较强的容错功能。克里格和径向基函数神经网络的效率都较高，但是在面对多变量问题时，克里格方法存在难以收敛的缺点。

4.2 白车身优化问题描述

实际工程中使用车身板件尺寸是离散的，在优化过程中也使用离散变量。对白车身这样一个复杂系统，其参与优化的设计变量多而且是离散变量集，约束函数多，直接采用传统的梯度优化或者直接搜索方法很难找到全局优化解。针对这一问题，采用改进的自适应模拟退火算法[7]（ASA，Adaptive Simulated Annealing），其比较擅长离散变量组合优化问题的极小值求解，能有效搜索全局优化解，具有较好的收敛性，求解效率高。以目标优化车型的质量最小化为目标，弯曲刚度、扭转刚度和一阶模态频率性能不下降为条件约束，建立确定性优化数学模型如下：

优化目标：min m（xi）

约束条件：KB（xi）≥17218.2N/mm

式中：m（xi）—白车身结构的质量函数；KB（xi）—弯曲刚度函数；KT（xi）—扭转刚度函数；f1（xi）—一阶频率函数，自变量是车身板件；xL、xU—参与优化板件的变化范围上下限；xi—参与优化的板件。

4.3 零件板厚的试验设计

根据灵敏度分析确定的28个优化设计变量，采用最优拉丁超立方试验法生成弯曲、扭转刚度以及模态性能的样本矩阵，共进行91次试验设计。最优拉丁超立方法具有有效的空间填充能力，试验次数为大于或等于因子数+1；能拟合非线性响应；产生的样本点随机且均匀分布的，而且每次分布的点都不一样[8]。部分设计变量的DOE矩阵，如表1所示。

表1 最优拉丁超立方试验设计矩阵Tab.1 Optimal Latin Hypercube Design Matrix

4.4 白车身静动态性能指标的近似模型

根据设计变量和优化工况的特点，弯曲、扭转刚度和模态近似模型采用径向基函数神经网络模型。每一种性能指标都以板件厚度为设计变量，且变量的许用取值范围都相同。为确定近似模型的精度，对其进行随机抽取样本点的误差分析方法，发现初步建立的近似模型达不到精度要求，经过一轮添加样本点后，建立的近似模型满足工程开发的精度要求，三个性能指标的误差分析结果，如图4所示。弯曲刚度的近似模型误差为4.9%，扭转刚度近似模型误差为0.7%，一阶模态的近似模型误差为1.6%，三个近似模型均可以用来进行白车身的优化设计。车身板件的密度是均匀的，对于以板厚为设计变量的质量函数是一阶函数关系，对应关系相对明确，质量指标的近似模型采用一次多项式拟合，进行了两次迭代满足了精度要求，模型的拟合精度很好，其近似函数如下：

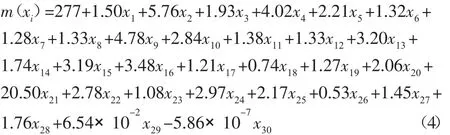
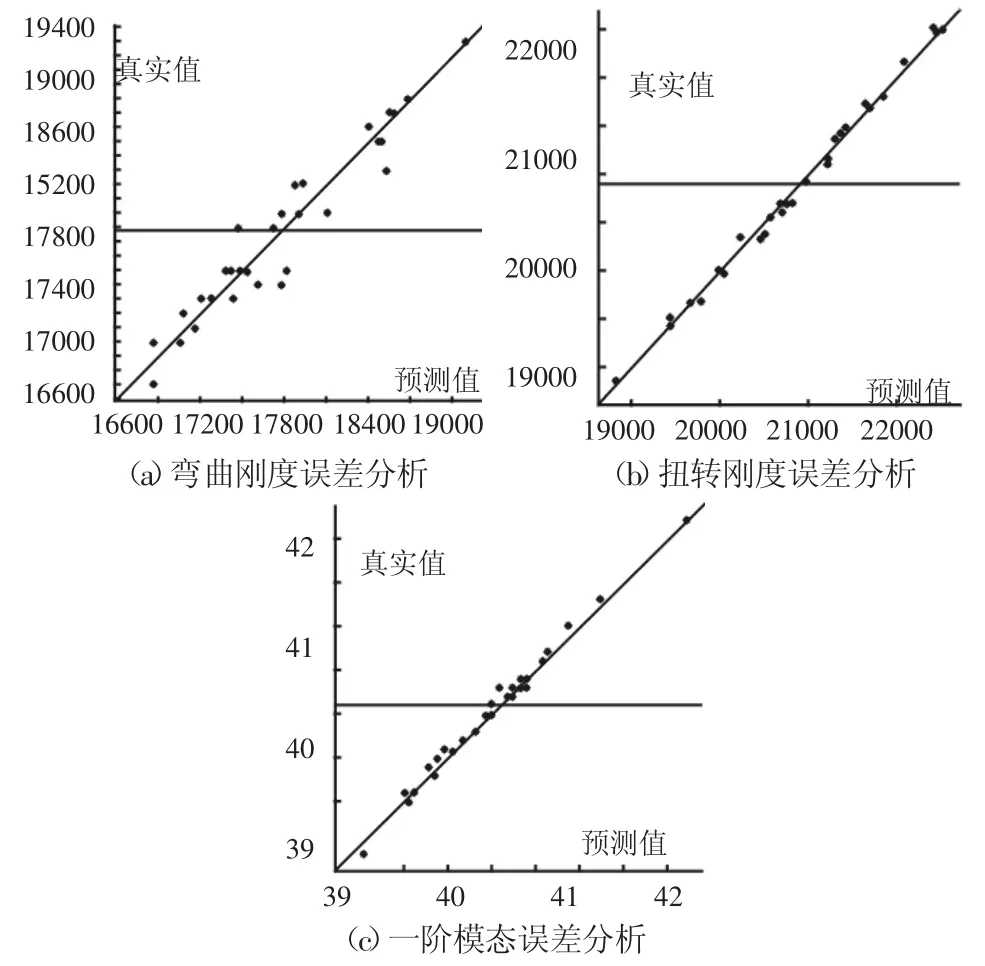
图4 刚度、模态指标真实值-预测值Fig.4 Actual-Predicted of Stiffness and Mode

4.5 优化结果分析

白车身优化设计问题中的设计变量都是离散变量，没有任何导数、梯度信息可供利用，采用全局优化的自适应模拟退火算法可以找到全局最优解。基于径向基函数神经网络模型，对优化数学模型进行全局寻优，求解程序经过1038次迭代计算，耗时2min左右，在第870次得到全局的最优解，其详细信息，如表2所示。优化过程中，具体的迭代信息，如图5所示。迭代图中出现的解集，包含满足约束条件的可行解、违反约束的解和推荐的最优解，推荐最优解指的是在同时满足三个约束条件的情况下，目标质量达到最小值。如果直接在原有的有限元模型上进行迭代优化求解，其计算时间会很漫长，而基于近似模型进行的优化效率非常高，需要付出的是构建近似模型时进行的试验设计分析和保证高精度的近似模型。根据优化结果，在白车身结构弯、扭刚度和模态值几乎不降低的情况下，减重20.89kg，占白车身质量的5.73%，减重效果明显。基于径向基函数神经网络模型得出的三个性能指标优化解，代入到原来模型求解，各个性能指标的误差不超过8%，其中弯曲刚度指标的误差最大，达到6.1%，误差均在可接受的范围之内。

表2 自适应模拟退火法优化解Tab.2 ASA Optimal Solution

图5 性能指标迭代求解过程Fig.5 History of Response

5 结论

针对目前的优化效率不高问题，结合设计变量的特点，提出了采用径向基函数神经网络方法构造白车身的刚度和模态指标的近似模型，并采用自适应模拟退火算法进行全局优化，最后得到的优化方案经原来有限元模型的验证，表明该设计方案具有可行性，重量减重效果达5.73%，结果也表明采用径向基函数神经网络模型模拟白车身的刚度和模态问题效果较好。对于白车身的减重优化，采用“灵敏度分析—试验设计—近似模型—全局优化”的优化策略，能够快速有效地获得全局的最优解，缩短优化设计周期，对白车身的优化设计具有指导性意义。