基于多导体回路法的牵引网电气参数计算研究

邓云川，刘志刚，黄 可，宋小翠，张桂南

(1．西南交通大学 电气工程学院， 四川 成都 610031；2. 中铁二院工程集团有限责任公司 电气化设计研究院， 四川 成都 610031)

随着电气化铁路向高速和重载化快速发展，我国电气化铁路面临全新的挑战和难题。准确实现电气化铁路牵引网的精确数学描述及电气参数提取是掌握牵引供电系统电气特性的前提。牵引供电系统存在多种供电方式：带回流线的直接供电方式、AT全并联供电方式等。上述牵引网系统均包括接触线、承力索和钢轨等多根导体，形成了复杂的电磁场结构和关系。

国内外学者利用多导体传输线理论对牵引网数学模型进行了大量研究。文献[1-2]针对交流电气化铁道的不同供电方式牵引网建立了统一复合链式电路模型。文献[3]采用多导体降阶法在电力系统电磁暂态仿真平台建立了牵引网谐波模型。文献[4]在推导和分析牵引网电磁特性的基础上提出了一种计算牵引网电抗参数的简易算法。文献[5]基于牵引网多导体传输线数学模型，给出了考虑回流电路影响时的接触网载流量计算方法。多导体传输线理论通常以回流导体作为参考导体计算单位长度参数。文献[6-7]分析了双导体传输线系统回路，推导出相应的单位长度外自电感。对于传输导体位于无限、理想导电平面上的情形，文献[8]以该导电平面作为回流导体的回路，采用镜像法推导出导体电容、电导和电感。文献[9-10]深入研究了大地平面上的单根传输导体在将大地作为回流导体时构成的回路阻抗计算，增加了校正项，并给出分析公式。一些学者在此基础上陆续做了大量拓展，包括计及大地和空气中的位移电流[11]、采用分层具有不同电气参数的大地结构[12]、以四周无限隧道模型代替半无限大平面计算隧道路段的牵引网参数[13-14]等。此外，为获得更精确牵引网多导体电气参数，不少学者也利用有限元法进行参数求解，求解对象包括接触线、钢轨、综合地线等[15-16]。但由于由牵引网参数组成的链式网络存在计算输入条件复杂、维度高等问题[1-3]，有限元计算并未得到广泛应用。

目前，牵引网多导体传输线模型普遍采用以简化Carson理论为基础的计算方法。该理论以大地作为参考导体，以此为基础开展计算。由于牵引供电系统是以接触线和承力索作为传输导体，回流线、钢轨、大地等作为回流导体构成的复杂多导体传输线系统，以大地作为参考导体构建的模型，容易被误解为大地成为所有导体的回流通道，导致对一些问题的认识和处理出现困难，如简化Carson理论虽能精确计算牵引网阻抗参数，但是难以直接获取各回路的电流分布，无法直接准确确定各导体载流能力。基于此，本文提出一种基于多导体回路法的牵引网电气描述和阻抗计算方法。考虑了包括大地在内的实际参与传输和回流的导体，将牵引网系统中导体按照传输和回流功能进行分类，由参与传输和回流的不同导体两两构造回路，并根据各回路的两导体半径和空间相对距离等参数计算出由各回路自阻抗和互阻抗构成的阻抗矩阵，据此推导各回路电流分配系数，进而得到系统综合阻抗。针对大地对架空回路的影响，开展相关研究。基于渝黔线的实际参数和渝利线的短路试验，通过经典Carson理论与多导体回路法的对比分析和试测验证了基于多导体回路法开展电气化铁路分析和计算的有效性。

1 多导体回路法的提出和理论推导

多导体传输线理论通常以回流导体作为参考导体计算单位长度电气参数，计算导体电感时采用的磁通为传输导体与回流导体间断面磁通。根据回路外自电感和互感的定义，互感不能脱离具体两个及以上相邻电路单独进行描述。通过扩展、延伸传输导体和回流导体可构建复杂的多导体回路系统。根据牵引供电系统的实际，牵引网系统可分为传输导体和回流导体数量相同的多导体回路系统(如直接供电方式)和传输导体和回流导体数量不相同的多导体回路系统(如带回流线的直接供电方式和AT牵引供电方式)。

为方便分析，基于多导体回路法的推导中均按无耗(不考虑电阻)考虑且忽略导体内自电感影响，即只考虑单一传输线导体的单位长度外自电感。

1.1 传输导体与回流导体数量相同的系统

以2传输导体并联、2回流导体并联的4导体4回路系统为例进行推导，多导体回路示意图如图1所示。图1中，D11、D12为传输导体，其电流为I11、I12；D01、D02为回流导体，其电流为I01、I02。D11与D01、D11与D02、D12与D01、D12与D02分别构成回路1～回路4。

根据各回路电压降与回路磁链的关系，可得当电源为正弦激励，各回路电压降、回路电感和各回路电流间的关系为

( 1 )

式中：lij(i=1,2,3,4；j=1,2,3,4)为回路1～回路4对应的自感和两两间的互感；ΔU1、ΔU2、ΔU3、ΔU4分别为回路1～回路4的电压降；I1、I2、I3、I4分别为通过回路1～回路4的电流。

表1 计及图1回路系统的参数

根据4条回路各自交联的磁链及各回路电流于其他回路交联的磁链，参考文献[6-7]，可推导得各条回路单位长度外自电感及其之间的互感lij(i=1,2,3,4；j=1,2,3,4)。根据表1参数，计算得到的回路自电感lii和互电感lij分别为

( 2 )

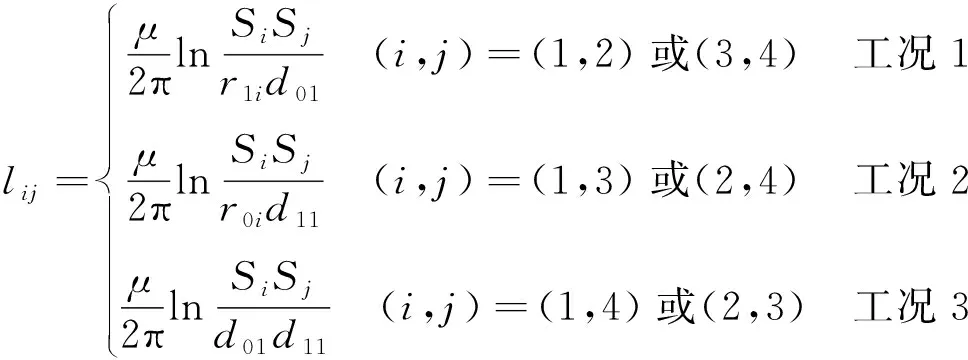
( 3 )

式中：μ为磁导率。

工况1即两回路共用一条传输导体且不共用回流导体的情况；工况2即两回路共用一条回流导体且不共用传输导体的情况；工况3即两回路既不共用一条传输导体也不共用一条回流导体的情况。

由于4条回路并联，这里假设I0为所有传输导体(或所有回流导体)的总电流。根据图1，有ΔU1=ΔU2=ΔU3=ΔU4=ΔU，I1+I2+I3+I4=I0，式( 1 )可转化为

( 4 )

假设ΔU=“1”，根据式( 4 )可得各回路电流为

( 5 )

假设k1、k2、k3、k4为4条回路的电流分配系数，显然，I1=k1I0、I2=k2I0、I3=k3I0和I4=k4I0。根据式( 5 )得到各回路电流分配系数k1、k2、k3和k4。

此外，基于图1，单位长度下各导体电流I11、I12、I01、I02与回路电流I1、I2、I3、I4的关系为式( 6 )，代入k1、k2、k3、k4即可获得各导体电流分配系数。

( 6 )

结合式( 1 )，将k1、k2、k3、k4分别代入回路1～回路4的单位长度压损计算公式，即

( 7 )

可求得回路1～回路4对应的等效单位长度综合电感l1、l2、l3、l4分别为

( 8 )

( 9 )

(10)

(11)

由于4条回路电压降相等，整合式( 7 )～式(11)可得单位长度等效电感l为

(12)

对于由n个传输导体和n个回流导体组成的由n×n条回路并联构成的复杂多导体系统情况，推导的单位长度下等效电感通用计算公式为

(13)

式中：n为传输导体(或回流导体)的个数；Sij为第i个传输导体与第j个回流导体间距离；r1j为第j个传输导体半径；r0j为第j个回流导体半径。

1.2 传输导体与回流导体数量不相同的系统

以2传输导体并联、3回流导体并联的5导体6回路为例，各导体位置分布如图2所示。图2中，D11、D12分别为传输导体，D01、D02、D03分别为回流导体，其对应的电流分别为I11、I12、I01、I02、I03。假设D11与D01、D11与D02、D11与D03、D12与D01、D12与D02、D12与D03构成的回路分别为回路1、回路2、回路3、回路4、回路5、回路6。

图2 2传输导体3回流导体位置示意图

基于图2，根据各回路电压降与各回路磁链的关系，当电源为正弦激励时，可得

(14)

式中：ΔU1、ΔU2、ΔU3、ΔU4、ΔU5、ΔU6分别为回路1～回路6的电压降，I1、I2、I3、I4、I5、I6分别为回路1～回路6的电流；lij(i=1,2,3,4,5,6；j=1,2,3,4,5,6)为6条回路对应的自感和两两间的互感，其计算参考式( 2 )、式( 3 )并根据图2所示系统布线情况获得。当各回路并联时，有ΔU1=ΔU2=ΔU3=ΔU4=ΔU5=ΔU6，I0=I1+I2+I3+I4+I5+I6。此时，D11、D12、D01、D02、D03电流与6条回路电流间关系为

(15)

图2中，由于回路电压降相等，其电流分配系数k1、k2、k3、k4、k5、k6参照式( 4 )、式( 5 )和k1=I1/I0、k2=I2/I0、k3=I3/I0、k4=I4/I0、k5=I5/I0、k6=I6/I0、k1+k2+k3+k4+k5+k6=1计算获得。结合式(15)的求解还可求得各导体电流分配系数。将电流分配系数分别代入回路1～回路6的单位长度压损计算公式，可得

(16)

基于式(16)，结合回路电感计算方法获得6条回路单位长度综合电感l1、l2、l3、l4、l5、l6。由于各回路电压降相等，则l1=l2=l3=l4=l5=l6。通过整合，得

(17)

对于由n个传输导体和m个回流导体组成的n×m条回路并联构成的复杂多导体系统情况，其等效单位长度电感通用计算公式为

(18)

式中：n为传输导体的个数；m为回流导体的个数。

2 大地对架空导体回路的影响分析

在第1章所述的基于多导体回路法的单位长度自电感和互电感推导中，回路可分为两类：导体与导体构成的架空导体回路；导体与大地构成的大地回流回路。考虑实际电气化铁道牵引网有部分回路只能铺设在大地上空，需要考虑大地对两种类型回路的影响。对于大地回流回路，大地作为回流导体，以地阻抗的形式反映了大地对该回路的影响；对于架空导体回路，当电流沿架空导线传播时，导线上电荷或电流源产生的电磁场会入射到地面上，如果大地为良导体，其土壤电导率为无限大，则大地的反射系数为单位1，入射的电磁场会在地面处完全反射，不会穿透到土壤里，此时，大地对架空导体回路不会产生影响，而实际土壤电导率不可能为无限大，因此，有必要就大地对架空导体回路的影响进行分析。

图3 计及位于大地上双导体的Dubanton线路等值电路

如图3所示，架空导体i和架空导体j构成回路，两导体位于大地平面上。图3中，ri、rj分别为导体i和导体j的等值半径；dij为导体i和导体j的距离；hi、hj分别为导体i、导体j与大地间的距离；Dij为导体i与导体j镜像地回流导体间的距离；p为地中复深度；Dij'为导体i与导体j复深度地回路间的距离。基于图3，根据第1章所述的架空导体回路法得到的i-j回路自电感Lij为

(19)

目前，对以大地作为回流导体的回路单位长度阻抗计算，Carson理论是普遍使用的方法。广泛采用的、用于计算回路自阻抗和互阻抗的简化Carson公式[10, 17]]和计及地中涡流影响的Dubanton公式[17-18]分别为

(20)

(21)

为分析大地的影响，这里虚拟了架空导线i和j均通过大地构成回路。假设导体i与大地构成的回路电流为I，导体j与大地构成的回路电流为-I，这样构成的回路与导体i和导体j构成的回路是等效的。根据高斯定律，i-j空间磁链Ψij等于i-大地空间磁链Ψig与j-大地空间磁链Ψjg之和，即

Ψik=Ψig+Ψjg=I(Lig+Ljg-2Mig-jg)

(22)

(23)

式(23)与式(19)的计算结果完全一致。可见，采用简化Carson公式时大地对架空导体回路影响完全抵消。

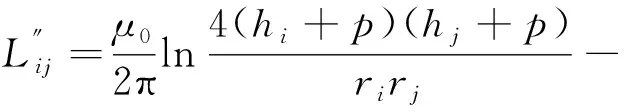
(24)

按照上述公式开展实例计算分析，假设ri为0.007 2 m，rj为0.012 8 m，导体i、导体j的直流电阻分别为0.015 97 Ω/m、0.135 0 Ω/m，土壤电阻率ρ为100 Ω·m。考虑到电气化铁路牵引供电系统各导体间水平和垂直距离基本不超过10 m，导体间水平距离范围设定为0～10 m，垂直距离范围设定为0.1～10 m。通过计算，可得工频下(50 Hz)的基于架空回路阻抗法和Dubanton公式的综合阻抗计算结果，见表2。

根据表2，两种方法计算的电阻最大相差1.21×10-5Ω/km，占回路电阻的0.004 1%；电抗最大相差1.71×10-7Ω/km，占按架空回路法计算结果的0.000 018 66%。因此，工频下大地对架空导体回路的影响较小，可以忽略不计。

表2 计及工频的架空回路法和Dubanton公式计算对比结果

随着频率增加，大地对架空导体回路影响有所增加，由于牵引供电系统负荷频率基本小于2 kHz，因此，按照f=2 kHz进一步分析计算。基于架空导体回路法和Dubanton公式法，得到的单位长度电抗对比结果如图4所示，两者误差如图5所示。

图4 计及2 kHz的架空回路法和Dubanton公式计算对比

图5 计及2 kHz的架空回路法和Dubanton公式计算差值

根据图4和图5，当频率为2 kHz时，采用架空回路法计算得出单位长度电抗和考虑大地影响的Dubanton计算公式得出的结果相差较小，最大偏差仅0.004 195%。基于架空回路法得到的最大单位长度电抗为36.646 3 Ω/km，基于Dubanton公式得到的最大单位长度电抗为36.644 7 Ω/km，单位长度电阻减少0.001 6 Ω/km，占回路阻抗的0.043 66%。因此，采用架空回路法计算得出的单位长度电抗和电阻，能够满足电气化铁路牵引供电系统计算和分析的需要。

3 实际线路验证

3.1 多导体回路法与Carson理论对比分析

基于渝黔线实际线路，根据牵引供电系统各导体半径及位置分布，分别利用Carson理论和本文提出的多导体回路法对牵引网综合阻抗进行计算。其中，渝黔线牵引网采用带加强线的直接供电方式，参与传输和回流导体包括承力索、接触线、加强线、两条钢轨和大地，其横截面位置分布如图6所示，相应传输导体、回流导体及其构成的回路编号见表3。

图6 基于渝黔线实际线路横截面的导体位置分布(单位：mm)

导体名称钢轨1钢轨2大地接触线123承力索456加强线789

表4为渝黔线实际线路的各导体电气参数。对于大地等值半径及导线-地回路等值深度而言，采用式(25)进行计算。

(25)

式中：Dg单位为cm；σ为大地电导率；f为频率，本文取工频50 Hz。由于大地电导率与天气、土壤特性等因素均有关，当大地电导率σ具体值无法精确确定时，采用普遍值，即930 m[16]。

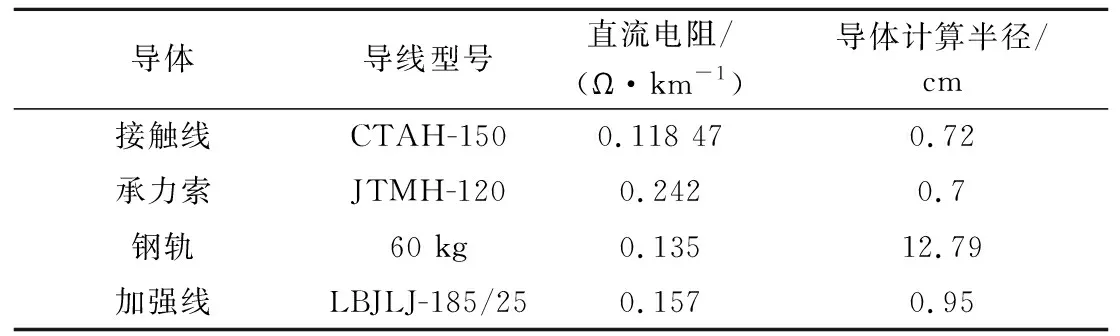
表4 渝黔线各导体电气参数

此外，根据如图6所示的渝黔线各导体间水平与垂直距离，通过计算可得接触线与承力索间、接触线与加强线间、承力索与加强线间的距离分别为1.3、4.248 9、4.002 2 m；两根钢轨间、钢轨1与大地间、钢轨2与大地间距离分别为1.435、930、930 m；接触线与两根钢轨间、接触线与大地间、承力索与两根钢轨间、承力索与大地间、加强线与钢轨1间、加强线与钢轨2间、加强线与大地间距离分别为6.042 7、930、7.335 2、930、8.803 7、8.125 5、930 m。显然，渝黔线回路系统属于传输导体与回路导体数目相同的多传输导体多回流导体系统。基于此，若不忽略渝黔线各导线的电阻，利用1.1节所示方法计算渝黔线单位长度阻抗，获得的单位长度综合阻抗为(0.076 8+j0.294)Ω/km。

利用Carson理论对计及电阻的渝黔线实际线路阻抗进行计算，使用软件为TENICO，其界面如图7所示。基于图6和表4，将渝黔线实际线路参数输入至TENICO计算界面中，线路单位长度综合阻抗运行结果为(0.076 917+ j0.293 33)Ω/km。因此，利用多导体回路法的推导结果(0.076 8+ j0.294)Ω/km与按经典Carson公式的计算结果基本一致。

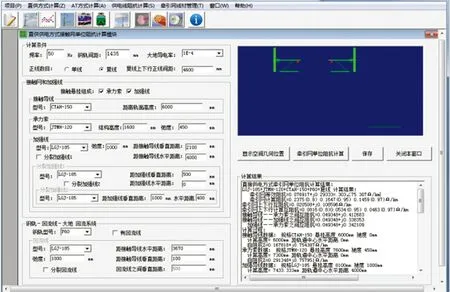
图7 TENICO软件界面

此外，用多导体回路法推导阻抗过程中得到的各回路电流分配系数，见表5。其中，接触线、承力索和加强线的电流分配系数分别为0.336 3、0.296 1和0.367 6；钢轨和大地的电流分配系数分别为0.553 4和0.446 5。显然，接触线和加强线在传输线中所占电流分配比例较大，钢轨在回流线中所占电流分配比例较大，符合牵引供电系统实际情况。鉴于经典Carson公式难以直接获取各回路电流分布，本文所述方法在牵引供电系统的描述上有较好的优越性。

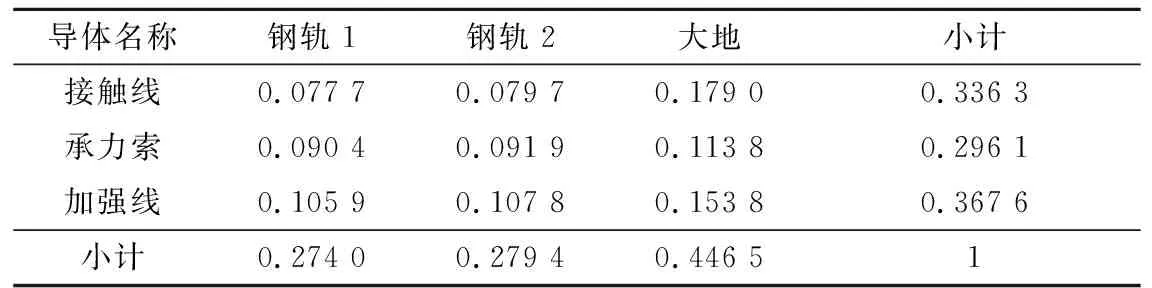
表5 基于多导体回路法所得渝黔线各回路电流分配系数

3.2 试验验证

基于渝利线丰石臂实际线路开展试验以验证多导体回路法的可信性。图8为渝利线实际线路横截面的各导体位置分布。试验验证分两部分，一是丰石臂末端短路分开供电试验，二是丰石臂首端短路迂回供电试验；其电路示意图分别如图9(a)和图9(b)所示。渝利线为带回流线直接供电方式复线电气化铁路，表6为渝利线牵引网各导体参数。如图9所示，牵引网系统由完全对称相等的上行和下行系统构成，上行或下行承力索、接触线构成传输导体；钢轨、回流线、综合地线和大地构成回流导体。其中上行或下行承力索与两根钢轨间、承力索与大地间、承力索与回流线间、承力索与综合地线间、接触线与两根钢轨间、接触线与大地间、接触线与回流线间、接触线与综合地线间的距离分别为8.08、930 m(等值深度)、3.779 2、9.675 5、6.487 9、930、3.400 4、8.420 7 m。此外，各导体的计算半径和位置见表6(各导体所在坐标均以图8中钢轨1与钢轨2的中点为原点)。

图8 基于渝利线实际线路横截面的各导体位置分布(单位：mm)

图9 渝利线丰石臂短路试验电路

基于图9(a)开展带回流线直接供电方式分开供电的短路实验(K1、201与291断开，K2与202合闸，下行末端短路)，在牵引变压器次边处采集供电臂首端电压U(牵引变电所低压侧母线电压)，开关202电流互感器处采集电流I。实验所测U为17 941 V，I为2 186.8 A，阻抗角72.8°。由于供电臂长度24.8 km，可得该供电方式下线路单位长度阻抗为(0.098+j0.315 9)Ω/km，而采用多导体回路法推导结果为(0.074 7+j0.301 2)Ω/km，两者电感结果非常接近。

基于图9(b)开展带回流线直接供电方式迂回供电的短路实验(K1、201断开，K2、202与291合闸，上行首端短路)，在牵引变压器次边处采集供电臂首端电压U(牵引变电所低压侧母线电压)，开关202电流互感器处采集电流I。实验所测U为20 429 V，I为1 660 A，阻抗角为71.1°。由于迂回供电臂长度为49.6 km，可得该供电方式下线路单位长度阻抗为(0.080 5+j0.234 7)Ω/km，采用本文多导体回路法推导结果为(0.071 9+j0.233 2)Ω/km，两者的电感结果也较接近。

此外，针对图9(a)和图9(b)所示的两种短路实验，在基于多导体回路法推导过程中获得的电流分配系数见表7。由表7可知，传输导线的电流分布中接触线所占比例较大，回流导线的电流分布中钢轨所占比例最大，回流线其次，综合地线和大地所占比例相对最小。符合带回流线直接供电方式牵引供电系统实际情况。

表6 基于渝利线牵引供电系统的各导线主要参数

表7 基于渝利线牵引供电系统电流分配系数计算结果

综合分析，由于理论计算中没有考虑传输导体与回流导体间的过渡电阻，导致理论计算与实测结果电阻值偏差较大，而过渡电阻主要由短路点处的电弧电阻以及牵引变电所处的接地电阻构成。

对于短路点的电弧电阻，按照参考文献[19]，通用的电弧伏安特性可表示为

(26)

式中：Ea为单位长度的电弧电压；k和α为常数。对于大气中电弧，当电流I≤100 A时，k=60～80，α=0.5；当电流I>100 A时，k=10～20，α=0。

由于短路试验测量得到的电压和电流值是通过牵引变电所27.5 kV母线的电压互感器和馈线断路器的电流互感器测得，从整个测量回路分析，回路阻抗除了包括牵引网阻抗外，还包括牵引变电所接地电阻。目前，牵引变电所接地电阻按照低于0.5 Ω进行控制，经现场调查，该牵引变电所接地电阻为0.4 Ω。

考虑电弧电阻和牵引变电所接地电阻，基于图9(a)所示带回流线直接供电方式分开供电计算结果为(0.092 2+j0.301 2)Ω/km；基于图9(b)所示带回流线直接供电方式迂回供电计算结果为(0.080 9+j0.233 2)Ω/km，与实测结果非常接近。

4 结论

准确获取牵引网电气参数是研究牵引供电系统性能的基础，基于牵引供电系统存在多条回流通道实际情况，本文提出一种基于多导体回路法的牵引网阻抗计算方法，不仅较为精确计算牵引网综合阻抗，还反映了牵引网各导体电流分布关系。

(1) 根据牵引供电系统的实际，可将包括大地在内的牵引网系统中导体按照传输和回流功能进行分类：传输导体与回流导体数量相等的多导体回路系统和传输导体与回流导体数量不等的回路系统。对于每一类系统，基于各回路自阻抗以及不同回路间互阻抗的求解可以推导出各回路电流分配系数和牵引网系统综合阻抗。

(2) 牵引网回路可以分为位于大地上的、导体与导体构成的架空导体回路和导体与大地构成的大地回流回路。对于后者，大地作为回流导体以地阻抗的形式反映了大地对该回路的影响；对于前者，本文基于多导体回路法，将架空导体回路法计算的阻抗、简化Carson公式及Dubanton公式计算阻抗进行对比分析，发现大地对架空导体回路的影响微乎其微，正常情况下采用架空回路法得到的牵引网阻抗能满足电气化铁路牵引供电系统计算和分析的需要。

(3) 针对牵引网线路单位长度综合阻抗，基于渝黔线线路的实际参数，通过计算对比验证了多导体回路法与Carson公式推导结果的一致；利用渝利线丰石臂实际线路的末端短路分开供电试验和该供电臂首端短路迂回供电试验验证了基于多导体回路法开展电气化铁路分析和计算的有效性。