轴向温度力影响下周期离散支承钢轨竖向振动特性分析

冯青松，汪 玮，刘庆杰，雷晓燕

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013)

无缝线路减少了钢轨接头数量，提高了列车运行舒适性及平稳性。无缝线路中的钢轨不能自由伸缩，当钢轨温升或温降幅度(实际轨温与锁定轨温差值)过大时，钢轨内部将产生较大的轴向温度力，极易造成无缝线路胀轨跑道或钢轨折断，危及列车的运行安全。因此，采用合适方式检测无缝线路钢轨温度力的变化情况是铁路工务部门日常养护维修中关注的课题之一。

目前，无缝线路温度力的检测方式主要包括有损检测、半有损检测以及无损检测。其中，有损及半有损检测方式主要有锯轨法、钻孔法以及横向加力法,此类检测方法在检测过程中会对既有轨道结构的稳定性造成破坏，故只在早期使用且应用范围不广。无损检测方式主要包括观测桩法、标定轨长法、巴克豪森法、X射线法以及超声导波法。观测桩法和标定轨长法是早期的无缝线路温度力检测方式，其主要缺陷是检测过程中人为因素影响较大，检测结果精度不高。巴克豪森法、X射线法以及超声导波法作为近年提出的无损检测方法，其不足之处是只能检测钢轨表层或浅表层范围内的温度力，不能反映整个钢轨截面的受力状态，钢轨内部存在伤损时检测结果的准确性尚未得到验证。此外，近年来还有一些轨温及温度力的在线监测方式，如光纤传感器法等，这些在线监测方式在检测前需明确线路的锁定轨温，现实中受现场条件制约，无缝线路实际锁定轨温一般不等于线路的设计锁定轨温，目前还没有较精确的测得无缝线路实际锁定轨温的方法。另外，我国共有十多万公里的无缝线路，若大范围使用在线监测技术，检测成本将大幅提高。

由结构振动理论可知，内部存在纵向力时，梁的振动特性(如自振频率等)会发生改变。利用这一结构振动原理，可为钢轨内部温度力的检测提供一种可能途径。近年来，专家学者开始了这方面的研究。传统轨道结构振动特性分析中，通常只考虑竖向荷载作用[1-10]，结合轴向温度力的研究较少。文献[11-14]通过运用有限元方法，并结合Timoshenko梁在理论上分析轴向温度力影响下的钢轨在低频范围内(0～100 Hz)的振动特性。由于低频范围内钢轨共振频率随轴向温度力的变化不明显，需拆除一定数量的扣件，使轨枕间距达到8.4 m以提高共振频率对温度力的敏感程度。文献[15]建立了有砟轨道的三维梁单元模型，通过周期结构理论以及Floquet变换方法分析轨道结构频散特性与温度力的关系，但建模及分析过程比较复杂。

本文根据无缝线路轨道结构特点，将钢轨考虑为无限长弹性梁，轨下支承结构等间距布置。通过周期结构波数有限元理论建立轴向温度力影响下轨道结构的周期支承梁模型，分析轴向温度力影响下周期支承钢轨在0～5 000 Hz范围的振动特性，并探讨轨枕间距对振动特性的影响。

1 轴向温度力影响下周期离散支承钢轨的频散及位移方程

1.1 周期支承结构位移响应及频散方程

根据周期结构波数有限元方法，荷载作用时的周期离散支承弹性体运动微分方程为[16]

( 1 )

式中：M、K0、K1、K2均为常数矩阵；P(x,t)为作用于弹性体上的荷载；q(x,t)为截面上n个节点的位移响应，每个节点的位移均由三个方向的位移分量表示，即沿x方向的位移响应u、沿y方向的位移响应v和沿z方向的位移响应w。因此q(x,t)可表示为

( 2 )

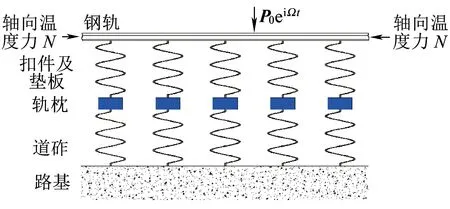
图1 轴向温度力作用下轨道结构周期离散支承梁模型

对于图1所示的周期离散支承轨道结构，作用于钢轨上的荷载由两部分构成，即外荷载Pe(x,t)和轨下支承结构提供的支承力Ps(x,t)。当作用于弹性体上的外荷载为移动谐荷载时，Pe(x,t)可表示为

Pe(x,t)=δ(x-x0-ct)P0eiΩt

( 3 )

式中：δ(·)为Dirac函数；x0为荷载的初始作用位置；c为荷载移动速度；P0为谐荷载幅值；Ω为谐荷 载圆频率。

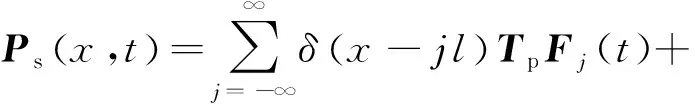
( 4 )

设弹性体在外荷载Pe(x,t)以及支承力Ps(x,t)作用下的位移响应分别为qe(x,t)和qs(x,t)。根据线性叠加原理，弹性体在荷载作用下的位移响应可表示为

q(x,t)=qe(x,t)+qs(x,t)

( 5 )

式中：qe(x,t)，qs(x,t)满足

( 6 )

将式( 3 )及式( 4 )代入式( 6 )中，并做傅里叶变换，可得弹性体在荷载作用下的位移响应表达式为

( 7 )

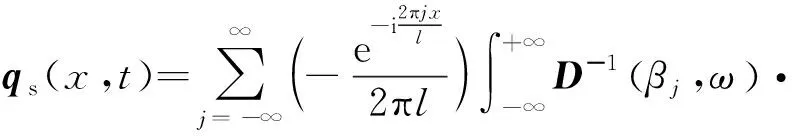
( 8 )

式中：

D(β,ω)=-ω2M+K0+iβK1+β2K2

( 9 )

ω=Ω-βc

(10)

(11)

(12)

式( 7 )与式( 8 )之和即为周期离散支承弹性体在移动谐荷载作用下的位移响应。

根据弹性体在荷载作用下的位移响应求解表达式可知，对于周期离散支承弹性体，要使其自由振动存在，则有

(13)

式中：H(ω)为支承结构的动力柔度矩阵[17]，该表达式即为周期离散支承弹性体的频散方程。

1.2 轴向温度力影响下周期支承钢轨动力学方程

将图1模型中的钢轨考虑为Timoshenko梁，轨枕考虑为质量块，轨下支承结构(扣件及垫板、轨枕和道砟)对钢轨的支承作用通过动力柔度矩阵模拟。温度应力考虑为集中力作用，同时不考虑梁截面变形。轴向温度力作用下周期离散支承钢轨竖向振动的运动微分方程可表示为

(14)

式中：ρ为钢轨密度；A为钢轨横截面积；w为钢轨的竖向位移响应；N为轴向温度力，以压为正；κ为截面剪切系数；G为钢轨的剪切模量；θ为截面的转角；I为钢轨截面惯性矩；E为钢轨弹性模量；P0为竖向荷载幅值。由于支承结构提供的支承弯矩对钢轨竖向振动特性的影响较小，分析中该部分的影响可以忽略不计[17]。将式(14)用周期结构波数有限元方法表示，则有

(15)

式中：kbv为道砟竖向刚度；kpv为扣件及垫板竖向刚度；ms为轨枕质量；bs为轨枕宽度；ω为钢轨圆频率。钢轨、扣件及道砟的刚度采用复阻尼形式，考虑各自的损失因子。

2 模型验证

本章主要分析无轴向温度力影响时周期离散支承钢轨的频散曲线，以及在单位固定谐荷载作用下荷载作用点处的位移幅值曲线。为方便结果比对，分析中选用的轨道结构参数与文献[17]一致。其中，钢轨采用UIC60钢轨，扣件及垫板、轨枕及道砟等轨下部件的材料参数见表1，考虑轨道结构的对称特性，取半结构分析，轨枕间距为0.6 m，轴向温度力N=0，外荷载为单位固定谐荷载。

表1 钢轨及轨下部件的参数取值

由式( 5 )～式(15)可得周期离散支承钢轨的频散曲线及跨中作用单位固定谐荷载时荷载作用点处的位移幅值曲线，如图2(b)、图3(b)所示。将结果与文献[17]中的分析结果对比，可以看出两者具有较好的一致性。

图2 周期离散支承钢轨频散曲线

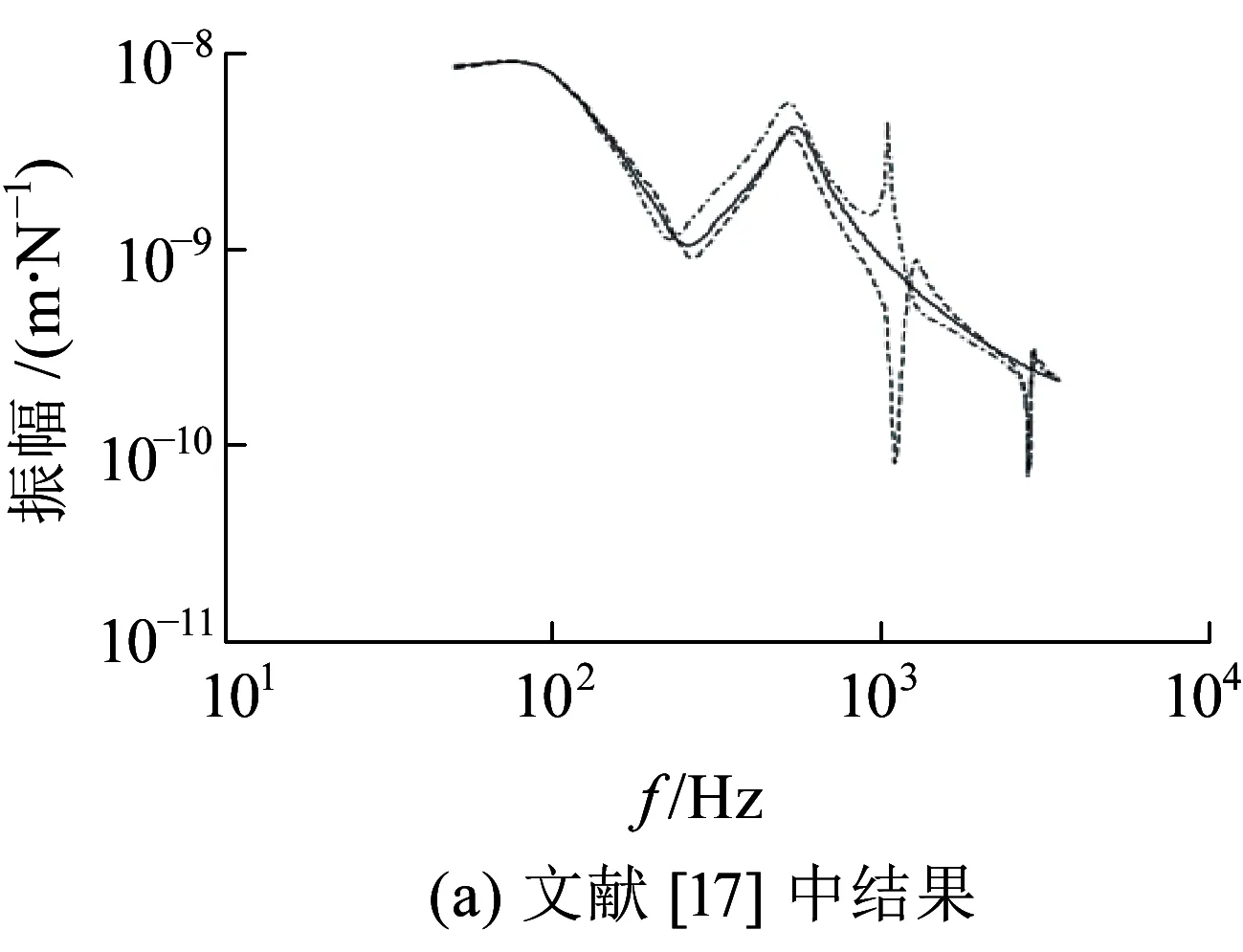
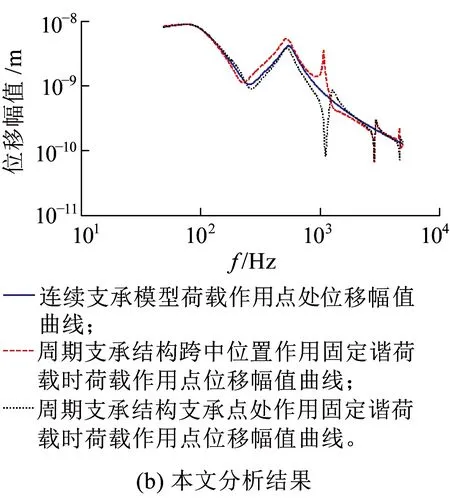
图3 周期支承钢轨荷载作用点处的钢轨位移幅值曲线

图3分析比较了单位固定谐荷载作用下连续支承模型和周期离散支承两种模型在荷载作用处的钢轨位移幅值曲线。从图3可以看出，当分析频率在1 000 Hz以下时，周期离散支承模型与连续支承模型得到的分析结果基本一致；当分析频率高于1 000 Hz时，采用周期离散支承模型能够得到相应的共振频率，连续支承模型则无法得到。因此，对于有砟轨道，当分析频率低于1 000 Hz时，建议采用计算效率较高的连续支承模型分析轨道结构的振动特性较合适，当分析频率高于1 000 Hz时，采用周期离散支承模型更合适。

图4为周期离散支承钢轨跨中作用单位固定谐荷载时荷载作用点处的钢轨位移幅值曲线。从图4可以看出，在分析频率0～5 000 Hz内，周期离散支承钢轨共存在5阶共振频率，即图中标示的共振频率A(80 Hz)、C(527 Hz)、D(1 080 Hz)、G(2 947 Hz)及H(4 675 Hz)。其中，共振频率D及H分别为周期离散支承钢轨前两阶pinned-pinned共振频率。由于共振频率点处钢轨位移幅值曲线均存在较明显的峰值，易于识别，因此，本文将共振频率A、C、D、G及H作为分析指标，探讨轴向温度力及轨枕间距变化对共振频率的影响。

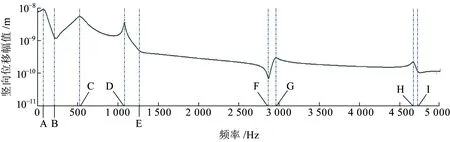
图4 周期离散支承钢轨跨中作用单位固定谐荷载时跨中的钢轨位移幅值曲线

3 轴向温度力影响分析

梁的两端作用轴向温度力时，其振动特性(如结构的共振频率)将会发生改变。本章根据无缝线路钢轨在使用过程中可能出现的温升或温降幅度，确定相应的温度力幅值，分析内部轴向温度力变化对钢轨共振频率的影响。温升幅度及温度力幅值的取值见表2，温度力幅值以拉为正。分析中钢轨为UIC60钢轨，轨枕间距为0.6 m，各部件的材料参数与表1一致。

表2 无缝线路钢轨温升幅度与温度力对应关系

图5为周期离散支承钢轨竖向振动共振频率与轴向温度力之间的变化关系。从图5可以看出，周期离散支承钢轨竖向振动各阶共振频率均随轴向温度拉力的增加而增大，随轴向温度压力的增加而减小。此外，根据图5(f)可以看出，共振频率越大，其受轴向温度力的影响越明显；共振频率D、G及H受轴向温度力的影响最明显，其平均变化率分别约为0.098、0.14、0.21 Hz/℃，即当轨温变化约为10、7和5 ℃时，共振频率D、G、H的频率变化幅度为1 Hz。因此，可以将共振频率D、G、H作为无缝线路钢轨内部温度力大小的主要评价指标。

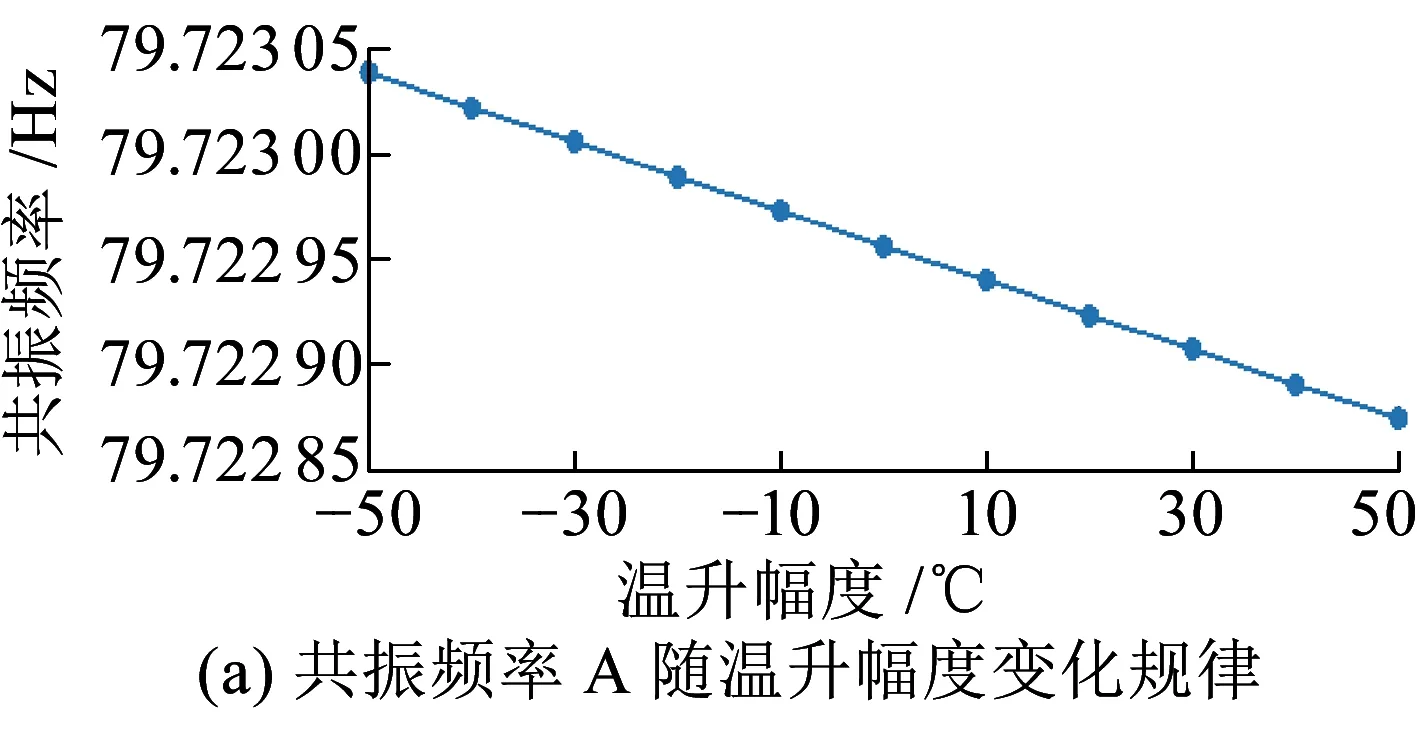
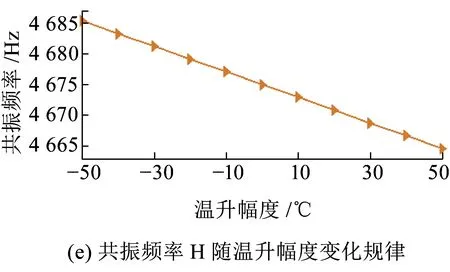
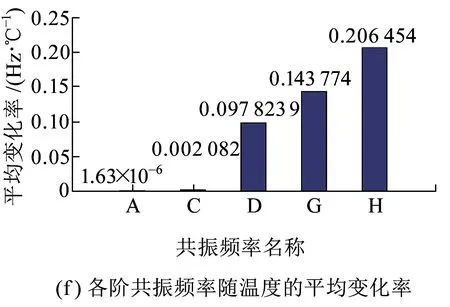
图5 周期离散支承钢轨竖向振动各阶共振频率随温升幅度变化规律及平均变化率

4 轨枕间距影响分析

轨枕间距对轨道结构振动特性有较大影响。有砟轨道的部分维修作业(如捣鼓、换枕)，会不可避免地对原有轨枕布置产生一定的影响。因此，分析不同轨枕间距条件下，轴向温度力对周期离散支承钢轨竖向各阶共振频率的影响是必要的。分析中，轨枕间距取值为0.55～0.65 m。无缝线路钢轨内部温度力取值同表2。钢轨及轨下支承结构的材料参数取值同表1。

图6(a)、(c)、(e)、(g)、(i)为不同温升幅度下，轨枕间距变化对周期离散支承钢轨各阶共振频率的影响。从图6可以看出，周期离散支承钢轨竖向振动各阶共振频率均随轨枕间距的增加而减小，且共振频率越大，轨枕间距对其影响越明显。图6(b)、(d)、(f)、(h)、(j)为不同轨枕间距下共振频率随轴向温度力的平均变化率，当轨枕间距为0.60 m时，共振频率A、C、D、G、H随钢轨温升的平均变化率分别为1.63×10-6、2.1×10-3、0.098、0.144和0.205 Hz/℃。分析频率低于1000Hz时，周期离散支承钢轨的共振频率(A、C)随轴向温度力的平均变化率随轨枕间距的增加而增大；分析频率高于1 000 Hz时，周期离散支承钢轨的共振频率(D、G、H)随轴向温度力的平均变化率随轨枕间距的增加而减小。可见钢轨共振频率随温度力的变化关系受轨枕间距的影响较大，采用振动方法分析无缝线路钢轨内部温度力时需先确定轨枕间距。

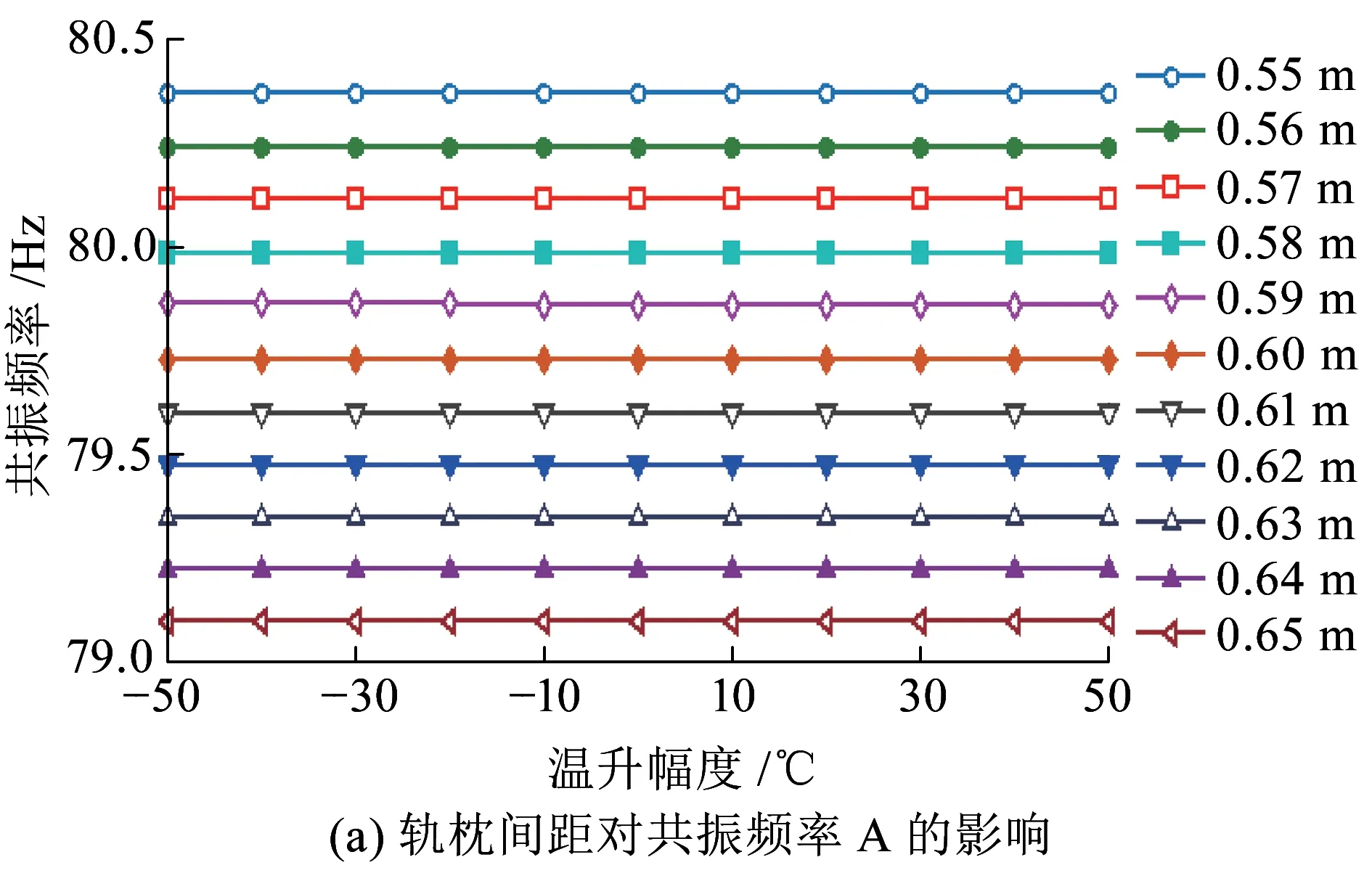
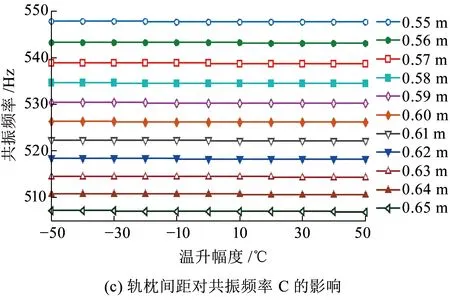
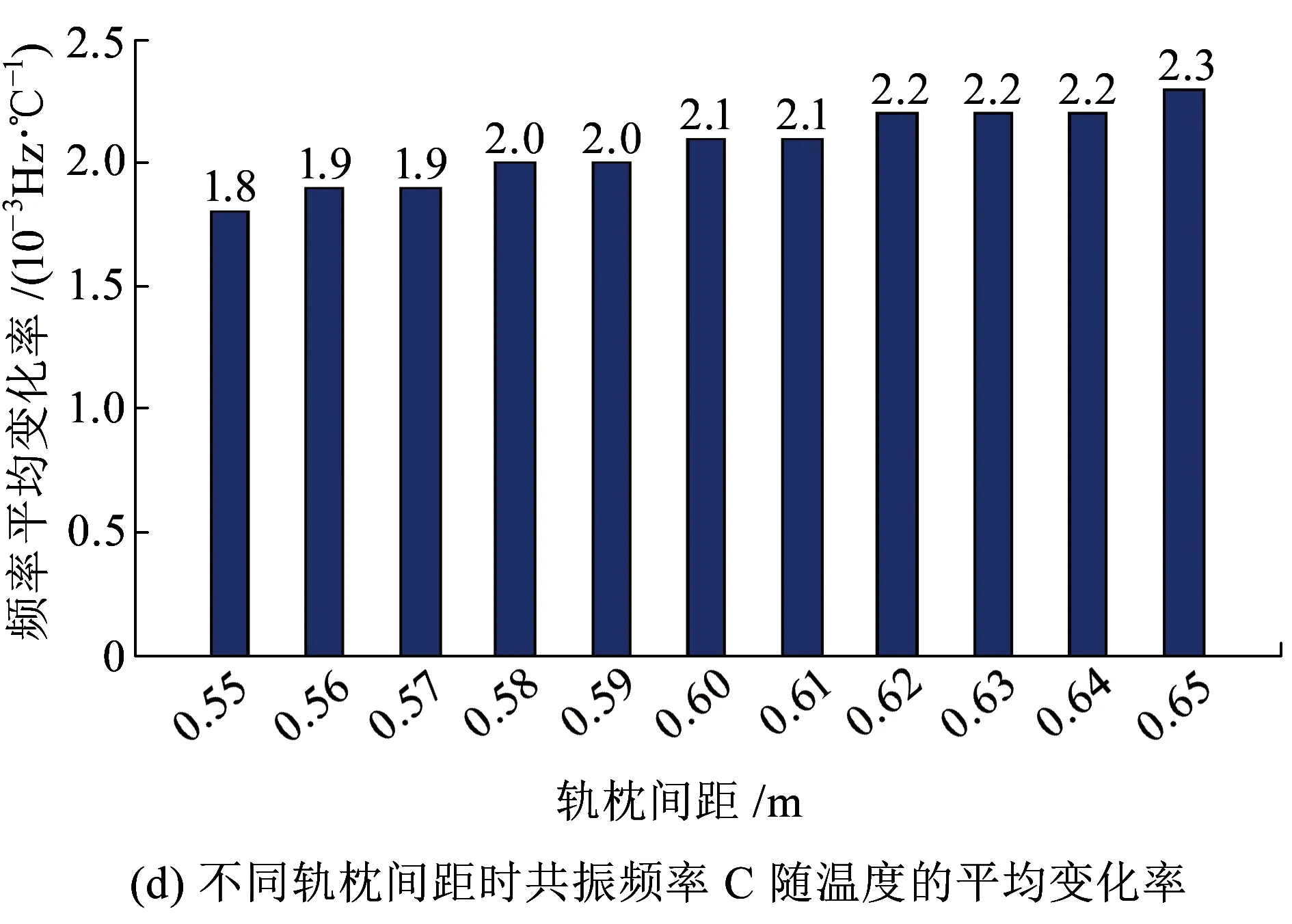
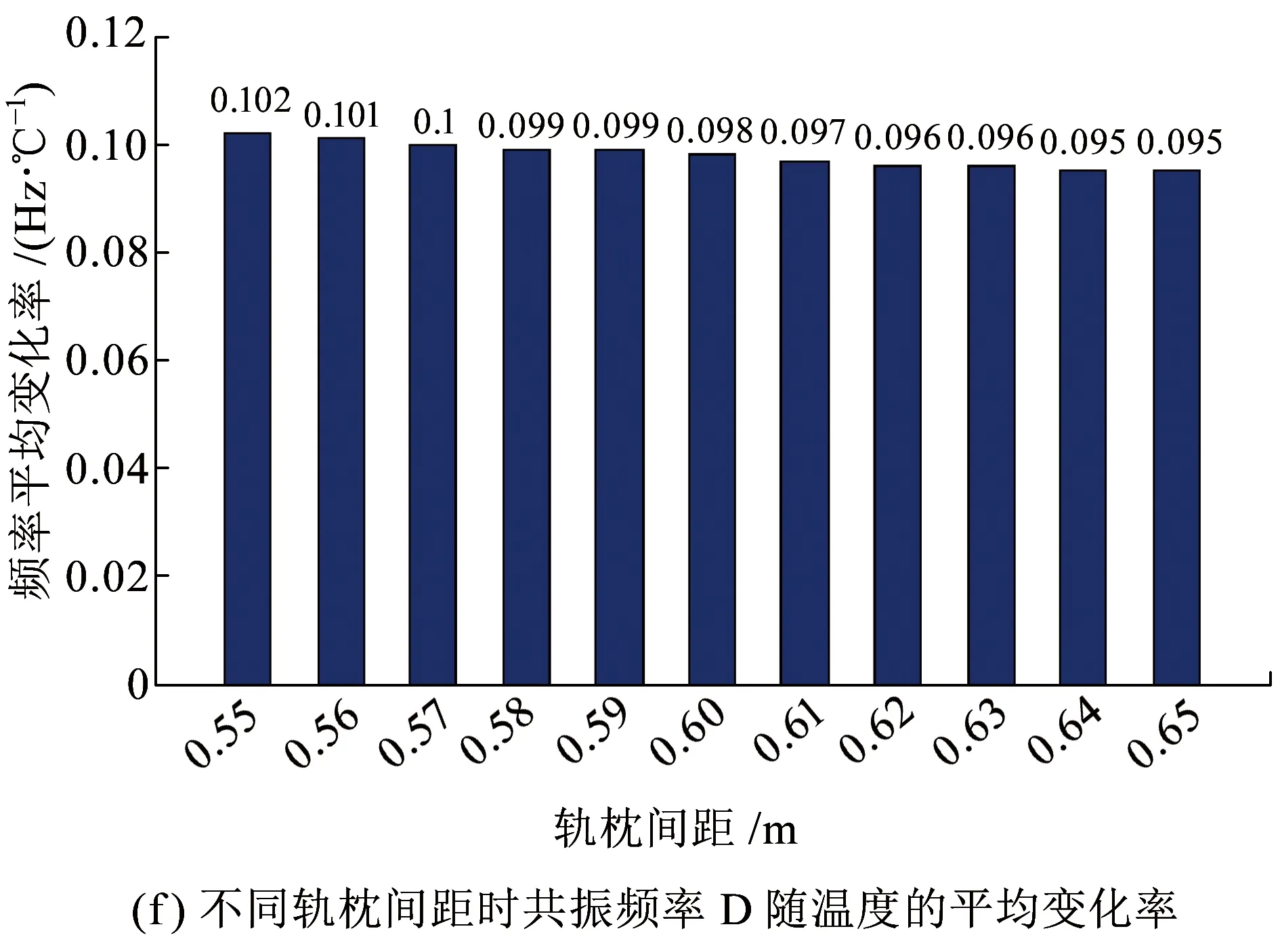
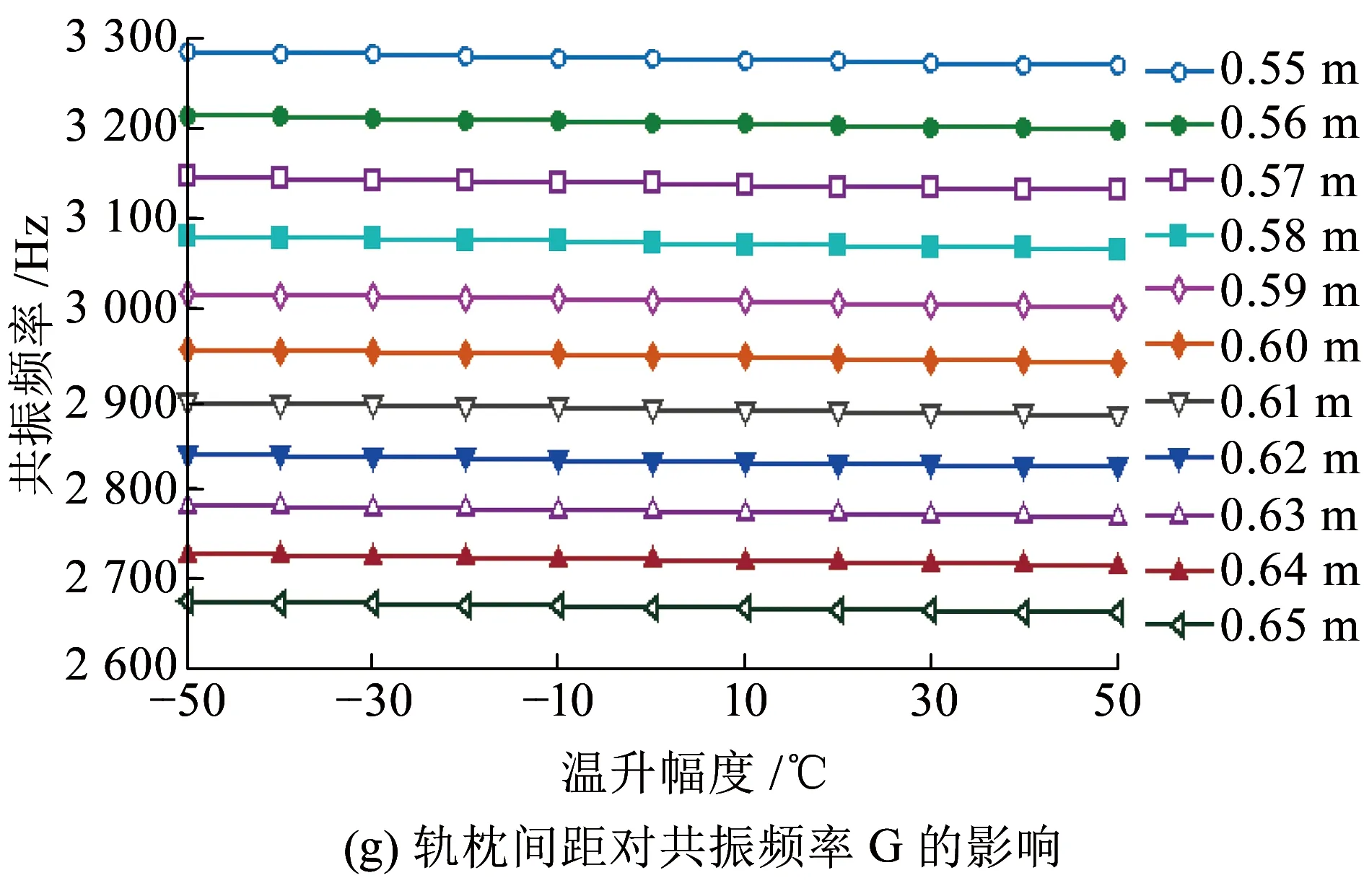
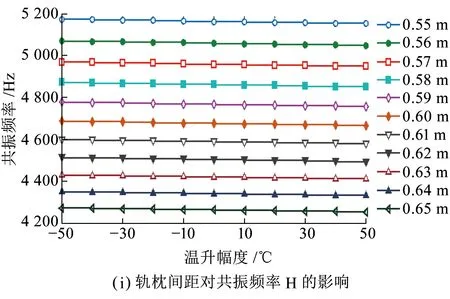
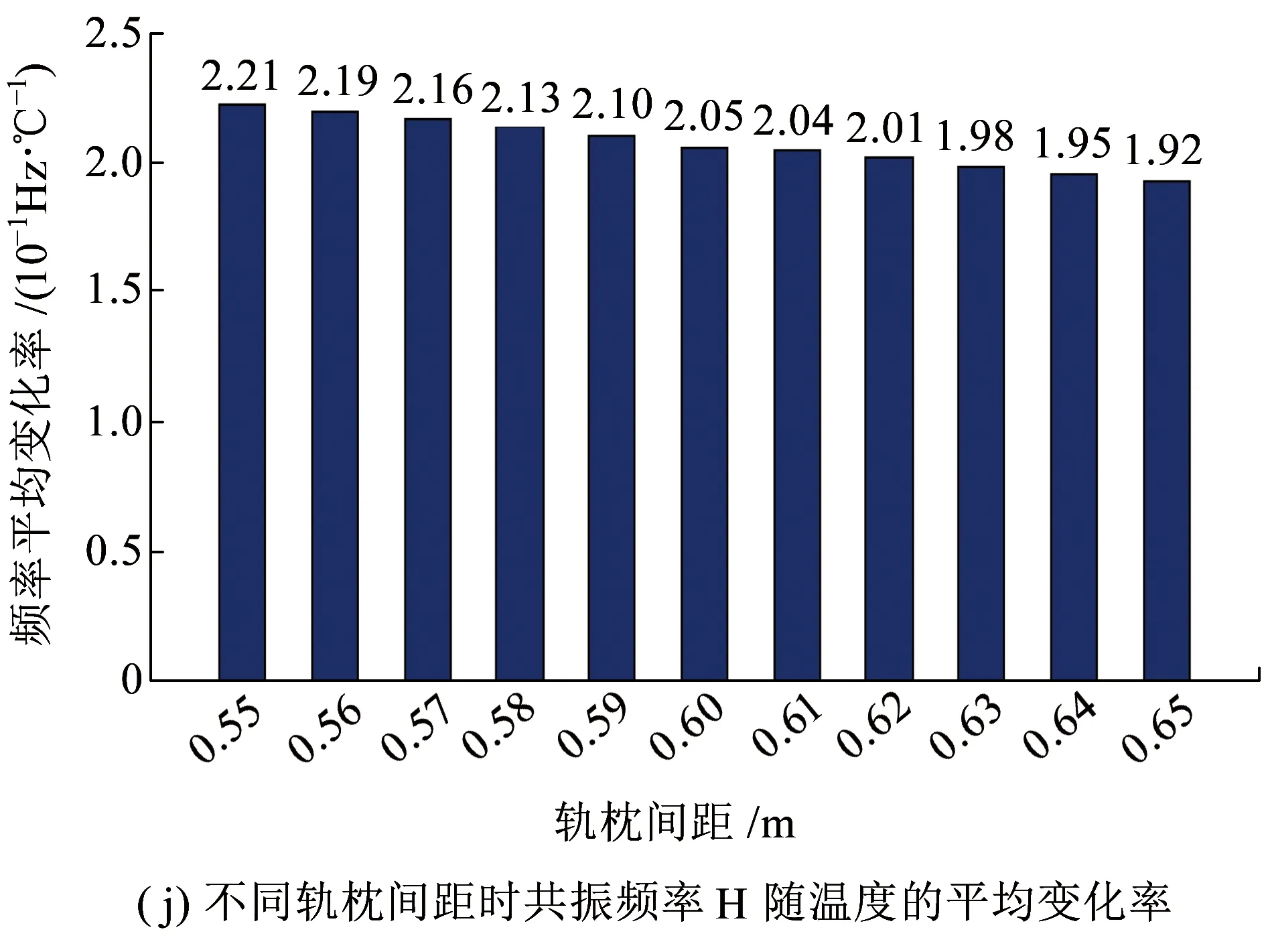
图6 轨枕间距对钢轨共振频率的影响及共振频率随温升的平均变化率

5 结论

本文建立轴向温度力作用下轨道结构周期离散支承梁模型，通过周期结构波数有限元方法分析无轴向温度力作用时周期离散支承钢轨竖向振动的频散特性及位移响应，确定了0～5 000 Hz范围内钢轨的共振频率。通过改变轴向温度力及轨枕间距分析钢轨共振频率的变化规律，得到以下结论：

(1)对于有砟轨道结构，分析其在1 000 Hz以下频带范围的竖向振动特性时，可以采用计算效率较高的连续支承梁模型，分析结果与采用周期离散支承梁模型得到的结果基本一致；对于1 000 Hz以上的频带，采用周期离散支承梁模型较为合适，其可求得轨道结构在高频范围的pinned-pinned共振频率。

(2)对于轴向温度力影响下的周期离散支承轨道结构，钢轨竖向振动各阶共振频率均随轴向温度拉力的增加而增大，随轴向温度压力的增加而减小，且共振频率越大，其受轴向温度力的影响越明显。其中共振频率D、G、H受轴向温度力影响最明显，其平均变化率分别为0.098、0.14、0.205 Hz/℃。因此，可将共振频率D(1 080 Hz)、G(2 947 Hz)、H(4 675 Hz)作为无缝线路钢轨内部温度力大小的主要评价指标。

(3)当轨枕间距发生变化时，钢轨竖向振动各阶共振频率均随轨枕间距的增加而减小，且共振频率越大，其受轨枕间距的影响越明显。在1 000 Hz以下频带内，周期离散支承钢轨的共振频率(A、C)对轴向温度力的敏感性(平均变化率)随轨枕间距的增加而增大；在1 000 Hz以上的频带内，周期离散支承钢轨的共振频率(D、G、H)对轴向温度力的敏感性随轨枕间距的增加而减小。因此，采用振动法分析无缝线路钢轨内部温度力时需先确定轨枕间距。

本文分析中未考虑梁截面变形的影响，根据相关研究[18]，当频率高于3 000 Hz时，横截面变形会对梁的振动特性产生影响，此时钢轨采用实体模型分析更合适。因此，在后续研究中，将结合梁截面变形影响，探讨轴向温度力对周期离散支承钢轨竖向振动特性(3 000 Hz以上)的影响。