一种由粗到精的机载激光测深信号检测方法

王丹菂，徐 青，邢 帅，林雨准，李鹏程

1. 信息工程大学地理空间信息学院，河南 郑州 450052； 2. 近地面探测技术重点实验室，江苏 无锡 214000

机载激光测深(airborne LiDAR bathymetry，ALB)技术可在浅水水域实现快速、密集、精准的测量，已被广泛应用于海洋水深图生产、浅层水域监测、水下目标探测、水下地形三维点云生成等领域[1]。该技术的原理是利用对水体具有较强穿透性的蓝绿激光(532 nm)，通过对蓝绿激光的发射与接收，计算激光在水面、水底的回波时间差，进而反演水深。从ALB系统接收到的波形中检测出水面、水底回波信号的准确位置是测深的首要和关键步骤[2]。但由于水体的动态性，水质的复杂性，水体的漫反射和衰减，系统接收波形中往往存在大量的噪声，且波形形状不固定，给测深信号检测带来困难。

在信号检测中可应用的全波形处理方法大体分为三类：第一类是利用系统接收波形与发射波形间的关系对接收波形进行预处理，包括平均差方函数法[3](average square difference function，ASDF)，维纳滤波去卷积[4](Wiener filter deconvolution，WFD)和理查德森-露西去卷积法[5](Richardson-Lucy deconvolution，RLD)等，该方法能够在一定程度上降低噪声或增强有效信号，提高信号检测的可靠性；第二类是通过设定一个判定指标检测波形中的峰值，从而确定波形中信号的位置，包括极大值检测[3]和一阶导数检测[6]等，这类方法的计算效率高，但如果不对波形进行预处理或对检测结果加以条件约束，容易检测到伪信号；第三类是通过波形分解将波形参数化，获得有关信号的一些属性特征，同时间接确定信号位置，包括高斯分解[7]，三角形函数拟合[8]，四边形函数拟合[9]和指数函数拟合[10]等，这类方法能够得到精确至子采样间隔的信号位置，但需要较为可靠的初值，适合的模型和参数求解算法。上述方法在处理不同类型的波形时都具有一定的局限性：第一类方法只是一种预处理方式，无法实现信号检测；第二类方法只能得到精确至单位采样间隔的结果，且需要设置经验阈值；第三类方法虽然可将结果精确至子采样间隔，但目前针对第三类方法的研究大多只关注于模型的建立， 而对模型参数的求解研究较少。

ALB系统厂商在发布硬件系统的同时也会推出配套的数据处理软件，但其中采用的技术方法并不对用户公开且缺乏通用性：EAARL系统的airborne LiDAR processing system(ALPS)软件为信号检测提供了极大值检测和一阶导数检测方法[11]；文献[12]针对Leica 最新ALB系统HawkEye Ⅲ的配套软件LiDAR survey studio(LSS)展开研究，发现通过简单的均值滤波预处理结合极大值检测可得到与LSS相似的结果；文献[13]也指出Optech的配套软件对波形数据的处理还不够成熟。

基于上述分析，本文提出一种由粗到精的机载激光测深信号检测方法。方法利用波形的有效长度快速估计水深对波形进行分类，将RLD和ASDF算法相结合，以增强对波形的适应性，采用一种包含距离、导数、极值多重约束的逐级检测方法获得可靠的信号位置初值，在此基础上利用改进的二阶多项式指数函数模型拟合波形，并引入信赖域优化算法精确求解模型参数。实测数据和模拟数据证明了方法的有效性和可靠性。

1 研究方法

图1 由粗到精的机载激光测深信号检测方法Fig.1 Flowchart of coarse-to-fine signal detection method for ALB

1.1 接收波形有效长度估计

接收波形有效长度是指测点产生的所有回波信号(有效信号)在波形中占据的总长度。ALB系统为确保能够同时测量陆地和水域，记录的每帧波形都包含上千次采样，而对于每一帧波形，有效信号大约仅占其中的0.8%～5%。因此，确定接收波形的有效范围和有效长度可以大大提高波形的处理效率，为后续处理屏蔽大量噪声。文献[4]认为高于三倍噪声功率且持续时间超过5 ns的回波中存在有效信号。基于此，估计有效长度L的具体步骤为：

(1) 取出接收波形wR的后1%，计算这部分波形的最大值和标准差分别作为截断噪声阈值TN和背景噪声功率σN，选取后1%是因试验数据的总采样长度为6500，即最大测距为780 m，飞行航高为500 m，波形的后1%部分不存在有效信号；

(2) 将wR中各点的强度减去TN，并将结果为负的点置零，以消除大部分背景噪声；

(3) 如图 2所示，对wR从首至尾检索，将第一个存在有效信号的回波首端作为有效范围的首端tmin；再对wR从尾至首检索，将第一个存在有效信号的回波末端作为有效范围的末端tmax，则L=tmax-tmin。其中存在有效信号的判断依据为：波形强度超过3×σN且持续时间大于等于5 ns。

图2 接收波形有效长度估计示意图Fig.2 Illustration of effective length estimation for the received waveform

如图 3所示，水域的蓝绿激光接收波形主要包括3部分：水面反射回波、水底反射回波和水体后向散射。若已知水面与水底回波信号位置tS、tB，则当激光垂直于水面入射，瞬时水深D的计算公式为[14]

式中，c表示光速；n为水体折射率；时间差Δt=tB-tS。对于水域而言，水面、水底反射回波分别为波形的首次和末次回波(图3)，因此将L作为Δt代入式(1)可大致推断出测点的瞬时水深D0。

图3 水域的蓝绿激光接收波形Fig.3 Received waveform of green laser from water

1.2 测深信号粗检测

1.2.1 接收波形预处理

相比于陆域回波信号，测深信号的检测难度更大，其中在两种极端情况下的测深信号最难检测：极浅水域波形的三种主要成分相互交叠，难以区分(图 4(a))；极深水域的水底信号由于水体的衰减作用强度较弱，易与噪声混淆(图 4(b))。因此，需要对波形进行预处理以达到降噪或增强有效信号的目的。虽然平滑滤波可以实现波形的降噪，但同时也会导致有效信号变宽或者峰值位置偏移，有时甚至会滤除掉强度较弱的水底信号。

图4 两种极端情况Fig.4 Two extreme cases

为在不影响有效信号的条件下对波形预处理，文献[15]引入了RLD算法，RLD是一种去卷积算法，原理是将接收波形wR看作是激光发射波形wT与目标横截面p的卷积

wR=p*wT+n

(2)

式中，“*”表示卷积运算，n为附加噪声项。由wR在时间域内迭代反解出p，得到一个逼近极大似然解的结果，它的第i次迭代计算为

文献[3]提出利用ASDF去除波形中的噪声，它的原理是计算不同偏移量t下wR与wT的相关性r

(4)

式中，N为接收波形采样数；τ表示采样间隔。相关性r反映了wR中各采样点处波形与wT的相似程度，由wT卷积生成的有效信号与wT具有较强的相关性，而噪声是随机产生的往往与wT的相关性较弱，因而ASDF可以滤除大部分噪声。ASDF与互相关函数相似，但计算量更小，精度更高。r越小，表明wR与wT的相关性越高，因此ASDF检测的是r的局部极小值。

实际上，没有能够适应所有测深环境下波形的处理方法[17-18]。RLD虽然是一种稳定性较好的去卷积算法，但该算法在波形信噪比较低时可能会增强部分噪声，产生伪信号。ASDF在降噪时会拉伸有效信号，降低信号的分辨率，使一些浅水波形的信号发生交叠。本文结合RLD和ASDF各自的特点，将波形分为浅水、深水两类分开处理。设置一个水深阈值TD，依据测点的瞬时水深近似值D0对波形进行分类。对于水底信号较强但容易与水面信号发生交叠的浅水波形，采用RLD算法提高信号的分辨率；对于水底信号较弱且易与噪声混淆的深水波形，采用ASDF去除与wT相关性较低的噪声。

1.2.2 信号位置初值确定

为提高信号检测的可靠性，文献[3]通过设置最小距离阈值将临近的局部极大值点剔除，但实际作用有限且阈值的适应性差，文献[6]利用波形有效信号附近往往伴有一阶导数极值这一特点，通过查找一阶导数极值来检测有效信号，但仍不可避免受到水体后向散射的影响。本文提出一种逐级检测方法，依次通过距离、一阶导数和极值的约束将检测范围逐步缩小，具体步骤为：

(1) 波形有效信号分别位于p的极大值点或r的极小值点处，为了便于统一处理，对r进行翻转变换

r=max(r)-r

(5)

将p和r统一记为预处理后波形w。

(2) 对w进行极大值检测，将全局极大值点作为水面回波信号位置初值tS0。

(3) 因水底信号位于波形有效范围的末端tmax附近，将检测范围缩小至tmax附近的区域，对这一范围内波形的一阶导数进行极值检测，本文将这一范围设置为[tmax-3×T0，tmax]。

(4) 再将检测范围进一步缩小至一阶导数极值点的邻域内，在检测范围内通过极大值检测确定水底回波信号位置初值tB0。

1.3 测深信号精检测

1.3.1 模型建立

依据波形形状选择合适的模型是波形分解成功的前提。高斯分解虽然能够较好地处理陆域回波波形[19-20]，但高斯函数不能精确拟合水体后向散射，对水域回波处理的适用性有限。文献[7]在不考虑水体后向散射影响的条件下利用两个高斯函数对水深小于2 m的回波波形进行分解。但当水深较深时，水体后向散射将不可被忽略，一些研究提出采用三角形函数[8]，四边形函数[9]和指数函数[10]拟合水体后向散射。基于上述研究和对波形的分析，本文提出一种改进模型：二阶多项式指数函数模型fw(t)

fw(t)=fS(t)+fB(t)+fC(t)

(6)

式中，fS(t)、fB(t)、fC(t)分别为水面回波、水底回波和水体后向散射模型。对水面、水底回波采用高斯模型

式中，(α,μ，σ)为高斯函数的3个参数，分别表示峰值强度，峰值位置和标准差。对于水体后向散射的建模将采用fC1(t)和fC2(t)两种模型，当波形tS0和tB0之间的间隔小于等于4×T0，此时水体后向散射部分的采样点个数较少拟合将产生较大误差且对波形的影响较小可以忽略，因而将此类波形判定为极浅水域，采用高斯模型

当间隔大于4×T0时，采用模型

式中，a、b、c、d分别为水体后向散射四个顶点的横坐标；Ab、Ac为b、c对应的纵坐标，如图 5所示。模型fC2(t)是在现有指数函数模型基础上，将指数函数中的一阶多项式替换为二阶多项式(记为二阶多项式指数函数)。式(9)中a、b、c、d是关于μS、σS、μB、σB的函数，分别取μS-σS，μS+σS，μB-σB，μB+σB；f、g、h是对ln(w(t))在[μS+2×σS，μB-2×σB]部分进行二阶多项式函数线性拟合获得的参数

式中，w(t)为波形分解中处理的波形，由于RLD改变了接收波形各成分的形状，浅水波形将选择原始接收波形，深水波形则选择ASDF处理后的波形。

图5 水体后向散射模型Fig.5 Water column backscatter model

二阶多项式指数函数模型主要从3个方面对现有模型进行了改进：

(1) 将tS0和tB0间隔小于等于4×T0的波形视为极浅水域，参照文献[7]针对极浅水域提出的高斯模型，并在其中加入一个高斯函数用于拟合水体后向散射。

(2) 在对非极浅水域波形处理时，采用二阶多项式指数函数拟合水体后向散射，以提高模型的适用性。

(3) 利用水体后向散射与水面、水底回波的关系，将水体后向散射模型的未知参数定义为水面、水底回波模型未知参数的函数，增加了约束条件，减少了未知参数，增强了模型的稳定性。

1.3.2 模型初始参数及取值范围设定

极浅水域模型参数包括(αS,μS，σS,αB,μB，σB,αC,μC，σC) ，非极浅水域模型参数包括(αS,μS，σS,αB,μB，σB)，其中αS、μS、αB、μB的初值由粗检测结果确定，分别取w(tS0)、tS0、w(tB0)、tB0；σS和σB的初值设定为0.5×T0；αC、μC、σC的初值根据经验分别取0.5×αB、0.5×(μS+μB)、0.5×T0。

为保证参数求解在合理范围内进行，还需要设定模型参数的取值范围，这里将α的范围设置为波形强度的最大、最小值之间，μ的范围设置在初值±50 ns内，σ的范围设置为[0,T0]。

1.3.3 基于信赖域优化算法的模型参数求解

在LiDAR波形分解中，求解模型参数本质上是解一个非线性最小二乘问题。对于波形中n个采样点(xi，yi)，函数模型为f(xi，p)，p为m维模型参数，目标函数可表示为

(11)

为求得式(11)的最优解，可采用高斯牛顿法[7，21]和Levenburg-Marquardt(LM)算法[19，22]。然而传统的高斯牛顿法容易陷入局部最优解，改进的LM算法具有一定的全局收敛性，但在实际应用中依然会受到初值的影响，有时甚至会出现与参数意义相矛盾的结果。为降低对初值的要求，并使参数求解在合理的范围内进行，本文将信赖域优化算法引入模型参数求解。在波形分解中常用的高斯牛顿法，最速下降法和LM算法均属于一维搜索方法。一维搜索方法在每次迭代时通过求导确定搜索方向和步长，从迭代点出发作一维搜索。而信赖域法则是在以迭代点为中心的球域(信赖域)中搜索方向和新的迭代点[23]，从而保证了算法的全局收敛性。

对于目标函数式(11)，设第k次迭代点为p(k)，将Q(p)在p(k)处按泰勒级数展开，并保留至二阶项

(12)

记d=p-p(k)将式(12)转化为二次型

(13)

通过一维搜索方法解得式(14)的最优解d(k)，再判断d(k)的正确性。信赖域法的核心之一在于判断d(k)的正确性，即是否接受这一改进的步长以及如何改变信赖域半径rk。根据所选策略的不同，信赖域法有多种形式[24]，本文仅采用了其中一种，即根据函数值实际下降量与预测下降量之比判断d(k)的正确性[25]

2 试验结果与分析

2.1 试验数据

为验证本文方法的有效性和可靠性，分别选取实测数据和模拟数据开展试验。实测数据是由国产ALB系统“机载双频激光雷达系统”(中科天维公司)在海南某地区获取，具体参数见表1，并挑选了不同深度的3片水域的波形数据进行试验，相关信息见表2。由于海洋是一个处于不断变化的动态环境，其他测量手段又很难与ALB测量保持同步性，因此本文采用人工判读结果作为实测数据真值。人工判读结果虽可靠性较高，但精度无法超越单位采样间隔，为进行更准确的精度分析，本文利用激光测深波形模拟工具Water LiDAR(Wa-LiD)[27]生成0.1-35 m水深下与实测波形形状相似的7000帧模拟波形作为模拟数据，图 6为实测波形与模拟波形的对比，可以看出生成的模拟波形与实测波形的形状是相似的。

表1 实测数据获取参数

表2 实测数据信息

2.2 粗检测试验

该试验采用模拟数据分别将RLD和ASDF算法与逐级检测方法结合检测信号，并与原始波形的处理结果作比较，以检验RLD和ASDF的性能，探究粗检测中阈值TD的设置。由于不同水深下的波形之间存在差异，因此将模拟波形按照深度分为三类：浅水域(水深为0～2 m)，中间水域(水深为2～25 m)，深水域(水深为25～35 m)。定义正确率为水面、水底信号检测误差均小于3×SI的波形帧数占总试验帧数的百分比，用于评定检测结果，3×SI对应为0.36 m的检测误差。

图7为RLD和ASDF分别对浅水波形和深水波形进行预处理的结果，从中可以看出RLD能够对浅水波形中的信号实现较好的增强，ASDF能够在保留测深信号的同时实现去噪。从表3可知，在浅水域的检测中经RLD预处理后的波形检测结果正确率最高，证明RLD能够提高信号的分辨率，分离一部分发生信号重叠的波形，而经ASDF处理后的波形检测率甚至低于原始波形，这是由于ASDF会在一定程度上拉伸信号，使本没有信号重叠的波形发生了重叠，导致信号无法检测；在中间水域的检测中，3种处理方式的正确率均在90%以上，其中，经ASDF处理后的波形检测正确率最高，能够达到99.5%；在深水域的检测中，经预处理后的波形检测的正确率相比原始波形都有较为明显的提高，ASDF的正确率高于RLD，说明虽然RLD能够增强有效信号，但当水底信号强度与噪声相当时，也可能同时增强了噪声，导致检测到了伪信号，而ASDF能够去除与发射信号形状不相似的噪声，在一定程度上避免误检测到噪声。总体来说，RLD更适合处理浅水波形，ASDF更适合处理深水波形，中间水域两种预处理方式皆可。因此在粗检测中用于区别浅水、深水波形的水深阈值TD可设置在中间水域(2～25 m)之间，本文将TD设置为10 m。

表3 粗检测结果的正确率

2.3 水体后向散射建模试验

利用模拟数据生成的水体后向散射波形对4种建模方法进行试验分析，结果见图 8和图 9。图 8为水深10 m时的水体后向散射波形的拟合效果，其中三角形函数的拟合误差为5.0×10-4，四边形函数的拟合误差为1.5×10-4，一阶多项式指数函数的拟合误差为0.5×10-4，二阶多项式指数函数的拟合误差为0.5×10-4。图 9为4种建模方法的拟合误差随水深的变化情况，由于一阶多项式指数函数与二阶多项式指数函数的结果几乎完全相同，因此在图中统一记为指数函数。从试验结果可以看出，指数函数能够适应不同水深下的波形，三角形函数和四边形函数对波形的适应性随深度的增加逐渐降低，两种指数函数在拟合模拟波形时效果差异不大。

图10和图11为实测数据的试验结果，图10左侧为对波形整体拟合的结果，其中一阶多项式指数函数的拟合误差为2.0×10-3，二阶多项式指数函数的拟合误差为1.6×10-3；右侧为水体后向散射部分拟合的结果，横坐标为时间t，纵坐标为波形强度的对数ln(w(t))。图11为两种模型的拟合误差分布，其中二阶多项式指数函数的拟合误差整体上小于一阶多项式指数函数，且误差分布也相对集中，表明二阶多项式指数函数更适合于拟合实测波形。

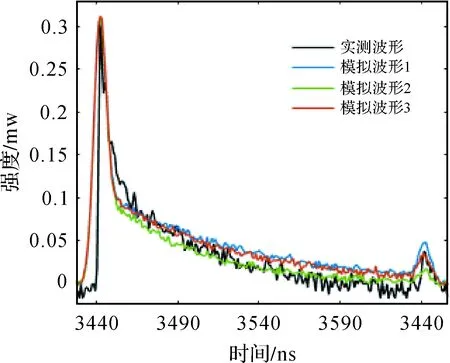
图6 实测波形与模拟波形对比Fig.6 Contrast between field waveform and simulated waveforms

图7 实测波形预处理结果Fig.7 Preprocessing results of field waveforms

图8 模拟波形水体后向散射拟合结果Fig.8 Fitting results of simulated water column backscatter waveforms

2.4 精检测试验

精检测试验分别采用模拟数据、实测数据对本文方法(粗检测、精检测)和5种经典方法(极大值检测法[3](记为MAX)、ASDF法[3]、RLD法[5]、四边形拟合算法[9](记为QUAD)、LM算法[19])进行对比，以验证本文方法对测深信号检测的有效性。试验时为与本文方法形成对照，ASDF法和RLD法的信号检测皆采用本文的逐级检测方法，QUAD法的初值由本文粗检测方法提供，精检测和LM算法基于的是本文提出的粗检测方法和拟合模型。

图9 三种模型的拟合误差对比Fig.9 Comparison of RMSE for three fitting models using simulated waveforms

图10 实测波形拟合结果Fig.10 Fitting results of field waveforms

图11 两种模型的拟合误差对比Fig.11 Comparison of RMSE for two fitting models using field waveforms

表4和图12为模拟数据试验结果。试验统计了误差在3×SI内的正确率，均方根误差(RMSE)以及误差在0.5×SI内的正确率以进一步评定算法的精度。从试验结果可以看出，粗检测相比传统的MAX法，结果的可靠性具有明显的增强；在波形分解中，QUAD法只能够处理较浅水域，随着水深的增加，该算法将不再适用，这也与3.3节的结论相一致；LM和精检测的检测精度最高，但相比之下精检测所采用的信赖域优化算法效果更为突出；精检测中误差小于3×SI的正确率高于粗检测，表明精检测在对波形进行合理建模的过程中，能够在一定程度上修正粗检测提供的初值。

图13为实测数据试验结果。由于实测数据的真值是由人工判读确定的，判读精度大约为一倍SI，因此试验仅对误差小于3×SI的正确率进行统计。实测数据结果总体上与模拟数据相似，但LM的正确率有所降低，这可能是因为实测数据与模拟数据相比波形的形状更不规则，而在对波形形状的适应性上，LM略逊于信赖域法。总的来说，本文方法相比较现有的经典算法在适用性、正确率和精度方面均有明显改进，3×SI的正确率总体提高了5.5%～26.78%，精度提高了20%～40%，特别是对于较难处理的浅水域和深水域波形具有显著优势。

表4 7种检测结果的正确率和误差

图13 不同区域内7种检测结果正确率比较(实测波形)Fig.13 Comparison of seven detection results in different areas using field waveforms

3 结 论

在机载激光测深技术中，不同测深环境下波形的差异性较大，而现有的测深信号检测方法对波形形状的适应性较差，且检测精度受限于系统采样间隔。为此，本文提出了一种由粗到精的机载激光测深信号检测方法。该方法有效融合了RLD和ASDF两种算法的优势，增强了方法对不同波形的适应性；通过对波形整体的合理建模以及利用信赖域优化算法对模型参数的求解，显著提高了测深信号的检测精度。由试验结果得到以下结论:

(1) 在波形预处理中，RLD更适合处理具有较强信噪比但水面、水底信号易发生重叠的浅水波形；ASDF则能够保证在水底信号不被削弱的同时滤除大部分噪声，能够对水底信号强度较弱的深水波形实现较好的去噪。

(2) 改进的二阶多项式指数函数模型对水体后向散射波形的拟合更贴合，对实测波形的拟合相比传统的三角形函数、四边形函数、一阶多项式指数函数模型更精确。

(3) 融合两种预处理方法和逐级检测的粗检测能够顾及不同水深下波形的特点，利用多种约束精确信号检测范围，为精检测提供可靠初值。采用信赖域优化算法求解模型参数的精检测不仅可以将检测位置进一步精确至子采样间隔，而且能够在一定程度上修正粗检测的结果。

虽然本文方法的适应性强、精度高，但同样存在局限性：方法通过检测峰值确定信号位置，但没有考虑到波形的变形可能会导致峰值位置的偏移，此类误差还有待修正；当测深信号的波形被不均匀拉伸时，波形拟合中采用对称分布的高斯函数将不再适合，进一步分析和修正波形变形对测深信号检测的影响是下一步的研究内容。