参数带有区间约束的平差模型迭代算法

谢雪梅，宋迎春，肖兆兵

1. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室，湖南 长沙 410083； 2. 中南大学地球科学与信息物理学院，湖南 长沙 410083； 3. 中南林业科技大学土木工程学院，湖南 长沙 410004

大地测量实际问题中，除了观测信息，还有参数本身或者前期研究中得到一些附加的有用信息或者先验约束信息[1-3]。这些附加信息虽然没有实际观测值的绝对精度或可靠性，但可以降低模型的不适定性，选择合适的解空间，保持参数先验值和验后估值的统计、几何或物理意义，它们在平差模型中的重要体现就是约束条件[4-5]。通过附加约束条件，补充(先验)信息，可以充分利用参数附加信息或先验信息(参数内在的相关性、精度、几何或物理信息)，对部分参数进行约束，可以很好地保证参数解的唯一性和稳定性。有许多的学者，对带有等式或不等式约束的平差模型进行了大量的研究，提出了许多有效的算法[6-11]。然而，在测绘数据处理中，还有一些复杂的先验信息用等式或不等式来表示比较困难，只能用参数的可行区间、噪声范围等来描述[12]。利用区间约束或集合方法来描述复杂先验信息，可以简化平差模型。区间约束平差模型还很少在测量数据处理中应用，仅有少数数学研究学者对它们进行了研究。他们给出的算法非常复杂，强调的是最优解的解算方法[13-18]，并不关心解的精度评估，不适合测量工作中的应用。在测量数据处理中，针对区间约束平差模型，常用的方法是将其转化为不等式约束平差。但这种转换增加了不等式约束的个数，而不等式约束的解算本身就是一件困难的事[8-11]。区间约束是一种简单界约束，又称为框约束或箱形约束[14-17]，在二次规划理论中有大量的研究，如投影梯度方法[14]、分枝定界法[16]、内点算法[18-19]、积极集法[20-21]等。但这些方法非常复杂，不能直接应用于测量数据的处理，需要进行改进和简化。本文将针对区间约束的特点，研究参数带有区间约束的平差模型解算方法，利用矩阵正则分裂方法[22-23]，将平差问题转化成一个简单的二次规划问题，探索一种新的参数估计迭代算法，并针对病态问题，对算法进行验证，证实了将区间约束加入到平差解算中，可以有效提高解的可靠性。本文利用最优估计理论拓展了现有的误差理论与测量平差方法。

1 参变量带有区间约束的平差模型

当参数向量的不确定性用一个区间来描述时，可以建立如下的平差模型

(1)

minF(X)=(L-AX)TP(L-AX)

(2a)

s.t.l≤X≤u

(2b)

由于目标函数F(X)=(L-AX)TP(L-AX)=XT(ATPA)X-2LTPAX+LTPL中，LTPL为一个常量，若设N=ATPA、c=-ATPL，则二次规划问题(2)，可以转化为如下的二次规划问题

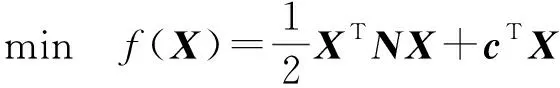
s.t.l≤X≤u

(3b)

已有学者研究了带有不等式约束的平差模型，提出了有效约束的思想[9]。利用这一思想，设L={i:xi=li}、U={i:xi=ui}、E={1,2,…,n}，可以找到E的子集S=L∪U，则区间约束平差模型(3)，等同于具有等式约束的平差模型

式中，BS为对角矩阵，当i∈S时，对角元素bii=1，当i∉S时，对角元素bii=0；dS为向量，当i∈S时，第i分量di=li，或di=ui。由文献[24—25]可知，其参数估计

(6)

此处

σ2(ATPA)-1

因此有

故

由此可知，参数具有线性区间约束的平差模型的参数估计的精度评估可归结为无约束或具有等式约束的平差模型参数估计问题来讨论。寻找有效约束的方法非常复杂，在数据处理中直接利用式(5)来进行参数估计是不可行的,下面介绍一种利用矩阵正则分裂方法，把平差问题转化成一个简单的二次规划问题，建立一种新的参数估计迭代算法。

2 区间不确定性的平差模型的解算方法

这时

(8)

式中

为了求解二次规划问题式(3)，可以先求解

minφ(X)

(9a)

s.t.l≤X≤u

(9b)

Φ(Xk+1+λ(X-Xk+1))-φ(Xk+1)=

Xk+1)+λ(Xk+1-Xk)TM(X-Xk+1)≥0

上式两边除以λ，并令λ→0，可以得到

由上式，顾及(M-H)的正定性，可知，f(Xk+1)

要解决带有区间不确定性平差模型，只要解决二次规划问题式(3)，现设X*是式(3)的最优解，{Xk}是用上面方法得到的二次规划问题式(9)的迭代最优解序列，有f(Xk+1)-f(X*)>0，f(Xk)-f(X*)>0，由于f(Xk)是单调递减，有

即有

f(Xk)-f(X*)=α[f(Xk-1)-f(X*)]=…=

αk[f(X0)-f(X*)]

(10)

这说明limk→∞f(Xk)=f(X*)，即，规划问题(9)得到的迭代最优解序列可以收敛到规划问题(3)的最优解。已有许多文献给出了正则分裂的方法[22-23]。下面是本文给出的一个简单的正则分裂方法：设N的特征值从小到大排列为：λ1、λ2、…、λn，如令M=dI，(M,H)是N的一个正则分裂，即N=H+M，因此，H=N-M，容易计算出M-H=2M-N的特征值为2d-λi，i=1,2,…,n。为了保证M-H的正定性，d只要满足：2d-λn>0，即d>λn/2。

3 区间约束平差模型算法

式中，d为M的对角元素。

由φ(X)可知

4 算例及分析

表1 真实坐标与近似坐标

图1 测边三角网Fig.1 Distance-measuring triangulation network

边号观测边长/m边号观测边长/m15760.70665731.82727804.61175438.40935187.31487493.31947838.89098884.53955483.157107228.509

设τ=[1,1,1,1,1,1,1,1]T，约束区间D1={X:-3τ≤X≤3τ}、D2={X:-6τ≤X≤6τ}、D3={X:-9τ≤X≤9τ},目标函数为F(X)=(L-AX)TP(L-AX),误差平方和的计算公式为

算例1说明，算法收敛的速度与可行域的大小有关，对于系数矩阵列满秩；因为目标函数是凸函数，最优解是唯一的。从表3可以看出针对不同的区间约束，本文算法与最小二乘算法一致，最优解与真值非常接近，说明对于正常的法矩阵。因为观测信息充分，不需要补充先验信息。但是，最优解是在可行域上求得的，当最小二乘解的最优解在可行域(约束区间)D上，由唯一性可知算法得到的解与最小二乘是一致的(先验信息没有起作用)。当最小二乘解的最优解不在可行域D上，说明最小二乘解不符合先验信息，应选择符合先验约束的解。

算例2：修改算例1中已知点P2的坐标为(48 570.013,60 555.845)，让它非常靠近P1点，导致算法1中的系数矩阵病态，用来分析病态问题中算法的性能。此时相应的边长观测也会发生变化，见表4，相应的平差模型的系数矩阵和观测向量为

表3 算法结果及收敛速度比较

表4 边长观测值

5 结束语

大地测量平差模型中的参数通常存在一些不确定的附加信息或先验信息(参数内在的相关性、精度、几何或物理信息)，充分利用它们可以对部分参数进行约束，从而保证参数解的唯一性和稳定性。这些附加信息虽然没有实际观测值的绝对精度或可靠性，但可以降低模型的不适定性，选择合适的解空间，保持参数先验值和验后估值的统计、几何或物理意义，有效提高参数估计的效率。本文针对参数的区间约束信息，提供了一种新的平差方法，其算法简单，可以很好地应用于测量数据处理，提供参数估计的准确率。

表5法矩阵病态时算法的结果比较

Tab.5Algorithmcomparisoninill-posednormalequationmatrix

真 值最小二乘算法本文算法2D1D2D3迭代7302次迭代155028次迭代391691次^X-0.5230-1.3473-0.5105-0.7005-0.8904-2.75806.1625-2.6305-0.63421.36200.902010.44391.08433.20925.3341-0.5360-0.3645-0.5357-0.4968-0.4580-1.56002.8692-1.4581-0.47570.50672.5030-5.90842.30790.4426-1.42282.3340-5.33192.12560.4326-1.2605-2.6650-16.2141-3.0000-6.0000-9.0000F(^X) 0.00431.6861×10-50.00127.4394×10-43.7956×10-4m0504.04410.253730.0253109.4951