一类常微分方程初值问题解的存在与唯一
施 敏
(南京财经大学 应用数学学院,江苏 南京 210023)
在微分方程、积分方程、泛函方程等诸多方程问题的研究中,人们常常会建立与该方程相关的积分算子T,然后将所考虑的方程问题转化为求T的不动点u的问题[1-3],即
u=Tu,
不动点理论是泛函分析的主要组成部分,它有着极其广泛的应用.本文利用Banach压缩映射原理,研究了一类常微分方程初值问题解的存在性与唯一性.下面我们给出本文用到的相关定理及所讨论的微分方程初值问题.
1 预备知识
引理1[4](Banach压缩映射原理) 设X是完备的度量空间,d是X中的距离,设映射T:X→X满足
d(Tx1,Tx2)≤kd(x1,x2),∀x1,x2∈X,
其中0 本文主要讨论下述三阶常微分方程初值问题 (1) 解的存在唯一性问题. 定理1 假设方程(1)满足如下条件: (1) 函数A(x)、B(x)、C(x)在[-r,r]上连续, 并且A(x)、B(x)的原函数分别为a(x)、b(x); 则微分方程初值问题(1)存在唯一的解. 证明 令F(x)=(y,y′,y(2)),则F′(x)=(y′,y(2),y(3)).设 且Γ=(a,b,c),那么方程(1)可转化成如下一阶微分方程: 下面作相应积分算子: T:C([-r,r];R3)→C([-r,r];R3) 使得 因此,初值问题(1)解的存在唯一性问题可以转化为积分算子T是否存在唯一不动点的问题.而对于∀F,G∈C([-r,r];R3),有 因此, 从而, 又由 F-G∞=(f0-g0,f1-g1,f2-g2)∞= 可得 故依据Banach压缩映射原理,算子T是一个压缩映射,具有唯一的不动点,即微分方程初值问题(1)存在唯一的解,从而定理1得证. 虽然微分方程初值问题的求解有很多解析方法,但解析方法只能用来证明解的存在性、唯一性或者求出一些特殊类型的初值问题的解析解.下面我们利用MATLAB软件对与本文相关的微分方程初值问题进行数值仿真. 例在微分方程初值问题(1)中,取A(x)=x,B(x)=x2,C(x)=x2ex,a=1,b=0,c=4,则该微分方程初值问题(1)写为: (2) 则条件(1),(2)成立,依据定理1可知,初值问题(2)存在唯一的解. 利用MATLAB软件编程得到微分方程初值问题(2)的近似解图像(见图1). 图1方程(2)的近似解图像

2 主要结论
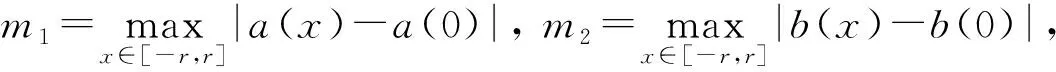




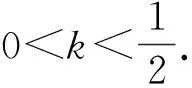

3 数值仿真[5]
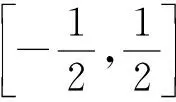
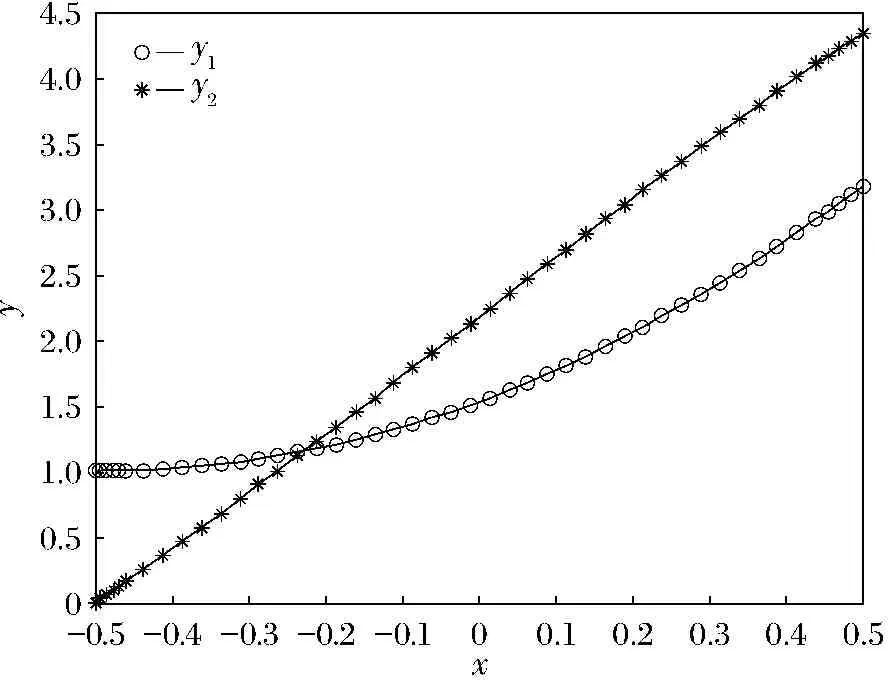
Fig.1 Image of approximate solution of equation(2)

