La2-xSrxCuO4等大温区线性电阻率与带间空穴-声子散射

毛 善 成

(淮阴工学院 图书馆, 江苏 淮安 223003)

传统超导体中库柏对形成的“联胶”是声子. 金属晶体中有自由电子和金属离子, 在费米面附近的两个电子A和B, 当电子A受到来自正离子的吸引力时, 反过来电子A也会吸引正离子, 使正离子偏向自己, 所以A具有一定的正电性, 从而对B电子产生了吸引作用. 这样电子A和B就形成了库柏对, 在低温下发生玻色-爱恩斯坦凝结而产生超导电性. 显然,库柏对的形成要有2个条件, 一是在费米面上,二是晶格振动幅度要特别小, 否则库柏对就会被晶格振动所破坏. 温度低晶格振动幅度才能小, 所以传统超导体的超导转变温度都很低(≤ 40 K). 现在, 高温铜氧化物的超导转变温度可达135 K, 高压下可达164 K, 如此高的超导转变温度是由什么原因引起的呢? 对这个问题的研究国内外已经投入了很多力量, 提出了许多理论模型, 尽管许多理论和概念都很高级, 但在整体的相图面前还是显得软弱无力[1], 有些科学家调侃说,高温超导机理的数量比物理学家的人数还多. 当然,也有一些物理学家给出另一种观点, 高温超导机理虽然还不很清楚, 但一定是在BCS理论框架内[2]. 高温超导材料是通过对铜酸盐进行掺入空穴或电子来获得的超导体, 所以又分为空穴型和电子型2类. 人们通常说的高温超导就是空穴型超导体, 而电子型高温超导体的临界转变温度其实并不高, 只有20 K左右.

超导材料中影响库柏对的形成和稳定的因素主要是晶格振动的幅度,幅度小才能使BCS机制变得显著.降低温度是降低晶格振动幅度的首选方法,其次还有对材料加压、钉轧效应和薄膜化等方法来降低晶格振动的影响.所以传统材料的临界转变温度都比较低,一般不超过40 K,单一金属的临界转变温度不超过10 K.值得注意的是,加压、钉扎、薄膜化等方法可以小幅提高超导临界转变温度(Tc).如果能在高温超导铜氧化物中找到高温条件下晶格的振动幅度被某种因素平衡或吸收,就能对高温超导体的超导临界转变温度为什么如此高给予简单解释.BCS理论的建立是以同位素效应的发现为向导的,于是人们认识到一条辩证规律:电子-声子相互作用是形成电阻的原因,恰好是超导发生的机制[3],也就是符合电阻形成与消失的辩证规律.要搞清楚高温超导机理问题仍然要从空穴型高温超导体正常态的电阻率行为入手.

1 高温超导体正常态的线性电阻率

空穴型高温超导材料中作为结构主体的Cu—O平面内正常态电阻率对温度有线性依赖,其电阻率ρ在很宽的温度范围内有线性的温度关系,如La2-xSrxCuO4的线性关系可从临界超导转变温度Tc附近(～40 K) 延伸到1 100 K,而沿c轴方向电阻率大多数实验结果是半导体型温度行为.高温超导材料Cu—O面正常态电阻率ρab对温度T成线性依赖可用式(1)表示.

ρab=ρ0+βT.

(1)

对不同系列的高温超导材料,此种线性行为非常相似,即对高质量的样品ρ0≈0,比例系数β≈(0.4～0.5)(μΩ·cm)·K-1[4-6].线性电阻率行为本身是一个未解之谜.其次,高温超导材料是一种极性晶体,其氧的电负性比较大,与金属离子La(Ⅲ)、Sr(Ⅱ)等形成离子键,与Cu(Ⅱ)离子之间形成的键比较复杂,是共价键,但有离子键成分.再次,高温超导材料电子的费米速度比较低,约105m·s-1只有传统材料的1/10.所以,在同样的温度下,高温超导材料电子的热动量是传统材料的10倍.在正常态,电子的热动量大,引起晶体振动幅度也大,这是电阻率大的根源,La—Sr—Cu—O正常态电阻率达0.2 mΩ·cm,是Cu在0 ℃电阻率的100多倍.按照BCS理论,电阻率大,电-声作用强,所以有高Tc值,这是高温超导体发现的基本思路.

2 理论模型

超导作为宏观量子力学效应,是一种全局性的行为.如果晶格振动产生的动量能够被电子的热动量所平衡,就可以解释高温超导体的超导转变临界温度为什么如此之高.根据慢电子在极性晶体中的运动规律可以得出电子-声子相互作用状态方程[7].如果系统的总动量为P,m*为电子有效质量,ω为晶格振动频率.根据文献[8],P2/(2m*)=ωћ/(2π),ћ是普朗克常数.电子热动量α(κBTc/vF),κB是玻尔兹曼常数,α=m*/m,m是自由电子质量,vF是费米速度.假设α(κBTc/vF)=P,那么α(κBTc/vF)=[2m*ωћ/(2π)]1/2,所以Tc=vF[2m*ωћ/(2π)]1/2/(ακB)=kvF(ω/α)1/2,k=(2mћ/(2π)]1/2/κB=1.0×10-9为一个常数.如果高温超导体正常态电阻率形成机理为电-声作用,利用量纲分析,则ω=u/ξ,u为声速,ξ为两电子间的声子散射距离,或类似于库柏对的相干长度,所以有

(2)

将式(2)进行变换,得:

(3)

索末菲量子自由电子气的电阻率公式为

ρ=m*vF/(ne2lF).

(4)

式中:n为载流子(空穴)浓度;e为电子电量;lF为电子自由程.将式(3)代入式(4)得高温超导体正常态电阻率计算式

(5)

将各种参数[9]:n=1021·cm-3=1027·m-3,e=1.6×10-19C,u=km·s-1,lF≈ξ≈ξ0=1 nm,α=5,m*=5me=5×9.1×10-31kg,代入β的计算公式,得β=0.4×10-6,和经验值(0.4～0.5)(μΩ·cm)·K-1基本一致.如果电子密度n的取值减小,β的计算值就会增大,有些测量结果偏高,如GdBa2Cu3O7-δ单晶样品在ab平面上电阻一温度关系的测量值[10]β=5.12(μΩ·cm)·K-1.

3 结果与讨论

3.1 线性电阻率与空穴浓度(每个铜氧面的空穴数)

高温超导铜氧化物有多达17个能带,比较重要的有Cu带和O带,掺杂前Cu带上有空穴,掺杂后O上有空穴,掺杂还会引起隙间态的形成,可以说掺入的空穴会按照能带来分布.因此,空穴被限制在一条条能带内.由于高温铜氧化物超导体的基态是电荷转移绝缘体,能带内的电子或空穴由于强的库仑作用使电荷处于局域态.随着掺入空穴浓度的增加,出现多余的空穴进入铜氧面,系统由反铁磁绝缘体向导体转变,形成超导相,可用电子态相图(图1)表示.

高温铜氧化物超导体是掺杂载流子(电子或空穴),并在高温下锻烧而成, 超导发生在Cu—O面上, 与Cu+有关, 也和氧上的电荷转移有关. Cu2+的磁矩为0.5 μB, 表明Cu3d电子不是3d10, 也不是3d9,而是3d9.5. 说明Cu(Ⅱ)和O(-Ⅱ)之间形成了单电子共价键, 这就是掺杂引起的Cu—O面的特殊性所在, 也是铜氧化物能够发生超导的物理化学基础[11]. 根据掺入空穴浓度的多

少,将电子态相图分为极欠掺杂区、欠掺杂区、最佳掺杂区和过掺杂区,分别对应绝缘体、赝隙态、非费米液体和费米液体4种相态.线性电阻率就处于最佳掺杂区.

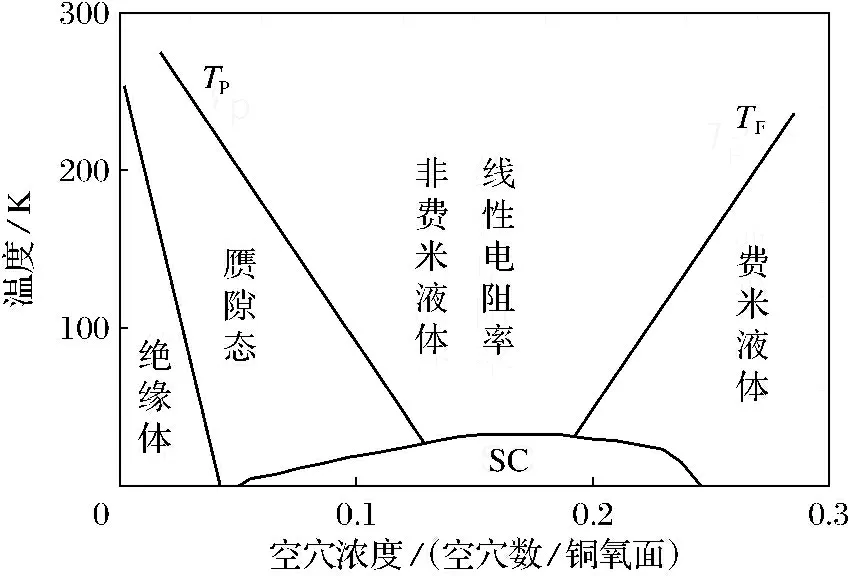
图1 La-Sr-Cu-O的电子态相图
Fig.1 Phase diagram of La-Sr-Cu-O electron states
TP—赝隙温度线;TF—费米液体温度线.

3.2 铜氧面上空穴的费米速度

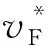
表1 掺杂对高能(电子)费米速度的影响Table 1 The doping dependence of high-energy Fermi velocity in all five materials

3.3 赝隙、能隙与高能电子的费米速度

3.4 铜氧面线性电阻率与两带间的空穴-声子散射

关于铜氧面线性电阻率,文献[16]给出如式(5)的计算,虽然计算结果与经验值一致,但用电-声机制来解释线性电阻率的起因,难以说明大温区(约1 000 K)载流子的自由程为什么不发生变化(缩短)的事实.这里用带间电子-声子散射机制就能给予简单解释.载流子的自由程为两带间的距离,是掺入空穴浓度的函数,与温度无关.用电-声作用来解释线性电阻率遇到到的最大障碍就是载流子自由程随温度升高而下降[17].欠掺杂区高能电子(空穴)的费米速度高,二者的能量差大,所以带间电子-声子散射被抑制,高能带和低能带没有关联,系统表现为赝隙态,没有线性电阻率.最佳掺杂区高能电子的费米速度显著下降,高能带和低能带的能量差为0.211～0.237 eV,几乎为同一平台.能带之间的能量差,又称禁带,一般来说,金属的禁带宽度Eg≤0.2 eV,也就是说,小于 0.2 eV就会出现价带与导带重叠现象.按照上述经验分析,最佳掺杂区两能带能量非常接近,能量差接近0.2 eV,但还不至于重叠,所以能够发生带间电-声散射,表现出非费米液体行为,即线性电阻率.到过掺区,两能带的能量差小于0.2 eV,可能因发生重叠而合二为一,故表现出费米液体行为.超导态服从BCS的理论,正常态的导电行为就会变得与传统金属一样,电阻率与温度的平方成比例.

3.5 中红外吸收峰、拉曼散射与两带间的能量差

高温超导铜酸盐材料的最佳掺杂区有红外光学响应,对应一个很宽的中红外吸收峰为1 800 cm-1,该吸收峰与Tc随掺入空穴浓度变化的走向一致,其谱权重在最佳参杂区,一直以来没有得到很好的解释[18],如果用两带间的能量差来解释就能得到简单而清晰的结果.吸收峰1 800 cm-1对应能量:E=Vcћ=1 800×3×1010×6.62×10-34J=357×10-22J =223×10-3eV=0.223 eV,这个数值正好落在最佳掺杂区,两带间的能量差在0.211～0.237 eV中间.

图2欠掺杂区高能费米速度随空穴浓度变化

Fig.2 The doping dependence of high-energy Fermi velocity in the underdoping ranges

从表1可以看出,两能带间的能量差随掺入空穴浓度的增加而下降,从0掺杂区到过掺区,能量差由近似1 eV逐渐下降到0.15 eV.

高温超导材料的奇特电输运性质源于其能带的不连续性.高温超导机理研究主要有2种观点,一种是电子-电子相互作用,另一种是电子-声子相互作用.电-声相互作用是传统BCS理论的成功见解,然而高温超导体中电-声相互作用与传统金属的电-声作用不同,是带间电子(空穴)-声子相互作用,两带间的距离就是载流子的自由程.能带是不连续的,存在带隙,带隙的大小与掺入的空穴浓度有关,与温度无关.空穴浓度低带隙大,零掺杂时带隙大于1 eV;空穴浓度高带隙小,过掺杂区带隙小于0.2 eV,能带因重叠变为连续,载流子与晶格间库仑相互作用也就大大降低,其电输运性质不再反常.上述研究表明,高温超导机理与线性电阻率的形成机理可能与带间电-声作用有关, 暗示高温超导机理的声子机制仍然不能被排除[20].