求解变系数时滞抛物型方程的高精度数值解法

刘明鼎, 张艳敏

(青岛理工大学 琴岛学院, 山东 青岛 266106)

在刻画物理科学和工程领域中,多数现象的发生过程可以归结为初边值抛物型方程.而时滞抛物型方程更是在刻画传染病的潜伏期、弹性力学的滞后作用、物质和信息的传输等模型方面发挥重要作用.对时滞微分方程解析解的性质和高精度数值解法的研究始终是一个重要的内容,对解析解相关性质的研究多于数值方法的研究[1-12].本文研究了求解一类变系数时滞抛物型方程的一种高精度数值解法.

(1)

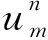
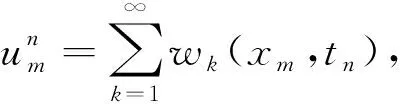
(2)

然后对wk(xm,tn),k=1,2,…,通过递推公式精确求解.用数值算例验证方法的有效性时,只需计算出无穷级数前18项,数值解就能达到比较理想的精度.

1 数值解法格式的构造

将式(1)在点(xm,t)处半离散得到

(3)

在区间[tn,t],t∈(tn,tn+1]上积分得

对式(5)两端进行比较,得出递推公式

(6)

由边值条件,当m=0时,取

(7)

当m=M时,取

(8)

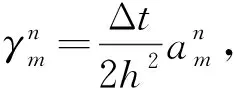
(9)

(10a)

通过式(9)、式(10)计算得到wk(xm,tn+1),k=1,2,…,即有

(11)

2 收敛性证明

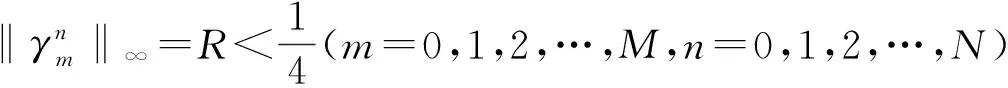
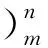
Wk+1=CWk+Fk,k=2,3,…,

(12)

其中,

因无穷级数舍掉有限项不改原变级数敛散性,因此考虑如下级数的收敛性

Wk+1=CWk,k=3,4,….

反复利用上式得到:

Wk+1=Ck-2W3,k=3,4,….

进一步推出

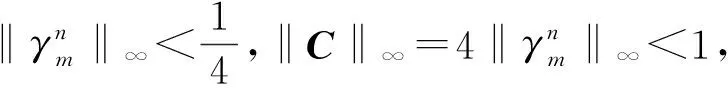
3 稳定性证明

定理2 数值计算方法是无条件稳定.

证明 在等式

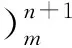
由式(10)、式(11)进一步整理得:

得出对应误差关系式为

将式(16)改写为矩阵方程得:

(17)

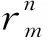
对式(17)整理得:

对式(18)取范数得:

由Kellog定理[7]

‖(I+Cn+1m‖)-1(I-Cnm)‖2≤1,

所以有

不妨设数值解的误差产生于n=0层.即‖εn‖2=0,-p≤n≤-1,当k=1,2,…,p时, 由式(20)计算得:

循环利用式(21)得

显然式(21)对k=0时同样成立,即‖εk‖2≤v0,k=0,1,2,…,p.通过数学归纳法,假设成立不等式

‖εmp+k‖2≤vm,k=0,1,2,…,p,

(23)

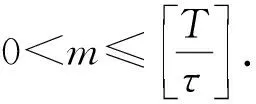
循环利用式(24)得:

(25)

显然不等式(25)对k=0也成立.

则对所有m均成立

‖ε(m+1)p+k‖2≤vm+1,k=0,1,2,…,p.

(26)

又因为

‖εn‖2≤‖εmp+k‖2≤vm=(1+2k1τ)mv0,

(27)

其中,

稳定性证毕.

4 数值算例

算例1

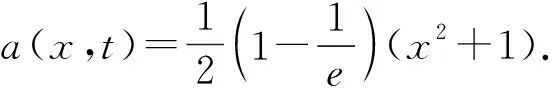
在数值计算时取Δt=0.001,N=1 000,取级数前18项,所得到数值解的相对误差见表1.

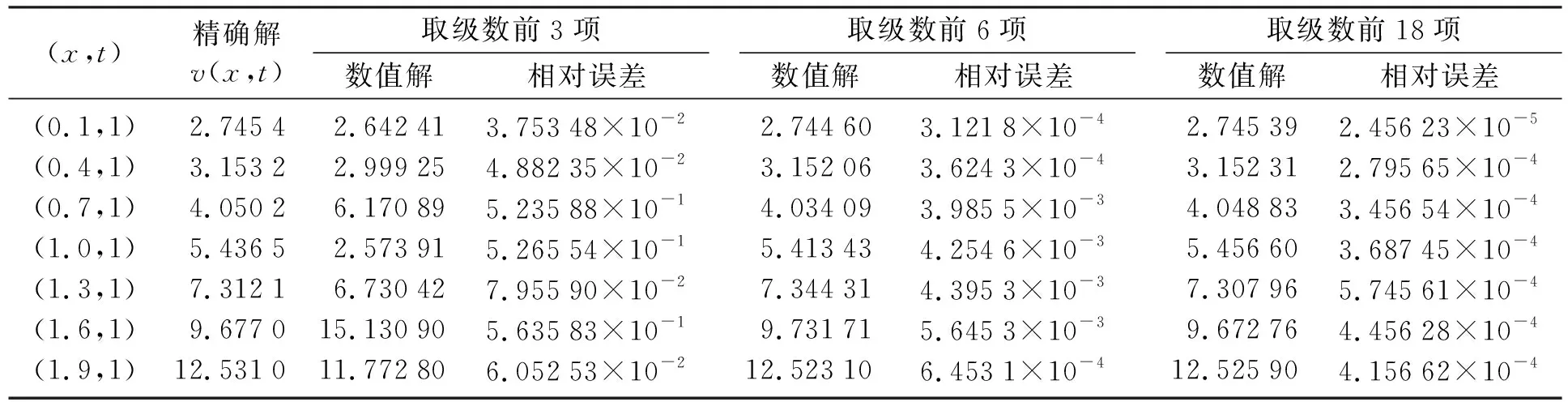
表1 数值解的相对误差Table 1 The relative error of numerical solution

算例2

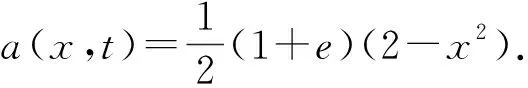
在数值计算时取Δt=0.001,N=1 000,取级数前18项,所得到数值解的相对误差见表2.

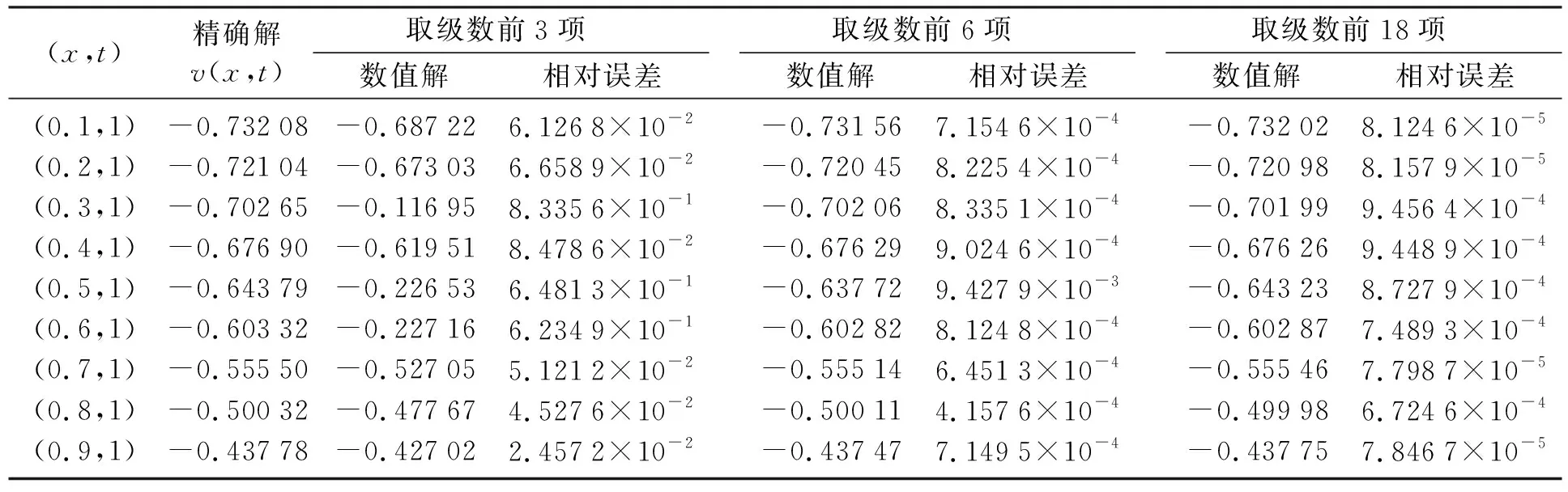
表2 数值解的相对误差Table 2 The relative error of numerical solution

从表1和表2可以看出,在具体计算时取级数(11)的前18项时,就可以达到较好的数值精度.如果取无穷级数项数进一步增加,数值精度会略高于文献[13].从表1与表2的精度对比可以看出,算例2的数值精度比算例1的数值精度略高,因为算例1的精确解沿时间方向为递增函数,算例2的精确解沿时间方向为递减函数.

5 结 语

本文首先对一类时滞抛物型方程利用半离散的方式进行离散,进而得到一种差分格式.再通过将网格节点处的数值解利用无穷级数的形式进行表示后,把无穷级数带入差分方程,结合梯形积分公式,对差分方程进行推导,得到计算无穷级数的递推关系式,可以利用递推关系式算出无穷级数的任意有限项.在通过数值算例验证方法的有效性时,只需要取级数的前18项就可以达到比较好的数值精度.

在后面的工作中,将探讨利用该方法求解分数阶微分方程,进一步检验该方法的有效性.