Ca波段下黑子本影振荡的统计特征∗

何小辉梁莎莎段雅丹梁周渝梁红飞‡

(1云南师范大学物理与电子信息学院昆明650500)

(2云南省高校高能天体物理重点实验室昆明650500)

1 引言

多年来,振荡现象在太阳的各个地区都被广泛地观测到.一个成熟的太阳黑子通常由本影和半影组成:黑暗的中央区域被称为本影,本影周围一圈稍暗的环形区域,称为半影.自从Beckers等[1]首次在Ca II K线中发现本影闪耀,在不同的大气高度发生的太阳黑子振荡现象相继被太阳物理学家观测到.3 yr后(1972年),Bhatnagar等[2]和Beckers等[3]分别在光球和色球中观测到本影振荡.同样在1972年,半影行波也被Giovanelli[4]发现.从此以后,有关太阳的各种波动现象引起了太阳物理学家的广泛关注,并且有新的研究成果不断发现[5−8].早期的观测结果表明:小型黑子本影中整体产生本影振荡,而在较大的本影中有多个振荡源[9].Kobanov等人由Hα和Fe I 6569˚A波段红移和蓝移的强度不同计算出一个太阳黑子中的多普勒速度分布,多普勒速度分布的演化表明:行波以45–60km·s−1的相速度从本影中心向外传播,而且大部分行波传播至本影-半影交界处时会消失[10].Tziotziou等人计算出,一些本影闪耀导致本影波以大约19km·s−1的平均速度向外传播,并且行波以19km·s−1的平均速度跨越本影和半影之间的边界[11].而且Liang等人发现,行波在本影不同位置的波源产生,并在行波的波前以椭圆或圆弧形态向外传播[12].半影行波的发现始于Zirin等人通过在Hα的线心的观测确定了黑子半影内存在周期约为300s、速度约为10km·s−1的强度波[13].而关于半影行波的研究表明:半影行波通常形成于本影的外边缘并在半影内持续传播,在水平方向上传播速度通常在10–20 km·s−1,该速度接近于色球中的声速和光球中的阿尔芬速度,水平方向上的波长通常在2350–3800km,传播方向的张角一般为90◦–180◦,有时甚至可以接近360◦,行波引起活动区内的光强振荡周期约为5 min[14].Yuan等人提出可以利用太阳大气中的振荡功率分布重建其磁和热结构[15];Zhao等人检测到快速移动的波沿着太阳黑子的径向方向从本影移动到太阳黑子边界之外的约15 Mm处.该波的频率范围为2.5–4.0mHz,相速度为45.3km·s−1,远高于光球中阿尔芬波和磁声波的典型速度,它的波阵面以高于当地磁声速的速度传播并扫过光球层[16].

太阳上的振荡现象可能是探测太阳黑子磁场结构、等离子密度、温度等分布特征的重要工具,因此了解活动区振荡现象的性质有非常重要的意义.长期的研究表明:太阳黑子上的振荡主要分为两种,一种是峰值周期约为150s的3 min振荡,另一种是峰值周期约为300s的5 min振荡.而且观测还表明:3 min振荡一般出现在黑子本影内,而5 min振荡一般位于黑子半影中.本影3 min振荡和半影5 min振荡之间是否存在某种联系,一直存在较大分歧:第一种观点认为本影波和半影波之间没有明确的关系,半影行波不是本影振荡的延续,如Christopoulou等人通过对黑子的时间切片图进行傅里叶分析,认为本影振荡和半影行波没有明确的联系[17];第二种观点则认为本影波和半影波具有紧密联系,如Alissandrakis等人检测到产生于本影振荡源并在传播过程中穿过半影的波[18],Tsiropoula等[19]和Alissandrakis等[20]的观测结果提供了波起源于本影内的振荡源,并在传播过程中穿过半影的明确证据,他们认为虽然本影振荡和半影行波是发生在不同位置而且具有不同周期的物理现象,但是它们都是黑子中的波现象,而且一些观测证据也表明一些本影中的波会穿过本影和半影的边界进入半影,因此推测本影振荡和半影行波可能是由同一种行波驱动的,而同一种行波驱动却具有不同周期可能是因为本影和半影中的物理环境比如磁场倾角等因素的区别,造成本影和半影中行波周期和行波引起光强变化周期的对应关系不同.如果行波周期和行波引起的光强变化的周期之间不同的对应关系导致了相同周期的行波产生不同周期的光强变化,那么我们就可以通过确定行波周期和光强周期的对应关系并结合光强的变化周期来确定行波周期,进而比较3 min振荡对应的行波和5 min振荡对应的行波周期是否相同.

2 数据初步处理以及周期的计算

在确定行波周期和光强变化周期对应关系以确定行波真实周期之前,需要先计算光强变化的周期.为了更精确地计算周期,我们需要尽量高的时间分辨率数据.经过筛选,我们选择了2014年3月4日Hinode观测到的一组黑子数据.2014年3月4日,太阳光学望远镜(Solar Optical Telescope简称SOT)观测了位于日面右下角边缘的活动区NOAA11991,并且在约80 min(13:05:31UT—14:24:03UT)的连续观测中获得了2940张清晰的Ca II H的黑子强度图像.其空间分辨率为0.2(′′)/pixel,相邻两张照片拍摄时间间隔为1.6s.这些高时间、高空间分辨率的黑子图像为我们研究黑子振荡现象提供了便利的条件.图1为下载数据后初步处理得到的结果,图1(a)给出了望远镜所拍摄照片的一部分,大小为350pixel×400pixel,拍摄画面为太阳上70′′×80′′即实际太阳表面约为50 Mm×58 Mm大小的区域.图1(b)为对原始数据做相减相后的图像,白色实线为本影和半影的边界,在相减相中我们可以很清楚地看到本影中波的传播.在图中4个白色十字线的位置取样本点以计算振荡周期,白色虚线位置穿过一个振荡源,在白色虚线处做时间切片得到图1(c),在图中可以明显看到黑子本影中的波的传播.

图1 (a):Ca II H线中太阳黑子的样本强度图像.(b):黑子相减相处理后的图像,白色十字标号A–D标记了本影内的采样点的位置.(c):在(b)中白色虚线处的时间切片图像,黑色实线为本影-半影边界,可以在本影内部看到明显的波动现象.Fig.1(a):A sample intensity image of the sunspot in Ca II H line.(b):The sunspot image after adopting the subtraction image processing technique.The white crosses lettered A–D mark the positions of the sample points within the umbra.(c):Take a time slice in the white dotted line of panel(b).The black line is the boundary of the umbra-penumbra.An evident wave phenomenon has been seen in the umbra internal.

在得到的2940张图片中,我们选取连续的且周期性良好的751张数据来研究行波的性质,对A、B、C、D 4个点的光强变化信号使用Jurkevich(JK)方法[21−22]进行分析得到对应样本点的周期图.结果如图2所示,第一行(a)–(d)为在Ca II H波段光强度随时间变化图像,横坐标为时间t;第二行(e)–(h)为使用JK方法分析后得到的周期TW图,纵坐标V2为归一化后的方差.周期图的结果显示每个样本点的周期,样本点A、B、C、D的周期分别为TA=148s、TB=155s、TC=148s、TD=148s.基于样本点的周期我们取其平均值T=149.75s.这个结果表示本影内振荡的平均周期为T=149.75s,是典型的3 min振荡.

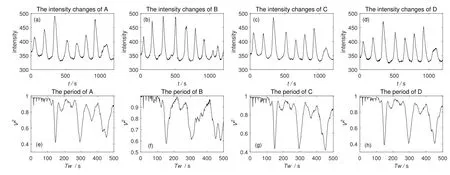
图2 (a)–(d):分别为在样本点A–D处的Ca II H强度变化的时间分布.(e)–(h):JK方法分析得到的相应采样点的周期Fig.2(a)–(d):Time profiles of the Ca II H intensity variation at sample points A–D,respectively.(e)–(h):Period of the corresponding sample points derived from the analysis of JK method

数据经过初步处理,我们得到了本影中亮度的变化周期,大多数情况下我们将本影亮度变化周期看成本影中引起亮度变化的行波的周期.然而,将亮度的变化周期作为引起亮度变化的行波的周期是不严谨的,太阳大气行波很难被直接观测到甚至不可能被观测到,能观测到的只是由行波扰动产生的光强、速度、磁场强度等可观测量,它们有关系但是并不一定是相等的关系.所以为了测定行波的真实周期,需要确定光强变化周期和行波周期的对应关系,以进一步确定行波的周期.

3 本影的统计分析

通常,W和Z之间关系为两种简单的幂函数关系,即W和Z成比例系数为a的正比关系(下文简称正比关系)

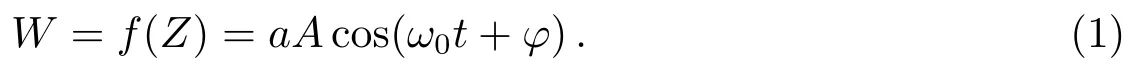
此时W的变化周期与Z的周期相同,如速度、加速度等都属于这种周期变化量.而另外一种为W和Z的平方成比例系数为b的正比关系(下文简称平方正比关系)

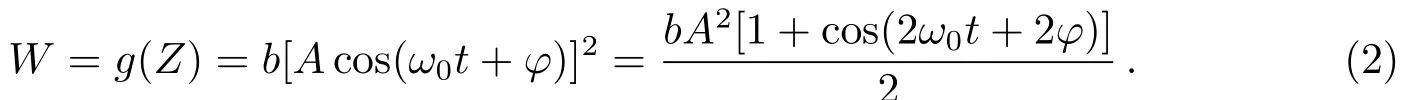
此时W的变化周期即为Z的周期的一半,如动能、势能等都属于这种周期变化量.比较(1)式和(2)式可以看出,如果成正比关系,那么W的峰值便为正数,谷值为负数;如果成平方正比关系,则W的峰值为正且谷值为0.所以理论上可以根据以上差异来区分光强变化周期和行波周期的对应关系.然而实际观测时观测到的并不只有振荡强度,图3所示是本影内某样本点的观测强度变化,观测强度Iobs=Iobs(x,y,t)可表示为以下3部分之和:

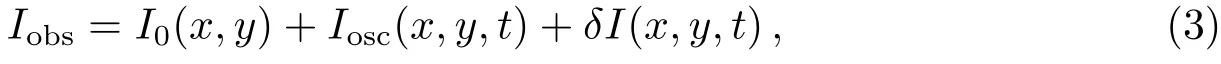
其中I0(x,y)代表样本点M(x,y)的背景辐射强度,并且这是个与时间无关的量;Iosc(x,y,t)代表本影或半影由于振动引起的光强度,它不但是空间位置M(x,y)的函数,也是时间的周期函数;δI(x,y,t)代表观测时的随机噪声.为了方便下面的分析,我们将时间相关项表示为Iv(x,y,t):

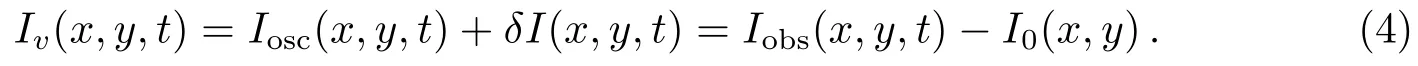
由(3)式可知,我们观测到的光强变化Iobs(x,y,t)并不全是样本点振动引起的光强,而是样本点的背景辐射I0(x,y)、样本点振荡引起的光强Iosc(x,y,t)以及观测时的噪声δI(x,y,t)之和,并且随机噪声远小于振荡强度,背景辐射远大于振荡强度.由于背景辐射的存在,比较样本点W值的正负已不能有效地区分两种对应关系,而且如果样本点的振荡是简谐振动,按照统计规律,在随机噪声影响下无论哪种关系它们的峰值和谷值都会是正态分布.所幸样本点的振荡为非等幅振荡,所以在滤除背景辐射后,对样本点振荡的极值进行统计,如果成正比关系那么峰值和谷值就会成关于0对称的两个偏正态分布;如果成平方正比关系那么谷值就会成一个期望为0的正态分布,而峰值就会成一个偏正态分布.所以,精确研究振荡性质的关键就是确定背景辐射I0(x,y)的值,然后便可得出峰值和谷值的分布规律,根据极值分布情况判断对应关系.这里我们选定光强轮廓线的一个合适的平均值作为稳恒背景辐射I0(x,y)的值.本文尝试选取了两个平均值来代替稳恒背景辐射.

(1)首先想到的就是将样本点强度平均值代替I0(x,y)的值,

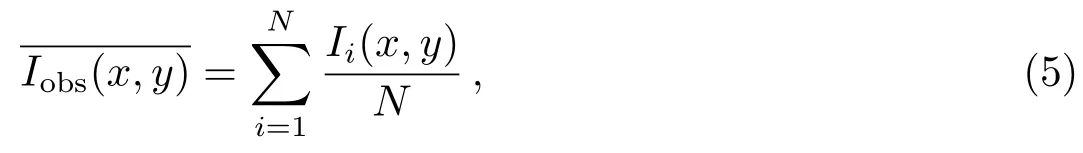
其中,N=751,为统计时所用照片总数,Ii(x,y)为第i张照片中样本点的测量强度.

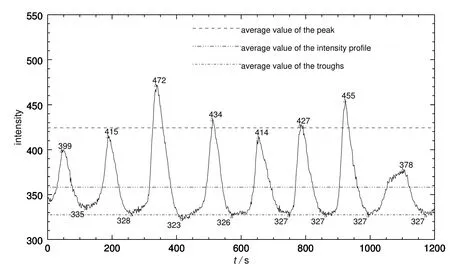
图3 图1中样本点D处的Ca II H强度分布和相应的平均值Fig.3 Ca II H intensity profile at the sample point Din Fig.1 and the corresponding averages

图3所示是图1中样本点D的强度随时间变化图,分别有8个波峰和8个波谷.峰值分别为399、415、472等,相应的平均值=424.25.谷值分别为335、328、323等,与之对应的平均数为=327.5.根据方程(5)我们能算出强度分布的平均值=358.23.在这次统计分析中,我们在本影中挑选了294个样本点并统计了它们的强度分布,在这些分布中获得了2352个峰值和2058个谷值.

将强度平均值当做I0并且从观测强度中减去,则在方程(4)中的时间相关项的和变为我们用分别表示滤除观测平均值后的峰值和谷值,Ip−o,i(x,y)和It−o,i(x,y)的分布如图4所示.在图4中横坐标∆I表示极值和平均值的差值,分别用白色和黑色柱体表示Ip−o,i(x,y)和It−o,i(x,y)的分布.从极值的分布可以看出将平均值看成是背景辐射得到的统计结果没有什么明显的规律,所以将平均值看成背景辐射是不太可能的.排除了将平均值看作背景辐射I0的可能.

图4 将样本点的平均值作为背景辐射时的I t−o(黑)和I p−o(白)分布Fig.4 The distributions ofIt−o(black)and Ip−o(white)when the average value of sample points is considered as the background radiation

(2)从样本点的光强变化曲线我们可以看出它们的谷值基本在一个值上下浮动分布,所以我们的第二种方案为:将强度分布的谷值的平均值代替背景辐射I0.

上式It,i(x,y)表示强度分布的第i个谷值,而Nt表示波谷的个数.

将谷值的平均值看作背景辐射,并从观测光强度中减去.方程(4)中的时间相关项的和变为我们用表示滤除谷值平均值后的峰值和谷值.It−t,i(x,y)分布如图5中所示,It−t,i(x,y)的值集中在区间It−t,i(x,y)∈[−9,10],并且它的分布能用一个正态曲线f(x)=je−(x−ch)2拟合得很好,通过MATLAB拟合得到最佳拟合系数j=168.9、h=0.3368、c=3.278.

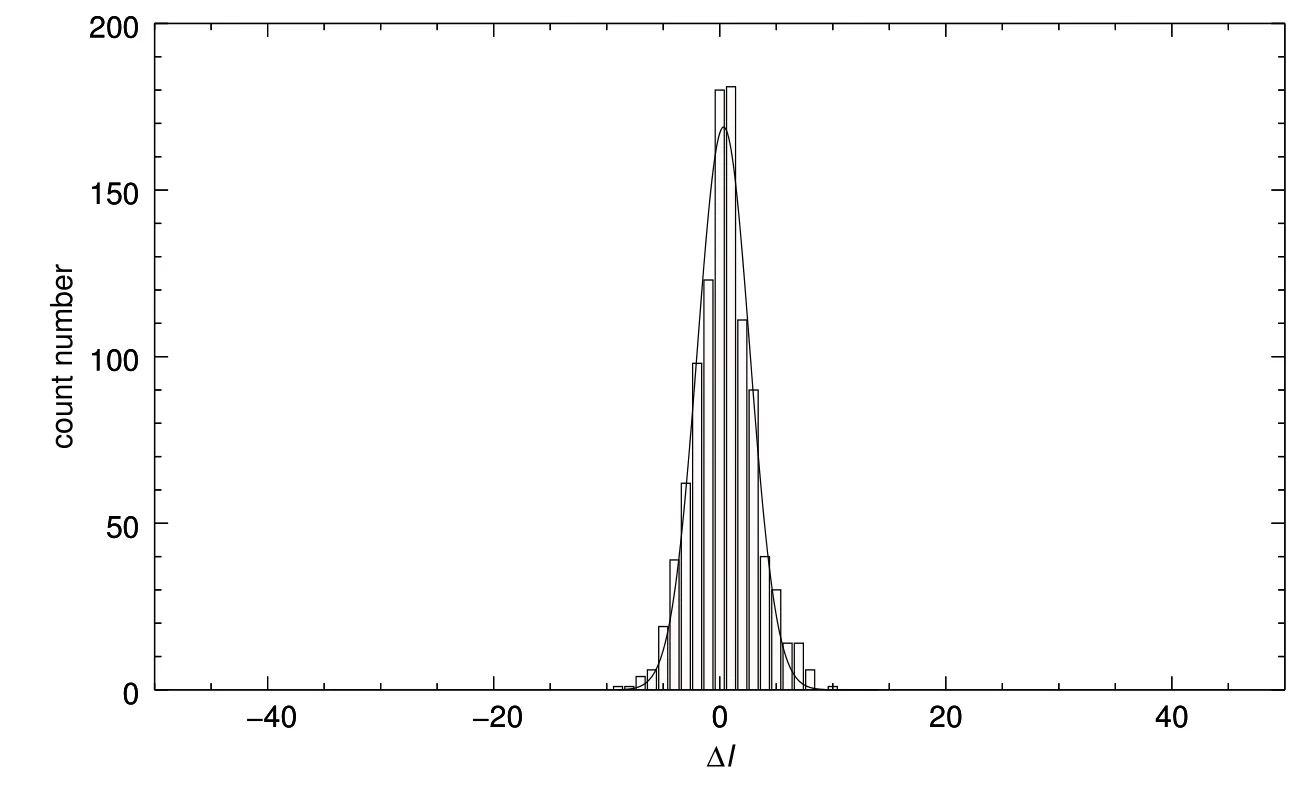
图5 将谷值的平均值作为背景辐射时的I t−t分布,可以拟合成一个正态分布.Fig.5 When the mean value of the valley is used as background radiation,theI t−tdistribution can be fitted as a normal distribution.

Ip−t,i(x,y)分布如图6中所示,我们发现它的分布能拟合成一个偏正态分布曲线:

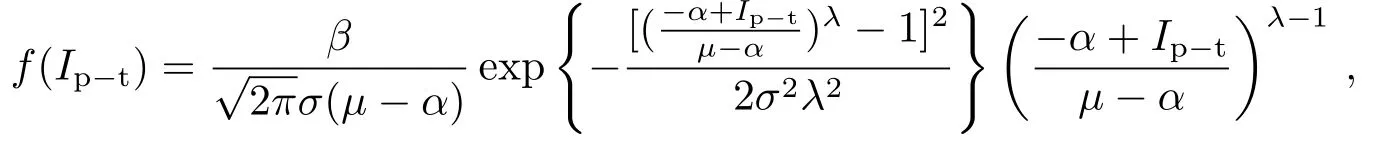
式中α、β、µ、λ以及σ为拟合过程决定的系数,通过拟合Ip−t的分布,我们得到拟合参数α=−0.1,β=2081.1343,σ=0.62043,µ=17.005,λ=0.333577.

图6 将谷值的平均值作为背景辐射时的I p−t分布,可以拟合成一个偏正态分布.Fig.6 When the mean value of the valley is used as background radiation,theIp−tdistribution can be modeled as a partial normal distribution.

经过统计,我们发现将谷值的平均值作为背景辐射I0样本点的极值分布表现出很强的规律性,所以,将样本点强度谷值的平均值作为背景辐射I0是合理的.谷值成一个期望为0的正态分布,峰值成一个偏正态分布,符合之前讨论的成平方正比关系的分布规律,黑子本影中的振荡周期与引起振荡的行波周期可能成平方正比关系.引起振荡的行波真实周期可能为振荡周期的两倍,也就是说行波周期可能为T0=2TW=2×149.75s=299.5s,约为5 min.

4 讨论与结论

黑子本影中的3 min振荡和半影中的5 min振荡的联系一直存在争议,太阳物理学家对此也没有统一的结论.有人认为它们没有关系,有人认为它们有很紧密的联系.本文分析了2014年3月4日Hinode上搭载的SOT拍摄得到的位于日面右下角边缘活动区NOAA11991的一组黑子数据.通过使用JK方法进行分析,获得了本影振荡的周期.为了进一步得到引起本影中振荡的行波的周期,我们需要确定引起本影振荡的行波周期和振荡周期的对应关系.而由于稳恒背景辐射的存在,我们无法直接通过光强的正负来区分引起振荡的行波周期和振荡周期的对应关系,故而选取观测样本点的光强轮廓线的一个合适的平均值当作背景辐射,并将其从光强曲线中滤除.在排除将光强平均值作为背景辐射后,发现在本影中将谷值的平均值作为背景辐射时样本点的极值分布有很强的规律性.

为了研究本影振荡的性质,我们从太阳黑子的本影中选择294个采样点,以分析与采样点的强度分布相关的极值的分布.发现当从观测到的光强度滤除谷值平均值 时,谷值的分布可以拟合成一条关于x=0对称的正态分布曲线,峰值的分布可以拟合成一条偏正态分布曲线.峰值表现为偏正态分布,说明本影振荡不是简谐振荡而是非等幅振荡,谷值表现为正态分布并且期望为0,说明谷值稳定在零上.本影振荡为非等幅振荡,但是谷值却稳定在0上.这说明光强大小可能与振荡位移大小的平方成正比(满足平方正比关系),也就是说光强振荡周期TW可能是引起振荡的行波的真实周期T0的一半.而使用JK方法得到黑子振荡周期约为T=149.75s,再结合统计结果,表明激发本影振荡的行波的主要周期可能是299.5s.即得到行波真实周期可能大约为5 min.以上在Ca II H波段的统计结果和Zhou等人在Hα波段的统计结果[23−24]类似,即本影3 min振荡可能是由周期为5 min的行波驱动的,而半影行波周期也为5 min左右,我们推测本影3 min振荡和半影5 min振荡可能存在某种联系,可能这两种振荡是同一种行波驱动.至于为什么同一种行波在本影中引起3 min的振荡,在半影中却引起5 min的振荡,目前还没有一个自洽的理论.可能是由于本影和半影中的物理环境比如磁场强度、磁场方向、温度等不同导致了它们的对应关系不同,所以在本影和半影中表现出不同的周期.