基于GM(1,1)和M ECM组合模型的GPS卫星钟差中短期预报∗

于 烨张慧君李孝辉肖 波陈婧亚

(1中国科学院国家授时中心西安710600)

(2中国科学院精密导航定位与定时技术重点实验室西安710600)

(3中国科学院大学北京100049)

(4中国科学院大学天文与空间科学学院北京100049)

1 引言

在全球卫星导航定位系统应用中,时间同步是一项关键技术,其精度直接影响导航、定位和授时的精度[1−2].在卫星自主导航中,系统要求地面预报一定时长的卫星星历和钟差作为先验信息,以便导航卫星在没有地面站支撑的条件下,通过一些手段自主完成轨道的确定和广播星历的播发[3−4].但是,由于星载原子钟极易受到外界和自身因素的影响而很难掌握其复杂细致的变化规律.因此,建立精确的原子钟运行模型变得非常困难,相应地准确预报卫星钟差也非常困难.

目前,国内外许多学者在卫星钟差预报方面开展了广泛深入的研究,提出的卫星钟差预报模型主要有:二次多项式模型(Quadratic Polynomial Model,QPM)、灰色预报模型(Grey Model,GM(1,1))、最小二乘支持向量机(Least Squares Support Vector Machines,LS-SVM)、自回归滑动平均(Auto-Regressive Moving Average,ARMA)模型、人工神经网络(Artificial Neural Network,ANN)模型、卡尔曼滤波(Kalman Filter,KF)模型等[5−10].这些预报方法分别适用于不同条件下导航卫星原子钟钟差的短期、中期和长期预报,但也均有各自的适用范围和局限性.

本文针对卫星钟差呈现趋势项和随机项变化的特点,提出基于GM(1,1)和MECM的组合预报模型.该模型首先采用GM(1,1)预报钟差的趋势项部分,然后利用MECM模型对GM(1,1)残差序列进行建模后预报,最后将GM(1,1)和MECM模型的预报结果对应相加得到钟差的最终预报值.此外,采用IGS公布的事后精密卫星钟差产品进行预报试验,通过与卫星钟差预报中常用的二次多项式模型和使用MECM模型预报结果的对比分析,验证了该方法的优越性和有效性.

2 组合预报模型

2.1 GM(1,1)预报模型

在灰色系统理论中,GM(1,1)预报模型是最常用的一种灰色系统模型,它是由一个仅包含单变量的1阶微分方程所构成的预报模型,适合对自身数据的预报,而且具有只需要少量的数据建模的优点[11].设有序列为X(0)={x(0)(1),x(0)(2),···,x(0)(n)},通过一次累加生成新的数据序列X(1):

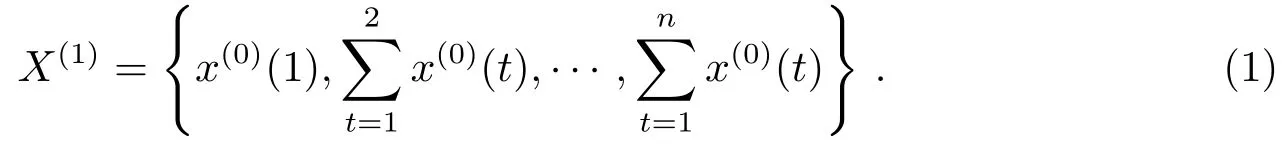
对累加序列X(1)建立1阶微分方程:

其中,参数a为发展系数,参数u为灰作用量.对(2)式进行离散化处理,可得矩阵方程:

其中

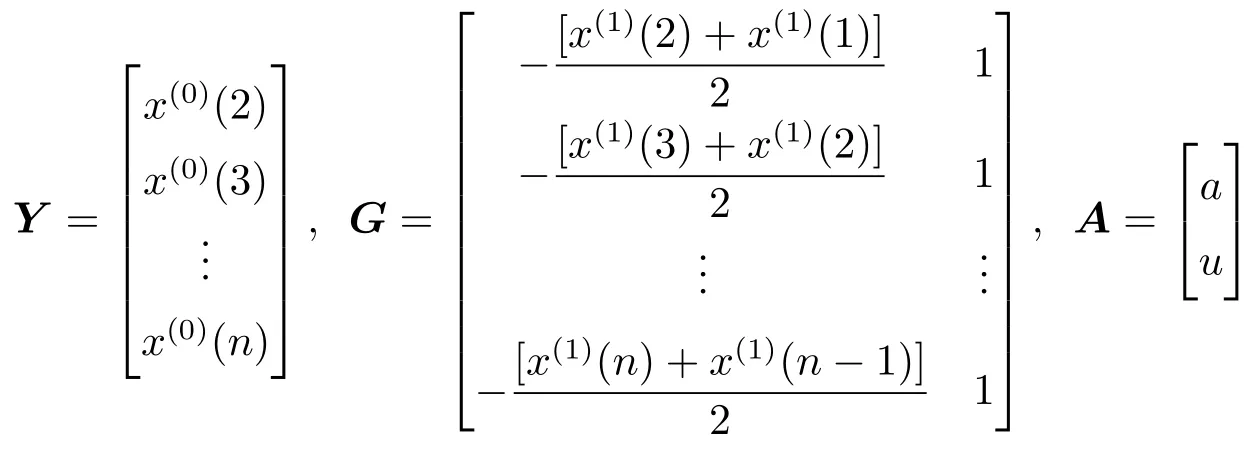
根据最小二乘法可得矩阵方程(3)的最小二乘解为:

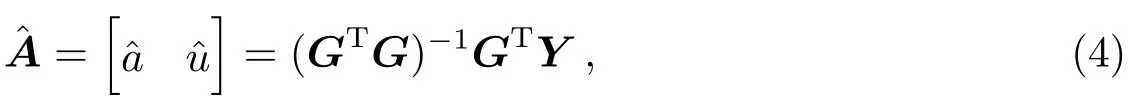
求解时间响应函数(5)式的解为:

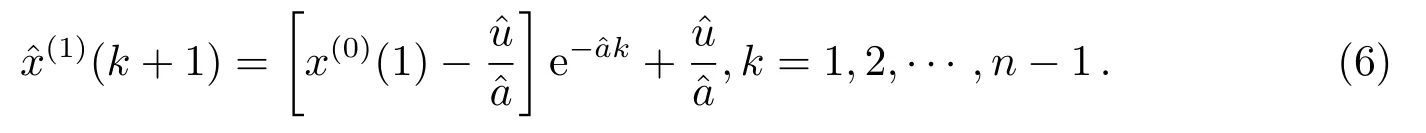
由于序列X(1)是序列X(0)的累加序列,所以原始序列X(0)的预报模型为:

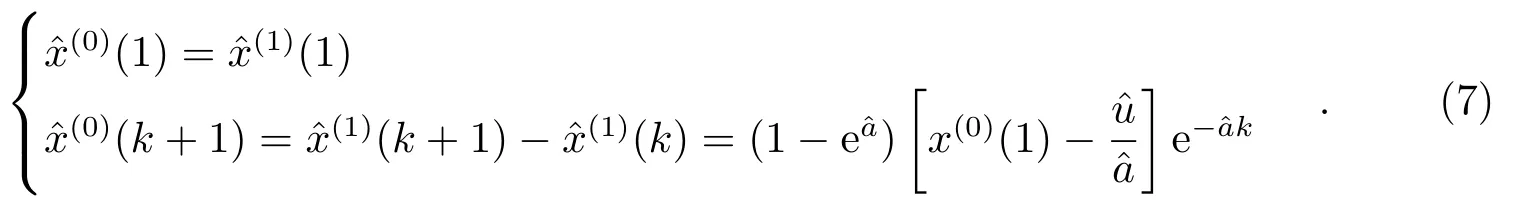
其中,k为参与预报的原始序列数据的个数.原始序列的一般形式为:

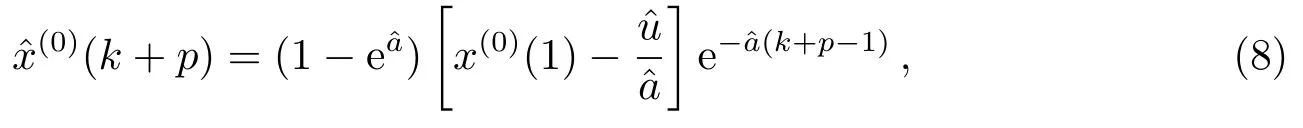
其中,p为预报点数.由以上预报模型即可对未来任意时刻的数据序列进行预报.

2.2 MECM预报模型

修正指数曲线法预报模型描述的是数据序列在一段时间内按指数曲线增长,随着时间的推移,增长趋势会减缓[12].设观测序列为:y1,y2,y3,···,yn,所对应的时刻为:t1,t2,t3,···,tn.可以建立修正指数曲线模型如下:

其中,这3个参数K、d、b均需要用历史数据来确定.这里当K值可预先确定时,采用最小二乘法确定模型中的参数.而当K值不能预先确定时,可采用三和法来估计参数K、d、b.

把n个观测数据三等分,每个部分有m个,且n=3m.具体划分如下:

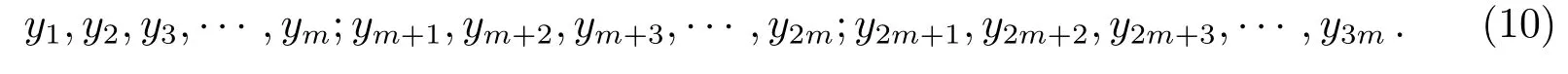
令每部分的趋势值之和等于相应的观测值之和.三和法参数估计的基本步骤可归结为如下过程:

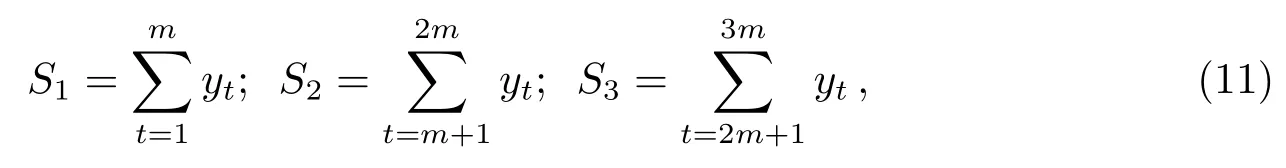
其中,Si(i=1,2,3)表示数据观测值的各部分之和,且

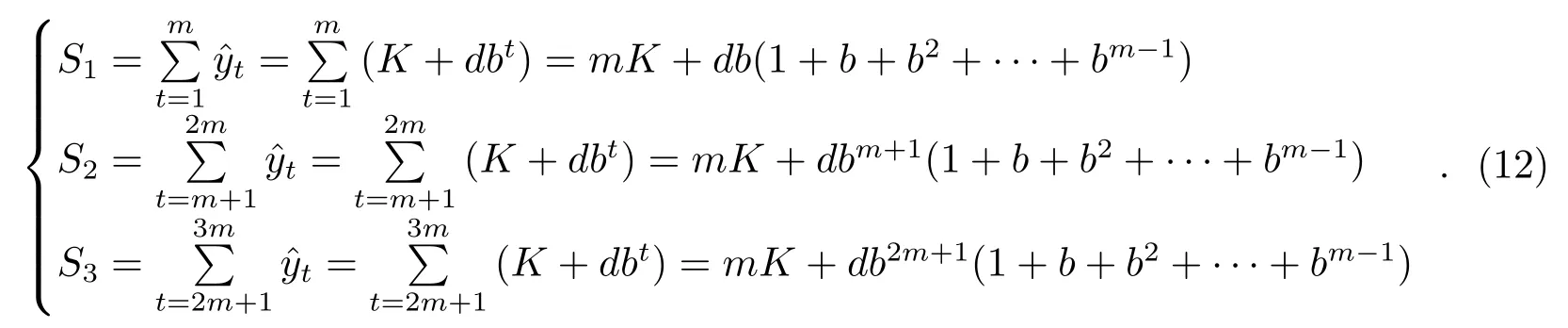
因为

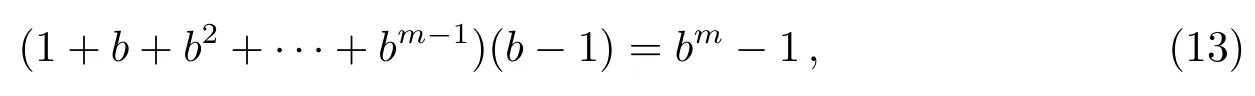
所以,

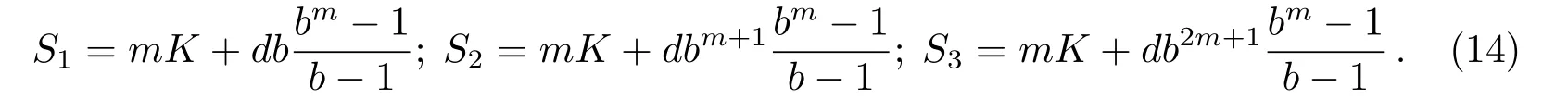
由(12)–(14)式可得:

利用该模型即可对未来任意时刻的数据序列进行预报.

2.3 预报过程

卫星钟差数据序列可以认为是由趋势项和随机项两部分叠加而成,针对它的这一特点,提出一种基于GM(1,1)和MECM的组合预报模型.运用此组合模型去预报卫星钟差的预报流程如图1所示,具体步骤如下所述:

(1)卫星钟差观测数据预处理.首先剔除卫星钟差观测序列中的异常钟差数据,然后采用拉格朗日插值法把缺失的钟差数据补齐.

(2)利用GM(1,1)预报模型提取卫星钟差序列的趋势项部分,并对其进行外推预报.

(3)利用MECM预报模型对GM(1,1)模型的建模残差,即卫星钟差中的随机项部分进行建模并外推预报.

(4)将利用GM(1,1)模型预报的趋势项序列和利用MECM模型预报的对应随机项序列相加,即得到卫星钟差序列最终的预报值.

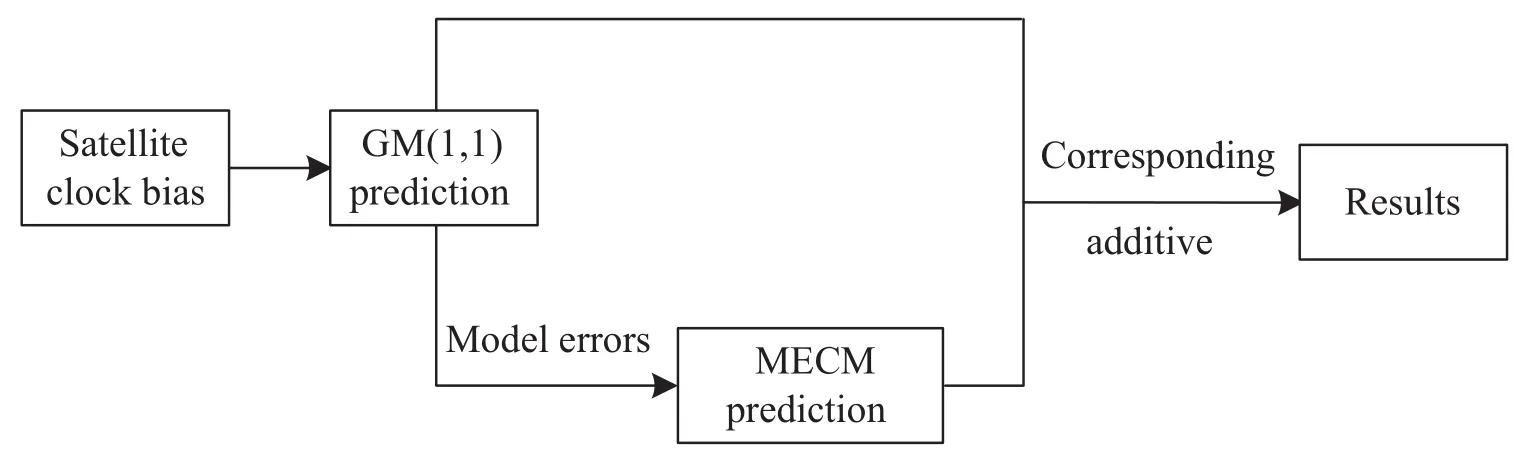
图1 基于GM(1,1)和MECM组合模型的卫星钟差预报流程Fig.1 Satellite clock bias prediction processing based on a combined model of GM(1,1)and MECM combination model

3 算例与分析

3.1 数据来源

为了验证该组合模型的有效性,从IGS服务器(ftp://cddis.gsfc.nasa.gov)上下载了2017年3月5日至6日共两天的IGS事后精密钟差产品进行预报试验,其采样间隔为15min.考虑到目前在轨的GPS卫星有30多颗且我国北斗二代系统搭载的是铷原子钟,所以我们选3颗装载铷原子钟的卫星进行预报试验.本算例随机选取了1颗GPS Block IIF-M型卫星PRN17、1颗GPSBlock IIF型卫星PRN03和1颗GPSBlock IIR型卫星PRN16的钟差数据进行预报试验.

3.2 建模方案

3.2.1 方案一:用12h的钟差数据建模后预报

选用二次多项式模型(QPM)、修正指数曲线法预报模型(MECM)、基于GM(1,1)和MECM的组合模型(GM(1,1)+MECM),用12h的钟差数据建模,分别对未来6h、12h、18h和24h的卫星钟差进行中短期预报.

3.2.2 方案二:用24h的钟差数据建模后预报

选用二次多项式模型(QPM)、修正指数曲线法预报模型(MECM)、基于GM(1,1)和MECM的组合模型(GM(1,1)+MECM),用24h的钟差数据建模,分别对未来6h、12h、18h和24h的卫星钟差进行中短期预报.

3.3 预报结果与分析

使用方案一和方案二对PRN17号(IIR-M-Rb)、PRN03号(IIF-Rb)和PRN16号(IIRRb)卫星钟差进行建模后预报.将接下来6h、12h、18h和24h的实际观测钟差数据与各模型的预报钟差数据相减就得到了预报误差,取各模型预报误差序列的均方根误差(RMS)(具体计算公式见(17)式所示)为衡量预报精度的标准,结果如图2–8和表1所示,其中图2、图4和图6分别为用12h钟差数据建立二次多项式模型、修正指数曲线法预报模型和基于GM(1,1)和MECM的组合模型去预报未来6h(a)、12h(b)、18h(c)和24h(d)钟差数据的预报误差变化图,图3、图5和图7分别为用24h钟差数据建立二次多项式模型、修正指数曲线法预报模型和基于GM(1,1)和MECM的组合模型预报未来6h(a)、12h(b)、18h(c)和24h(d)钟差数据的预报误差变化图.图8为方案一(a)和方案二(b)各模型预报卫星钟差的平均预报精度的对比图.

由于本试验使用的是IGS服务器上公布的事后精密钟差产品,其自身的误差小于0.1ns,故可以作为“真值”,使用RMS作为统计量,去检验二次多项式模型、修正指数曲线法预报模型和基于GM(1,1)与MECM的组合模型所预报结果的好坏程度,计算公式如下:

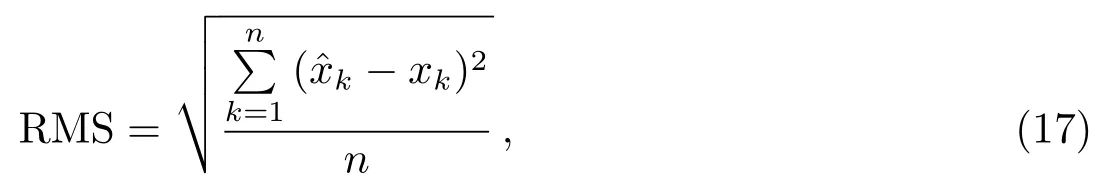
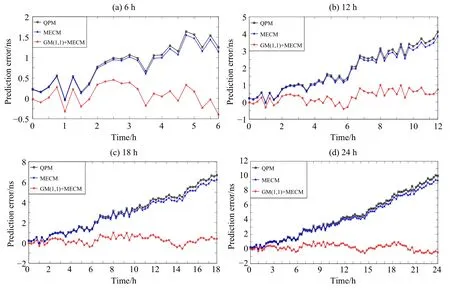
图2 PRN17用12 h数据建模预报6 h(a)、12 h(b)、18 h(c)和24 h(d)的预报误差Fig.2 PRN17 prediction errors of 6 h(a),12 h(b),18 h(c),and 24 h(d)by using 12 h data modeling

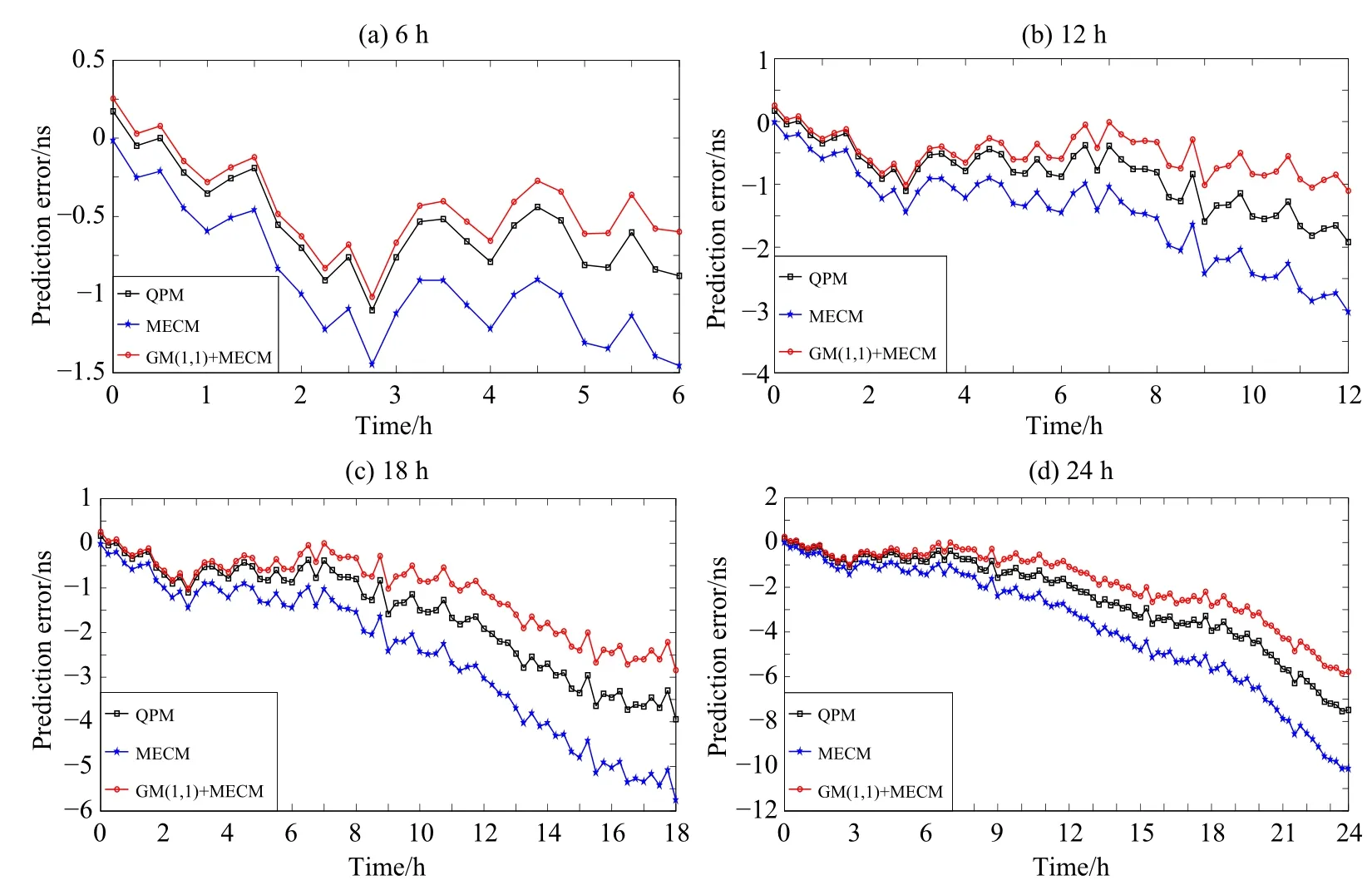
图3 PRN17用24 h数据建模预报6 h(a)、12 h(b)、18 h(c)和24 h(d)的预报误差Fig.3 PRN17 prediction errors of 6 h(a),12 h(b),18 h(c),and 24 h(d)by using 24 h data modeling

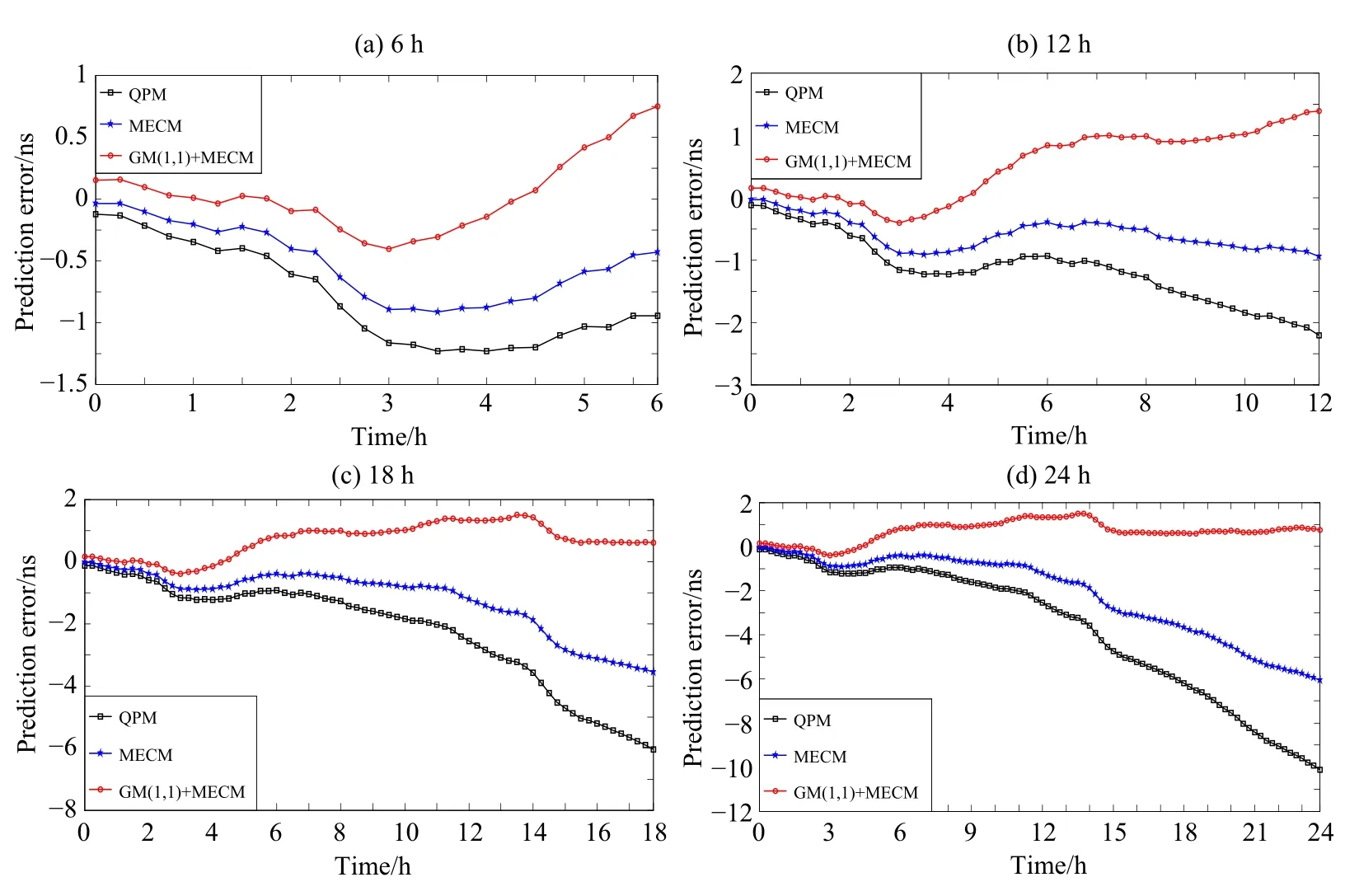
图4 PRN03用12 h数据建模预报6 h(a)、12 h(b)、18 h(c)和24 h(d)的预报误差Fig.4 PRN03 prediction errors of 6 h(a),12 h(b),18 h(c),and 24 h(d)by using 12 h data modeling

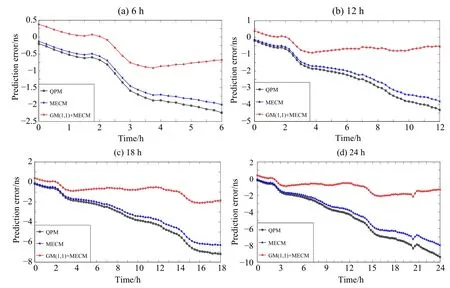
图5 PRN03用24 h数据建模预报6 h(a)、12 h(b)、18 h(c)和24 h(d)的预报误差Fig.5 PRN03 prediction errors of 6 h(a),12 h(b),18 h(c),and 24 h(d)by using 24 h data modeling

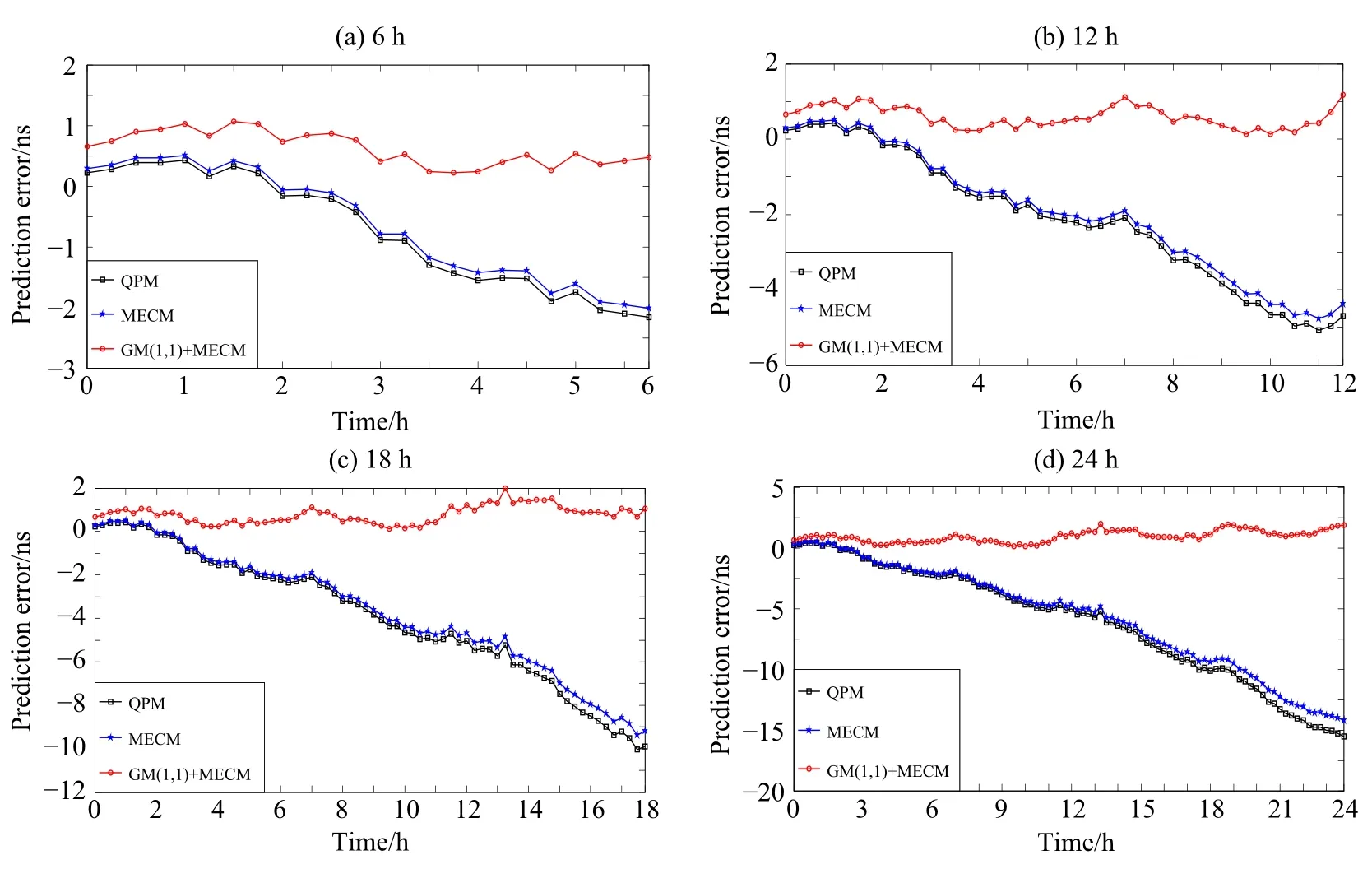
图6 PRN16用12 h数据建模预报6 h(a)、12 h(b)、18 h(c)和24 h(d)的预报误差Fig.6 PRN16 prediction errors of 6 h(a),12 h(b),18 h(c),and 24 h(d)by using 12 h data modeling

图7 PRN16用24 h数据建模预报6 h(a)、12 h(b)、18 h(c)和24 h(d)的预报误差Fig.7 PRN16 prediction errors of 6 h(a),12 h(b),18 h(c),and 24 h(d)by using 24 h data modeling

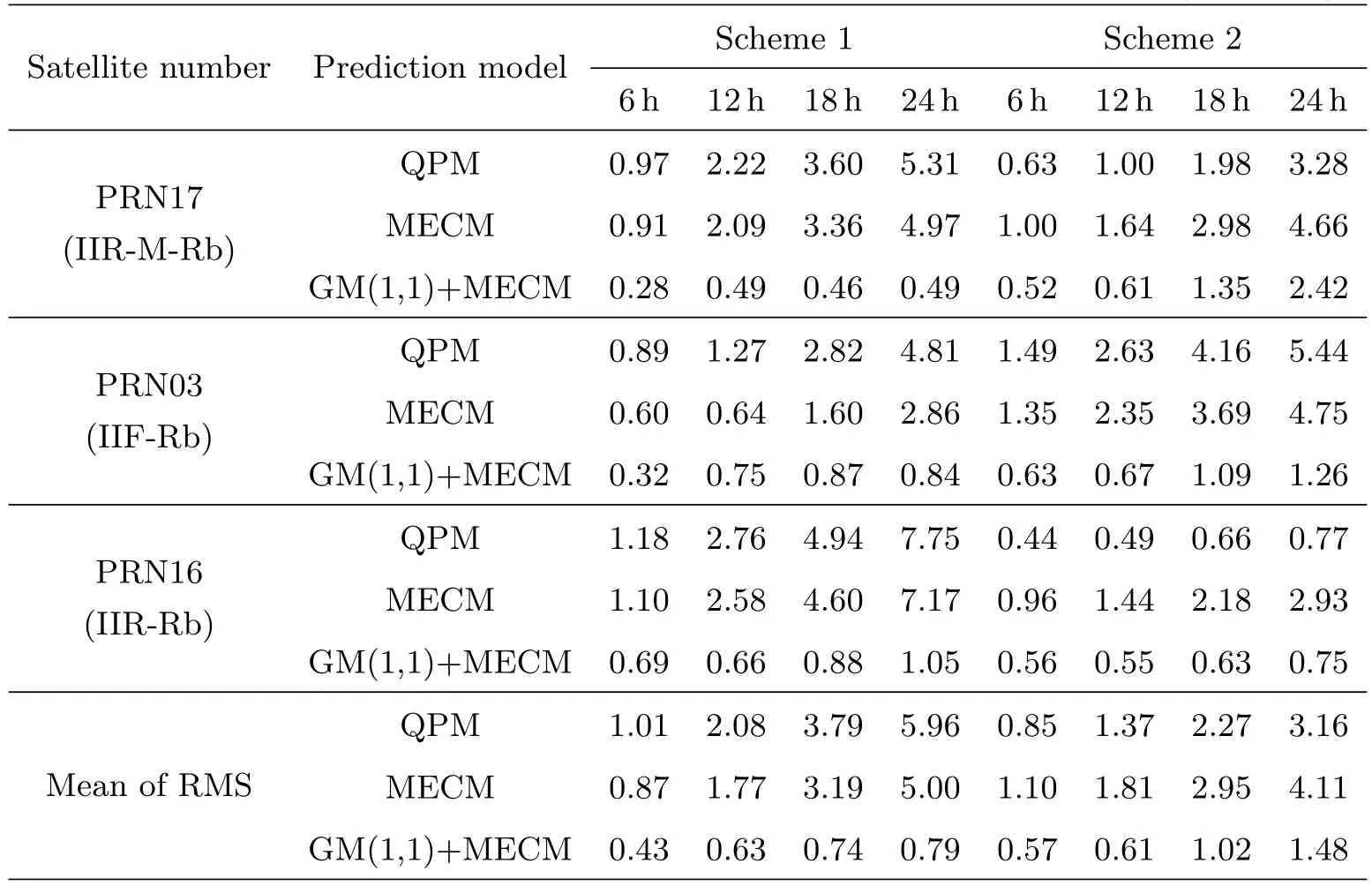
表1 精密卫星钟差预报结果的RMS(单位:ns)Table 1 RMS of pred iction results for precise satellite clock bias(unit:ns)

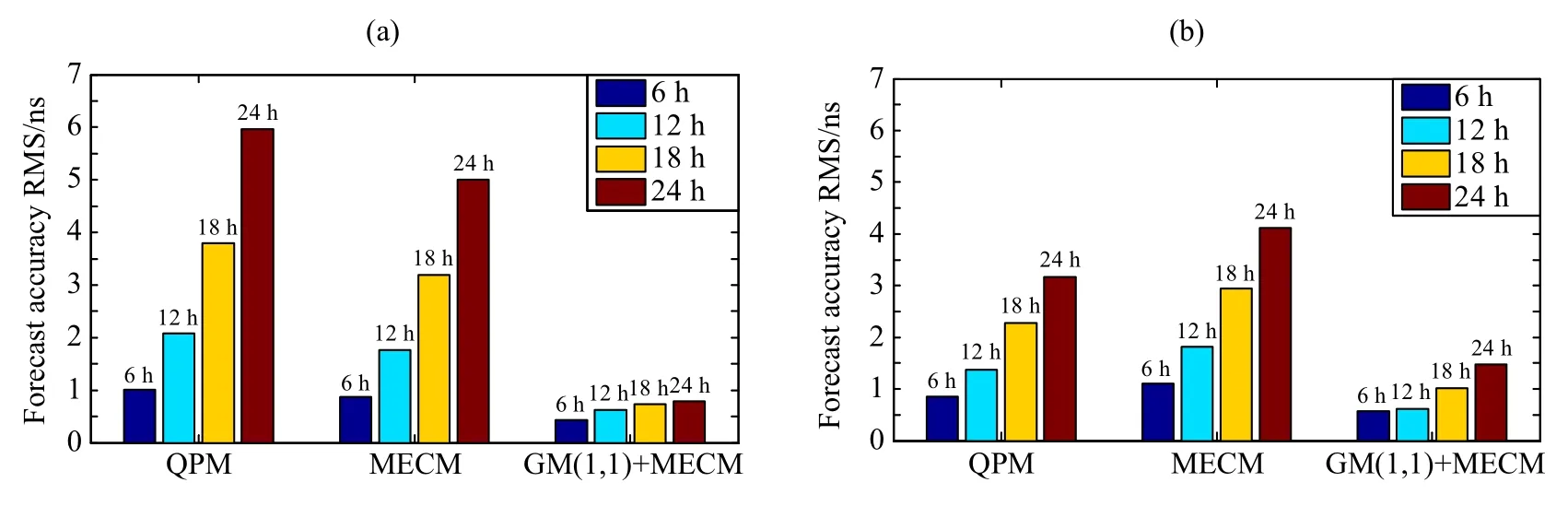
图8 方案一(a)和方案二(b)钟差预报精度比较Fig.8 Accuracy comparisons of clock bias prediction for scheme 1(a)and scheme 2(b)

结合图2–8和表1可知:

(1)采用小数据量(12h钟差数据)建模,对未来6h、12h、18h和24h的钟差进行预报时,二次多项式模型预报误差的平均均方差分别为1.01ns、2.08ns、3.79ns和5.96ns,修正指数曲线法模型预报误差的平均均方差分别为0.87ns、1.77ns、3.19ns和5.00ns,而基于GM(1,1)和MECM组合模型预报误差的平均均方差分别为0.43ns、0.63ns、0.74ns和0.79ns.

(2)采用中等数据量(24h钟差数据)建模,对未来6h、12h、18h和24h的钟差进行预报时,二次多项式模型预报误差的平均均方差分别为0.85ns、1.37ns、2.27ns和3.16ns,修正指数曲线法模型预报误差的平均均方差分别为1.10ns、1.81ns、2.95ns和4.11ns,而基于GM(1,1)和MECM组合模型预报误差的平均均方差分别为0.57ns、0.61ns、1.02ns和1.48ns.

(3)建模所采用的数据量的多少对二次多项式模型的预报性能有一定影响,建模所采用的数据量增大,二次多项式模型的预报性能有一定提升.建模所采用的数据量对修正指数曲线法模型的预报性能也有一定影响,建模所采用的数据量越大,修正指数曲线法的预报性能反而下降,这说明对于修正指数曲线法模型来说,不是建模所采用的数据量越多越好.而建模所采用的数据量的多少对基于GM(1,1)和MECM组合模型的预报性能影响较小,当增加一定量的建模数据时,基于GM(1,1)和MECM组合模型的预报性能变化很小,依然能够进行高精度的中短期预报.

4 结语

针对卫星钟差呈现趋势项和随机项变化的特点,本文提出了基于GM(1,1)和MECM的组合预报模型.该模型首先采用GM(1,1)预报钟差的趋势项,然后利用MECM模型对GM(1,1)模型残差序列进行建模和预报,最后将GM(1,1)和MECM模型的预报结果对应相加得到卫星钟差的最终预报值.这种组合模型可以把两种模型的预报优势有机地结合起来,进一步提高了模型的预报性能,从而提高了卫星钟差预报的精度.经理论和预报试验分析,结果也表明了该组合模型的有效性和可行性.