地-月系平动点轨道的特征及其相关问题
刘 林汤靖师侯锡云
(1南京大学天文与空间科学学院南京210046)
(2南京大学空间环境与航天动力学研究所南京210093)
1 引言
关于定点在地-月系共线平动点附近的探测器轨道外推(或称预报)问题,并不是一个新问题,该类型的飞行器,实际上就是一颗带有一定轨道特征的远地卫星.但是,尽管理论上绕地运行周期与月球一致,但它受到的月球引力影响却不是一个小扰动,而是一个几乎与地球引力作用同等重要的外力源.因此,该问题也无法处理成一个简单的受摄二体问题.如果仍然像构造平动点特殊轨道(如晕轨道)问题那样,在地-月系中来处理该问题,也无法像卫星运动那样处理成一个简单的受摄二体问题,其难点有如下两个方面:
(1)即使基本模型采用简单的圆型限制性三体问题[1−3],其基本解也较复杂.如果考虑月球轨道偏心率,处理成椭圆型限制性三体问题,不仅基本解更复杂,而且无济于事.因为太阳引力摄动影响与月球轨道偏心率的效应相当,无论采用上述哪类基本模型,要在此基础上构造摄动解,都不可能像一般受摄二体问题那样简单,无法满足实际应用的需求.
(2)即使形式上处理成一般的受摄二体问题,但由于探测器到月球的距离与探测器到地球的距离相当,这是处理第三体摄动问题的一个难点.
鉴于上述分析,对于地面测控而言,宜在J2000地心天球坐标系中采用数值方法实现地-月系平动点探测器的轨道外推,其数学模型就是一个表面形式上的受摄二体问题,状态运动方程如下:
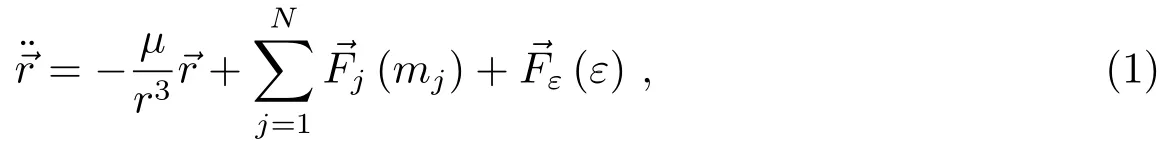
2 外力分析
对于航天器的轨道外推问题,实为一个定量问题,因涉及的各物理量有不同的量纲和大小,不便于问题的分析和表达,拟采用无量纲单位(可简称为归一化单位)来处理问题.以地球卫星的轨道运动为背景,包括月球之类的远地卫星(如地-月系的L1或L2点探测器)轨道,通常采用的归一化单位系统,即长度单位[L]、质量单位[M]和时间单位[T]如下:
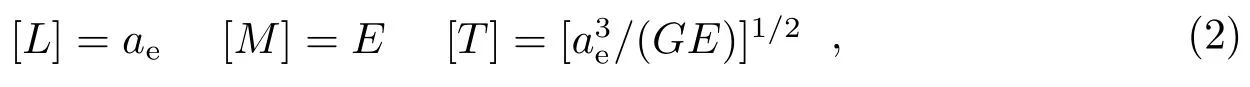
其中,GE是地心引力常数,ae是地球参考椭球体的赤道半径,时间单位[T]是导出单位,目的是使该计算单位系统中,引力常数G=1和中心天体引力常数µ=GE=1.如果地球引力模型采用当今地固坐标系所对应的WGS-84系统,则相应的地球动力学扁率为J2=1.082636022×10−3.
在采用上述归一化单位后,状态运动方程(1)式变为下列形式:
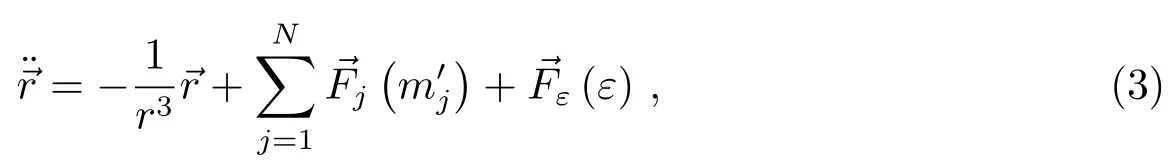
该式中的是月球、太阳等第三体的无量纲质量,即
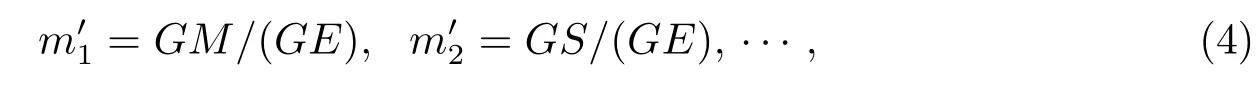
其中,GM和GS分别为月心和日心引力常数.
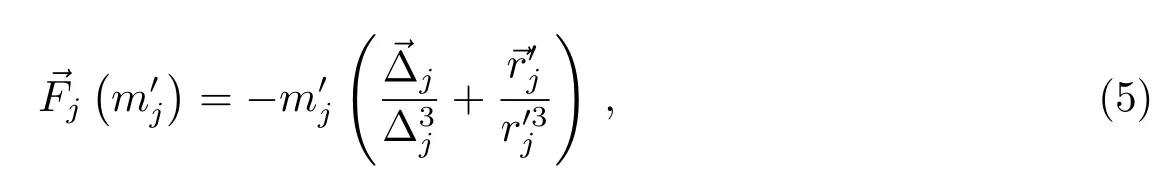
其中,是航天器到第j个天体的位置矢量,是航天器到第j个天体的距离,是地心天球坐标系中月球、太阳等第三体坐标矢量.
2.1 各大天体的引力摄动量级估计
地球的引力常数即GE=398600.4418 km3/s2,而月球、太阳、水星、金星、火星、木星和土星的引力常数相对地球的大小依次分别为0.0123000383、332946.050895、0.055273598、0.814998108、0.107446732、317.8942053和95.1574041.
摄动量级的近似估计式为

该式中的即各大天体相对地球的质量比,其值即上面给出的引力常数比,r和分别为探测器和摄动天体到地球的距离,估计中可取的平均值,但因水星轨道的偏心率较大(e>0.2),对应的r′值将分别按近日点和远日点两种状态设定平均距离.
考虑定点在地-月系共线平动点L1和L2的探测器到地球的距离r分别为

其中是地-月平均距离.由(6)式给出上述各大天体对L1和L2点探测器轨道的摄动量级分别如下:

2.2 地球非球形引力摄动量级
主项(扁率J2)的摄动量级估计
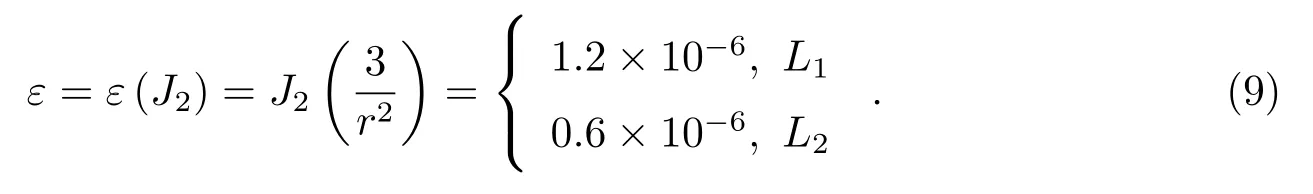
2.3 太阳光压的摄动量级
定点在地-月系共线平动点L1和L2的一个通常尺度(包括质量和承受光压的等效截面)的探测器,太阳光压摄动的量级估计如下:

其中,κ=1.44,面质比S/m=109,ρ⊙为1 au处的太阳辐射压强,ρ⊙=0.3169×10−17.
根据上述对外力因素的量级估计,对于定点在地-月系共线平动点L1和L2或其附近的探测器轨道,若考虑10−6以上的摄动因素,相应的力模型中只需要考虑如下摄动源:月球、太阳和金星的质点引力,地球非球形引力位的扁率J2和太阳光压,其中最主要的是月球和太阳的质点引力.
3 定点在地-月系L1和L2点的探测器轨道概貌
这里给出地-月系圆型限制性三体问题模型下两个简单的算例,初始历元为2016-09-30UTC0:00:0.0,对应的TDT(地球力学时)是57661.0007891667(MJD),探测器定点在地-月系L1和L2点的各一条轨道上.经简单坐标转换,即可获得J2000.0地心天球坐标系中相应的两条轨道的初始位置(x,y,z)、速度(˙x,˙y,˙z)和相应的轨道根数,分别列于表1和表2.

表1L 1点和L 2点的位置和速度Table 1 The positions and velocities of the points L1 and L2

表2L 1点和L 2点的轨道根数Table 2 The orbital elements of the points L1 and L2
两条轨道的图像见图1–2,这表明在初始时刻瞬间,实际上都是一条偏心率较大的环绕地球的椭圆轨道,探测器均处于该轨道的远地点和近地点(对读者而言,这一特点是容易理解的,无需做过多解释),两图中的坐标单位ae是地球参考椭球体的赤道半径.就地-月+探测器系统而言,这都是初始瞬时轨道,而在月球的引力作用下,探测器与月球轨道“同步”做相同的圆轨道运动.
4 平动点轨道外推问题的相关分析
4.1 平动点轨道分析采用的数学模型
第1节引言中已指出,应在J2000地心天球坐标系中处理其轨道运动问题,并采用数值方法实现相应的轨道外推.为了定量显示这类轨道外推中误差传播状态的主要特征,显然应选择地-月-日+探测器的质点引力系统,相应的状态运动方程即
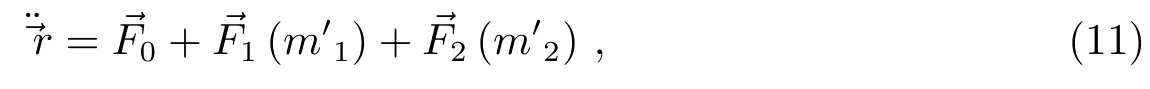
其中是地球引力加速度:而和分别为月球和太阳的无量纲质量,见前面的(4)式.相应的月球和太阳引力摄动加速度、的具体形式分别为
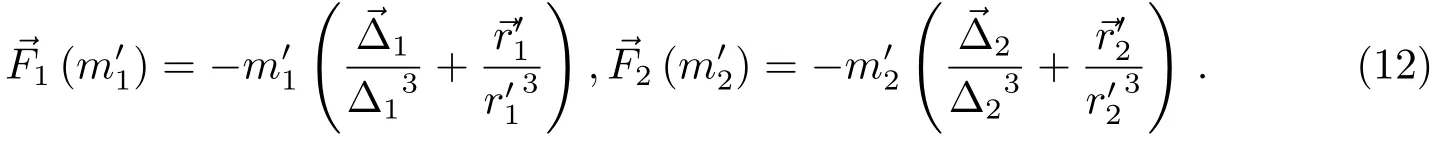
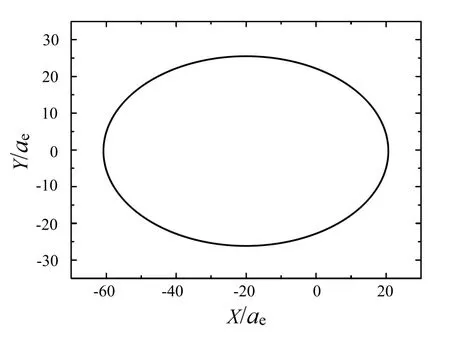
图1L1点初始轨道在J2000地心天球坐标系中(赤道面内)的图像Fig.1 The figure(in the equatorial plane)of point L1initial orbit in the J2000 reference system

图2L 2点初始轨道在J2000地心天球坐标系中(赤道面内)的图像Fig.2 The figure(in the equatorial plane)of pointL 2initial orbit in the J2000 reference system
4.2 平动点轨道类型的选择
这里考查的平动点轨道,包括如下3种类型:
(1)初始时刻定点在地-月系的L1点或L2点处的平动点轨道,以下简称该类型轨道为L1点轨道或L2点轨道;
(2)初始时刻定点在地-月系的L1点或L2点附近的halo轨道上,以下简称该类型轨道为L1点晕轨道或L2点晕轨道;
(3)初始时刻定点在地-月系的L1点或L2点附近的Lissajous轨道上,以下简称该类型轨道为L1点Lissajous轨道或L2点Lissajous轨道.
经初步设计(对应所采用的质点引力系统)分别给出6条轨道,在J2000地心天球坐标系中各对应的轨道初值如下:所有初始时刻对应历元为2016-09-30UTC0:00:0.0(相应TDT的MJD为57661.0007891667),位置、速度和相应的轨道根数分别列于表3和表4.表中的轨道类型1、2、···、6依次为L1点轨道、L1点晕轨道、L1点Lissajous轨道、L2点轨道、L2点晕轨道、L2点Lissajous轨道,表4–8类同.
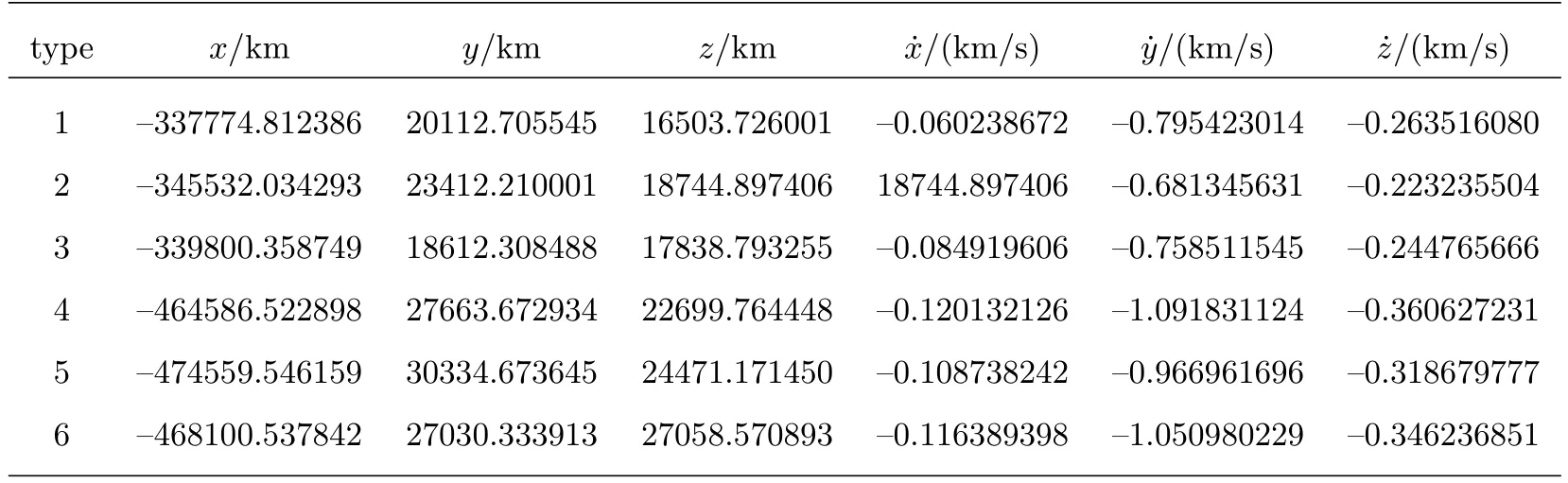
表3 6条轨道的位置和速度Table 3 The positions and velocities of 6 oribits
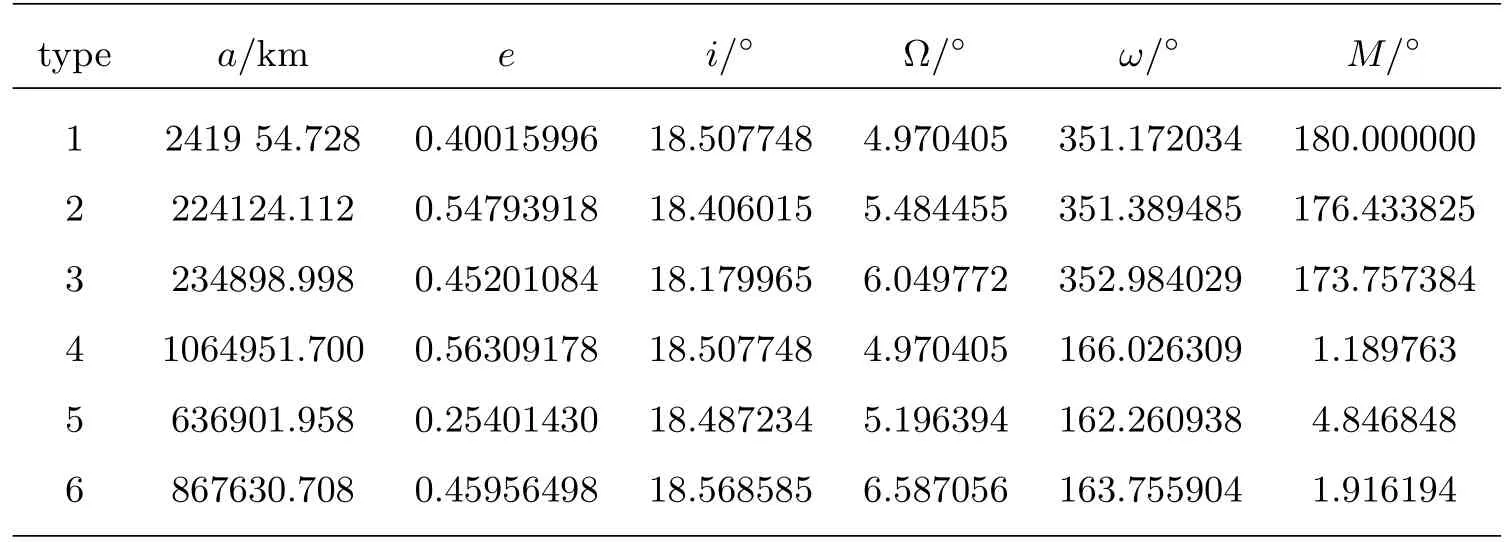
表4 6条轨道的轨道根数Table 4 The orbital elements of 6 oribits
下面首先对上述6类轨道作7d和27d的轨道外推,给出一个误差传播的定量轮廓,在此基础上再作定性分析.
4.3 6条平动点轨道外推7d的状态
为简单起见(也不失一般性),在考查误差传播中,将初始误差全部集中在最重要的轨道半长径上(根据目前定轨的实际状况,轨道半长径的精度为10 m量级),7d的轨道外推结果列于表5–6.
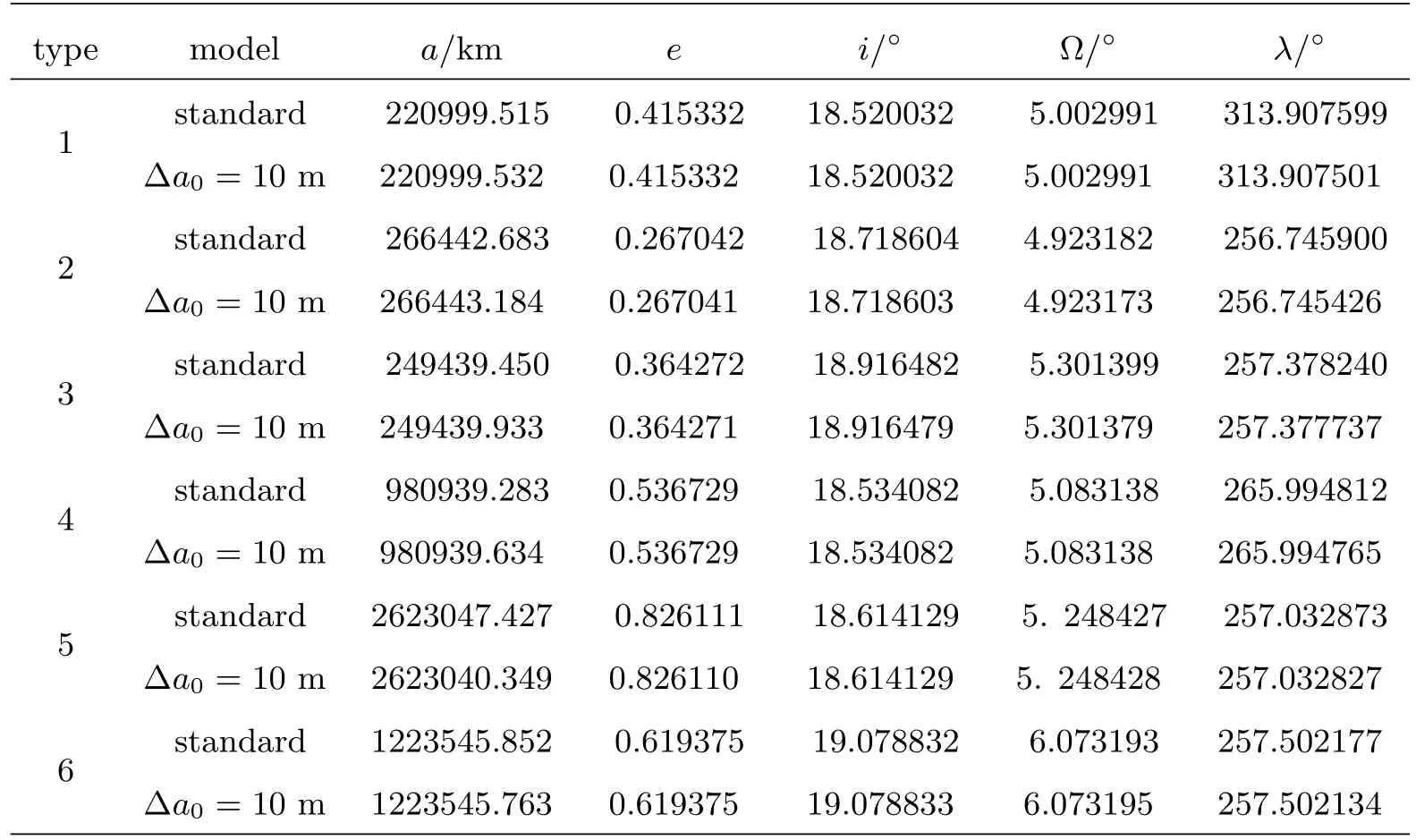
表5 平动点轨道外推7d的轨道状态Table 5 The states of the libration point orbits propagated for 7days
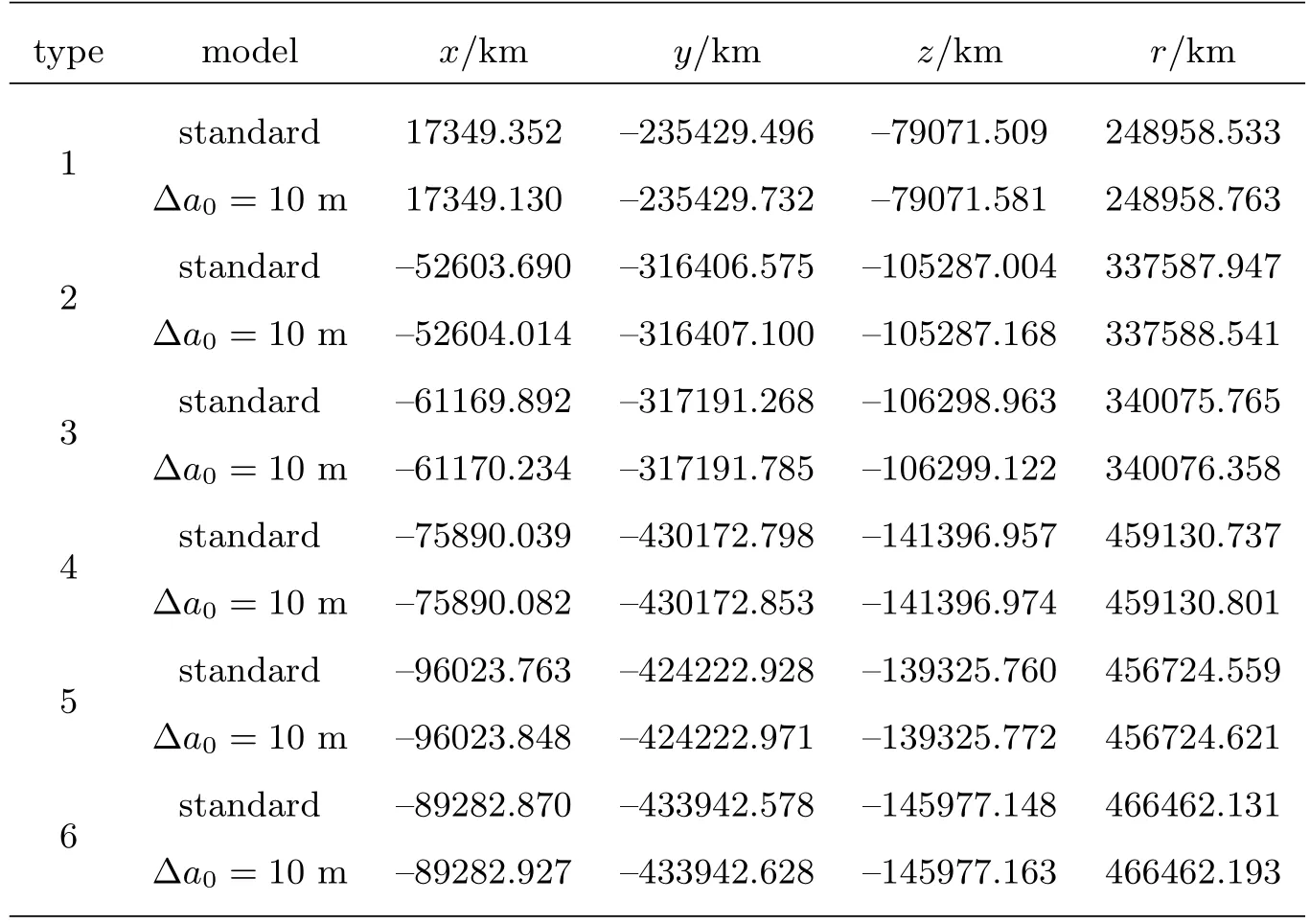
表6 平动点轨道外推7d的空间位置状态Table 6 The positions of the libration point orbits prop a gated for 7days
4.4 6条轨道外推27d的状态
尽管探测器的定点只是近似的,实际运行过程中必须通过不断轨控才能保持这类轨道,外推弧段增长至27d,只是为了进一步了解这类特殊轨道的动力学特征及其相应的误差传播规律.初始误差仍全部集中在轨道半长径上,27d的轨道外推结果列于表7–8,其中,第2和3两类轨道(即L1点晕轨道和L1点Lissajous轨道)只外推了22 d,其原因将在4.5小节中具体说明.
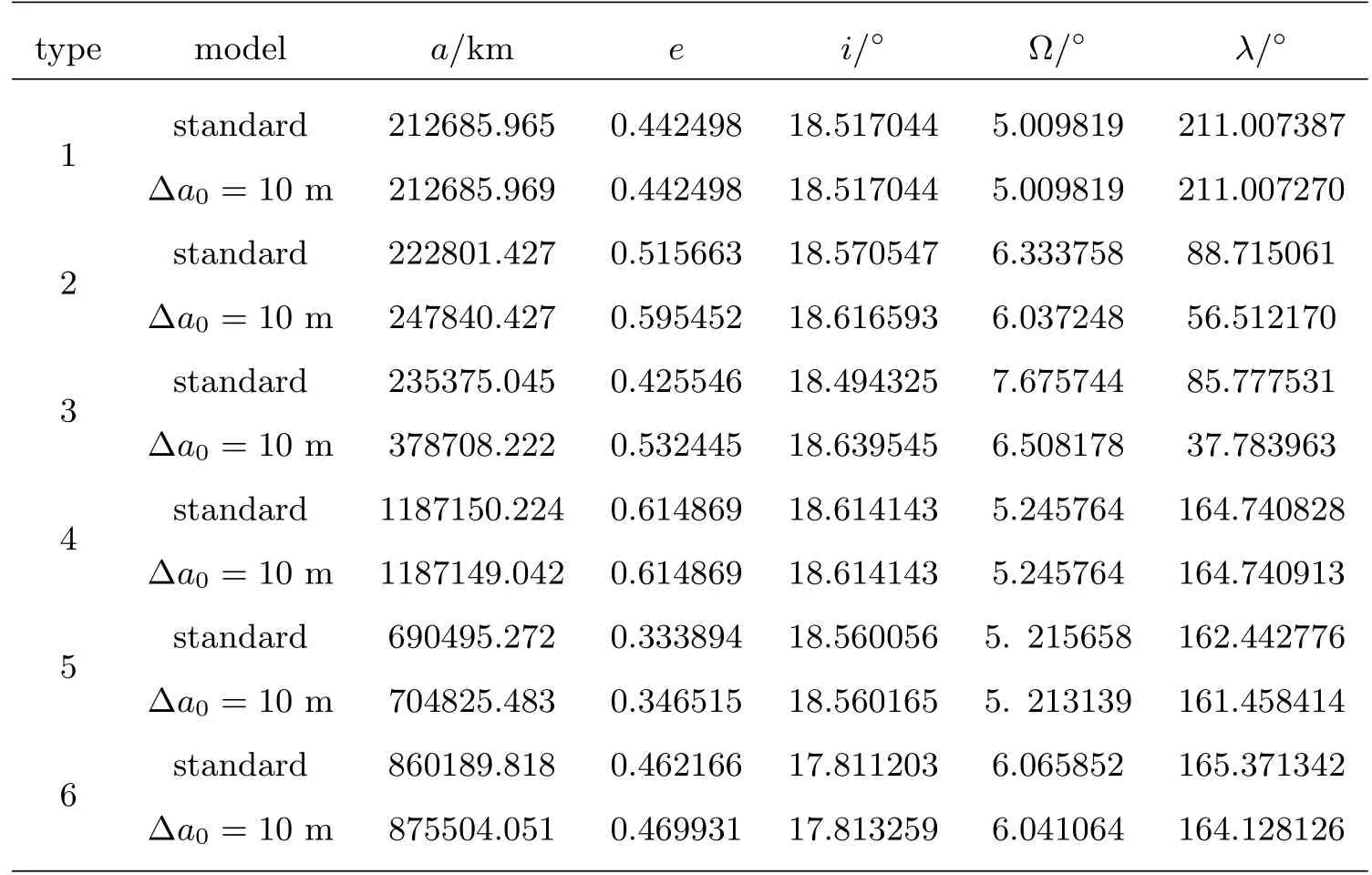
表7 平动点轨道外推27d的轨道状态Table 7 The states of the libration point orbits propagated for 27days
对于探测器的轨道运动而言,通常所说的长期位置预报和短期位置预报中的长期或短期并不是简单的时间间隔,而是运行弧段的长短.因此,为了比较上述各条轨道之间外推误差传播的定量大小,需要了解它们的轨道运行周期,这6条特殊轨道的初始运行周期TS值依次为
L1类:TS=13.708768 d,12.221658 d,13.113512 d;
L2类:TS=126.58784 d,58.847196 d,93.089267d.
由此便于了解轨道外推7d和27d对上述6条轨道所对应的弧段长短.
在已知6条轨道自身的动力学特性和轨道外推弧段长短的前提下,不难看出表5所列出的外推位置误差所反映的一些动力学规律,基本上可归纳如下:
(1)轨道外推7d均为短弧,位置误差都在1 km以内;
(2)对于L1点轨道和L2点轨道,外推7d或27d,位置误差的累积仍不严重,其误差传播的特征就是一般Kepler运动特征的反映.由于初值误差(∆a0=10 m)较小,实为小扰动,既不会激发其初值不稳定的固有特征,又不会明显改变短弧段误差累积的效果,反而周期性的效果比长期累积效应更明显,见表5中轨道1(即L1点轨道)的误差定量状态.
(3)对于L1点和L2点的halo轨道和Lissajous轨道而言,由于其位置已经“远离”不稳定平动点L1和L2,而严格的halo轨道和Lissajous轨道设计又无法实现,探测器的定点只是近似的,在同样是∆a0=10 m的初值误差情况下,已不能再简单地只看作对halo轨道和Lissajous轨道的小扰动,而更重要的是对平动点的大扰动起作用,在不太长的外推弧段内,其平动点本身的不稳定特征即显现无遗.见表5中的轨道2、轨道3、轨道5和轨道6,特别是轨道2和3,相对而言,27d的弧段显得更长,外推弧段超过22 d后,其轨道偏心率很快就会达到e≈1.0的状态.
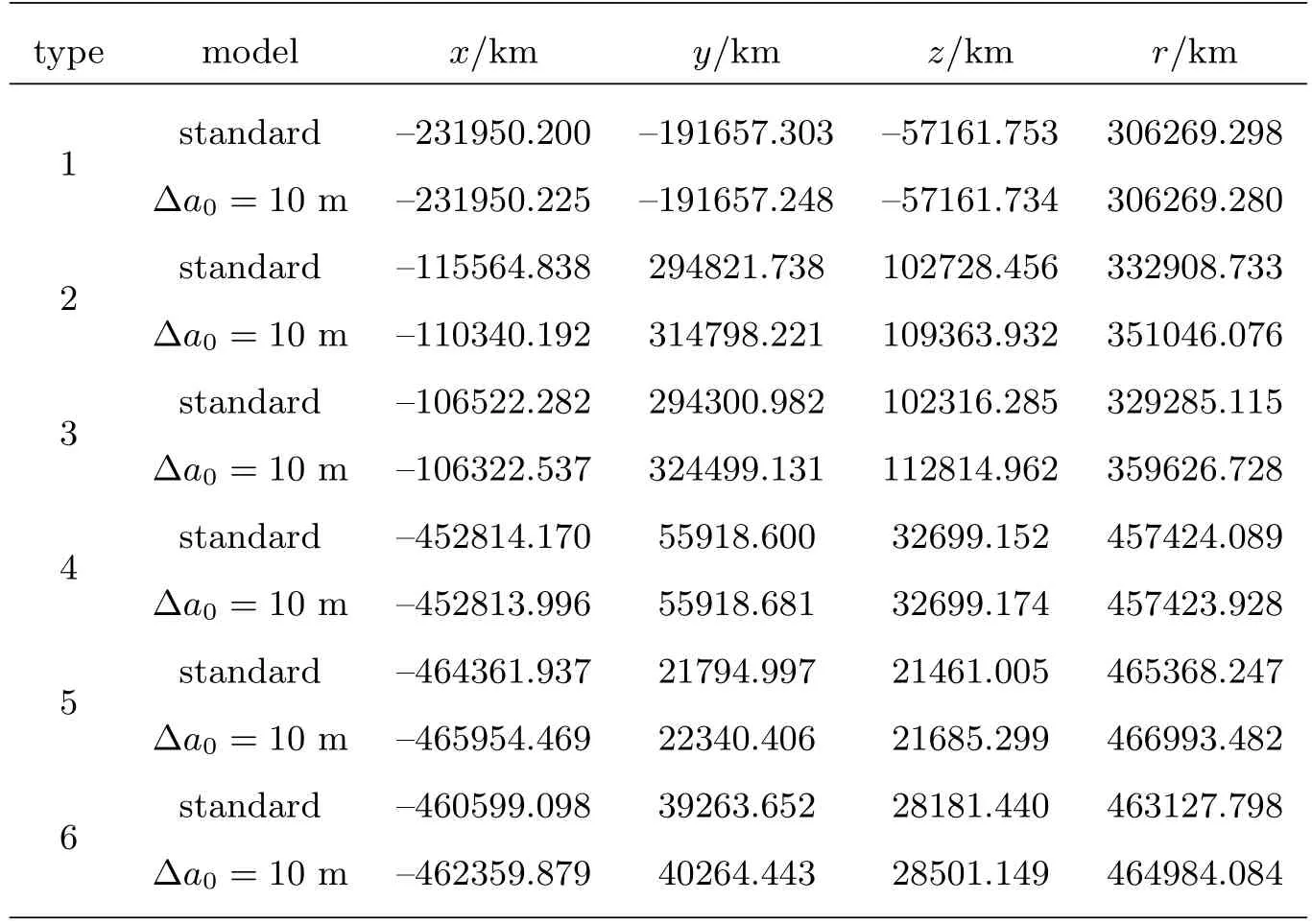
表8 平动点轨道外推27d的空间位置状态Table 8 The positions of the libration point orbits propagated for 27days
4.5 平动点轨道运行中误差传播状态的基本特征
从上述6条轨道的外推计算结果已能看出拉格朗日点轨道外推中位置误差传播的基本特征,首先将由∆a0=10 m导致的位置误差集中列于表9.

表9 拉格朗日点轨道外推位置误差的定量状态(单位:km)Table 9 The quantitative state of position error s of the Lagrange point orbit propagation(unit:km)
综上几小节,就平动点探测器轨道运行误差传播状态的简单计算和分析,可以表明:在地-月系L1和L2平动点轨道设计中,确实很难实现较长弧段的无动力控制运行轨道,而不是设计者本身的问题.那么,在这样较短的弧段内,就轨道预报而言,要达到较高的精度是容易实现的,本节最后一小节将会给出具体算例,并有实测结果的检验.
4.6L1点晕轨道的运行状态
为了进一步揭示平动点飞行器轨道外推中误差传播的动力学机制,这里再给出一条与上述L1点晕轨道相近的环绕地球运行的大椭圆逆行轨道,同样对应一远地卫星.初始时刻仍为2016-09-30UTC0:00:0.0,初始位置和速度及相应的轨道根数分别列于表10和表11.该轨道的初始运行周期为12.208831 d.对此轨道同作27d的外推,计算结果列于表12–13.

表10L1点晕轨道的位置和速度Table 10 The position and velocity of the halo orbit at pointL 1

表11L 1点晕轨道的轨道根数Table 11 The orbital elements of the halo or bit at pointL 1

表12L 1点晕轨道外推27d的轨道状态Table 12 The states of the halo orbit prop a gated for 27days at pointL 1

表13L 1点晕轨道外推27d的空间位置状态Table 13 The positions of the halo orbit prop a gated for 27days at pointL 1
这样一条有别于L1点晕轨道绕地运行的大椭圆逆行轨道,本质上就是一条普通的Kepler轨道,其固有的初值不稳定性在绕地运行27d(仅2圈)的短弧内不会有明显体现,这是一个常规问题,本文引进这一算例的目的,是从另一角度体现地-月系平动点轨道误差快速传播的固有不稳定性特征.至于逆行轨道自身的运动规律及其动力学特征,已超出本文论述的范畴,不再介绍,如有需要,可见文献[4]及其有关作者的研究工作.
4.7 平动点轨道的定轨和短弧预报精度的检验
既然严格的拉格朗日点轨道设计无法实现,探测器的定点只是近似的,运行过程中必须通过不断的轨控才能保持,那么,对于地面测控和星上控制,只能从短弧角度来考虑问题.
对于平动点轨道的短弧定轨和轨道预报而言,相对地球低轨或高轨卫星的同类问题,实无任何特殊困难和特别需要处理的难题.采用南京大学空间环境与航天动力学研究所自主编写的定轨软件和利用国内的USB(Unified S-band)测量数据,在没有任何其他辅助信息的前提下,对嫦娥3号的相关任务探测器进行了定轨,并与北京航天飞行控制中心的事后定轨结果作了对比.在此定轨的基础上,采用非常简单的数值外推方法(只考虑地、月、日三体的质点引力和简单的光压模型,外推中的6个轨道初值采用相关任务的定轨结果)进行了轨道预报,毫无困难地达到了较高精度.略去不必要的细节说明,将有关结果一并列于表14–15.

表14L 2点晕轨道短弧外推3 d与事后精密定轨结果的比较Table 14 The comparison of two precise orbit determination method s for the pointL 2orbit after propagating 3 days

表15L 2点晕轨道短弧外推7d与事后精密定轨结果的比较Table 15 The comparison of two precise orbit determination methods for the pointL 2orbit after prop a gating 7days
表14–15中的精密定轨A和B分别对应北京航天飞行控制中心和南京大学空间环境与航天动力学研究所的结果,表中的结果基本上已能说明问题,但为了让读者对这类探测器的定轨和外推精度有更清晰的了解,下面进一步作些必要的说明.
(1)关于光压模型,在不了解探测器的具体细节情况下,作者们根据独立定轨中获得的有关估计值,获得了包括卫星表面热性能在内的等效面质比,从而给出了相应的经验模型:一个等效的平面模型.
(2)尽管没有具体给出两个单位的定轨(包括测量数据)细节,但表14–15所给出的计算结果,已能说明本文要体现的这类特殊轨道的定轨和外推精度了.因为表中的结果是外推3 d和7d与事后精密定轨结果的比较,且两个单位的定轨结果之差基本上在500 m之内,这样的比较更能体现两个单位定轨结果的真实性以及本文所采用的力模型的合理性.
上述计算结果和两点补充说明充分表明:尽管这类探测器的轨道特殊,初值误差的传播程度远比一般的环绕型探测器的轨道显著,但相应的短弧定轨和高精度轨道预报并无特殊困难.
4.8 关于两种坐标系中平动点探测器轨道形式的转换问题
就定轨和预报的需求,显然是在J2000地心天球坐标系中进行相关问题的处理,而对这类具有特殊性质的轨道,轨控又必须通过相应的地-月系旋转坐标系来处理.这就涉及到两种坐标系之间的转换问题,其本身是容易实现的,而在具体的航天任务中,各有关部门根据实际需求,对相应的地-月系旋转坐标系实有不同取法,故这里不再做相应讨论.

