“毕达哥拉斯树”教学研究报告

一、问题

“毕达哥拉斯树”这一教学内容源自人教版数学教材五年级上册总复习单元中的一道思考题：一个直角三角形的三条边长分别是3cm、4cm、5cm。以这三条边分别为边长画三个正方形，这三个正方形的面积各是多少？通过研读教材，我们认为，教材的编写意图是让学生借助“以一个直角三角形的三条边为边长，分别向外作三个正方形”，发现这三个正方形面积之间的关系，进而研究直角三角形三边之间的关系，为今后中学学习勾股定理作铺垫。而勾股定理的证明，人教版教材安排在八年级下册。五年级的孩子研究这一高难度的内容，我们该如何把握好度？为此，我们进行了以下的思考与分析。

1.如果教学仅仅停留在解决“你能发现这三个正方形面积之间有什么关系吗”这一问题的层面，只需引导学生通过计算找出每组中三个正方形面积之间的关系即可，思维含量显然不够。如果拔高为勾股定理的证明，学生又难以理解。这节课的教学目标究竟该如何定位？

2.根據教材要求，以直角三角形的三条边为边长，分别向外作三个正方形，再计算它们的面积，对大部分学生来说非常简单。如何才能引导孩子们发现三个正方形面积之间的关系？并且发现在三角形中，唯有直角三角形才有此种关系？

3.对五年级学生来说，勾股定理非常抽象，难以理解。如何才能化抽象为具体，让学生经历完整的数学探究过程，形成解决实际问题的策略，培养研究事物的能力？

根据五年级学生现有的知识基础和思维水平，经过讨论，我们将本节课的教学目标定位为：通过面积证法，经历直角三角形三边关系的探索过程，发展学生的合情推理能力，体会数形结合的思想；通过介绍有关勾股定理的知识，拓展学生的视野，丰富学生的数学知识。

为了达成教学目标，我们通过查找资料，发现“毕达哥拉斯树”可以作为这一内容的探究素材，它是根据勾股定理画出来的一个可以无限重复的图形。因为重复数次后的形状好似一棵树，所以被称为“毕达哥拉斯树”，也叫“勾股树”。借助这一素材，教师通过设计基于学情的研究活动，引导孩子们经历“观察—发现—猜测—验证—得出结论”的全过程，让他们真正成为数学知识的研究者、发现者。

二、实践

基于以上思考，我们对教材进行了创造性处理，将一道习题设计成一堂兼具数学味、思维味、文化味的新授课。主要教学过程如下：

（一）情境导入

师：同学们，老师给大家带来了一棵树，它叫毕达哥拉斯树。（板书课题）大家有什么问题吗？

生1：毕达哥拉斯树是什么意思？

生2：数学课为什么要看树？

师：是啊，这棵树与我们数学有什么关系呢？今天我们一起走近神奇的毕达哥拉斯树。

（二）探索新知

1.观察树，发现数学特征

师：毕达哥拉斯树马上要华丽登场了，请大家仔细观察。（课件演示树的动态形成过程，如图1所示）

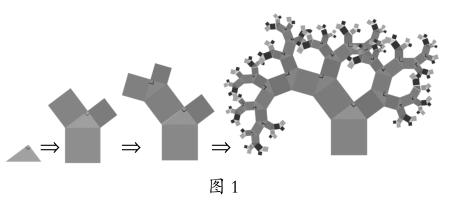
生（惊叫）：哇，好漂亮……

师：你们有什么发现？

生3：我发现这棵树全是由正方形和三角形组成的。

师：用数学的眼光看世界，真棒！

生4：我发现这棵树上的三角形全都是直角三角形。

师：你是怎么发现的？

生4：这些三角形中都有一个角标上了直角符号，说明它们全是直角三角形。

师：好一双善于发现的眼睛！

生5：我发现这棵树上正方形和直角三角形的排列是有规律的，每个直角三角形的周围都有三个正方形。

师：真像他说的这样吗？我们一起看一看。（师生一起逐组观察验证）确实！正是这样一组一组的图形排列在一起，就形成了一棵茂盛的毕达哥拉斯树。每组中一个直角三角形周围都有三个正方形，我们既可以看成是以直角三角形的三条边为边长，分别向外作出的三个正方形，也可以看作是由三个正方形用边长首尾相连围成的一个直角三角形。那是不是任意三个正方形的边长首尾顺次连接，都能像这样围成一个直角三角形呢？为什么？

生6：肯定不是！你看，围成大三角形的三个正方形明显就大一些，围成小三角形的三个正方形明显就小一些。要是随便对换一下，肯定围不成的。

师：看来三个正方形能否围成一个直角三角形，与正方形的大小是有关系的。每一组中三个正方形的大小究竟是什么关系呢？（学生要求选一组进行研究）从哪一组开始研究比较好呢？

生7：我觉得可以选树干最下面三个最大的正方形围成一个直角三角形这一组，因为这棵树是从这一组开始长成的。

师：这个方法可真好！我们遇到像这样比较复杂的问题时，可以从它最基本的组成元素开始研究。

2.研究规律

生14：我觉得，如果三个正方形之间存在S甲+S乙=S丙的关系，用这三个正方形的边长就一定能围成一个直角三角形。（其他学生同意他的说法）

师：这种猜想是否正确呢？我们怎样验证？

生15：我觉得可以先随意画更多的直角三角形，量出它们的边长，再算一算，看是否全部符合S甲+S乙=S丙的关系。

生16：还可以把两个不同大小的正方形沿着直角边摆好，然后算一算边长用来做斜边的正方形面积应该是多少，再找到这个正方形，实际摆一摆验证一下。

师：你们想的办法都非常好。老师为每组准备了大小不同的若干正方形，还有一张画有直角的练习纸，请动手围一围、算一算，看能围成直角三角形的三个正方形之间是否存在S甲+S乙=S丙的关系。

学生研究之后汇报研究结果。

3.发现三边关系

师：如果用字母a、b、c分别表示甲、乙、丙的边长，那么这三个正方形面积之间的关系用字母怎样表示呢？（生17：a2+b2=c2）请仔细观察，我们将正方形的边长脱离出来。（课件演示）现在，在直角三角形中，a、b、c分别表示什么？

生18：a、b表示直角三角形的两条直角边，c表示直角三角形的斜边。

师：说得对！那a2+b2=c2在直角三角形中表示什么？

生19：一条直角边的平方加另一条直角边的平方等于斜边的平方。

师：一条直角边的平方加另一条直角边的平方可以简说成两直角边的平方和。（板书）刚才我们得到这个关系式的前提条件是什么？

生（齐）：直角三角形。

教师完善板书：在直角三角形中，两直角边的平方和等于斜边的平方。学生齐读结论。

4.研究规律的适用范围

师：刚才我们探究出直角三角形三边关系是a2+b2=c2。看到这个结论，你们还有什么疑问吗？

生：钝角三角形和锐角三角形中，是否也存在a2+b2=c2这种三边关系呢？a2+b2=c2这种三边关系是不是直角三角形独有的呢？

师：你们的问题提得很有价值！大家想一想，直角三角形的三边关系a2+b2=c2在钝角三角形和锐角三角形中是否也适用呢？

生20：我觉得应该适用，因为它们都是三角形，都有三条边。

生21：我觉得不适用，因为直角三角形中有直角，而钝角三角形和锐角三角形中没有，它们不一样。

师：究竟谁说得对呢？我们用什么办法验证？

生22：我们可以像研究毕达哥拉斯树上的每组图形一样，画一些钝角三角形和锐角三角形，量一量、算一算，看看是否也有这样的关系。

师：大家觉得这种研究方法怎么样？

生23：我认为不好。太麻烦了！我觉得可以利用刚才老师发给我们的学具进行想象。比方说，我们已经研究出这一组三个正方形可以摆成一个直角三角形。（边摆边说）现在把两条直角边稍微挪动，使它变成一个锐角（或者变成钝角），这样就将直角三角形变成了一个锐角三角形（或者钝角三角形）了。（师：对）现在再看原来的斜边，变成锐角三角形后，原来的斜边就变短了，变成钝角三角形后，原来的斜边又变长了，所以锐角三角形与钝角三角形中都没有这样的三边关系；只有直角三角形存在a2+b2=c2的三边关系。（全场掌声雷动）

（三）了解数学文化

师：同学们，今天我们通过对毕达哥拉斯树进行观察、研究，借助正方形的面积，探究出在直角三角形中，两直角边的平方和等于斜边的平方。你们知道吗？我们探究出的直角三角形三边关系是数学史上非常著名的一个定理———毕达哥拉斯定理。相传最早发现这条定理的是古希腊著名的数学家毕达哥拉斯。他是怎样发现的呢？我们一起来听听他的故事。（课件播放故事）

师：刚刚上课的时候，有同学提出疑问：毕达哥拉斯树是什么意思？现在你找到问题的答案了吗？（生1：知道了）那你说说你的理解。

生1：因为这棵树是运用毕达哥拉斯定理画出来的。

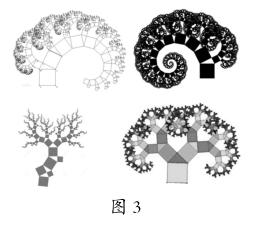
师：说得对！老师这里收集了很多毕达哥拉斯树的图片（出示图3）。这些树虽然大小不同、形状各异，但都是运用毕达哥拉斯定理画出来的。早在三千多年前，我国数学家商高就提出“勾三、股四、弦五”，所以毕达哥拉斯定理在我国也叫勾股定理，或者商高定理。在今后的数学学习中，我们还要进一步学习和研究。

三、讨论

郑毓信教授曾说：“如果您的教学始终只是停留于知识与技能的层面，您恐怕就只能算是一个教书匠；如果您的教学能够很好地体现数学的思维，您就是一个智者，您给学生带来了真正的智慧；然而，如果您的数学教学能给学生无形的文化熏陶，那么，即使您只是一个小学教师，即使您身处偏僻的深山或边远地区，您却是一个真正的大师，您的生命也因此而充满了真正的价值。”正是基于这样的认识，我们工作室认为，数学课堂应当是具有数学味、思维味和文化味的“三味课堂”。

在毕达哥拉斯树一课的研究中，我们借助美观奇妙的毕达哥拉斯树作为直角三角形三边关系研究的载体，整个教学紧紧围绕引导学生探寻直角三角形三边关系展开，毕达哥拉斯定理成为课堂教学显而易见的研究目标，呈现出明显的“数学味”。

在整个研究过程中，教师以毕达哥拉斯树引入，激发学生的学习兴趣，然后进行引导，逐步由扶到放：发现三个正方形能否围成一个直角三角形与正方形的大小有关系→研究有什么样的關系→发现毕达哥拉斯树上某一组围成直角三角形的三个正方形具有S甲+S乙=S丙的关系→研究是不是所有能围成直角三角形的三个正方形面积之间都存在这种关系→猜想怎样的三个正方形边长首尾顺次连接一定能围成一个直角三角形→研究这种三边关系是否是直角三角形独有的。孩子们通过观察、猜想、归纳、验证、迁移、质疑、反思，紧扣直角三角形三边关系这一核心内容，发现问题、提出问题、分析问题、解决问题，如数学家般亲身经历了定理的发生发展全过程，感受了数学思想的魅力，增长了智慧，让整个课堂充满了浓浓的思维味。

全课以毕达哥拉斯树开场，又以毕达哥拉斯树结束，前后照应，形成了课堂结构之美。尤其是多姿多彩的毕达哥拉斯树的欣赏，以及毕达哥拉斯定理、勾股定理的介绍，让孩子们拓宽了视野，增长了见识，数学文化在孩子们的心田悄悄地扎根。

（此文系湖南省教育科学“十三五”规划一般资助课题“小学数学‘三味课堂研究”课题阶段性成果，课题批准号：XJK016BZXX034）

（执笔人：谭念君、张新珏、徐旺、李闯）