拓扑优化及配套技术在转向系统固有频率调整中的应用

崔朝军

(厦门金龙联合汽车工业有限公司，福建厦门 361023)

我司某中型客车(四缸机)在怠速工况下，方向盘发生剧烈抖动。在怠速不开空调工况下，发动机的激励频率为22 Hz(发动机转速为660 r/min)，而由测试结果可知，转向系统的固有频率为21.9 Hz，即此时转向系统发生共振。为解决此问题，需调整转向系统的固有频率。在怠速开空调工况下，发动机的激励频率为26.7 Hz(发动机转速为800 r/min)，为满足NVH避频要求，需要将转向系统的固有频率调整到超过发动机的怠速激励频率2 Hz及以上。初步调整结构并进行测试发现:固有频率调整至24 Hz时，方向盘的振动情况仍不能满足要求，故频率调整目标只能定为28.7 Hz及之上。因频率上调整达7 Hz之多，根据经验采用一般的结构改进设计方法费时费力，所以将拓扑优化技术引入到此车型的转向系统固有频率的调整分析中。为保证拓扑优化能快速、有效地进行，引入了超级单元技术、系统固有频率的快速识别技术。

1 引入超级单元的模型处理

拓扑优化是在有限元软件多次计算结果的基础上，采用优化理论进行结构的寻优，因此每次有限元计算所占用的时间是制约优化分析效率的最主要因素。本文通过在模型处理中引入超级单元技术，加快计算速度，以提高拓扑优化的效率。以下是该中型客车引入超级单元的简要过程。

对该车的实体模型(包括骨架、内饰、外饰及底盘件)在HyperMesh中进行离散，其中车身及车架的主体结构采用2D壳单元，焊接部分采用RB3及六面体单元。经处理后得到总单元数1 229 663个，节点数1 288 739个，其中三角形单元占单元总数的百分比为0.4%。常规分析采用的有限元数模型如图1所示(只显示骨架模型和转向系统)。

将图1中的整车模型划分为2个部分:一部分为关注区域的模型(用于后续的结构优化，其包括转向系统及修改转向系统所涉及的区域，如图2所示);另一部分为关注区域之外的其他所有部分的模型(如图3所示，即图1代表的整车模型减去图2模型后剩余的模型)，要确保2个部分的单元与节点的编号不出现重合(除2个模型在断开位置处的，即2个模型通过相同的节点编号及空间坐标信息进行连接)。在图3所示的模型中(在OptiSstuct模块下进行如下设置)，约束上述共有节点的6个自由度，将模态计算的上限频率控制在60 Hz(发动机怠速开空调激励频率的2倍为宜);为后续在整车中观察振型，可将骨架模型粗化掉(调用menu菜单下的Coarsen Mesh卡片，骨架单元设置为30 mm，质量点及蒙皮、玻璃等不关心部位的单元均删除掉)，并转为PLOTEL单元，通过MODEL卡片参与结果生成，再采用CMSMETH卡片，将该结构生成超级单元，计算结果存储了该结构在约束状态下的模态信息。进行结构改进时(图2所示的模型)，通过ASSIGN卡片调用超级单元结果(即图3模型生成的h3d类型文件)即可进行分析。

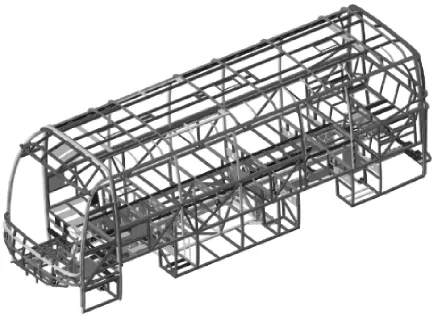
图1 转向系统频率计算的常规有限元整车模型

图2 关注区域模型

图3 关注区域外的超级单元模型

由于其网格数量(图2所示的模型)为114 081个，为常规分析模型的10%左右，极大提高了求解速度(本次采用常规模型分析用的时间为30 min，采用超级单元后的分析时间为157 s)。

采用超级单元计算、常规模型计算及试验测试的结果相比(见表1)，可以发现误差不大，能用来改进结构。

表1 转向系统模态结果对比 Hz

2 转向系统固有频率的快速识别

对转向系统拓扑优化分析中，需要将其固有频率作为条件进行约束，但现有商业软件中没有相应的卡片或子程序，这将制约优化工作的进行，降低优化效率，通过对频响曲线进行改进成功解决了这一问题，提升了转向系统固有频率的识别效率。以下是该方法的实现方法及过程。

当激励频率与系统固有频率一致时，响应点的振动幅值最大，理论上通过观测频响曲线的峰值即可锁定该系统的固有频率，因为固有频率对应的振型会被激励起来，若振型为第r阶，则响应点的传递函数在该频率下表现有较大的峰值。软件计算的传递函数曲线是有方向标定的，如激励点为X向，响应点为Y向，此时传递函数表达式为:

传递函数在系统固有频率处是否出现峰值，与激励点(决定φlr数值)、响应点位置(决定φkr数值)及方向选取(决定 cos α、cos β的数值)有关，因此传递函数在系统固有频率处是否出现峰值是随机的。根据概率理论之中心极限定律、大数定律可知:当选取的传递函数达到一定数量时，传递函数在系统固有频率处出现峰值的概率接近于 1。鉴于cos β的影响，在模态识别时选取针对性的激励点、在所关心的部位选取响应点，增加激励点、响应点的数量及方向，可大幅减少传递函数选取的数量。按上述原则获取的传递函数总有一个或几个在固有频率处有较大的峰值，而在其他频率处的振动幅值较小。将所有的传递函数曲线做加法运算后，合成曲线将保持固有频率处对应峰值这一特性，进而快速识别转向系统的固有频率［2－9］。

根据工程经验，在转向管柱附近选取激励点，在方向盘中心及轮边90°等分处选取响应点(如图4所示)即可较好地满足频率识别要求。根据上述原则，求解条件设置如下:在其中一个激励点处施加简谐力为F=Asin(2πft)，其中A为振幅取值为1，f为频率取1～35 Hz的所有正整数(上限选取与关注的系统固有频率范围有关)，激励方向分别为X向，求解频率为70 Hz，输出上述5个响应点在该激励力下X、Y、Z方向的速度响应，将上述设定放置在一个工况内;由于激励点为2个、激励方向分别为X、Y、Z向，需仿照前述再设置5个工况。

图4 频响曲线所需的激励点、响应点的位置示意图

将上述工况下激励点至轮心处所有的频响曲线，按等加权系数进行求和;同理求出其他响应点处的频响合成曲线(如图5所示)，并据此快速识别出转向系统在35 Hz(一般由发动机怠速工况下的激励频率确定)以内的固有频率。

以12点钟方向的频响合成曲线为例:在11.5 Hz、15 Hz、16.9 Hz、22.6 Hz、23.8 Hz、24.2 Hz、28.8 Hz、29.8 Hz、33.6 Hz的频率处曲线出现峰值，说明系统固有频率将出现在以上几个位置的概率最大。在23.8 Hz及24.2 Hz处，共有4条合成曲线出现峰值，但9点钟方向的合成曲线并未出现，说明这两个频率不是固有频率的概率较大;28.8 Hz与29.8 Hz相隔较近，两者是相近振型的可能性较大。为验证以上推测，提取上述5个响应点在各频率下的振型，相互之间做相关性计算，可以得出22.6 Hz、23.8 Hz、24.2 Hz之间的相关系数较大，最低为 0.926，23.8 Hz、24.2 Hz的相关系数为0.935，其他数据均在0.2～0.3附近。在相关性系数较大的频率中，取频响值最大点对应的频率为系统的固有频率(此时频响曲线由图5的5条曲线合成)。

图5 频响合成曲线

受车身局部模态的影响，频响合成曲线在11.5 Hz、15 Hz、16.9 Hz处存在着峰值。对图4中参考点的频响曲线(如图6所示)运用上述方法进行分析，可以得出车身在上述3个频率处存在着模态，在22.6 Hz、29.8 Hz、33.6 Hz 处不存在模态，从而判断转向系统的固有频率为22.6 Hz、29.7 Hz、33.5 Hz。

图6 参考点的频响合成曲线

3 拓扑优化分析及结构改进实现

3.1 拓扑优化分析

在第2部分分析的基础上，构建优化区域、设置求解条件进行拓扑优化分析。经设计人员确认，驾驶台前侧、前围骨架后侧、车架纵梁右侧处可以由分析人员自由修改结构来调整转向系统的固有频率。故在上述3个位置构建3个优化区域，进行拓扑优化，如图7所示。

图7 优化区域位置图

将前述响应点、参考点在频率为1～35 Hz下的速度响应作为变量，通过构建第三类响应的方式，将本文开发的快速模态识别技术通过HyperMath软件嵌入至优化分析的设置中，以此约束转向系统的固有频率大于29 Hz(怠速开空调工况下发动机的激励频率为26.7 Hz)，并约束设计空间的体积分数不高于30%，其中约束条件所依赖的工况为模态识别原理中构建频响合成曲线的6个工况，以质量最小化为目标进行优化。

从第一次拓扑优化结果(图8)可以看出，根据影响转向系统固有频率最为重要的地方在优化区域中予以保留这一原则，在工艺可行的前提下，结构工程师在此区域内展开设计，即在驾驶台立柱、驾驶台与车架、驾驶台与前围、前围弧杆间增加零件进行连接，并将此新结构用有限元软件划成网格后与设计区域中的单元用RB2连接，再次进行拓扑，第二次得到需要加强的部位，再如此一次后，即可得到调整转向系统所需的概念设计结构。

图8 拓扑优化分析结果

转向系统需要调整的的振型(仿真结果为22.6 Hz)表现为该系统沿车长方向的摆动，驾驶台立柱在车长方向的抗弯刚度为影响固有频率的主要因素。拓扑优化结果显示:可以通过增加牛腿，并在其与前围骨架、驾驶台立柱之间的区域构造封闭环结构，将车架的刚度传导至驾驶台立柱，达到提高转向系统固有频率的目的。

3.2 结构改进实现及效果

对上述新增结构的截面尺寸、厚度(客车结构主要是杆件)数据作为变量，进行尺寸优化，得到结构最终的尺寸，获取详细设计结构，改进如图9所示。

图9 拓扑优化后改进结构

结构改进后该系统的频响合成曲线如图10所示，采用上文相同的识别方法可得:第一阶固有频率已调整至29.4 Hz，达到目标要求。

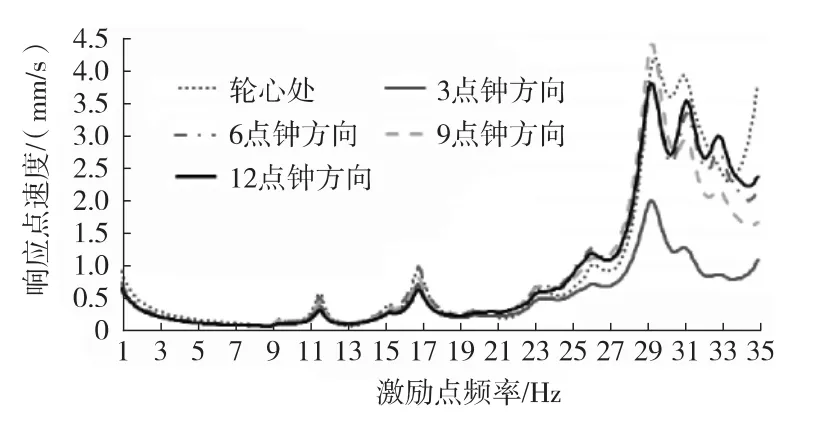
图10 结构改进后的频响合成曲线

4 结束语

采用拓扑优化技术、超级单元技术、系统模态的快速识别技术使结构改进可以顺利、快速地进行，实现了转向系统与发动机激励频率有效隔离。这种方法可以在低配置的电脑上进行，在可行的方案中逐一尝试，在设计阶段就可以避免转向系统与发动机激励频率相耦合的情况。上述方法经适当的变化，对动刚度、振动传递函数、噪声传递函数的优化亦有效。

修改稿日期:2018－07－09