电池管理系统SOC估算方法及应用

张礼宪，周雨辉，魏 涛，张景涛，陶西孟，杨继群

(中通客车控股股份有限公司，山东聊城 252000)

电池管理系统(BMS)对电动汽车的电池进行维护和管理，在保障安全性的前提下，尽可能地挖掘电池的潜能，提供更优的续驶里程和驾驶体验，是电动汽车研发的重点之一。电池荷电状态(SOC)的估算是BMS的核心功能之一，它是电动汽车电池充放电有效控制和动力性能优化管理的基础，直接影响电池的利用率和汽车的性能表现。由于SOC不能直接测量，且受众多因素的影响，所以对SOC估算方法的研究已成为电池管理系统的一项重要课题。

SOC指电池中剩余电荷的可用状态，一般用百分比表示。最常用的SOC定义为电池的剩余电量与其额定(标称)电量的百分比。在实际应用时，一般以实际最大电量代替额定(标称)电量，以考虑电池衰减、环境温度变化等因素的影响。

在电动汽车BMS行业，比较经典的SOC估算方法包括安时积分法、开路电压法以及Kalman滤波方法等，它们各有优劣。其中，安时积分法和Kalman滤波方法可以估算电池动态过程(电池充电或放电)的SOC，且估算过程中存在随时间变化的误差;开路电压法可以估算电池充分静置后，没有充放电时的SOC，且SOC的估算误差和静置时间没有关系，只与对应的SOC和电压测量误差有关。在实际应用时，往往是多种方法结合，以实现在电池系统的整个生命周期阶段都可以准确估算SOC，如在简单工况时使用安时积分法;在复杂工况时采用结合在线参数辨识的Kalman滤波方法;在OCV随SOC变化显著的区域，如果电池达到充分静置条件，再辅以开路电压校准。如此得到的SOC往往比单一方法估算的SOC更加准确。

1 安时积分法

安时积分法又称电荷累积法，是目前最常用的一种SOC估算方法［1－4］。安时积分法利用 SOC的定义，将当前的SOC写成SOC初始值与一段时间内累积流出电池的电量之差，公式如下:

式中:SOC0为SOC的初值;CN为电池容量;I为电池电流，这里约定放电电流为正，充电电流为负;η为库伦效率。

安时积分法公式简单，对于电流变化不大的工况精度较高，但是存在以下3个问题:

1)对初始值的依赖。由式(1)可以看出，如果SOC0不准确，将导致计算出的SOC一直不准确。

2)累积传感器误差。对于实际工况，电流的变化可能是剧烈的，受采样周期、采样精度的影响，电流积分值并不能完全反映真实电量的变化。这些误差又会累积到SOC中，导致对SOC的估算结果越来越差。为了消除累积传感器误差，可以在电池完全充满电或者放完电时，对累计误差进行校正，但是在电动车的实际使用过程中，这种校正条件不一定能时常达到。

3)库伦效率的影响。库伦效率η受电池温度、老化以及自放电等各种因素的影响，为了获得准确的库伦效率，需要进行大量的试验。

为了检验安时积分法的应用效果，我们使用BMS系统和德普BTS2000充放电柜对一个标称容量为60 Ah的电池包进行放电试验，放电电流为随机电流，每5 s变化一次，变化范围为0～30 A。在BMS系统中使用安时积分公式(1)对SOC进行估算，以充放电柜记录的SOC作为真实值，图1显示了SOC估算值与时间的关系。安时积分法估算，SOC有大约1.8%的初始误差(这里没有校准初始误差)，安时积分过程中SOC的初始误差不收敛。并且由于电流值受测量误差及采样周期等因素的影响，安时积分法的估算误差呈累积放大趋势，估算末期的SOC误差超过4%。

图1 安时积分法估算结果

2 开路电压法

电池充分静置(既不充电也不放电，放置至少2 h以上)后，开路电压与SOC存在一一对应的关系。开路电压法的原理是:事先通过电池测试获取SOC与OCV的对应关系(如图2所示);然后在实际使用电池时，如果电池达到了充分静置的条件，通过测量此时电池的开路电压，再反查OCV－SOC表获取其SOC 值［5］。

开路电压法的优点是实现简单、计算量小，但存在以下几个缺陷:

1)滞回电压Vh的影响。受滞回电压Vh的影响，OCV与SOC并不是精确地一一对应。OCV实际上为，其中E是电池的平衡电动势，与SOC一一对应。利用开路电压法估算SOC时，忽略了滞回电压，认为VOC等于电池的电动势，这种近似会带来一定的误差。

2)静置时间过长。为了获得准确的开路电压，需要将电池充分静置，等待电池内部的化学反应达到平衡。为了得到稳定的电压，静置时间往往长达数小时，这显然不能满足实时估算的要求。

3)存在电压平台区。特别是对磷酸铁锂电池来说，OCV－SOC关系曲线在很大范围内(SOC∈［30%，90%］)变化都非常平缓(如图2所示)。在这段范围，较小的OCV变化值对应较大的SOC变化。因此，平台区内OCV的测量误差会导致较大的SOC估算误差。试验使用BMS系统的电压测量精度是5 mV，对于图2中的磷酸铁锂电池曲线，如果测量出来的OCV比实际OCV偏大5 mV，这部分电压差导致的SOC误差如图3所示。可以看到，电压平台区的SOC估算误差甚至超过15%。

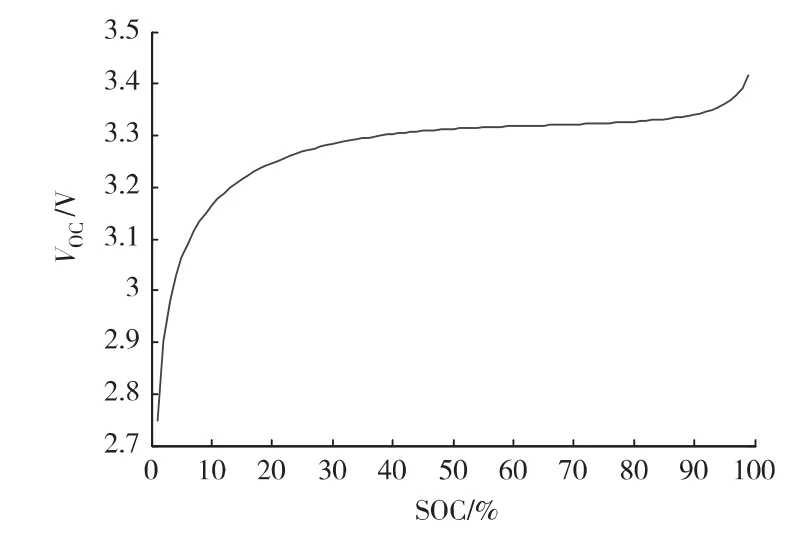
图2 磷酸铁锂电池的OCV－SOC关系曲线

图3 磷酸铁锂电池的SOC误差曲线(OCV偏大5 mV)

3 Kalman滤波法

对BMS的SOC估算问题来说，应用Kalman滤波算法，首先要建立等效电路模型［6－7］。等效电路模型的思路是用电容、电阻、电源等基本电路元器件的组合来模拟电池的动态特征。常用的等效电路模型有Rint模型、Thevenin模型、PNGV模型、Massimo Ceraolo 模型等［8－13］。

下面介绍一种较为常见的实施扩展Kalman滤波算法的思路。选用简化的Massimo Ceraolo模型，它包含1个电阻和2个RC网络，同时去掉寄生反应支路，即称为二阶RC模型，其电路结构如图4所示。这里用开路电压VOC近似代替平衡电动势E。

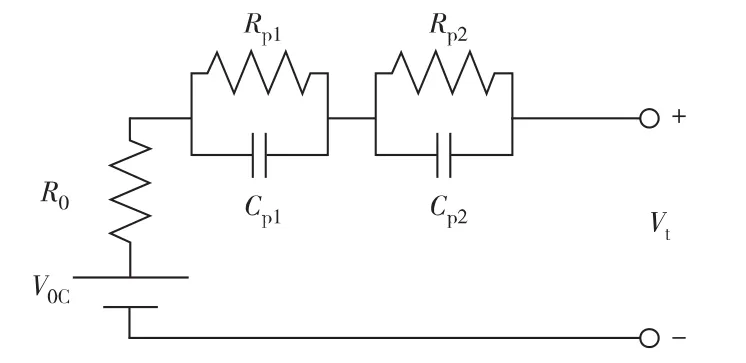
图4 二阶RC模型

约定充电电流为负，放电电流为正，该模型的状态方程如下:

量测方程如下:

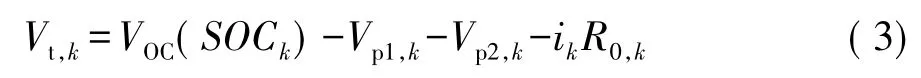
式(2)和式(3)满足扩展形式的Kalman滤波公式，可以带入扩展Kalman滤波算法执行流程，SOC作为系统状态变量之一即可以被估算出来。

使用Kalman滤波算法对SOC进行估算时，SOC初始值的系统误差会在滤波过程收敛，另外传感器的随机测量误差也可以得到抑制。但是，Kalman滤波结果的好坏依赖于参数的选取，如果未能选择合适的参数，有可能会导致滤波发散。对于参数的选取，有离线辨识和在线辨识两种方法。离线参数辨识是指事先通过试验测试的手段，确定电池模型的参数，但是由于参数会受温度、电池衰减等因素的影响，测试结果很难将这些因素涵盖全面。在线参数辨识则是指在电池系统实际运行过程中，动态地对电池模型参数进行估算，但估算参数的精度可能会较低。

本文使用Kalman滤波法估算电池包的SOC，电池模型参数由离线辨识确定，测试工况同本文“安时积分法”小节，图5和图6分别显示了其SOC估算值及SOC估算误差与时间的关系。从图6可以看到，当滤波参数选取合适时，Kalman滤波法可以很快收敛，并且在整个周期内估算误差小于2%。

图5 Kalman滤波法估算结果

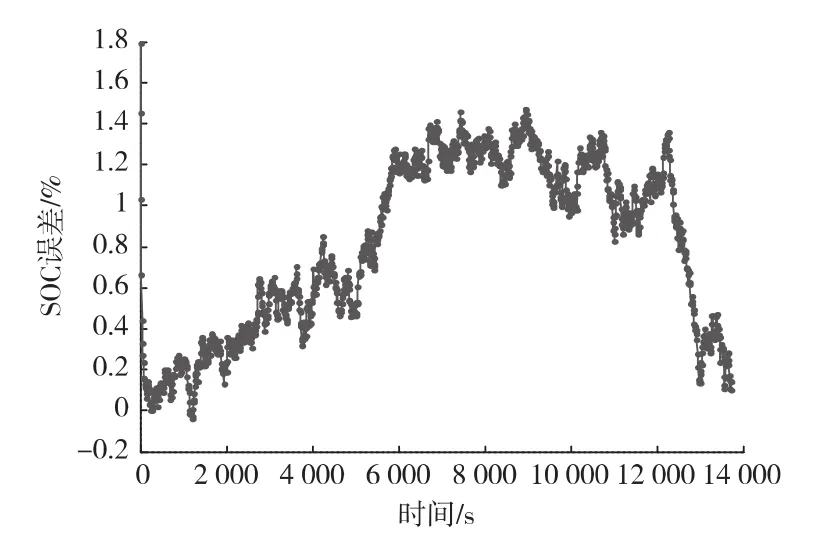
图6 Kalman滤波法估算误差

从上面的分析可知，安时积分法和开路电压法计算简单，但是受传感器精度影响较大，当BMS系统的传感器测量精度不高时，可能引起较大的SOC估算误差。Kalman滤波法可以抑制传感器的随机噪声，但是依赖于滤波参数的选取，如果参数选取不合适，可能导致滤波发散。

4 结束语

本文对目前电动汽车BMS上常用的SOC估算方法进行了综述，介绍了各方法的大致实施过程，并比较了各方法的优缺点。在实际使用时，往往是多种方法结合，综合其优势，以实现在电池系统的整个生命周期阶段，都可以得到准确的SOC估算。

修改稿日期:2018－02－25