单立柱堆垛机机架的力学分析与结构优化

黄 超，呼英俊，董颖怀

(天津科技大学机械工程学院，天津 300222)

在工业生产飞速发展的今天，仓储物流技术水平的提升势在必行．堆垛机是自动化立体仓库的重要设备，是物资流动的重要载体，提高堆垛机的存取货速度是实现自动化立体仓库高效运行的关键[1]．单立柱堆垛机作业时，机架将会受到自身重力和货物重力的作用，行走、制动和加减速的水平惯性力作用，以及起吊时冲击载荷作用，导致立柱和横梁发生弯曲、扭转变形，从而使立柱发生疲劳，产生应力集中现象，影响整机的平稳性．因此，为了保证堆垛机作业过程中的安全性与可靠性，提升堆垛机运行过程中的平稳性，对堆垛机进行动静态性能分析及结构优化具有非常重要的意义[2-3]．

近年来，国内外专家学者对堆垛机的动态特性均进行了一些具有价值的分析研究：李坚[4]构建了堆垛机的运动学模型与动力学模型，运用运动学、动力学和刚体接触动力学方法对动态特性进行分析；孙军艳等[5]利用 ADAMS软件构建堆垛机简化模型并进行动力学仿真；Randhawa等[6]对堆垛机存取车命令的执行顺序进行分析；Taboun等[7]对堆垛机位置检测进行研究．国内外对堆垛机的研究都取得了一定的进展，但我国堆垛机的结构方面还存在一定不足，在对堆垛机进行结构设计、分析与优化过程中采用的方法单一，普遍采用传统方法计算强度和刚度，操作复杂，精度较低，工作周期长，工作强度大；并且优化只针对某一不足之处，缺乏对比性，难做到最优[8]．

有限元分析方法用简单问题代替复杂问题，能够适应各种复杂形状，其计算精度高，可靠性强，实用性强，是处理复杂工程问题的重要分析手段[9]．本文结合生产实践，通过分析单立柱堆垛机功能和基本结构进行整体设计，运用有限元分析方法对机架进行静力分析与模态分析，验证模型的可行性，并进行结构优化．

1 有限元模型的建立

设定堆垛机运行的排、层和列方向分别为模型的x轴、y轴和z轴．

1.1 单立柱堆垛机结构设计

设计的单立柱堆垛机，最大起升高度 9,m，自身质量 3,512,kg，额定载荷 1,000,kg，水平运行速度5,m/s，水平运行加速度 0.3,m/s2．单立柱堆垛机的结构简图如图1所示，主要由立柱、上横梁、下横梁、载货台、水平行走机构、升降机构、货物存储机构(货叉及驱动装置)和控制柜等部分构成．

图1 单立柱堆垛机结构图Fig. 1 Structure of the single column stacker

为便于运用有限元软件ABAQUS对堆垛机进行分析计算，在利用 Solidworks软件建模时，对堆垛机模型进行了必要的简化，以缩减模型规模．堆垛机的有限元模型见图2．

图2 单立柱堆垛机有限元模型Fig. 2 Finite element model of the single column stacker

立柱顶端轮组及上横梁质量较小，主要作用是防止机身在 x轴方向倾倒，在建模时舍去该部分，并在有限元分析时施加x方向的等效约束；载货台简化为矩形框，分为上下两处与立柱相结合，以符合工作实际；立柱、下横梁均为厚度 0.01,m 的箱形结构；提升机构简化为质量块，与立柱结合；电气控制机柜简化为质量块，与下横梁结合；下横梁两端的轮组主要起水平导向和支撑作用，在此简化为 2个质量块；其余细小且不易引起应力集中的结构(如倒角)在建模时均进行了简化．

1.2 定义材料和网格划分

材料属性与几何模型不同，代表着材料本身具有的属性，比如强度、密度、硬度等．本文对堆垛机进行单元分析计算时需要设置材料属性，根据堆垛机自身性能和实际需要，选取 Q235A作为机身材料，其属性参数为：密度 7,800,kg/m3，弹性模量 2.1×1011,Pa，泊松比0.26．

运用有限元软件对模型进行计算分析时，布尔运算容易导致出现错误，因此在建模时将模型生成一个整体[10]．在ABAQUS中先将模型分割成5个质量单元，再分别布种子、划分网格．单元形状选择六面体，单元类型为C3D8R，采用结构化网格划分技术，最终划分的有限元网格单元总数约为13,000．

1.3 约束和加载

由工程实际分析得出，载货台位于最高位满载且堆垛机沿z轴负向以0.3,m/s2的最大水平加速度瞬时启动时，机架尤其是立柱受到的冲击最大，此时堆垛机处于最危险的状态．运用极限法，将上述瞬时运动状态转化为静止状态进行研究．

施加约束时，选择对模型影响较小的节点或面进行施加，以避免过约束引起不合实际的应力集中影响计算结果的准确性．结合堆垛机的工作实际，约束和加载图见图 3．图 3中，为防止机身倾倒，在立柱顶端上横梁行走轮的等效位置选取两个点，约束该两个点在x方向的自由度；对下横梁行走轮质量块的底面施加全位移约束．

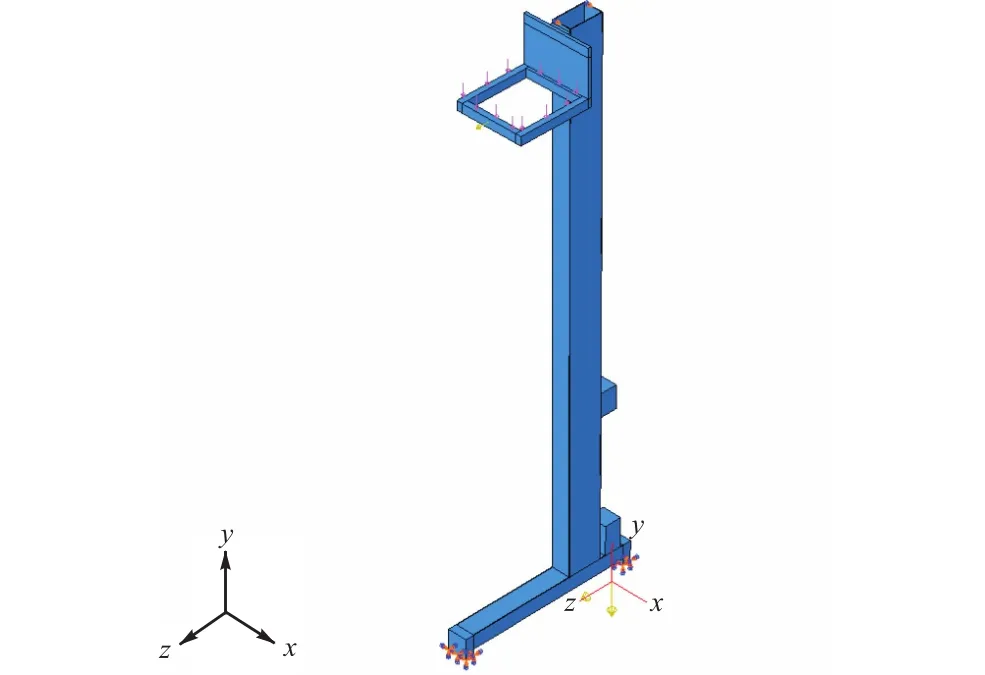
图3 堆垛机约束和加载图Fig. 3 Constraint and loading of the stacker

通过对机身施加沿y轴负向、大小为9.8,m/s2的重力加速度，实现机身重力加载；通过对机身施加 z轴方向、大小为 0.3,m/s2的水平加速度，实现其自身惯性力的加载；货物的重力以压强的形式施加到矩形框的上表面；启动时货物产生沿z轴方向的惯性力作用于机身，因此，在矩形框等效位置施加 z轴方向集中力 F(F＝m货a＝300,N)．同时，对堆垛机机架强度、刚度影响不大的细小构件忽略不计．

2 静力分析

通过 ABAQUS运行计算，得到堆垛机的变形云图如图4所示，应力云图如图5所示．

由图 4可知，在最大动载荷作用下，立柱顶端的挠度为 9.666×10–3,m．根据经验公式[13]，堆垛机立柱的许用挠度为[f]＝H/2,000～H/1,000＝4.5～9,mm，堆垛机立柱不满足刚度要求，需进行优化．

由图5可知，堆垛机机架的最大应力出现在载货台与立柱的下方结合部位，为 6.088×107,Pa的压应力．此外，立柱根部与下横梁结合处的压应力接近4×107,Pa．Q235A 材料的屈服强度 δs＝2.35×108,Pa，选择安全系数[s]＝2，材料的许用应力[δ]＝δs/[s]＝1.175×108,Pa．最大应力小于材料的许用应力，满足强度要求．

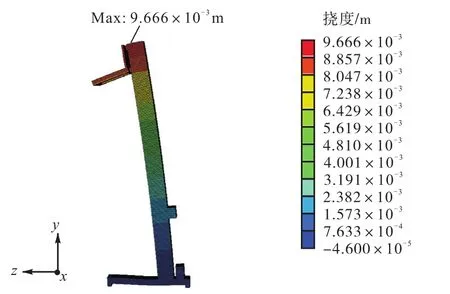
图4 堆垛机变形云图Fig. 4 Deformation nephogram of the stacker

图5 堆垛机应力云图Fig. 5 Stress nephogram of the stacker

3 模态分析

堆垛机结构的动态特性是影响堆垛机定位精度、稳定性的重要因素[11]，可以通过模态分析解决堆垛机稳定性差的问题．运用 ABAQUS有限元软件对堆垛机模型进行模态分析，不仅可以得到其固有频率，还可以获得机架在相应振动频率下的振型特征，有助于清楚认识机架对不同类型的动载荷如何响应[12]．

高阶频率对堆垛机结构的动力性影响较小，所以在ABAQUS分析时只提取前6阶频率．通过分析计算得到工况载荷下前6阶固有频率及前6阶振型，如图 6所示．从图 6可以看出：第一阶振型以立柱沿 z轴的弯曲变形为主；第二阶振型以立柱在xoz平面内的扭曲变形为主；第三阶振型以立柱沿x轴负向的弯曲变形为主，并且载货台框架有扭曲变形；第四阶振型是载货台沿 y轴方向的弯曲变形和立柱沿 z轴负向的弯曲变形为主；第五阶和第六阶振型，整个机架发生了较复杂的弯曲扭转变形．

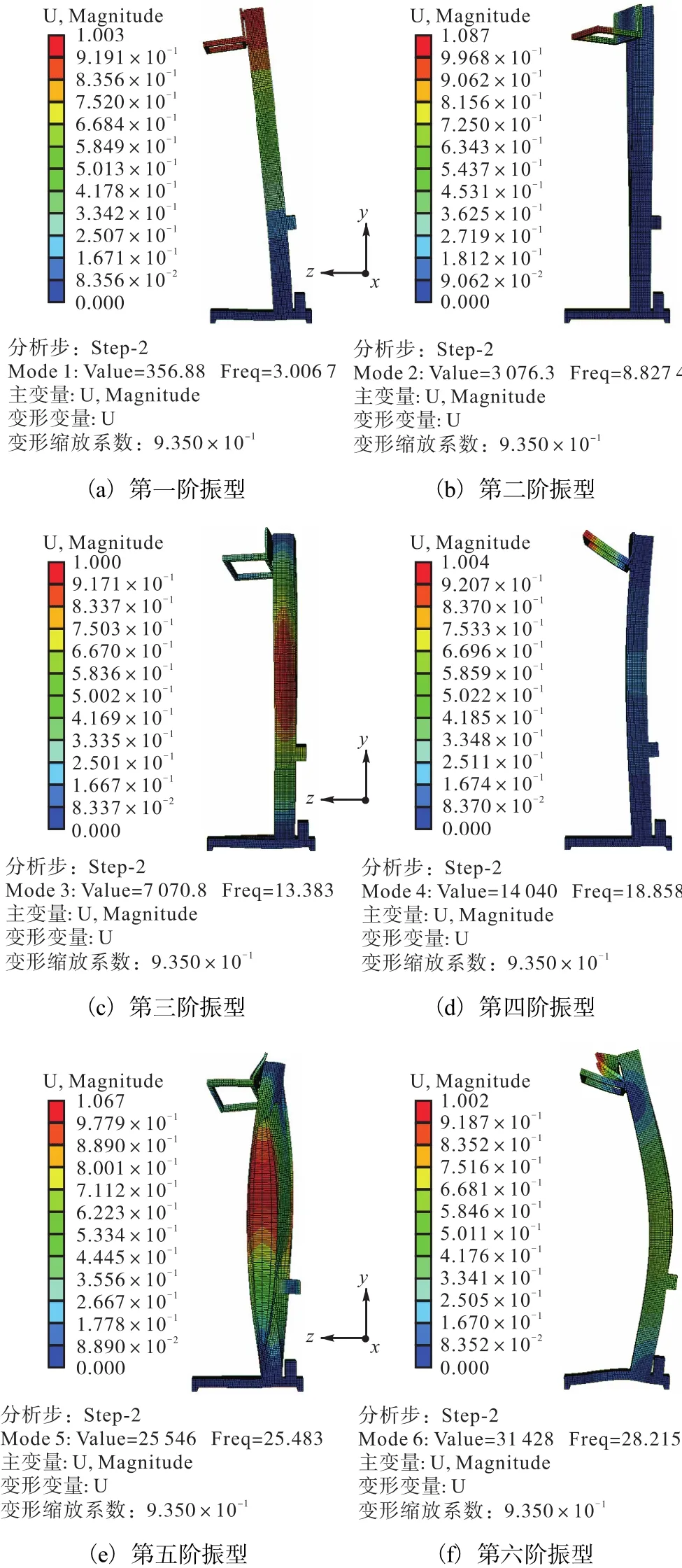
图6 单立柱堆垛机前6阶模态振型图Fig. 6 The mode shapes of the first six orders of the single column stacker

结构设计时，应该注意避免共振现象的发生．立体仓库堆垛机水平行走的地轨不是一段完整的钢轨，虽然在铺设时对焊接工艺要求高，使其尽可能平滑，但焊缝仍对行走轮产生激励[14]．本文设计中堆垛机两行走轮的轴心距为 3.3,m，若堆垛机以 5,m/s的速度水平运行，受到的激励频率为 1.515,Hz，小于堆垛机的第一阶频率3.006,7,Hz．堆垛机运行安全．

4 堆垛机立柱的结构优化

工况载荷下，堆垛机受力情况较为复杂，尤其是立柱作为堆垛机的核心机构，受到的冲击最大．由上述静力分析结果得出，堆垛机的强度满足设计要求，但立柱顶端的挠度较大，不满足刚度设计要求．因此，需要对堆垛机的立柱结构进行优化．

4.1 结构优化方案

堆垛机立柱由厚度 0.01,m的钢板焊接而成，且立柱的弯曲变形主要是沿z轴方向发生的，因此确定改进思路为：在不改变钢板厚度和立柱高度的前提下，通过增大立柱箱形横向截面沿z轴方向的有效尺寸，增强立柱的抗弯能力，从而减小立柱顶端挠度．立柱在yoz面的纵向截面示意图见图7．

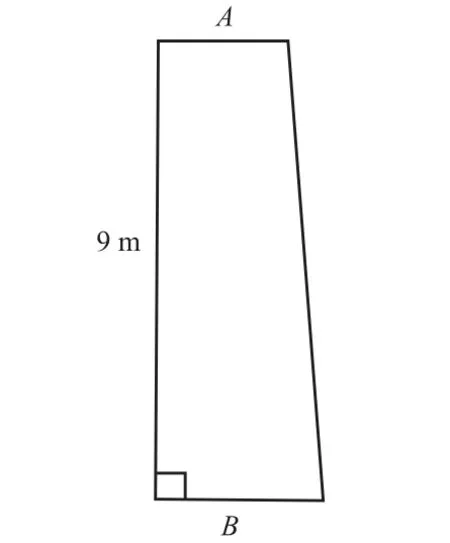
图7 yoz面内的立柱截面图Fig. 7 Vertical section diagram of the column on yoz surface

立柱高度为 9,m，设截面上底、下底长度分别为A、B．初始方案中，A＝B＝0.60,m；优化过程中，通过参数化建模，以A、B长度为优化对象，以减小立柱顶端挠度为优化目标，结合机身总质量和所受最大应力两项指标，提出3种优化方案．

方案 1：A、B 均增大，分别同时取 0.61、0.62、0.63、0.64、0.65,m，重新建模后的有限元静力分析结果见表1．

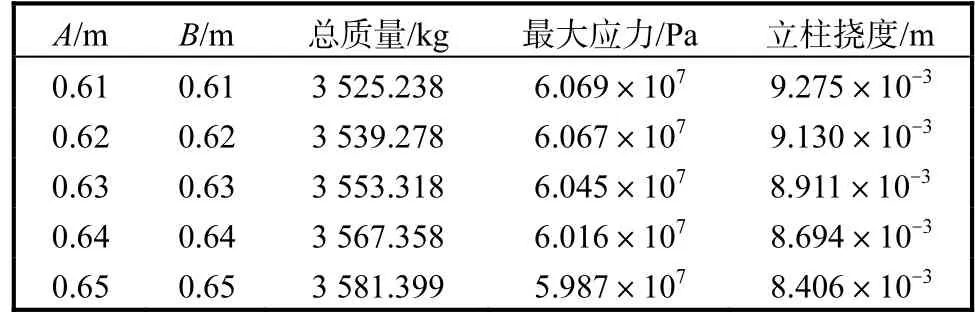
表1 方案1分析结果Tab. 1 Analysis results of scheme 1

与初始方案比较，方案1中，随着A、B长度的逐渐增大，机身质量逐渐增加，最大应力逐渐减小，立柱挠度也呈减小趋势，从第 3组数据 A、B同时增加到 0.63,m 开始，立柱挠度减小到许用挠度值 9×10-3,m以下，立柱刚度满足要求．

方案 2：A不变，为 0.6,m，B增大，分别取 0.62、0.64、0.66、0.68、0.70,m，重新建模后的有限元静力分析结果见表2．

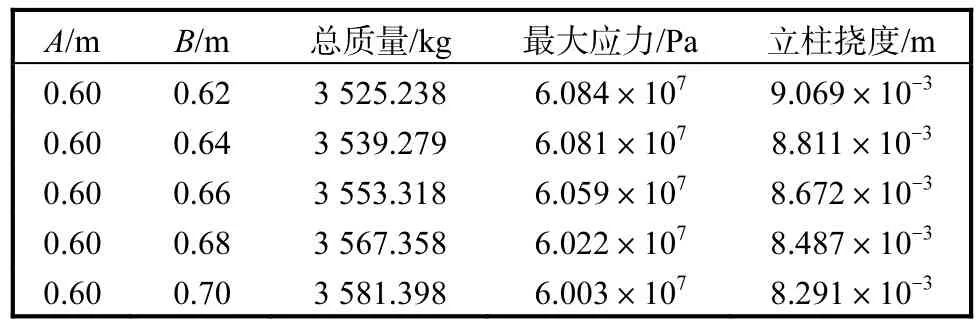
表2 方案2分析结果Tab. 2 Analysis results of scheme 2

与初始方案比较，方案2中，随着B长度的逐渐增大，机身质量逐渐增加，立柱的最大应力呈减小趋势，立柱挠度也逐渐减小，从B增加到0.64,m开始，立柱挠度减小到许用挠度 9×10-3,m以下，立柱刚度满足要求．

方案3：A减小，B增大，A和B分别取0.58,m和0.64,m、0.56,m 和 0.68,m、0.54,m 和 0.72,m、0.52,m和0.76,m、0.50,m和0.80,m，重新建模后的有限元静力分析结果见表3．

表3 方案3分析结果Tab. 3 Analysis results of scheme 3

与初始方案比较，方案3中，随着A长度的减小和 B长度的增大，机身质量逐渐增加，立柱的最大应力呈增大趋势，立柱挠度呈减小趋势，在 5组数据中，立柱挠度均在许用挠度 9×10-3,m 以下，满足刚度要求．

4.2 结构优化分析

3种优化方案均对减小立柱挠度有效果，可以使立柱刚度满足要求．对比后发现：在堆垛机总质量增加相近的情况下，方案 3中立柱挠度的减小情况最好，其次是方案2，最后是方案1．例如选取3种方案的第4组数据：方案1、方案2、方案3中堆垛机总质量均约为 3,567,kg，质量增幅 1.57%,，立柱挠度值依次为 8.694×10-3,m、8.487×10-3,m、7.971×10-3,m，挠度降幅依次为 10.06%,、12.20%,、17.56%,，虽然方案 3中立柱的最大应力比改进前略微增大，但是增幅仅为1.85%,，且远小于材料的许用应力．由此可得，针对挠度值的优化方案中，方案3的效果更明显．

方案 3中各组模型立柱的挠度均减小到了许用值以下，综合考虑 5组数据中机身质量、最大应力的变化幅度以及立柱挠度的优化效果，最终选定优化方案：立柱高度和壁厚保持不变，纵向截面上底减小为0.56,m，下底增大为 0.68,m．较初始方案，机身增重0.8%,，最大应力 6.156×107,Pa，增大 1.1%,，特别是立柱挠度 8.561×10-3,m，减小 11.4%,，满足刚度设计要求．经模态分析，此优化模型的第一阶固有频率为3.660,8,Hz，大于所受到1.515,Hz的激励频率．因此，优化结果满足设计要求，效果明显．

5 结 语

运用ABAQUS有限元软件对所设计的单立柱堆垛机进行动静态分析，发现在最大动载荷作用下，该机型的强度符合设计要求，以最大水平速度运行时，满足振动要求，但立柱的顶端挠度值大于规定的允许挠度值，不符合刚度要求．

以增大箱形横截面沿立柱弯曲方向的有效高度为思路，提出了 3种结构优化方案．通过参数化建模和静力分析可知，3种优化方案对立柱挠度的减小均有效果，都可以使立柱刚度满足设计要求．进一步对比得出：在机身自重相近的情况下，减小立柱纵向截面上底，增大纵向截面下底，此时立柱顶端的挠度减小幅度最大，优化效果最显著．