基于谓词的Paillier型密文解密外包方案

张 薇， 白 平， 李镇林， 李 聪

(1.武警工程大学 密码工程学院 陕西 西安 710086； 2.武警工程大学 信息安全保密重点实验室 陕西 西安 710086)

0 引言

随着云计算技术(cloud computing)[1]的快速发展和逐步完善，越来越多的用户倾向于将复杂的计算资源、存储资源外包给“云端”，从而极大地减轻了用户的负担.然而 “云端”并不是完全可信的，人们在享受“云端”所带来便利的同时，对于数据的访问控制也进行了各种尝试，从不同角度对数据访问控制权限进行研究[2-4].然而，将同态加密与谓词相联系的研究却很少.试想如果用户将明文数据直接交由“云端”处理，无疑会增加数据的安全隐患.为了防止“云端”的恶意篡改和非法用户访问敏感数据，用户不仅需要对敏感数据进行加密，更重要的是要设置必要的访问控制策略.在传统的云计算加解密模型中，无法实现对计算结果的访问控制.在公钥密码体制中，用户的身份是由数字证书来确认的，但证书的使用无疑会增加系统的开销，这将无法体现出云的优势.文献[5]提出了谓词加密(predicate encryption，PE)，因其能够实现对密文更加精细、灵活的访问控制而备受关注.

方案以类同态Paillier方案[11]为基础，结合经典文献[12]提出的KP-ABE(key-policy ABE)型密文解密外包设计思想，构造了一个基于谓词的Paillier型密文解密外包方案.相比文献[12]，该方案在解密时间上有所增长，但是对密文的访问控制却优于文献[12]，增强了用户数据的安全性，从而在一定程度上减小了数据泄露的概率，方案还可以抵抗任何恶意云服务器的攻击.在方案构造中，部分密文的解密被外包到云上进行，减小了用户的计算量，更为重要的是对密文的访问控制策略被隐藏在密文当中，所以要想完成对密文的正常解密，要求用户属性必须满足密文策略，实现了用户对外包计算结果的有效控制.此外，方案对密文可以进行任意次加法同态操作和一次乘法同态操作.同态加密可以允许用户在不知道明文的情况下对密文进行操作，从而很大程度上方便了用户.随着同态加密受到越来越多的关注，涌现出了许多同态加密的研究成果[13-14].

1 预备知识

1.1 双线性映射

G，GT是两个阶为p的循环群，g为生成元，则双线性映射[15]e:G×G→GT满足下列性质：

1) 双线性.对任意r,s∈G和a,b∈Zp，都有e(ra,sb)=e(r,s)ab.

2) 非退化性.存在r,s∈G，使得e(r,s)≠1.

3) 可计算性.存在有效的多项式算法对任意r,s∈GT，都可以计算出e(r,s).

1.2 访问结构

定义P={P1,P2,…,Pn}是秘密共享的参与者集合.访问结构AS是2p上的一个非空子集，即AS⊆2p{∅}.访问结构单调性定义如下：∀A,B，如果A∈AS且A⊆B，则B∈AS.同时，对于能重构出共享秘密的子集称为授权集合；反之，则称为非授权集合.

1.3 LSSS矩阵访问结构

定义在秘密共享参与者集合P上的线性秘密共享机制[15](linear secret sharing scheme，LSSS)是指：

1) 所有参与者的共享组成一个Zp上的向量.

2) 存在一个l×n的矩阵M，它是一个关于的共享生成矩阵.M的第i行标记成ρ(i)，其中i=1,2,…,l，ρ是从{1,2,…,l}到P的映射函数.随机选择列向量其中s是共享秘密，那么M·v就是利用得到的关于s的l个共享组成的向量，并且(M·v)i对应于ρ(i).

1.4 Paillier方案

Paillier公钥密码[11]是由Paillier在1999年提出的一种基于高次剩余类问题的加密体制，该体制具有同态的优良性质，其良好的同态性质可以用于构造很多实用且高效的密码算法.方案的具体描述如下：

解密算法.解密者收到密文c后，使用私钥sk可计算出明文m=L(cnmodn2)·φmodn.具体解密过程为

Paillier方案同态性质分析.

1) 加法同态：

2) 乘法同态：

1.5 安全模型

方案的安全模型引用文献[6].

初始化运用算法Γ生成公钥参数，将其传送给敌手B.

步骤1敌手B对多组谓词向量v对应的密钥skv进行询问.

博弈敌手B输出长度相同的明文消息m0和m1及其相应的属性x0和x1.假如步骤1中的谓词向量v不满足条件fv(x0)=1,fv(x1)=1，则挑战者C用属性xb随机加密明文mb，其中b∈{0,1}.然后将对应的加密密文c*发送给敌手B.

步骤2敌手B按照步骤1的方式不断询问直到谓词向量v满足条件fv(x0)=1,fv(x1)=1.

猜想敌手B输出b′，如果b′=b，则攻击成功.

定义1当敌手B在上述交互过程中的优势是可以忽略的，方案是IND-AH-CPA安全的.

Payload-hiding安全只能保护明文信息不被窃取，对于其他相关信息是做不到隐私保护的.这在一些保密要求高的应用场合(如属性信息也要求保密)是不适用的.该方案可以达到attribute-hiding安全：可以将明文信息和属性信息同时混淆在加密密文中而不被泄露.相比而言，attribute-hiding在安全性和适用范围上要比payload-hiding有更广泛前景.

1.6 安全假设

方案的安全性假设借鉴了文献[16]中基于双线性映射子群判定问题的扩展.

输入生成元g和安全参数1λ，输出元组(N=p1p2p3,G,GT,e)，其中p1,p2,p3是互不相同的素数.G和GT均是阶为N的循环群，定义Gp1,Gp2,Gp3是G的子群.随机选择生成元q∈Gp1.为了便于说明，引入一个参数h∈Gp1，由于参数h对于挑战者来说是独立的，故参数h的引入并不会增加敌手的优势.

假设1根据生成元g定义：

(N=p1p2p3,G,GT,e)←g，

q,h←Gp1,X3←Gp3,

D=(G,q,h,X3),

T0←Gp1,T1←Gp1p2.

定义算法Λ能够区分某一元素属于Gp1或者Gp1p2的优势为

Adv1g,Λ(λ)=|Pr[Λ(D,T0)=0]-Pr[Λ(D,T1)=0]|.

定义2对于多项式时间算法Λ，当Adv1g,Λ(λ)可忽略时，则满足假设1.

假设2根据生成元g定义：

(N=p1p2p3,G,GT,e)←G,

q,h，X1←Gp1,X2,Y2←Gp2,X3，Y3←Gp3,

D=(G,q,h,X3,X1X2,Y2Y3),

T0=Gp1p3,T1←Gp1p2p3.

定义算法Λ能够区分某一元素属于Gp1p3或者Gp1p2p3的优势为

Adv2g,Λ(λ)=|Pr[Λ(D,T0)=0]-Pr[Λ(D,T1)=0]|.

定义3对于多项式时间算法Λ，当Adv2g,Λ(λ)可忽略时，则满足假设2.

假设3根据生成元g定义：

(N=p1p2p3,G,GT,e)←g,k∈ZN,

q,h←Gp1,X2,Y2,Z2←Gp2,X3←Gp3,

D=(G,X3,Z2,q,qkX2,hY2),

T0=e(q,h)k,T1←GT.

定义算法Λ能够区分某一元素是T0还是属于GT的优势为

Adv3g,Λ(λ)=|Pr[Λ(D,T0)=0]-Pr[Λ(D,T1)=0]|.

定义4对于多项式时间算法Λ，当Adv3g,Λ(λ)可忽略时，则满足假设3.

2 基于谓词的Paillier型密文解密外包系统模型

在阐述方案构造之前，首先简要介绍有关基于谓词的密文解密外包主要部分的工作流程模式.该方案主要涉及“云端”和用户两个主体.它们之间的交互过程可以分为两步进行.第一步，用户给 “云端”发送一个转换密钥TK，主要作用是将外包给 “云端”的密文进行必要的转换以方便用户的解密操作.第二步，“云端”利用用户发送的转换密钥TK，将存储在自己服务器上的密文进行相应的转换，以满足用户需求，而后将其回传给用户.

1) “云端”:具有较强的计算和存储能力，可以为用户提供更为方便快捷的服务，但是云服务器是属于完全不可信或者半可信的.所以必须对敏感数据进行加密，并且设定必要的访问控制权限.

2) 用户:具有较弱的计算和存储能力，倾向于把一些复杂的数据资源交给“云端”来处理，但希望这些数据不能被云服务器窃取或者篡改.

3 基于谓词的Paillier型密文解密外包方案

本小节主要介绍该方案的具体实现过程，通过将Paillier方案与密文解密外包思想相结合，构造了基于谓词的Paillier型密文解密外包方案，可以实现对云计算结果的访问控制.方案主要由以下5个算法构成.

PK={g,g1=ga,e(g,g)α,{Ti=gti}i=1,…,n,F}，

主密钥MK=(gα,PK).

(1)

最终是密文形式

C=(c,c1).

(2)

PK,K=K′1/ε=g-xi/sεgat/r,L=L′1/ε=g(t′/ε)=gt,

私钥为SK=(ε,TK,skv).

转换算法(TK,CT).输入转换密钥TK=(PK,K,L,{Kx}x∈S)和密文CT=(C,C′,C1,…,Cl)，如果属性S不满足访问结构(M,ρ)，则输出⊥；反之定义I={i:ρ(i)∈S}，且I⊆{1,2,…,l},存在常数集{ωi∈Zp}i∈I,对于{λi}中所有的值，∑i∈Iωiλi=s.运用转换算法计算.

(3)

算法最后输出部分密文CT′=(C,Q).

解密算法(SK,CT).输入私钥SK=(ε,TK,skv)和密文CT，假如密文CT不是部分密文，则需要先运行转换算法(TK,CT)，将其转换为部分密文.转换算法(TK,CT)输出为⊥时，则解密算法也输出⊥.反之，利用(ε,Q)计算出Qε=e(g,g)rxi，再利用解密密钥skv，结合Euler函数计算

L(cηmodn2)·φ·H(e(c1,di))=L((1+n)m/H(e(g,g)-rxi)·Rn)ηmodn2·η-1·

(m/H(e(g,g)-rxi))·H(e(g,g)-rxi·e(g,h)sr∑xivi).

(4)

只有当接收方的谓词向量满足x·v=0 modN，才可恢复出明文消息.根据哈希函数的抗碰撞性质，如果非法解密者不能满足x·v=0 modN，则无法计算获得明文.

4 方案分析

4.1 安全性分析

本方案在子群判定问题困难假设下达到了语义安全.同时，需要注意的是，密文属性的泄露不会影响密文的安全.因为即使攻击者拿到密文的属性向量x，即攻击者能够算出e(g,g)-rxi的值，但是攻击者得不到谓词向量v的值，无法满足fv(x)=1，从而不能正确解密得到明文m.另一方面，攻击者即使同时拿到了属性向量x和谓词向量v，满足fv(x)=1.但攻击者如果得不到随机参数ε，攻击者也不能正常解密而得到明文m.综上所述，只有当攻击者得到谓词密钥才能解密嵌套了属性向量x的密文，同时得到随机参数ε从而获得访问控制权限，才能真正攻击成功.

为了证明该方案的安全性，采用文献[16]的方法.证明先前定义的两种结构.

正常密钥能够解密正常密文和半功能密文，同时正常密文可以由正常密钥和半功能密钥解密.当使用半功能密钥解密半功能密文时，结果的等式中多出e(g2,g2)cd∑yi·zi.只有满足∑yi·zi=0时，半功能密钥才能够解密半功能密文.

基于以上分析，可以通过证明以下Game[15]的不可区分性而达到证明该方案的安全性.

Game0中密文为半功能密文，密钥均为正常密钥.

Gamereal实际加密环境过程中使用的均为正常密文和正常密钥.

Gamek中前k次对半功能密钥查询，大于k次的均是对正常密钥查询.

Gamefinal中密文为半功能密文，而密钥为半功能密钥.

证明敌手B将(G,q,h,X3,T)作为算法初始化输入，随机选择a∈ZN,ti∈ZN,i=1,…,n.公共参数和算法初始化公开参数相同.敌手B模拟Gamereal，Game0与敌手A进行交互.

使用谓词向量v,敌手B能够通过主密钥MK生成相应的正常解密密钥.

敌手A选择等长的明文(m0,m1)及相应的属性(x0,x1)，敌手B将假设1嵌入到挑战密文中，而后使用掷硬币的方式进行加密，生成密文形式为

证明敌手B将(q,h,X3,T,Y2Y3,X1X2)作为算法的输入，随机选择a∈ZN,ti∈ZN,i=1,…,n.公共参数和引理1中公开参数相同.敌手B模拟Gamek-1，Gamek与敌手A进行交互.

使用谓词向量v,当敌手B在查询次数大于k的情况下，能够利用MK生成正常解密密钥，而在查询次数小于k的情况下，则生成半功能密钥.随机选择s,d∈ZN，生成的半功能解密密钥表示为

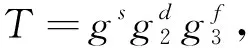
敌手A选择等长的明文(m0,m1)及相应的属性(x0,x1)，敌手B通过使用掷硬币的方式进行随机加密，密文形式为

证明敌手B将(q,X3,Z2,grX2,hY2,T)作为输入，随机选择a∈ZN,ti∈ZN,i=1,…,n.公共参数为PK={g,hY2,g1=ga,{Ti=gti}i=1,…,n}.参数N的分解不被A所获知，故A无法正确区分hY2和h.敌手B模拟Gameq，Gamefinal与敌手A进行交互.

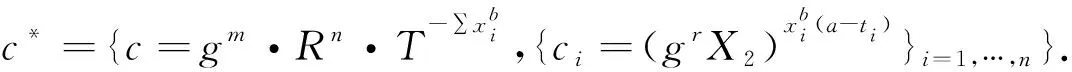
如果T=gm/H(e(g,h)r)-m，则上述密文c*为半功能密文；如果T∈GT，则上述密文c*为随机明文的加密的半功能密文，因此能够模拟Gamefinal,故B能够利用A的输出以优势ε解决假设3.

定理1如果上述的3个假设均为困难问题，则该方案为IND-AH-CPA安全.

证明如果上述的假设为困难问题，则由以上的分析可知Gamefinal与实际加密环境是不可区分的.在Gamefinal中挑战密文是不会泄漏关于B的任何信息.故敌手A攻击该该方案成功的概率几乎可以忽略不计，方案可达到IND-AH-CPA安全.

4.2 性能分析

本方案相比于文献[12]中Green的方案，改进之处是能够支持对外包密文的同态操作，更重要的是方案的安全性并不完全取决于属性参数，属性参数的泄露并不会对密文造成致命的影响.这意味着即使敌手获得了相关属性参数而没有掌握用户事先随机设定的参数时，敌手仍然是无法攻击成功的，从而在很大程度上增强了用户数据的安全性.

Green等人在文献[12]中提出了基于属性的密文解密外包思想，并构造了一个密文策略外包方案.为了更好地展示方案的优缺点，我们将在完全密文长度、完全密文解密时间、部分密文长度和部分解密时间分别与文献[12]和文献[17]进行比较.表1中l表示线性秘密共享机制LSSS中l×n矩阵中的行数，k表示密文序列长度.P、EG分别表示在G中计算线性最大时间和求模幂运算的最大时间，ET表示在GT中计算模的最大时间，在计算时间中忽略了起非主导作用操作所消耗的时间.通过分析表1可以得出如下结论：本方案在全密文长度和外包解密时间上比Green方案略长.然而，方案在访问控制上却可以优于Green方案，安全性不仅仅取决于单一的属性变量，提高了用户数据的安全性，从而达IND-AH-CPA安全.具体的比较结果如表1所示.

表1 效率分析比较

4.3 同态性质分析

1) 加法同态

g(m1+m2)/H(e(g,g)-rxi)(R1R2)n=E(m1+m2,PK).

如果解密者想要求出式中e(g,g)-rxi的值，则属性必须满足密文策略，而后通过解密算法求出m1+m2,

E(m1,PK)gm2=gm1e(g,g)-rxiRn1gm2modn2=E(m1+m2,PK).

2) 乘法同态

与加法同态类似，只有满足密文策略的解密者才能正确解密.

5 结束语

本文通过将谓词向量引入到类同态Parllier方案中，构造了一个适用于云计算环境的外包方案.方案通过将谓词向量隐藏在密文中的举措，有效地解决了用户对云计算结果的访问控制问题，而且外包过程中将复杂的计算任务交由云服务器来完成，很大程度上减轻了用户的开销，提高了外包密文的解密效率.需要更进一步的工作是探索密文解密外包与全同态加密方案的有机结合，构造一个云环境下访问控制性能更好的全同态密文解密外包方案.