基于干扰观测的制导控制一体化反演滑模研究*

王志凯，马建伟，宋晓娜

（河南科技大学信息工程学院，河南 洛阳 471023）

0 引言

传统的制导与控制系统的设计，是基于频谱分离的思想，把系统分为快回路（控制回路）与慢回路（制导回路）。首先设计制导回路，获得期望过载；然后设计自动驾驶仪控制回路，对期望的过载进行跟踪，最后把控制回路嵌入到制导回路中进行联调。末制导阶段时，随着导弹与目标距离的接近，制导回路频率变快，两回路间的耦合变大，分开设计两回路时控制难度大，易导致较大的脱靶量。IGC方法［1-3］的思想是不区分制导回路与控制回路，将其作为一个整体考虑，充分考虑制导与控制回路的耦合关系，根据通过弹-目相对运动关系，利用视线角与导弹姿态信息直接产生舵偏角指令。这样既能保证避免出现导弹失稳现象，又能提高制导精度。

自20世纪80年代威廉姆斯等人提出导弹制导控制一体化概念以来，国内外很多学者对此做了大量的研究。Idan M等人［4-5］将零脱靶量作为滑模面，采用滑模方法设计了IGC控制器。董朝阳等［6］采用扩张状态观测器对系统不确定性和干扰进行估计和补偿。采用反步终端滑模实现姿态控制。孙向宇等［7］在模型中引入不确定性，采用连续非光滑控制对三维块系统设计观测器进行补偿，结合块动态逆法与反步法设计控制器。M Sharma等［8］人使用神经网络、自适应等方法，对模型的误差及不确定性进行在线估计，并利用反步法设计了IGC控制器。虽然对一体化控制技术已经有了很多的研究方法，但仍存在许多问题亟待解决。

本文针对俯仰通道IGC模型，将模型的不确定性及参数摄动等因素视为干扰，通过NDO对其进行估计，通过补偿来削弱不确定扰动带来的影响。结合反演滑模与动态面法设计IGC控制器，为了削弱滑模控制带来的抖振，采用了自适应趋近律方法。通过Lyapunov理论证明了系统的稳定性。仿真结果表明，所设计的一体化控制器可以取得较小的脱靶量，系统对干扰及不确定性具有较强的鲁棒性。

1 制导控制一体化建模

1.1 弹-目相对运动关系

图1 纵向平面弹-目相对运动关系

图1中M和T分别为导弹与目标的位置，Vm和Vt分别为导弹与目标的速度，θm和θt分别为导弹与目标的弹道倾角，am和at分别为导弹与目标的切向加速度，q为弹目视线角，R为弹-目之间的相对距离。定义角q与角θ在基准线之上的角度为正，反之为负。

由图1所示的弹-目运动关系，根据牛顿力学定理，可得出导弹在纵向平面内的相对运动关系方程为：

式中，Vq为视线角速率即垂直于视线方向的弹目相对速度。

对式（2）求导并将式（1）带入可得

对式（3）求导，并将式（4）带入可得

式（5）中的Δq未知有界不确定项，假设导弹的运动过程，导弹的运动速度不发生变化，只改变速度的方向。

1.2 导弹制导控制一体化动力学建模

为了便于对问题的分析，对导弹的运动学建模作出以下假设：

假设1：由于一体化控制主要用于末制导阶段，认为导弹发动机推力为零，导弹速度不变。

假设4：把其他通道对纵向通道的耦合作用，认为是未知有界不确定扰动。

基于上述假设，本文采用如下动力学模型［9］。

式（6）～ 式（9）中，α 为导弹的攻角；ωz为俯仰角速率；m为导弹质量，v为导弹速度；q为动压；S为导弹特征面积；L为导弹气动弦长；Iz为导弹对z轴的转动惯量；δz为导弹舵偏角；ϑ为俯仰角；θ为弹道倾角为导弹攻角α对应的升力系数；和分别为ωz、α和δz对应的俯仰力矩系数。

根据导弹动力学关系，由式（6）、式（8）、式（9）可得导弹的加速度为：

根据以上分析，综合式（10）可得导弹制导控制一体化模型如下：

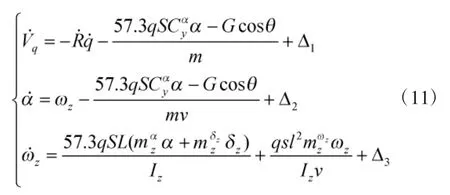
制导控制一体化模型可以写成如下形式：

系统的状态变量及输入变量如下：

式中：

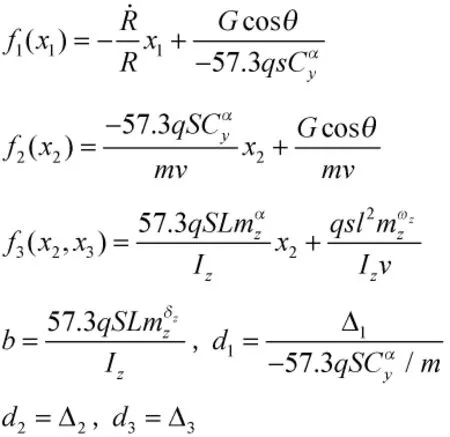
2 非线性干扰观测器（NDO）设计

为了消除未建模误差，参数摄动等不确定性系统的影响，本文将其视为未知扰动，采用非线性扰动观测器来估计未知干扰。以式（12）的第1式为例，说明干扰观测器的设计原理。

系统方程为：

本文设计如下形式的干扰观测器［10］

现定义观测器误差：

一般情况下关于干扰d的微分先验知识是未知的，假设干扰d的变化，相对于观测器的动态特性的变化是缓慢的，即认为=0。现考虑式（14）、式（16），可以得到观测器误差动态方程为：

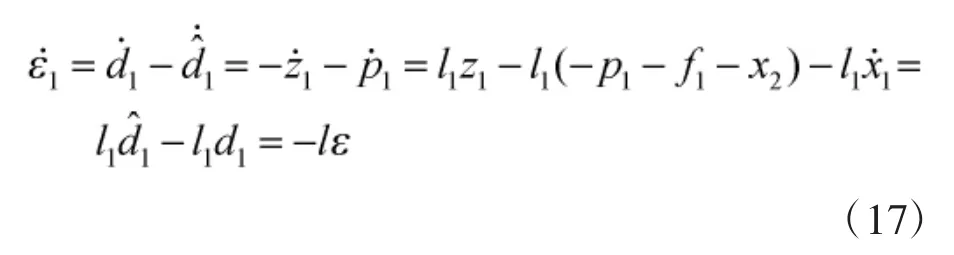
选取Lyapunov函数：

对等式两边进行求导：

可见，当l1＞0时估计误差全局稳定。

同理，使用同样的方法对式（12）的2式和3式的干扰进行估计可以得到。使用观测器对系统进行补偿的过程，如图2所示。

图2 基于干扰观测器补偿的控制系统结构图

3 反演滑模一体化控制器设计

Step 1.为了实现导弹制导目的，即导弹命中目标，需要零化视线角速率，即x1→0。本文采用滑模控制，现定义滑模面

考虑式（12）的1式对上式两边求导可得：

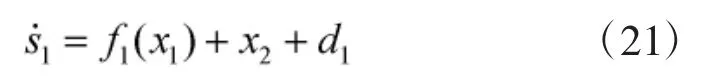
由于导弹的气动参数具有时变性，为了削弱抖振，并加快滑模面的收敛速度，选取具有自适应能力的趋近律法，其形式如下：

式中，r1＞0，采用反演设计方法，设计虚拟控制量，带入式（22）、式（23）可得：

Step 2.考虑闭环式（12）2式中的 x2与式（23）中的x2c存在偏差，为了消除x2c对x2的估计偏差，采用滑模控制方法，并定义如下滑模面：

将式带入式（24）得Step1精确滑模运动方程：

考虑式（12）的2式，对上式两边求导可得：

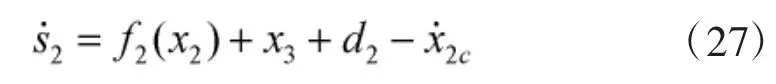
同理，对式（12）的第2个子系统，采用自适应指数趋近律，定义：

式中，k2＞0，σ2＞0 其中 σ2用2来估计，其形式如下：

式中，r2＞0，采用反演设计方法，设计虚拟控制量，由式（27）、式（28）可得：

将上式两边求导，并将式（31）带入得：

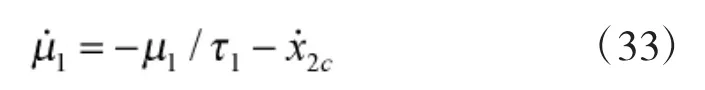
Step 3.考虑闭环式（12）3式中的 x3与式（30）中的x3c存在偏差，为了消除x3c对x3的估计偏差，采用滑模控制方法，并定义如下滑模面：

将式（34）带入式（24）得Step2中精确滑模方程：

考虑式（12）中的3式，对式（35）两边求导得：

同理，对式（12）的第3个子系统，采用自适应指数趋近律，定义：

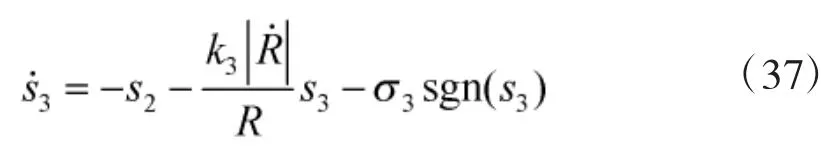
式中，r3＞0，采用反演设计方法，设计控制量 δz，由式（36）、式（37）可得：

将式（41）两边求导，并将式（40）带入得。

综上，得到基于反演滑模和非线性干扰观测器的制导控制一体化控制器。式（39）为最终的控制方程。

4 稳定性分析

证明：构造如下Lyapunov函数

对式（45）左右求导可得：

对式（46）左右求导可得：

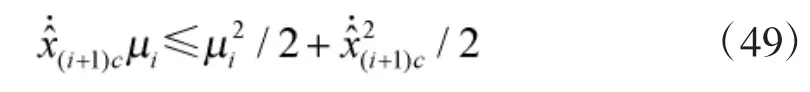
把式（49）带入式（48）可得：

5 仿真分析

为了验证本文所提出一体化控制算法的有效性，本节采用如下方式进行数值仿真验证。

假设导弹与目标均在纵向平面内运动。在末制导段，导弹的初始位置为（0，3 000）/m，导弹速度保持不变v=200 m/s。假设目标的初始位置为（3 000，0）/m，运动状态有3种：静止不动，以vt=80 m/s的匀速运动，以初速度vt=80 m/s加速度at=5 m/s2的匀加速运动。导弹的各项气动参数如下：

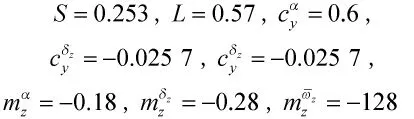
非线性干扰观测器、低通滤波器滤波时间常数及控制器参数为：

假设系统存在如下不同干扰，d1=0.1sin（2t），d2=0.1，d3为周期2 s幅值为0.1的三角波。为了验证所设计算法的有效性，对不同干扰的抗干扰能力和不同目标的追击能力，在系统存在干扰的情况下，分别针对有NDO和无NDO进行仿真。在3种运动状态下，两种控制器的对比仿真结果如表1所示。匀速运动情况下有干扰观测器的仿真曲线如图3～图10所示。

表1 3种状态两种控制器下的仿真结果

图3 正弦波干扰的实际值与估计值

图4 常值干扰的实际值与估计值

图5 三角波干扰的实际值与估计值

图6 弹-目相对运动轨迹

从表1中可以看出，在以上的几种情况下都可以保证脱靶量在1 m以内，表明控制器本身具有较强的鲁棒性。在目标状态一致，控制器存在NDO时，导弹的制导精度有明显提升；针对大机动目标，NDO可以明显减少遇靶时间；表明NDO对于提升控制器的性能有较大的作用。

图3～图5分别为干扰项 d1，d2，d3的实际值与估计值，从图中可以看出，针对不同类型的干扰，DNO都可以进行准确的估计。

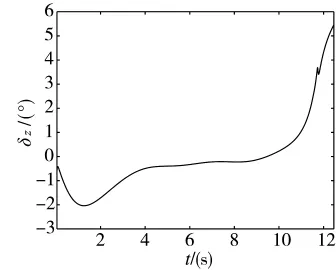
图7 导弹舵偏角变化曲线

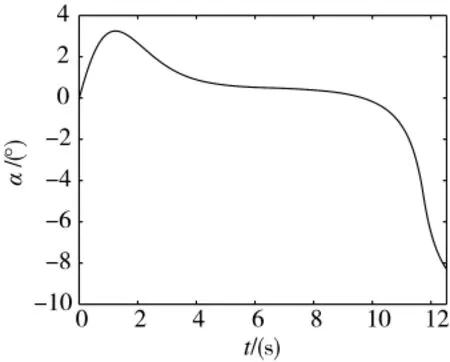
图8 视线角变化曲线

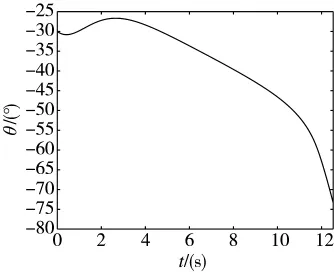
图9 导弹攻角变化曲线

图10 导弹弹道倾角变化曲线

从图6中可以看出，导弹飞行弹道比较平滑，近似直线飞行命中目标，追击时间较短。图7表明本文采用的方法，舵偏角较小且变化平缓，满足实际设计过程中舵偏角为±20°以内的约束条件。图8～图10表明视线角，攻角和弹道倾角变化比较平缓，符合系统设计要求。

基于以上分析，在目标不同运动状态下，存在干扰和不确定性影响的情况下，采用基于非线性干扰观测器和反演滑模的一体化设计方法，导弹可以快速精确地命中目标，而且具有较强的鲁棒性。

6 结论

本文研究了导弹在俯仰平面，针对系统存在的干扰及不确定性问题，设计基于非线性干扰观测器和反演滑模的一体化控制器。设计非线性干扰观测器对干扰进行补偿，并反馈至控制器，在反演滑模控制器设计的过程中，使用自适应趋近律方法减弱抖振，针对反演设计中产生的微分爆炸问题，采用动态面法，引入一阶低通滤波器代替对虚拟控制量进行求导。仿真结果表明，所设计的NDO可以对干扰进行精确地估计，所设计的控制器动态性能较好，鲁棒性强，制导精度高。