基于正交试验的空心线圈偏心误差影响因素敏感性分析

杨世海，胡 琛，焦 洋，李红斌，赵双双，陈 刚

(1. 国网江苏省电力有限公司电力科学研究院，江苏 南京 211103；2. 国家电网公司电能计量重点实验室，江苏 南京 211103；3. 华中科技大学 电气与电子工程学院，湖北 武汉 430074)

0 引言

空心线圈具有无磁饱和、线性度好、测量范围大、频带宽等优良特性，在电力系统及其他工业控制领域得到了诸多应用[1-4]。理论上，空心线圈的测量准确度不受载流体位置的影响，可以实现0.2级甚至更高的准确度等级。然而，一方面，由于一次载流体振动或者设计工艺等问题，实际中载流体可能出现偏心的现象；另一方面，理想空心线圈不可制造，由于不含集磁环铁芯，故空心线圈易受到载流体偏心的影响[5]。非理想空心线圈的偏心误差将对变电站保护、测量和计量单元的功能实现造成不利影响[6-8]。研究空心线圈偏心误差的影响因素，可以为提高空心线圈测量精度的措施提供理论依据。

目前，相关研究成果主要集中于空心线圈误差和偏心距离的关系。文献[9]分析了一次导体偏离空心线圈中心时，空心线圈精度的变化，并对实际空心线圈进行了偏心试验，得到了电磁屏蔽能够减小偏心误差影响的结论，但是该研究没有考虑空心线圈绕组不均匀度的影响；文献[10]推导了插板式空心线圈参数的计算方法，给出了偏心误差的计算公式，然而该研究同样没有计及绕组不均匀度的影响。近年来，一些学者研究了一次导体位置变动对非理想空心线圈性能的影响，得到了理论情况下一次导体位置变动引起的误差[11-12]，但是这些研究没有对空心线圈偏心误差影响因素的敏感性进行深入解析，对各个影响因素的作用程度还不够明确。另一方面，由于空心线圈偏心误差的影响因素较多，且各个影响因素之间交互作用，要区分各个影响因素的作用程度也非常复杂[13-14]。

正交试验法是实现多影响因素作用重要性分析的手段之一，被广泛应用于电气、煤炭、生物等领域[15-17]，可用于空心线圈偏心误差影响因素敏感性的分析。本文首先提出了空心线圈的传感模型，给出理想情况下空心线圈的互感系数；然后研究空心线圈偏心误差，并分析各个误差的影响因素；最后设计了正交试验方法，通过统计分析对偏心误差的影响因素进行敏感性分析。

1 空心线圈传感模型

空心线圈的传感方式基于全电流定律和法拉第电磁感应定律，通过感知由一次电流产生的穿过线圈的磁场，在线圈两端感应电压信号，根据电压信号重构一次电流信息。

空心线圈的基本等效电路如图1所示。图中，i为一次电流；is为二次电流；uo为空心线圈二次输出；LP为载流导体自感；Ls为线圈自感；M为载流导体和线圈之间的互感；Rs为线圈电阻；Rb为负载电阻；C为线圈分布电容。

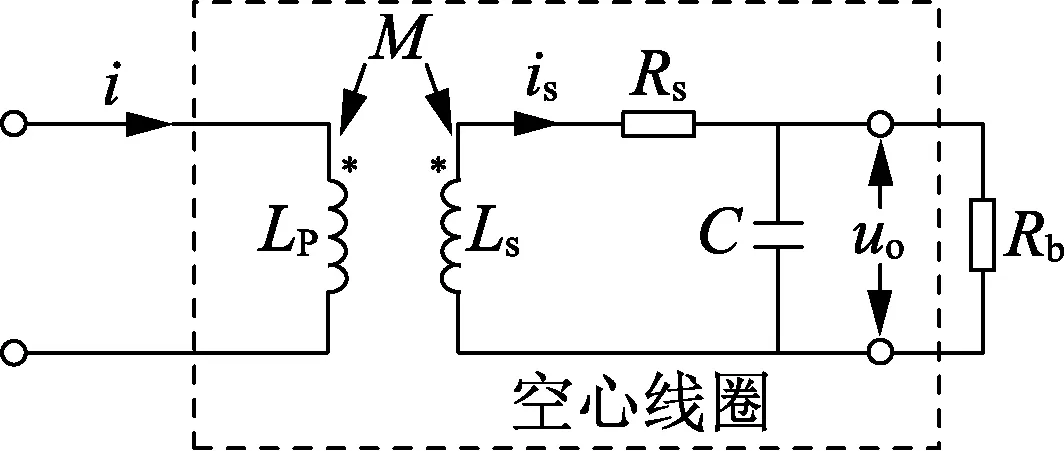
图1 空心线圈基本等效电路Fig.1 Basic equivalent circuit of air-core coil

在工频测量场合，一般不计及分布电容的影响，当Rb≫Ls时，空心线圈的输出可以近似为：

(1)

由式(1)可见，空心线圈输出和互感系数M以及一次电流对时间的微分成正比，只要对Uo(s)做积分运算即可还原一次电流i。另一方面，i、Rs、Rb不会受载流体偏心的影响，故空心线圈偏心误差实质上可等效为载流体偏心对互感的影响。

矩形截面的空心线圈性能稳定、易于制作、使用广泛，其几何结构示意图如图2所示。图中，r1为线圈绕组内壁和圆心之间的距离；r2为线圈绕组外壁和圆心之间的距离；h为线圈的高度。空心线圈的互感受线圈尺寸、结构以及一次载流体位置的影响。当空心线圈满足理想空心线圈的条件(截面均匀、绕组分布均匀)时，有以下关系式成立：

(2)

其中，μ0为真空磁导率；x为距离载流体中心的距离；φ1为穿过线圈的磁链；N为线圈匝数；S为线圈截面积。根据式(2)可以求得理想情况下空心线圈互感M1为：

(3)

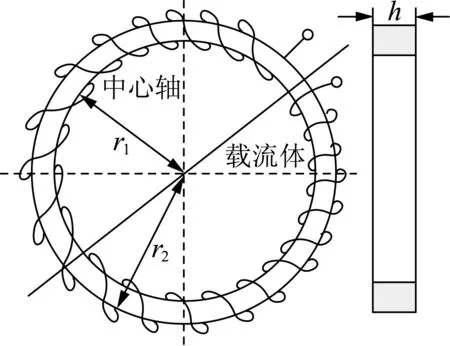
图2 空心线圈几何结构Fig.2 Geometrical structure of air-core coil

2 空心线圈偏心误差影响因素

实际应用中，空心线圈要实现绕组均匀分布是非常困难的，首先由于线圈制作工艺的局限性，空心线圈各绕组很难做到均匀分布；其次即使线圈通过数字印刷板设计技术实现了精确制造[18]，但是在线圈的第一匝和最后一匝之间由于要接入线圈负载，绕组必然存在不连续性。为了深入解析空心线圈偏心误差的影响因素，本节区分线圈绕组均匀和绕组不均匀2种情况，研究空心线圈的偏心误差及其影响因素。

2.1 绕组均匀情况下线圈误差

首先研究载流体偏心且绕组均匀情况下空心线圈互感的变化，磁场计算示意图如图3所示。图中，d为偏心距离；r、x1、θ、δ的定义见图3；B为电流产生的平均磁感应强度；B1为在线圈切向方向的磁感应强度。

图3 绕组均匀情况下空心线圈示意图Fig.3 Schematic diagram of air-core coil with even windings

根据安培环路定理以及图3中的几何关系，可以得到：

(4)

其中，φ2为此时穿过线圈的磁链；M2为线圈的互感器系数，由式(4)求得空心线圈互感如式(5)所示。

(5)

化简式(5)可以得到：

(6)

再求解式(6)所示积分，得到载流体偏心绕组均匀情况下空心线圈的互感为：

(7)

比较式(3)和式(7)可见：只要空心线圈的绕组均匀分布，即使载流体出现偏心情况，空心线圈的互感也不发生变化，即没有测量误差。

2.2 绕组不均匀情况下线圈误差

本节考虑载流体偏心且绕组不均匀情况下空心线圈互感的误差。为了简化分析，假设空心线圈不均匀绕组部分集中在图4所示的一个弧度为α的阴影区域，下文用α表示线圈的不均匀度。当载流体所在平面和不均匀绕组所在平面的相对位置为τ时，磁场求解依然可按照2.1节的思路，但此时沿线圈的积分路径不再是2π，而为τ+α/2～2π+τ-α/2。根据安培环路定理以及图4所示的几何关系可以得到：

(8)

其中，φ3为此时穿过线圈的磁链；M3为线圈的互感器系数，化简式(8)可以得到载流体偏心且绕组不均匀情况下空心线圈的互感M3，如式(9)所示。

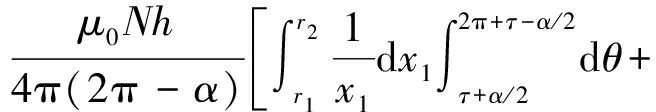
(9)

图4 绕组不均匀情况下空心线圈示意图Fig.4 Schematic diagram of air-core coil with uneven winding

实际中考虑制造工艺或制造水平的问题，空心线圈可能存在多个不均匀区域。图5中的阴影区域表示空心线圈的2个不均匀区域，且不均匀度均为α，载流体平面和2个不均匀绕组所在平面的相对位置分别为τ1、τ2时，积分路径分别改变为τ1+α/2～τ2以及τ2+α～2π+τ1-α/2，从而可得到以下关系：

图5 存在2个绕组不均匀情况下空心线圈示意图Fig.5 Schematic diagram of air-core coil with two uneven windings

(10)

其中，φ4为此时穿过线圈的磁链；M4为线圈的互感器系数，化简式(10)可得到此时线圈互感M4如式(11)所示。

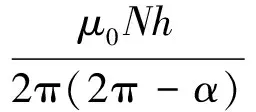
(11)

由式(9)和式(11)可见：当绕组分布不均匀且载流体出现偏心现象时，空心线圈互感不再等于式(3)的计算结果，两者之间的误差e定义如式(12)所示。

(12)

2.3 影响因素分析

当线圈结构参数固定而绕组分布不均匀时，空心线圈偏心误差的影响因素包括3个因素：载流体偏心距离d；空心线圈绕组不均匀度α(以下简称为不均匀度)；载流体和不均匀绕组的相对位置τ1以及τ2(以下简称为相对位置，为了简化分析，固定τ2=90°)。

假设空心线圈的尺寸参数如下：内半径r1=40 mm，外半径r2=60 mm，厚度h=20 mm；线圈匝数N=500匝。固定不均匀度α=0.5°，载流体偏心距离d在0～0.8r1范围内变化、相对位置τ1在0°～180° 范围内变化时，空心线圈偏心误差e和偏心距离、相对位置的关系如图6所示。

图6 偏心误差和偏心距离、相对位置的关系Fig.6 Relationship among eccentricity error,eccentric distance and relative position

当固定载流体偏心距离d=0.25r1、不均匀度α在0.1°～1° 范围变化、相对位置τ1在0°～180° 范围内变化时，空心线圈偏心误差e和不均匀度、相对位置的关系如图7所示。

图7 偏心误差和不均匀度、相对位置的关系Fig.7 Relationship among eccentricity error,inhomogeneity and relative position

当固定相对位置τ1=0°、载流体偏心距离d在0～0.8r1范围内变化、不均匀度α在0.1°～1° 范围内变化时，偏心距离、不均匀度对空心线圈偏心误差e的影响如图8所示。

图8 偏心误差和偏心距离、不均匀度的关系Fig.8 Relationship among eccentricity error,eccentric distance and inhomogeneity

根据以上理论分析及仿真结果可知：当线圈不均匀度α固定时，偏心距离d越大，则偏心误差越大，如果不偏心，相对位置不会对偏心误差造成影响；当偏心距离d固定时，偏心误差在相对位置168°附近出现最大值，最大相对误差约为0.18%；当相对位置τ1固定时，偏心距离越大，则偏心误差越大，如果不偏心，不均匀度不会对偏心误差造成影响。

3 影响因素敏感性分析

本节分析偏心距离、不均匀度和相对位置这3个主要影响因素对空心线圈偏心误差的影响程度。由于影响因素较多，且各影响因素存在相互作用，如果逐个方案试验，则试验次数较多，数据处理复杂。为此，本文基于正交试验法，以偏心误差为指标，通过正交试验表确定试验方案，对3个影响因素的敏感程度进行分析。

3.1 正交试验方案

设计了一个矩形截面空心线圈，样品骨架尺寸为40 mm×60 mm×20 mm(内径×外径×厚度)，线圈由0.5 mm漆包铜线绕成，匝数N=500匝，线圈的变比为100 A/4 V。测试系统原理图如图9所示，在额定电流100 A情况下，将空心线圈输出和标准电磁式互感器(TA)输出接至电子式互感器校验仪[19]，标准电流转换器包括一个5 A/0.05 A的小互感器以及一个10 Ω高精度的无感电阻，0.02级标准TA变比为100 A/5 A。空心线圈输出经过积分环节[20]后，和标准TA的数据同时被NI PCI-4474采集卡采集，采集卡将采集后的数字信号通过RTSI接口发送给上位机，上位机基于LabVIEW环境[21]实现数据基波分量的提取、空心线圈误差计算、结果显示等功能。

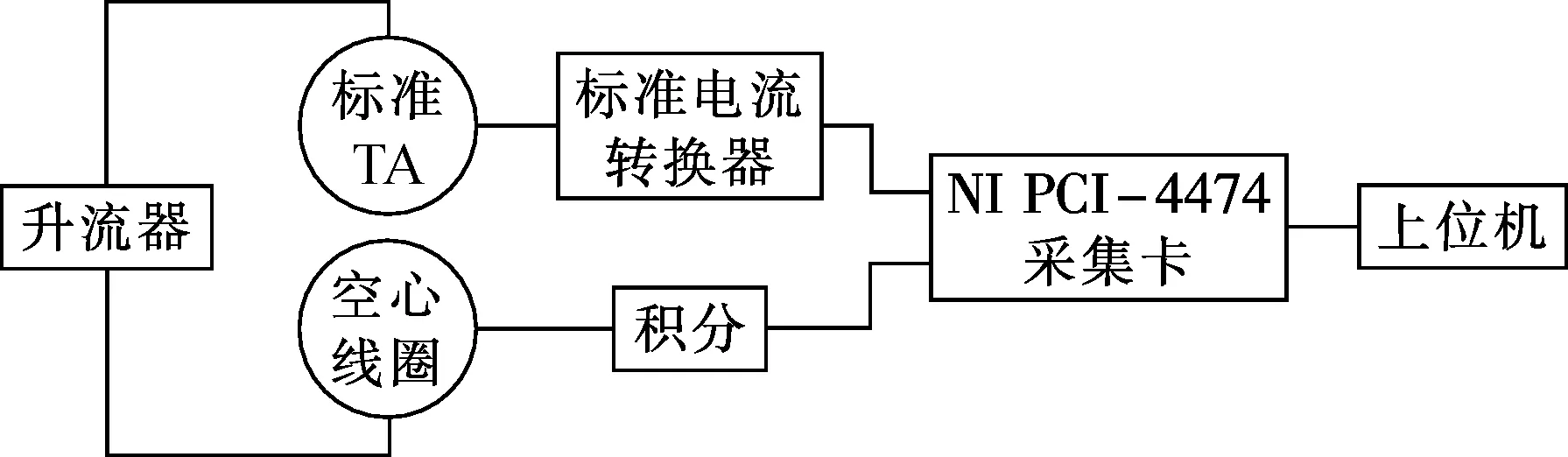
图9 测试系统原理图Fig.9 Schematic diagram of testing system

由前文理论分析可知，空心线圈偏心误差有3个影响因素，本试验中每个影响因素选取了5个水平值，本试验为3因素5水平试验。正交试验方案首先需要明确影响因素的水平值。试验过程中，偏心距离和相对位置通过调整载流体位置进行改变，不均匀度通过改变绕组匝数的方式进行调节。对于偏心距离而言，由仿真结果可知，偏心距离越大，则误差越大，为了得到显著的试验结果，应当尽量增大偏心距离，又考虑到空心线圈内径(40 mm)的约束，偏心距离调整范围在4～32 mm之间，本试验选择4 mm、10 mm、16 mm、22 mm、32 mm这5个水平；对于相对位置而言，由于对称性，只需要考虑0°～180°水平，而180°～360°的结果和0°～180°一致，本试验选取0°、45°、90°、135°、180°这5个水平；对于不均匀度而言，虽然实际运行过程中不均匀度非常小(如前文数值仿真选取的1°)，但是一方面为了得到更大的空心线圈输出，有利于减少采集卡的量化误差以及上位机计算误差，另一方面1° 的不均匀度难以控制，故试验中增大了不均匀度水平，本试验选取了0°～60° 区间内的0°、15°、30°、45°、60° 这5个水平。表1列出了各影响因素的水平值。

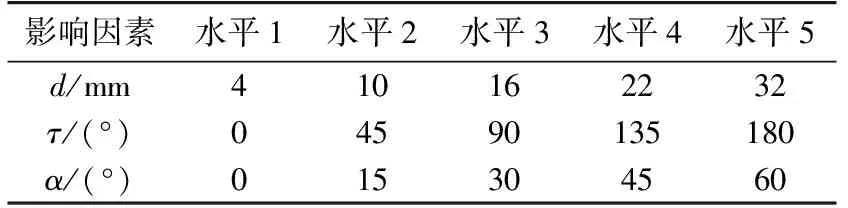
表1 影响因素水平值Table 1 Level values of influencing factors

采用L25(5∧6)正交试验表进行正交试验方案设计，试验方案如表2所示，其中空列表示没有影响因素作用，反映随机因素引起的误差。以此为依据建立各影响因素的试验方案，试验计算结果如表3所示。表中，Kjl为第j(j=2，3，4，5)列中影响因素相应于l水平的5个试验结果之和，记：

(13)

其中，K为全体试验结果之和，与列数无关。又令：

(14)

其中，Yi为各次试验结果。由式(14)可以得到：

(15)

3.2 方差分析

根据正交试验理论，对表2中25次试验的结果进行方差分析，各中间变量计算结果见表4。表中，平方和为式(14)中的Sj，偏差的平方和与空列Sj之和对应；自由度由影响因素所取的水平数减1得到；均方和为平方和除以自由度后的值；F值由各影响因素的均方和除以偏差均方和得到。

表2 正交试验方案表Table 2 Schemes of orthogonal test

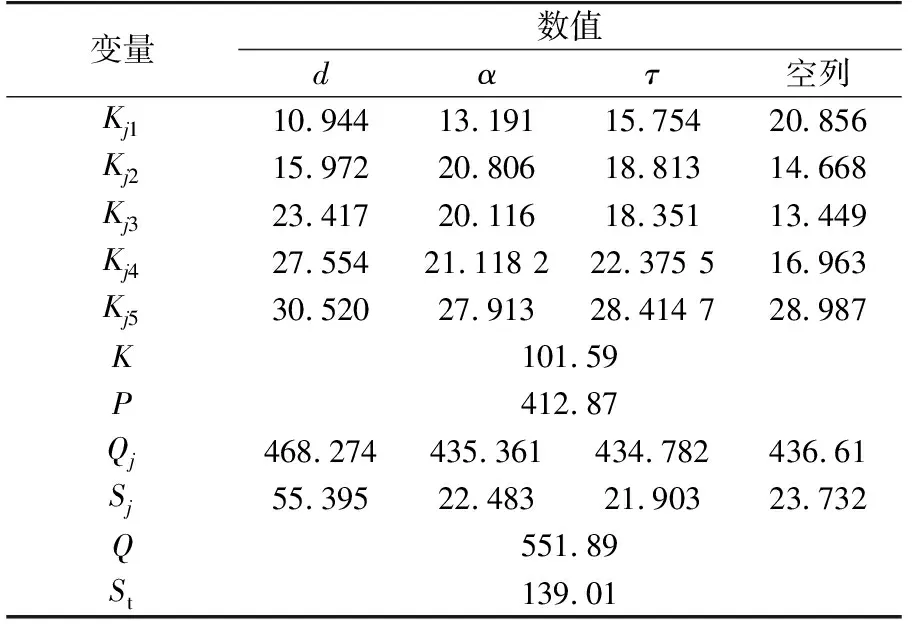
表3 正交试验结果Table 3 Results of orthogonal test

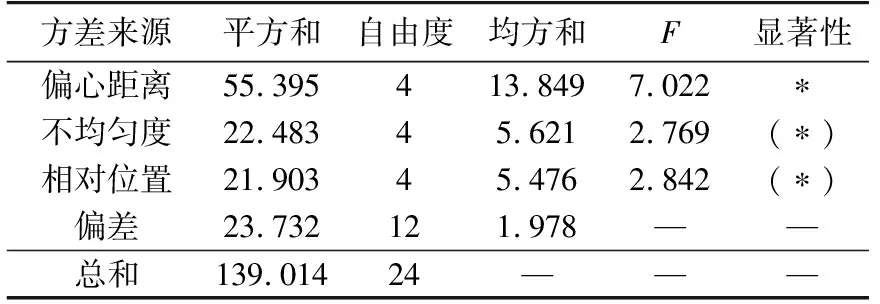
表4 方差分析结果Table 4 Results of variance analysis

假设各影响因素对空心线圈偏心误差影响不显著，查表可得F的临界值为：

(16)

其中，F0.90(4,12)和F0.95(4,12)分别为显著性水平0.1和显著性水平0.05时的临界值；“显著性”一列符号“(*)”、“*”分别表示在显著性水平0.1、0.05下检验的结果是拒绝原假设的，即该因素所处水平对空心线圈误差情况的影响显著。根据F分布检验结果得到如下结论：

a. 偏心距离对空心线圈误差情况的影响最显著，不均匀度和相对位置对空心线圈误差情况的影响比较显著；

b. 对比不均匀度和相对位置因素的F值可得，3个因素中不均匀度对空心线圈误差情况的影响程度最小；

c. 为了控制空心线圈偏心误差，应优先保证导体中心与线圈中心的一致性。

4 结论

a. 绕组均匀的情况下，即使载流体出现偏心情况，空心线圈也不会产生误差；

b. 绕组不均匀的情况下，偏心距离、不均匀度、相对位置将影响空心线圈偏心误差；

c. 3个影响因素对偏心误差均有显著影响(0.1显著性水平)，其中偏心距离对空心线圈误差的影响程度最大，其次为相对位置，不均匀度的影响程度最低，实际运行过程中应考虑固定载流体位置以减小偏心误差；

d. 结构参数对空心线圈偏心误差也有较大的影响，但是由于试验中线圈结构参数(内径、外径、厚度)难以调整，故本文没有计及结构参数的影响。今后的研究中将考虑利用PCB制作技术生产多种不同规格的空心线圈，分析结构参数的影响程度。