闭环控制下单相VSC低次谐波分析模型与抑制策略

钟 庆,冯俊杰，王 钢，李海锋

(华南理工大学 电力学院,广东 广州 510640)

0 引言

单相电压源型换流器SPVSC(Single-Phase Voltage Source Converter)能实现交直流能量的可逆变换,具有运行控制灵活的优点，在新能源并网[1-3]和电力牵引[4]中得到了越来越广泛的应用。然而，由于电力电子器件的强非线性，SPVSC在实现能量转换的同时也带来了谐波含量过大的问题，对电网运行造成了负面影响[5]。因此，建立SPVSC的谐波分析模型研究其谐波特性，并制定有效的谐波抑制策略，可为SPVSC的推广应用提供有力的理论支撑。

三相电压源型换流器(VSC)在电网电压平衡的正常运行情况下将产生高次特征谐波，一般可以通过高通滤波器滤除[6]。与三相VSC不同，SPVSC正常运行时，会在产生高次谐波的同时，产生低次谐波，对电网造成污染[7-8]。针对SPVSC谐波产生的原因，文献[9-11]通过双重傅里叶分解和贝塞尔函数推导开环控制下SPVSC交流侧电压谐波的计算公式，能够得到谐波电压的理论计算结果，但计算过程中未计及闭环控制过程。文献[12-13]考虑了SPVSC的电压电流双闭环控制，得到控制器输出的脉宽调制PWM(Pulse Width Modulation)信号，并分析了PWM信号的谐波分量，从功率平衡的角度分析了各次谐波产生的原因，但并未考虑控制参数对谐波含量的影响。针对SPVSC产生的低次谐波，改进控制策略是抑制谐波电流的有效方法，其中最常用的是比例谐振控制[12-13]。文献[14]提出了电流环采用嵌入式重复控制和电压环采用N次陷波器相结合的控制算法，实现了交流侧谐波电流的抑制。文献[15-16]认为SPVSC直流侧电压2次谐波使得电压外环生成的指令电流存在3次谐波，因此提出引入直流侧2次谐波反馈环节以抑制交流侧谐波电流。上述谐波抑制策略均是通过改进控制环特性实现SPVSC交流侧谐波的抑制。另一个解决思路是在PWM信号中叠加谐波信号以抑制交流侧谐波电流，但这种方法需要反复试凑才能取得较好的效果。如果能通过谐波分析模型理论计算出需叠加的调制信号的数值，则可在不改变控制环的基础上实现谐波抑制，大幅提高控制效率。

为此，本文首先分析了闭环控制下的开关函数动态相量，将SPVSC的时域模型转化成动态相量模型，建立了SPVSC动态相量谐波分析模型；然后，基于谐波分析模型，分析了SPVSC交流侧各低次谐波电流分量与直流侧各低次谐波电压分量的相互作用关系，以及控制环参数对交流侧谐波电流分量的影响；然后，通过切断外界干扰源和内部传递通路的方式，在PWM信号中叠加低次谐波信号并定量计算出叠加分量的大小，实现交流侧谐波电流的抑制；最后通过仿真和实验结果验证本文所提出的分析模型的正确性和谐波抑制策略的有效性。

1 SPVSC谐波分析模型

1.1 SPVSC时域模型

本文研究的SPVSC拓扑结构如图1所示，为单相H桥式VSC。图1中，Us为系统电压；R、L分别为交流侧等效电阻和滤波电感；IR、URac分别为SPVSC交流侧电流、电压；Cdc、Rdc分别为SPVSC直流侧电容、负载等效电阻；Idc、Il分别为直流侧电流和负载电流；VT1、VT2、VT3、VT4为换流器的4个电力电子器件。

图1 SPVSC拓扑结构图Fig.1 Topology of SPVSC

SPVSC时域模型如式(1)所示。

(1)

采用开关函数描述交直流侧的相互作用，则式(1)中URac和Idc分别为：

(2)

其中，SR为SPVSC的开关函数，当VT1和VT4导通时SR=1，当VT2、VT3导通时SR=-1。开关函数SR与控制策略有关，由控制器输出的PWM信号确定。

本文采用如图2所示的电压外环电流内环的双闭环控制策略。直流电压外环控制采用比例积分(PI)调节器生成的电流幅值参考值Im_ref与锁相环(PLL)捕获的系统电压Us相位余弦值cosθ相乘得到电流内环的电流参考值It_ref；电流内环控制采用比例(P)调节器。

图2 电压电流双闭环控制结构Fig.2 Double closed-loop control structure of voltage and current

需要特别说明的是，考虑到实际工程中网侧电压采样的相位延迟问题，本文中电网电压前馈采样值Ust采用其基波有效值Urms与PLL捕获的正弦值cosθ相乘的方式获得。Ust减去电流内环比例调节器输出量后除以直流侧电压参考值Udc_ref得到VSC的调制信号Um。则控制器生成的调制信号Um为：

Um=[Ust-Kip(It_ref-IR)]/Udc_ref

(3)

1.2 SPVSC动态相量谐波分析模型

将由式(1)和(2)描述的SPVSC时域模型转化为动态相量模型，则交流侧电流和直流侧电压的k阶动态相量方程为：

(4)

其中，ωs为工频角速度；〈·〉k表示该变量的k阶动态相量。

〈UdcSR〉k和〈IRSR〉k分别为直流侧电压、交流侧电流与开关函数的卷积，体现SPVSC交直流侧的相互作用，其计算公式分别如式(5)、式(6)所示。

(5)

(6)

本文采用固定开关频率下的正弦波PWM，则开关函数的动态相量由Um确定[17]，其表达式为：

(7)

由于Ust和It_ref只有基波分量，因此〈Ust〉1≠0，〈It_ref〉1≠0，其余分量均为0。由于本文只分析SPVSC在13次以内的低次谐波分量，因此忽略开关函数动态分量中的高次分量，式(7)可简化为：

(8)

将式(8)代入式(4)，可得交流侧电流和直流侧电压的k阶动态相量方程为：

(9)

(10)

(11)

(12)

求解式(9)和(10)可得到交流侧电流和直流侧电压的各阶动态相量〈IR〉k、〈Udc〉k，即为交流侧电流和直流侧电压各次谐波分量的解析计算结果，因此该SPVSC动态相量模型可作为其谐波分析模型。

2 SPVSC谐波产生机理分析

2.1 SPVSC谐波传递机理

由式(9)可得直流侧直流电压分量的计算公式如式(13)所示。

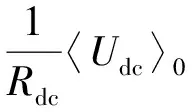
(13)

其中，等号左侧变量为直流侧电压的直流分量〈Udc〉0，等号右侧中变量只有交流侧的基波电流分量〈IR〉1，由此可见直流侧电压的直流分量与交流侧的基波电流分量存在相互作用。

由式(10)可得交流侧的基波电流分量计算公式如式(14)所示。

(14)

其中，等号左侧变量为交流侧的基波电流分量〈IR〉1，等号右侧含有2个变量，分别为直流侧电压的直流分量〈Udc〉0和2次谐波分量〈Udc〉2。因此，交流侧基波电流除了与直流侧直流电压分量存在相互作用外，还作用于直流侧2次谐波电压。

直流侧2次谐波电压和交流侧3次谐波电流的计算公式分别如式(15)和式(16)所示。

(15)

(R+j3ωsL+Kip)〈IR〉3=

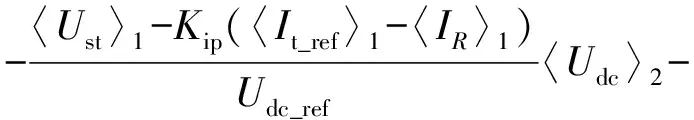
(16)

式(15)等号右侧状态变量除了〈IR〉1外还有〈IR〉3，可见直流侧2次谐波电压除了与交流侧基波电流存在相互作用外，还与交流侧3次谐波电流存在相互作用关系。同理，由式(16)可见交流侧3次谐波电流除了与直流侧2次谐波电压相互作用外，还与直流侧4次谐波电压存在相互作用关系。电网侧3次背景电压谐波也会作用于交流侧3次谐波电流。因此，SPVSC交流侧谐波电流与直流侧谐波电压的产生原因及相互作用规律如图3所示。图中，Udci为直流侧i次谐波电压分量，IRi为交流侧i次谐波电流分量，二者均为SPVSC的状态变量；Usi为交流侧电源i次谐波电压分量；单箭头表示外部激励对谐波产生的影响，双箭头表示2个状态变量之间的相互作用。SPVSC的低次谐波产生可以分为外部激励和内部相互作用2种关系。由内部相互作用关系可知，正常运行时SPVSC将在交流侧产生一系列奇次谐波电流，在直流侧产生一系列偶次谐波电压。由外部激励关系可知，当系统存在背景谐波时，SPVSC产生的谐波量将增加，加剧对系统的谐波污染。

图3 SPVSC谐波产生与相互作用规律Fig.3 Generation and interaction law of harmonic of SPVSC

2.2 控制参数对交流侧电流谐波的影响

由式(16)可知，电流内环的控制参数Kip的大小将会对交流侧3次电流谐波产生直接影响。由于稳态的情况下，交流侧基波电流无限接近于指令电流值，在分析Kip对交流侧谐波电流的影响时，等号右侧的Kip(〈It_ref〉1-〈IR〉1)/Udc_ref可忽略不计，推广到N次(N=3,5,…,13)谐波分量，交流侧电流谐波表达式可作如下简化：

(17)

由此可知，电流内环比例调节增益Kip越大交流侧电流谐波幅值越小，Kip越小交流侧电流谐波幅值越大。并且，由式(14)可知，电流内环比例调节增益的大小对交流侧基波电流的大小无影响。

3 谐波抑制策略

为减小SPVSC对电网的谐波污染，需要抑制交流侧谐波电流的产生。由SPVSC谐波产生机理可知，交流侧谐波电流主要由交直流侧相互作用和外部激励2种途径产生。因此，本文提出了在PWM信号中叠加低次谐波分量，同时切断外部激励和内部传递通路，以抑制交流侧低次谐波电流。

在稳态的情况下，交流侧电流动态相量微分项为0，以交流侧N次(N=3，5，…，13)谐波电流为例，由式(4)可得到其计算公式为：

(18)

由此可知，如果能使式(18)等号右侧为0，即可切断交直流侧谐波的相互作用以及背景谐波电压对SPVSC的影响通路，可有效抑制交流侧N次谐波电流。则由式(7)和(9)可得PWM信号应叠加的N次谐波信号〈ΔS〉N，如式(19)所示。

〈Udc〉0

(19)

综合以上分析，本文提出了在PWM信号中叠加低次谐波分量的前馈补偿控制策略，以抑制交流侧电流的低次谐波，其控制框图如图4所示。通过实时检测直流侧电压谐波分量和交流侧电压背景谐波分量，根据式(19)得到在PWM信号中需要叠加的N次谐波分量的幅值和相角，从而实现SPVSC交流侧谐波电流的动态抑制。

图4 注入N次谐波控制框图Fig.4 Control block diagram of injecting N-order harmonic wave

4 仿真和实验验证

4.1 谐波分析模型仿真验证

为验证模型的正确性，利用MATLAB/Simulink建立SPVSC仿真模型，其中网侧采用有效值为220 V的工频交流电压，交流侧电阻和电感分别为0.02 Ω、3 mH，直流侧电容为3 400 μF，负载为10 Ω的电阻。设定载波频率为1 050 Hz，采用如图2所示的电压电流双闭环控制策略，得到交流侧谐波电流和直流侧谐波电压的仿真结果和理论计算结果分别如表1和表2所示。由表1、2可见：交流侧谐波电流与直流侧谐波电压的幅值和角度仿真结果与理论计算结果基本吻合；交流侧存在一系列低次的奇次谐波电流，其中3次谐波电流含量占了主导地位，随着谐波次数增加谐波含量减小；直流侧存在一系列低次的偶次谐波电压，其中2次谐波电压含量最为明显，同样随着谐波次数的增加谐波含量明显减小。因此，电压电流双闭环控制下SPVSC低次谐波分析模型的正确性得到了验证。

表1 交流侧谐波电流仿真和理论计算结果对比Table 1 Comparison of AC harmonic currents between theoretical and simulative results

表2 直流侧谐波电压仿真和理论计算结果对比Table 2 Comparison of DC harmonic voltages between theoretical and simulative results

4.2 谐波产生与传递机理验证

为了验证SPVSC谐波传递规律的正确性，分别在网侧注入幅值为0.05 p.u. 的3次和5次电压背景谐波，得到交流侧电流和直流侧电压的谐波频谱图如图5所示。由图可知：当电网含3次背景谐波时，交流侧3次电流谐波显著增大，并且在交直流侧的相互作用下，直流侧电压4次谐波幅值显著增大，同时传递回交流侧5次电流谐波，但经过二次传递后作用关系大幅削弱；同理，当电网含5次背景谐波时，在交流侧5次电流谐波的作用下直流侧产生了明显的6次电压谐波，但当传递到交流侧7次电流谐波时，作用关系削弱。上述结果验证了图3所示的谐波传递规律的正确性。

图5 含3、5次背景谐波的网侧电压Fig.5 Grid side voltage containing 3rd- or 5th-order harmonic

为了验证电流内环比例调节增益大小对交流侧谐波电流的影响，分别取Kip为3、5、7、9、11、13，得到交流侧电流基波和谐波分量幅值变化趋势如图6所示，其中为了更好地观察谐波变化情况，仿真中在网侧加入了5次电压背景谐波。由图可知，随着Kip的增大，交流侧电流谐波不断减小，但对交流侧电流基波无明显影响，由此验证了本文机理分析的正确性。

图6 交流侧电流随Kip的变化趋势Fig.6 AC side currents changing along with Kip

4.3 谐波抑制策略仿真验证

针对4.1节中的SPVSC仿真模型，在PWM信号中叠加谐波分量，对比抑制策略实施前后交流侧电流谐波含量，对其有效性进行验证，并通过改变系统工况验证其动态补偿效果。初始时，系统未加入谐波抑制环节，网侧电压含有幅值为0.1 p.u. 的3次背景谐波和幅值为0.05 p.u. 的5次背景谐波；0.4 s时，加入谐波抑制环节，在PWM信号中叠加谐波分量；0.5 s时，网侧电压的背景谐波发生突变，仅含幅值为0.05 p.u. 的5次背景谐波；0.7 s时，网侧电压背景谐波突变为0，直流侧负载电阻由10 Ω突变为6.67 Ω； 0.9 s时，再次关断谐波抑制环节。仿真验证结果如表3和图7所示(图7中，纵轴为标幺值)。

表3 PWM信号中叠加N次谐波分量前后的交流侧电流值Table 3 AC side currents before and after injecting N-order harmonic wave in PWM signal

图7 PWM信号中所叠加谐波分量的动态变化波形Fig.7 Harmonic injection components of PWM signal

观察表3可知，在加入谐波抑制环节之前，交流侧含有大量的3、5次谐波，幅值分别为6.48 A和2.85 A。在PWM信号中叠加3、5次谐波分量后，谐波得到有效抑制，3、5次电流谐波幅值分别下降为0.37 A和0.09 A。在0.5 s和0.7 s时电网侧背景谐波和负载电阻发生突变，但是谐波抑制效果并未受到影响。由图7可知，PWM调制波叠加分量〈ΔS〉N能快速跟踪系统工况的变化，有效抑制谐波。上述仿真结果验证了本文所提谐波抑制策略的有效性。

4.4 谐波抑制策略实验验证

本文采用的实验平台详见附录。交流侧电感值为6 mH，直流侧电容和负载电阻分别为3 400 μF和75 Ω，调制波频率为50 Hz,载波频率为7.5 kHz。换流器采用日本三菱公司的智能功率模块(IPM)，控制器型号为德州仪器(TI)的TMS320F28335，控制策略与仿真相同。

系统电压直接引入有效值为220 V的市电电压，通过检测可知最明显的背景谐波电压为5次谐波电压，其幅值为0.015 p.u.。因此在实验中主要针对该次谐波对所提抑制策略进行验证。通过实时监测交直流侧电压谐波分量，计算在PWM信号中叠加谐波分量的幅值和相角，并施加于换流器。使用FLUKE435测量SPVSC交流侧电压和电流并对其进行频谱特性分析，得到交流侧电压电流波形如图8所示，交流侧电流频谱特性如图9所示。

图8 PWM信号叠加谐波前、后交流侧电压电流波形图Fig.8 AC side voltage and current before and after injecting harmonic wave

图9 PWM调制叠加波前、后交流侧电流频谱Fig.9 Comparison of harmonic spectrum before and after modulated wave injection

实验结果显示，通过在PWM信号中叠加谐波后，交流侧电流的电流谐波总畸变率(THD)由7.3%下降到5.4%，交流侧5次谐波电流幅值由0.67 A下降到0.24 A，由此可见交流侧电流5次谐波电流得到了有效的抑制，验证了本文所提谐波抑制策略的有效性。但由于本文在理论分析中并未考虑控制器死区、叠加谐波时滞等影响，因此无法完全消除交流侧5次谐波电流。同时可以说明，本文在PWM信号中叠加5次谐波后，对其他次谐波电流无法起到抑制作用。

5 结论

本文通过建立闭环控制下的SPVSC动态相量谐波分析模型，揭示了SPVSC交流侧谐波电流和直流侧谐波电压的产生机理及相互作用关系。SPVSC的谐波产生可以分为外部激励和内部相互作用2个方面。在内部相互作用下，SPVSC在交流侧产生一系列奇次谐波电流，在直流侧产生一系列偶次谐波电压。在外部激励作用下，背景谐波将显著增加谐波电流含量。另外，控制环参数也会对谐波含量产生影响，电流内环比例调节增益Kip大小与交流侧电流谐波幅值大小呈反比例关系。

通过切断外部激励和内部传递通路，在PWM调制信号中定量增加低次谐波分量，可实现交流侧低次谐波电流的抑制。该策略具有易于求解与实现的优点，对SPVSC谐波抑制效果明显。

附录见本刊网络版(http:∥www.epae.cn)。