CdTe量子点与微囊藻毒素-LR抗体的偶联及其相互作用的研究

李 莹，孙嘉笛，孙秀兰*，，张银志

（1.江南大学 食品学院，江苏 无锡 214122；2.食品科学与技术国家重点实验室，江南大学，江苏 无锡 214122）

量子点（Quantum dots，QDs）是一类由 II-VI族（如 CdSe、CdTe、ZnSe、CdS 等）或 III-V 族（如 InAs、InP等）以及Si等元素组成的均一或核壳结构的纳米颗粒，是近年发展起来的一种新型纳米材料，它具有激发光谱宽，发射光谱窄，光稳定性好等众多优点[1-3]，自从有学者将量子点与生物分子成功偶联之后，量子点就逐渐开始被应用于荧光标记、免疫测定等生物学领域。然而量子点的荧光特性在生物环境下易猝灭[4]，从而限制了量子点的生物应用范围。所以作者在制备量子点-抗体荧光探针的同时，也对量子点与抗体之间的相互作用机理进行了研究。

作者首先合成了CdTe量子点，接着采用纯化后的量子点与微囊藻毒素-LR抗体进行偶联，分别研究了不同条件对偶联效果的影响，然后通过紫外-可见吸收光谱、荧光光谱对比了偶联前后的光谱变化，借助聚丙烯酰胺凝胶电泳（SDS-PAGE凝胶电泳）来鉴定偶联产物。与此同时，结合经验公式，深入分析了QDs与抗体的相互作用机理。通过这些研究，为今后量子点在生物学领域方面的推广应用提供了一些参考。

1 材料与方法

1.1 实验材料

1-（3-二甲氨基丙基）-3-乙基碳二亚胺盐酸盐（EDC）、巯基乙酸、十二烷基磺酸钠、丙烯酰胺、N-N亚甲基双丙烯酰胺、TEMED、过硫酸铵、考马斯亮蓝R-250、甲醇、甘氨酸、氯化钠等，均购自国药集团；微囊藻毒素-LR（MC-LR）抗体为实验室免疫所得；所用试剂均为分析纯，实验用水为超纯水。

1.2 仪器

GRP-9050型隔水式恒温培养箱，上海森信实验仪器有限公司产品；F-7000型荧光分光光度计，日立高新技术公司产品；UV-1800型紫外-可见分光光谱仪，日本岛津产品；DYCZ-24D垂直板电泳槽，北京六一仪器厂制造；Tanon GLS-2010凝胶成像仪，上海天能科技有限公司产品；5424冷冻离心机，德国Eppendorf公司产品；TecnaiG2F20s-TWIN透射电镜，美国FEI公司产品；PB-10C标准pH计，上海精密科学仪器有限公司产品。

1.3 实验方法

1.3.1 CdTe量子点的制备 将0.12 g硼氢化钠溶于5 mL超纯水中，在氮气的保护下加入30 mg碲粉，常温磁力搅拌反应直至黑色碲粉完全溶解，反应液为无色 （或粉红色）透明，即得到碲氢化钠（NaHTe）溶液，备用。 称取一定量的 CdCl·2.5H2O，用超纯水溶解于三口烧瓶中，加入适量巯基乙酸（TGA），用0.1 mol/L的NaOH调节溶液pH值至最佳，通氮气20 min左右，排出体系中的氧气，然后在磁力搅拌以及氮气的保护下迅速加入新鲜制备的碲氢化钠溶液，100℃加热回流一定时间。避光冷却至室温，即可得到澄清透明的CdTe量子点（CdTe QDs）溶液[5]。

1.3.2 CdTe量子点荧光探针的制备及纯化 以巯基乙酸（TGA）为修饰剂所制备的CdTe QDs，表面有羧基覆盖，在缩合剂EDC的作用下能与微囊藻毒素-LR抗体（MC-LR）的氨基反应，从而实现量子点与抗体的共价偶联。由于量子点的粒径要远远小于抗体，所以对偶联物进行超滤离心，截留下与抗体偶联成功的量子点。具体操作如下[6]：在2 mL CdTe量子点溶液中，加入30 μL EDC，37℃反应30 min，使量子点充分活化，然后加入30 μL MC-LR抗体，37℃反应一定时间，反应体系中，QDs∶MC-LR抗体∶EDC的摩尔比为1∶15∶200，最后加入终质量浓度为0.1 mg/dL的BSA进行封闭。将溶液放入10×104的超滤离心管中，10 000 r/min离心10 min，截留物复溶于PBS中（pH7.4），即得到纯化后的QDs-MC-LR抗体。

1.3.3 量子点及量子点-抗体偶联结果的分析 分别测定CdTe QDs的紫外可见吸收光谱和荧光光谱，并借助透射电镜表征其形貌。

分别测定CdTe QDs与 QDs-Ab的紫外可见吸收光谱和荧光光谱，对比偶联前后光谱变化。

以QDs为对照，采用SDS-聚丙烯酰胺凝胶电泳鉴定偶联物。

1.3.4 量子点与抗体的光谱分析 在不同温度下，固定微囊藻毒素抗体的浓度，向其中加入不同浓度的CdTe量子点，分别测定体系的吸收光谱和荧光光谱。对光谱进行分析，从而对量子点与抗体之间的相互作用有进一步了解。

2 结果与分析

2.1 CdTe量子点的表征

量子点的粒径对其荧光，吸收光谱和荧光光谱都有着很大的影响，制备过程中，改变制备条件，就可以得到不同粒径的量子点，粒径从小到大，荧光依次从绿到红，吸收光谱和荧光光谱也随之改变。本文中以回流3 h所制备的CdTe量子点为例，对其进行表征。

2.1.1 外观 观察CdTe量子点在日光下（左）和紫外灯下（右）时的图片，由图1可知，在日光下，量子点为橘红色澄清透明的溶液，在紫外灯下可发出强烈的黄色荧光。

图1 日光和紫外光下的CdTe量子点Fig.1 CdTe quantum dots in daylight and ultraviolet light

2.1.2 紫外-可见吸收光谱和荧光光谱 取适量量子点，分别进行紫外扫描分析和荧光光谱分析，其中荧光光谱的激发波长为380 nm，激发狭缝和发射狭缝均为5 nm。如图2所示分别为量子点的紫外吸收光谱（a）和荧光光谱（b），由图可知，量子点在较宽范围内有连续的吸收，最大吸收波长在520 nm左右，根据经验公式[7]：D=（9.812 7×10-7）λ3-（1.714 7×10-3）λ2+1.006 4λ-194.84（λ 为最大吸收波长），可计算出量子点尺寸约为2.81 nm。由荧光光谱可知，最大发射峰的位置在560 nm左右，半峰宽较窄，说明了所制备的量子点粒径分布范围比较小。

图2 为量子点的紫外可见吸收光谱和荧光光谱Fig.2 Absorption and fluorescence spectra of CdTe quantum dots

2.1.3 电镜图 本方法所制备的CdTe量子点形状呈类球状，尺寸较为均一且分散性良好，粒径大小也与根据经验公式所推算出的结果基本吻合，见图3透射电镜图。

图3 CdTe量子点的透射电镜图Fig.3 TEM image of CdTe QDs

2.2 偶联条件的优化

量子点与抗体的偶联效果会因偶联条件的不同而有所变化，本文中分别比较了不同pH、温度、时间及离子强度下，QDs-Ab的荧光发射光谱，从而选择最优的偶联条件。

2.2.1 pH 分别配制不同 pH 值（5.5，6.0，6.8，7.4，8.0，8.8，9.5）的 PBS溶液作为量子点与抗体偶联的反应体系，然后测量偶联物的荧光强度。如图4所示，当溶液pH值偏酸或偏碱性时，偶联物的荧光强度比较低，一方面可能是由于在不适宜的pH下量子点会出现荧光猝灭现象，另一方面是溶液的pH值会引起抗体的活性降低，使其与量子点的偶联率下降，削弱了它对量子点表面的包覆修饰作用，促使荧光强度的减小。当pH值为7.4时，抗体的活性最佳，与量子点的偶联率增加，荧光强度也达到最大值。

图4 酸碱度对偶联物荧光强度的影响Fig.4 Effect of pH on the fluorescence intensity of conjugates

2.2.2 温度和时间 在4，25，37℃，分别测定不同时间体系荧光强度的变化。如图5所示，在2 h之内的不同温度下，反应体系的荧光强度都在随着时间的延长而增加，其中，37℃的反应体系荧光强度要显著高于4℃和25℃的反应体系，这也是由于反应速度会随着温度的升高逐渐加快，荧光强度也就随之增大。但2 h之后，37℃的反应体系荧光强度开始下降，这是由于随着反应时间的延长，抗体的活性会逐渐下降，甚至最终会低于其他温度下的反应体系。但是考虑到抗体在37℃下活性较高，并且此温度下反应速度快，省时，所以最终选定的反应温度和时间为37℃、2 h。

图5 温度和反应时间对偶联物荧光强度的影响Fig.5 Effect of temperature and time on the fluorescence intensity of conjugates

2.2.3 离子强度 不同浓度氯化钠对QDs-Ab偶联物荧光强度的影响，如图6所示，少量氯化钠的加入可以抑制QDs-Ab形成静电双电层，减少静电排斥，从而增强QDs-Ab的活性。但过量的氯化钠会增强蛋白质的水合作用，同时抑制偶联物的亲和力[8]。所以本实验最终选择的氯化钠终浓度为0.2 mol/L。

图6 离子强度对偶联物荧光强度的影响Fig.6 Effect of quality of sodium chloride on the fluorescence intensity of conjugates

2.3 偶联结果的鉴定

2.3.1 偶联前后光谱的变化 量子点与抗体偶联前后的紫外吸收曲线并没有发生明显的位移，如图7（a）所示，说明偶联后量子点的大小和形貌并没有发生明显的改变，但偶联后的荧光强度略有增强（图7（b）），原因可能是抗体将量子点表面包覆后，对量子点的表面起到了钝化作用，有效去除量子点表面缺陷，降低了无辐射跃迁的几率[9]，使荧光强度有所提高。此外，由于量子点经EDC与抗体偶联之后，一个蛋白可能结合多个量子点，拉近量子点之间距离，导致量子点之间的偶极相互作用增强[10]，使其斯托克斯位移增大，荧光发射峰的峰位发生轻微的红移[11]。

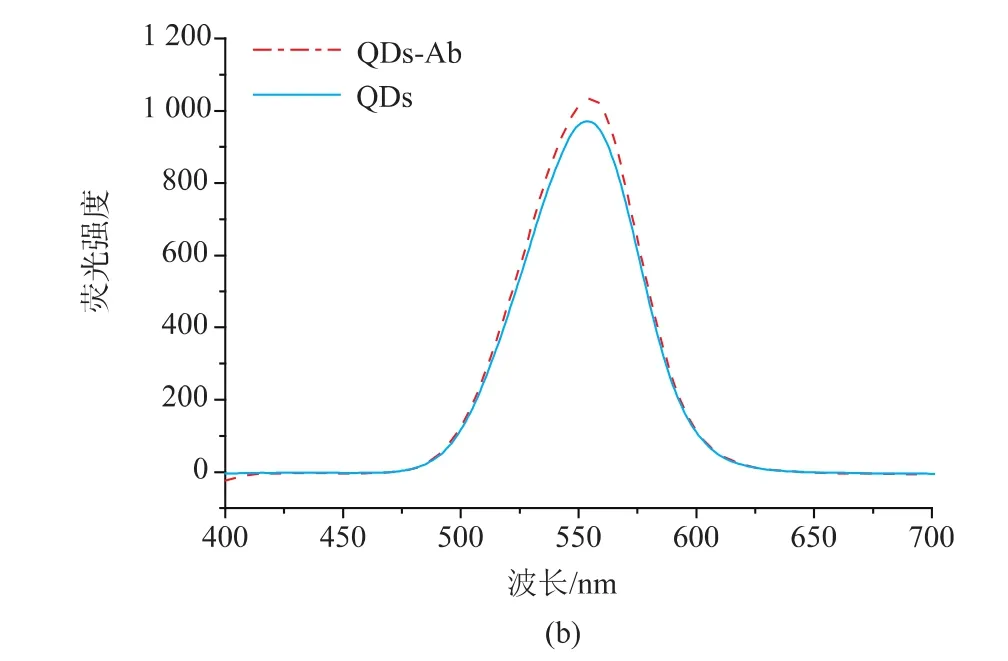
图7 量子点与量子点-抗体偶联物的紫外吸收光谱和荧光光谱Fig.7 Absorption spectrum and fluorescence spectrum of QDs and QDs-Ab

2.3.2 电泳鉴定 对QDs-Ab偶联物进行SDS-聚丙烯酰胺凝胶电泳，各道上样的样品及上样量分别是：1泳道为 10 μL标准蛋白 Marker，2泳道为 10 μL量子点，3泳道为10 μL微囊藻毒素抗体，4泳道为 10 μL QDs-Ab 偶联物，5 泳道为 20 μL QDs-Ab偶联物。电泳结束后，用凝胶成像仪对其进行透射拍照，获得图8（a）。然后将凝胶经过染色、脱色处理后，再用成像仪对凝胶再次进行拍照，获得图8（b）。

未标记的抗体（或Marker）不会产生荧光，透射拍照也就不会产生亮带。而量子点有荧光，所以在紫外照射下会有条带，如图8（a）所示，2、4、5 泳道都有亮光，并且QDs-Ab偶联物（4，5泳道）亮光的强度会随着上样量的增加而增强。在考马斯亮蓝染色之后，图8（b）中所示，QDs（2泳道）无条带，Marker，抗体及QDs-Ab均有明显的条带，表明QDs与Ab偶联成功。

图8 偶联物透射电泳图和偶联物照射电泳Fig.8 Transmission electrophoresis of QDs-Ab conjugations and the exposure electrophoresis of QDs-Ab conjugations

2.4 量子点与抗体相互作用的研究

2.4.1 量子点对抗体吸收光谱的研究 37℃（310 K）时，不同浓度的量子点（0，2×10-6，4×10-6，8×10-6，1×10-5，1.2×10-5，1.4×10-5，1.6×10-5，1.8×10-5，2×10-5mol/L）对抗体（浓度为1×10-5mol/L）吸收光谱的影响，如图9所示，抗体本身的吸收峰较宽，最大吸收峰值在280 nm左右，随着量子点浓度的增加，抗体的吸收峰逐渐增加，并发生轻微的蓝移（从280 nm移动至278 nm），这表明了抗体结构发生一定的变化，由于动态猝灭不会引起吸收光谱的变化[12]，因此可以进一步证明量子点与抗体之间的作用属于静态猝灭。除此之外，我们还可以依据公式（1）推算出量子点与抗体之间的表观结合常数Kapp[13]。

其中A，A0，Ac分别代表加入不同浓度量子点时，不含量子点时BSA的吸光度以及混合物的吸光度。根据公式（1），计算 1/（A-A0），并与 1/[QDs]，通过线性拟合，可以看出1/（A-A0）与量子点浓度的倒数呈线性关系（见图9 插图），其中斜率为 1/Kapp（Ac-A0），截距为 1/（Ac-A0），最终计算可知 Kapp大约为 3.37×104M-1（R2=0.990 6）

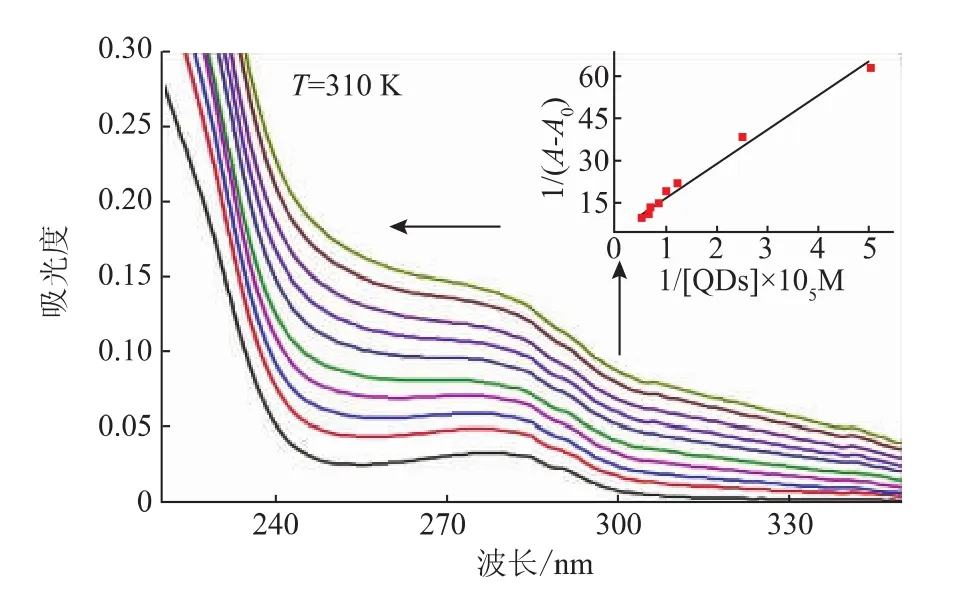
图9 加入不同浓度的CdTe量子点，抗体吸收光谱的改变（插图为1/（A-A0）与量子点浓度的线性关系）Fig.9 Absorption spectrum of antibody in the absence and presence of CdTe QDs at 310 K（The insert is the straight line dependence of 1/（A-A0） on the reciprocal concentration of CdTe QDs）

2.4.2 量子点对抗体荧光光谱的影响 荧光光谱是获得蛋白构象及动态变化的一种有效方法，众所周知，荧光猝灭通常是由2种因素引发的，一种由碰撞引起（动态猝灭），另外一种是猝灭剂与荧光物质形成复合物引起的（静态猝灭）[14]。因此我们通过研究QDs对抗体荧光光谱的影响可以判断引发荧光猝灭的类型，并能对猝灭机制有进一步的了解。如图10 所示，为不同温度下（a：298 K，b：304 K，c：310 K），量子点对抗体荧光光谱的影响，其中抗体浓度固定为 1×10-5mol/L，QDs浓度（从 A 到 I）分别为 0、8.0×10-6、1.6×10-5、2.0×10-5、4.0×10-5、6.0×10-5、8.0×10-5、1.0×10-4、1.2×10-4mol/L。如图所示，抗体的最大发射波长在340 nm左右，随着QDs浓度的增加，抗体的荧光强度显著下降，不同温度下，荧光强度的下降程度也有所不同，量子点对抗体荧光强度的猝灭，可通过Stern-Volmer公式进行计算[15]：

其中，F0，F分别代表没有QDs存在，以及有QDs存在时抗体的荧光强度；[Q]为量子点的浓度；KSV为Stern-Volmer猝灭常数。从图10插图可以看出，在量子点较低浓度范围内 （2×10-6～2×10-5mol/L），F0/F与浓度的关系与Stem-Volmer公式比较吻合。因此，在低浓度范围，将不同温度下F0/F与量子点的浓度进行线性拟合。

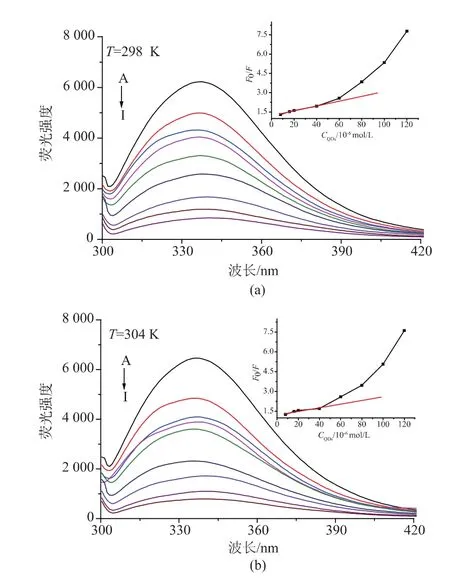
图10 不同温度下，加入不同浓度的量子点，抗体荧光光谱的变化 （插图为量子点溶液对抗体相对应的Stem-Volmer猝灭曲线）Fig.10 Fluorescence spectra of antibody in the presence of different concentrations of QDs at different temperature，and the inset corresponds to Stern-Volmer plots of the quenching of the fluorescence of antibody by QDs

如图11所示，为不同温度下，量子点对抗体荧光猝灭的Stem-Volmer曲线，结果表明，量子点对抗体荧光猝灭的Stem-Volmer曲线具有良好的线性关系，且该猝灭曲线与温度相关。表1列出了不同温度下的Stem-Volmer猝灭常数KSV，随着温度的升高，KSV反而会下降。由于动态猝灭依赖于扩散，而扩散系数会随着温度的升高而增加，因此动态猝灭常数一般也会随着温度的升高而增大，然而对于静态猝灭来说，形成的复合物的稳定性会随着温度的升高而下降，因此，静态猝灭常数就会与温度呈负相关[16]，所以进一步说明了量子点与抗体之间的相互作用属于静态猝灭，双分子猝灭公式如下：

式中，Kq为双分子速率常数，τ0为无猝灭剂时荧光物质的平均寿命，对于生物大分子，通常τ0=10-8S。根据公式（3）可计算出不同温度下的Kq，结果列于表1。荧光猝灭剂对生物大分子的扩散碰撞猝灭常数，最大时通常为1010M-1·S-1[17]，量子点对抗体猝灭实验所得的Kq远远大于扩散碰撞猝灭常数，结果也同样表明量子点对抗体的猝灭方式为静态猝灭。

由于前面的研究表明，量子点对抗体的猝灭机制为静态猝灭，因此需要用修正的 Stem-Volmer公式（4）来计算猝灭参数[12]。

其中，△F为猝灭剂（量子点）不存在时和存在时，抗体荧光强度的差值；fa为可被荧光猝灭剂接近的发色基团的摩尔百分比；[QDs]为量子点的浓度；Ka为有效猝灭常数。以F0/△F与1/[QDs]作图（图12所示），经线性拟合后，斜率为 1/（faKa），截距为 1/fa，不同温度下的Ka的计算结果列于表1，结果表明Ka也会随温度的的升高而下降，这一变化趋势与KSV一致，这一特性符合静态猝灭机制。

图11 不同温度下，量子点溶液对抗体的Stem-Volmer猝灭曲线（插图为Stern-Volmer猝灭常数KSV与温度的关系）Fig.11 Stern-Volmer plots for the quenching of antibody by QDs at different temperatures.The inset shows the relationship of the Stern-Volmer quenching constants KSVand temperature

表1 不同温度下，CdTe量子点溶液与抗体相互作用的Stem-Volmer公式和修正的Stem-Volmer公式的猝灭常数Table 1 Stern-Volmer and modified Stern-Volmer quenching constantsoftheQDs-antibody system at different temperatures

图12 不同温度下，量子点溶液对抗体的修正的Stem-Volmer猝灭曲线（插图为修正的Stern-Volmer猝灭常数Ka与温度的关系）Fig.12 Modified Stern-Volmer plots for the quenching of antibody by QDs at different temperatures.The inset shows the relationship of the modified Stern-Volmer quenching constants Kaand temperature

2.4.3 结合位点n和结合常数K 由于量子点对抗体的荧光猝灭属于静态猝灭，因此，它们之间应该存在结合位点，之前的研究，结合位点可以通过公式（5）来进行计算[18]

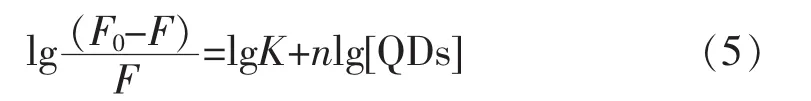
其中，K是结合常数；n为结合位点的个数。以lg[（F0-F）/F]与 lg[QDs]作图（图10 所示），通过线性拟合，可以得到不同温度下的结合常数K和结合位点n，计算结果列于表2，结果表明随着温度的升高，结合常数K会不断减小，和修正的Stem-Volmer猝灭常数Ka有相同的变化趋势。由于有效猝灭常数Ka可以近似的认为是猝灭剂和受体体系中的表观结合常数[19]。将结合常数K的值和表观结合常数的值相比较发现，结合常数均在同一个数量级上，因此，可以断定量子点和抗体之间的结合常数约104M-1[20]。此外，我们发现不同温度下量子点和抗体的结合位点均接近于1，表明两者仅有一个结合位点。

2.4.4 热力学常数△H，△G和△S 通常，内源性或外源性配体与生物大分子之间的作用力包括静电相互作用、氢键、范德华力、疏水相互作用等。为了进一步研究量子点与抗体之间的作用，我们需要了解两者之间作用的热力学参数△H，△S和△G。其中焓变（△H）是反应过程中分子内键能交换的结果；熵变（△S）是反应体系中混乱度变化的指标；自由能（△G）的变化可以判断反应是否自发进行。

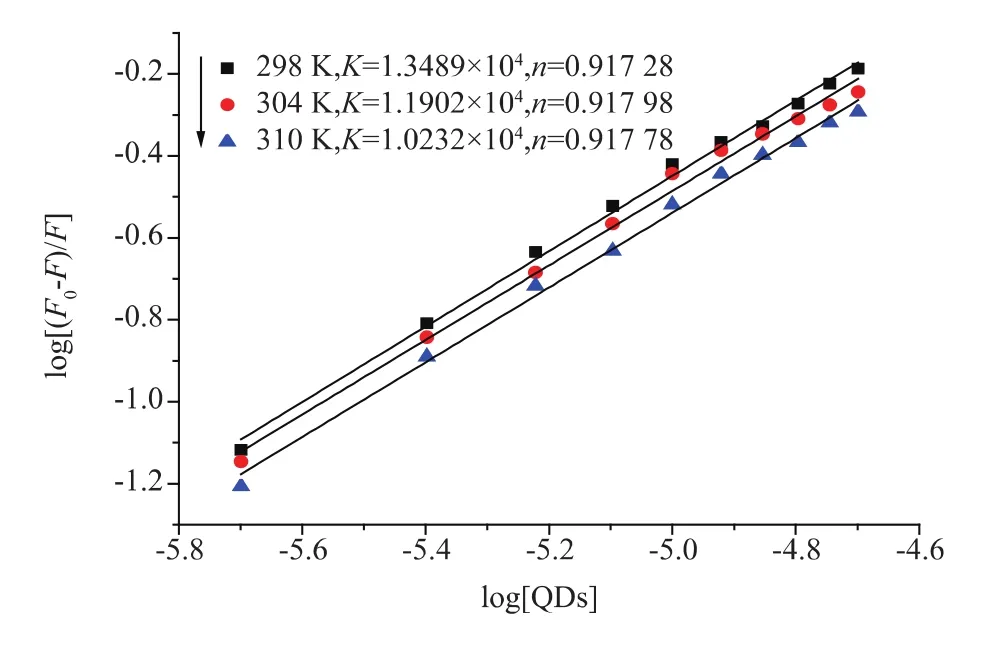
图13 不同温度下，量子点溶液与抗体相互作用时log[（F0-F）/F]对 log[QDs]时的曲线Fig.13 Plot of log [（F0-F）/F]versus log [QDs]for antibody with QDs at different temperature

在实验温度范围内，△H受温度影响不大，则△H和△S我们可以通过van’t Hoff公式（6）出计算热力学常数

其中，K为结合常数；△H，△S分别代表反应的标准焓变和熵变；R 为气体常数 （8.314 J/（mol·K））；T为温度（单位为K）。如图14所示，lnK与1/T具有良好的线性关系，R2=0.997 78，△H和△S可通过斜率和截距求得，自由能△G可根据公式（7）进行计算，计算结果全部列于表2中，

图14 量子点与抗体相互作用的Van't Hoff关系图Fig.14 Van't Hoff plots of QDs-antibody system

之前的研究表明[21]疏水作用会对体系的△H＞0和△S＞0产生贡献，△H＜0，则反应主要为静电作用，△S＜0，起主要作用的可能是氢键和范德华力，如表2所示，在不同温度下，△G＜0，表明量子点与抗体的结合是自发进行的，△H（＜0）和△S（＞0）表明在这个结合反应中，量子点与抗体之间的作用力是静电相互作用为主，此外氢键、范德华力也会起一定的作用。

表2 不同温度下，量子点溶液与抗体相互作用的结合常数、结合位点数及热力学参数Table 2 Thermodynamic parameters and the number of binding sitesofQDs-antibody atdifferent temperatures

3 结语

试验优化了荧光探针的制备条件，结果表明在pH为7.4，37℃反应2 h，离子浓度为0.2 mol/L时，制备的荧光探针效果最好，然后通过电泳对偶联结果进行鉴定。此外，选取298 K、304 K、310 K作为实验条件，对量子点与抗体的相互作用进行了深入的研究，根据公式（1—7），可以分别得到量子点与抗体的表观结合常数Kapp，荧光猝灭常数KSV，结合常数K，结合位点n，以及热力学参数△H（＜0）△G（＜0）△S（＞0）等，结果表明，量子点对抗体具有荧光猝灭作用，猝灭方式属于静态猝灭，即量子点是与抗体形成某种特定结构的配合物而引起的荧光猝灭。量子点与抗体的结合起主要作用的是静电相互作用，同时氢键、范德华力也会起一定的作用。

随着量子点的应用越来越广泛，如何实现量子点与抗体等物质的偶联，同时还能保持它们的生物活性，也是推动量子点在生物标记，免疫学检测等方面应用的一个重要环节，通过本文作者这一系列的研究，我们对量子点与抗体之间的作用有了更深入的了解，这也为荧光探针的制备以及量子点在免疫学方面的应用提供一些理论支持。