削弱震荡节点的LDPC码译码算法研究

陈紫强 王广耀

(1. 桂林电子科技大学,广西桂林 541004； 2. 桂林电子科技大学信息与通信学院,广西桂林 541004)

1 引言

低密度奇偶校验(Low-Density Parity-Check)码是误码性能最接近香农极限的线性分组纠错码[1]。近年来,低复杂度、高性能的LDPC码译码算法成为国内外研究的热点[2- 6]。文献[2]提出的置信传播(belief propagation,BP)算法误码性能极好,但译码复杂度较高,不利于硬件实现。Elidan提出基于残差值的置信传播算法[3](Residual Belief-Propagation,RBP),根据节点更新前后消息的残差值来进行选择更新,优先更新残差值最大的节点,使其接收更多的外信息,从而加快收敛速度。然而,在每次迭代中都要对消息更新前后的残差值进行比较排序,确定消息的更新次序,因此在加快收敛速度的同时也会出现“贪婪性”问题,导致已经正确译码的比特节点在译码更新处理中再次出错。文献[4]对RBP算法作进一步改进,提出了一种基于变量节点信息的译码算法(Variable-to-Check RBP,VC-RBP),仿真结果表明,该算法较RBP算法有着约0.3 dB的性能提升,且复杂度也有所降低。文献[5]简化了RBP算法剩余信息的计算公式,提出了一种复杂度更低,性能更好的校验节点信息动态策略分层BP算法。面向节点的残差置信传播算法(Node-Wise RBP,NW-RBP)[6]利用最大残差值对节点进行更新排序,首先更新完该节点的相邻边,然后再进行判决,让更多不可靠的变量节点接收外信息,从而改善贪婪性,但是该算法增加了译码复杂度,并且误码性能有待进一步提高。

鉴于此,提出了基于变量节点消息震荡现象的残差置信传播(VNO-RBP)算法。该算法采用先分组后选择的动态调度思想,以相对残差值为参考指标,优先更新残差值较大的节点,加快译码收敛；同时,对于译码过程中出现的震荡节点前后两次迭代中的LLR值作加权平均处理,提高该节点的可靠度；然后继续进行下一轮迭代。理论分析和实验仿真证明了本文提出的VNO-RBP算法的译码复杂度更低,并且误码性能优于NW-RBP算法。

2 VNO-RBP译码算法

NW-RBP算法通过让不可靠的变量节点获得更多的外信息,降低了RBP算法的贪婪性。然而该算法选择标准单一,使得优先传递不可靠变量节点并不能降低该节点的不可靠度。在消息传递过程中,前后两次迭代之间的变量节点LLR值可能会发生大幅震荡,称之为震荡现象[7]。对于这类节点即使优先更新,也不一定能够消除震荡现象。本文在动态调度算法的基础上先引入停止准则,然后设计一种震荡节点消息处理方案,以降低震荡节点对相邻节点可靠度的影响。

2.1 停止准则

停止准则主要应用于多步译码通信领域。在译码迭代消息达到特定条件时停止当前译码,结束译码或者继续进行下一步译码[8]。VNO-RBP算法通过分析迭代次数与错误节点个数的关系来确定基本的停止准则。图1为(864,432)QC-LDPC码[9]在不同信噪比下进行Log-BP译码时迭代次数与错误节点个数的关系图。仿真条件：AWGN信道下经由BPSK调制,最大译码迭代次数为50次。从图1中可以看出,在一定范围内,随着迭代次数的增长,错误节点个数迅速减少。但当迭代次数增加到一定程度时,错误节点个数出现震荡现象,导致译码消息难以收敛。我们根据这个特征来设置停止准则,使用β作为Log-BP译码的第一步迭代次数,若迭代β次仍无法全部译码成功,则进行动态调度译码算法的第二步。根据图1中译码迭代次数与错误节点个数的关系,我们令β=3。译码的基本流程如下：

(1)使用Log-BP算法进行迭代译码；

(2)迭代3次后,如果译码迭代消息满足停止准则,则跳至下一步；如果译码成功则结束译码；

(3)使用动态调度策略选择优先更新的节点；

(4)优先更新相对残差值较大的节点并对更新后的节点信息作震荡处理,然后重新选取优先更新的节点进行下一次迭代；

(5)结合变量节点的后验LLR值对该节点进行译码判决；

(6)计算伴随式的值,若结果为0或达到最大迭代次数,则结束译码,否则跳回第3步继续迭代。

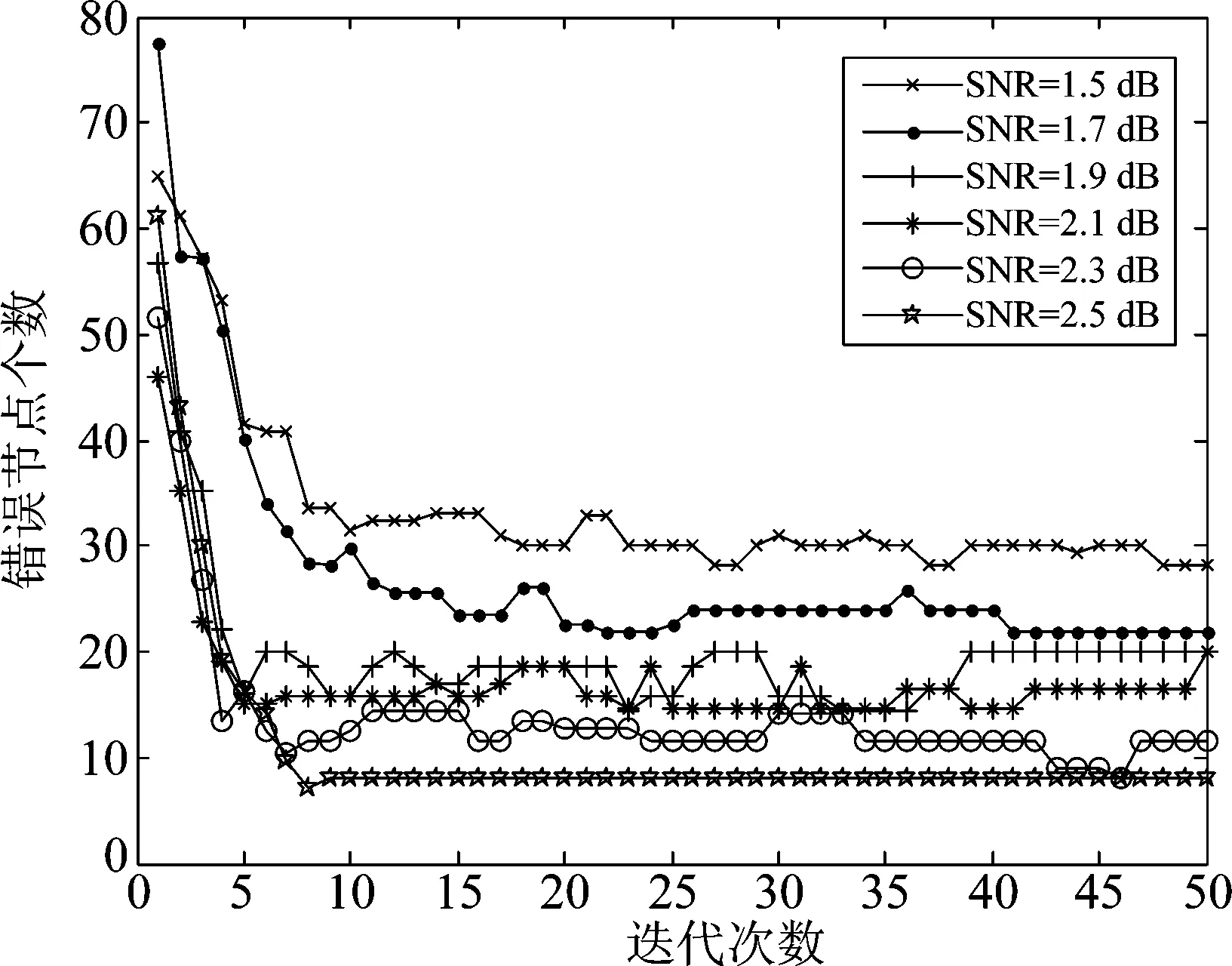
图1 不同迭代次数下错误节点个数的变化

2.2 动态调度策略

动态调度策略的主要思想就是根据一定的规则选择优先更新的节点,然后采用Log-BP算法对选定的边进行更新。因此在动态调度算法中,边的选择策略直接影响着最终的误码性能[10]。由于本文的动态调度是基于Log-BP算法进行改进的,我们首先分析Log-BP算法的特点：

(1)在Log-BP译码过程中,部分变量节点只需要很少的迭代次数就拥有较高可靠度,不再产生震荡。

(2)当译码消息收敛时,节点处更新前后的数值基本不变。

(3)节点处更新前后的数值相差很大时,说明译码消息没有收敛。

(4)译码过程中,即使进行了多次迭代,依然存在震荡现象。

动态调度策略就是利用上述特点,根据一定的规则选择优先更新的节点。在现有的动态调度算法中,普遍以残差值来决定变量节点的优先更新顺序,最大残差值代表该节点最不可靠,在译码中拥有最大优先权[11]。但是这种单一的判断指标并不具备完整性,事实上,最大残差值并不意味着该处的变量节点绝对是最不稳定的[12]。

本文提出的动态调度策略不再以最大残差值作为决定节点是否优先更新的指标,而是首先对变量节点进行分组,然后使用相对残差值rr(mc→ν)来进行判定

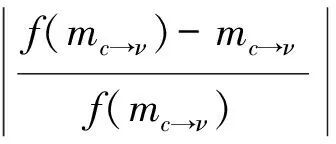
(1)

其中,mc→ν为从校验节点c传递到变量节点ν的信息,f(mc→ν)表示mc→ν更新后的值。当节点处的相对残差值趋向于0时,说明该节点的译码消息收敛；反之当相对残差值较大时,说明该消息难以收敛。优先更新最大相对残差值对应的节点,会加快译码收敛速度。

对变量节点的分组采用如下策略：首先对于所有的变量节点,将前后两次迭代中消息符号发生改变的变量节点集合记为S,其余变量节点集合记为C。其次,定义S1为S中满足|mi|>|f(mi)|的节点集合,S2为S中满足|mi|<=|f(mi)|的所有节点集合,其中mi为变量节点νi的信息,f(mi)表示mi更新后的信息。最后将三组集合分别按照相对残差值大小排序,具体优先级如下：

(1)如果S1不为空集,选择S1中对应相对残差值最大的节点优先更新；

(2)如果S1为空集、S2不为空集,选择S2中对应相对残差值最大的节点优先更新；

(3)如果S为空集、C不为空集,选择C中对应相对残差值最大的节点优先更新。

2.3 震荡节点的处理

变量节点消息更新：

L(l)(νij)=L(pi)+∑j′∈N(i)jL(l)(cj′i)

(2)

译码判决：

L(l)(νi)=L(pi)+∑j∈N(i)L(l)(cji)

(3)

假设某一变量节点的度数为dν,则由式(2)和式(3)可以得到：

(4)

其中,L(l)(νij)为该变量节点在第l次迭代中的LLR值,L(l)(νi)为该变量节点在第l次迭代中的译码判决消息值,L(pi)为该变量节点的先验消息。由式(4)可发现,变量节点伪后验概率L(l)(νi)会随着其LLR值的震荡而出现无法收敛的情况,这势必会导致译码的错误判决。因此对震荡节点的LLR值进行修正,能够及时纠正消息传递中的错误消息的传播,达到改善译码性能的目的。

一般错误比特数和震荡节点个数同时变化,错误节点的LLR值很小且符号频繁变化[13]。当某一变量节点的LLR值在相邻两次迭代过程中符号发生变化时,前后两个LLR值之间必有一个是趋于正确的[14-15]。用二者的均值来替代该节点第l次迭代之后的LLR值,可以降低前后两次迭代变量节点LLR值的变化幅度,增加收敛到正确码字的可能性。这种处理方案虽然不能完全消除变量节点LLR值的震荡现象,但可以减少震荡节点的数目,避免震荡节点LLR值的传播干扰其他节点的正确译码；从工程实现的角度分析,只需增加一个缓存器用于存储上一次迭代中的变量节点外部LLR值,以及一个除法器用于将加权后的信息右移一位以得到变量节点的更新值,无需任何乘法器,付出的硬件资源代价很小。

在动态调度策略选中的节点中,将震荡节点前后两次迭代中的外部LLR值作均值处理。如果一个节点多次震荡,那么它会被多次处理,直至节点的震荡越来越小。如图2所示,采用IEEE802.16e标准中的(864,432)QC-LDPC码进行传统的Log-BP译码,假设采用全零码字传输。对变量节点的外部LLR值作均值处理后,错误节点数明显有所减少,证明了均值处理方案的有效性。处理方式如下：

(5)

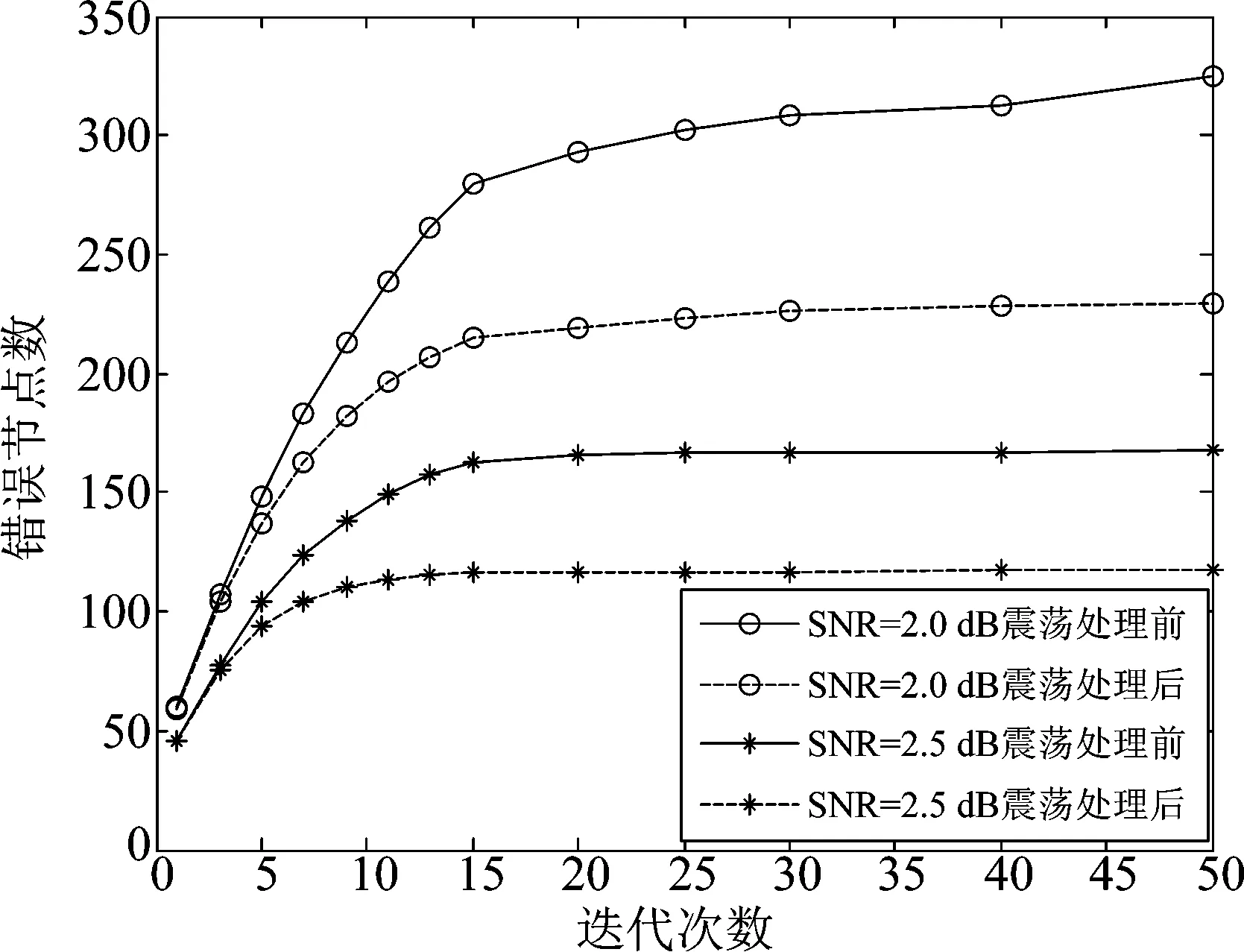
图2 均值处理前后的错误节点数目对比

2.4 VNO-RBP算法流程

在VNO-RBP译码算法中,首先进行第一步译码并迭代3次。如果满足停止准则,则进入下一步译码。第二部分的译码主要包括动态调度策略和震荡节点外部消息的取均值处理,首先对所有变量节点按照既定的调度策略选择最不可靠的变量节点νi。然后更新所有与该节点相连接的校验节点。判断变量节点νi更新前后的取值是否需要进行处理。更新相应的变量节点消息,并计算后验消息。其中,mcν为信道初始消息,R(j)和C(i)分别表示校验节点cj及变量节点νi的相邻节点,用mcj→νi表示cj传递到νi的信息,用mνi→cj表示νi传递到cj的信息,其余符号参照Log-BP译码算法。具体的算法流程如下：

LDPC码VNO-RBP译码算法流程1. 初始化mcν=0 2. 初始化mνi→cj=2yi/σ2 3. for 任意cj4. for 任意νi∈R(j)5. 计算mcj→νi6. end for7. end for8. for 任意νi9. 计算L(νi)与相对残差值rr(mνi→cj) 10. end for11. 根据所提的节点分组策略选择νi12. for 任意νi∈R(j)i13. 产生并传递mcj→νi14. end for15. 计算硬判决消息L(νi)

16. 判断是否取均值处理17. 置rr(mνi→cj)=0 18. for 任意cj∈C(i)j19. 产生和传递mνi→cj20. end for21. if 不满足停止准则22. 返回到第3行23. end if

3 仿真结果与性能分析

为了验证本文所提算法性能的有效性,仿真分别采用IEEE802.16e标准码中码长为864,码率为0.5的QC-LDPC码,简称C1；以及码长为1056,码率为0.5的Mackay码[16],简称C2。在AWGN信道下采用BPSK调制,设置最小误帧数为10帧,最大译码迭代次数为50次,分别对Log-BP算法、NW-RBP算法以及VNO-RBP算法的误码性能进行仿真比较。

从图3、图4中可以看出,本文提出的VNO-RBP算法的误码性能明显优于其他两种算法。在码C1条件下,当信噪比为3.5 dB时,VNO-RBP算法与Log-BP算法相比,误码率由10-4量级降到10-5量级,同时与NW-RBP算法相比,性能提升约0.31 dB。在码C2条件下,当信噪比为2.5 dB时,VNO-RBP算法与Log-BP算法相比误码率由10-4量级降到10-5量级,与NW-RBP算法相比也有一定程度上的性能提升。主要是由于VNO-RBP算法优先选择相对残差值较大的节点进行更新以及对不可靠节点进行震荡处理,从而提高译码性能。

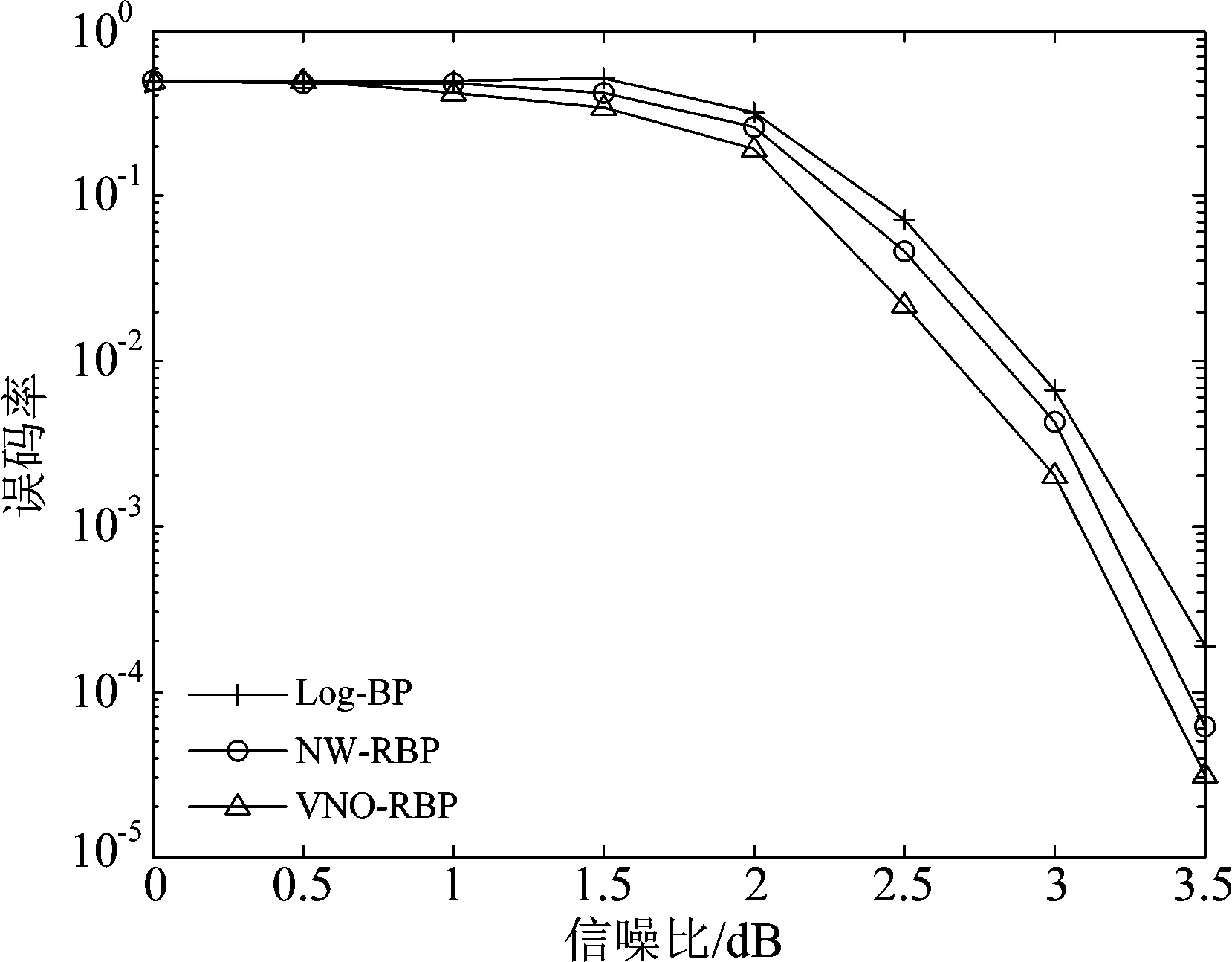
图3 码C1条件下的误码性能比较

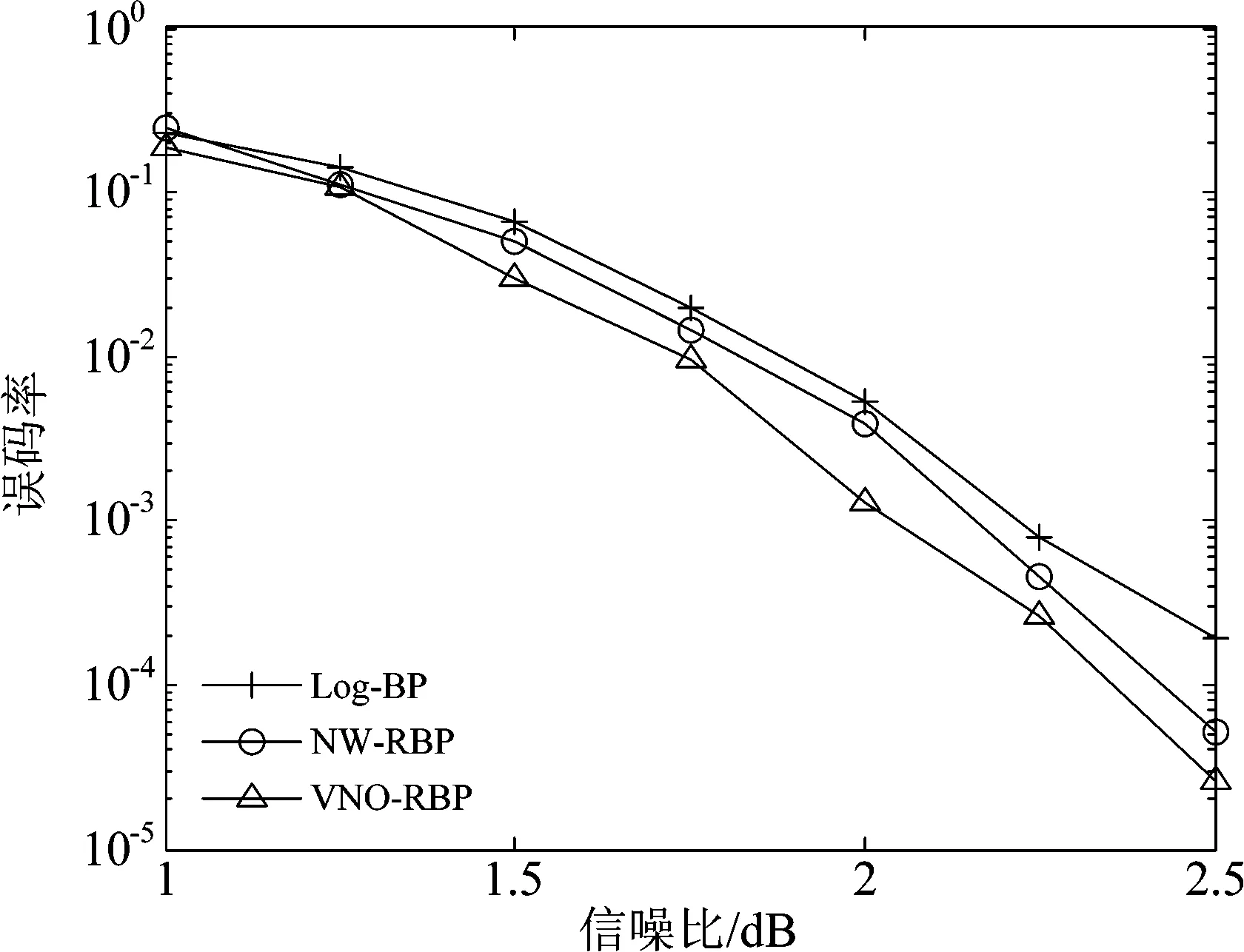
图4 码C2条件下的误码性能比较

对于码C1,当误码率为10-5时,分别对Log-BP,NW-RBP和VNO-RBP算法的平均迭代次数进行比较分析,如表1所示。

表1 不同译码算法的平均迭代次数

由表1可得,与Log-BP,NW-RBP算法相比,VNO-RBP算法的平均译码迭代次数减少了55.2%和38.1%,明显地加快了收敛速度。原因为VNO-RBP算法在变量节点迭代更新过程中优先更新相对残差值较大的节点,且对震荡节点的LLR值进行了加权处理,减少震荡节点数目,从而促进译码正确节点LLR值的传递,达到降低译码迭代次数的目的。

4 复杂性分析

对于规则LDPC码,假设校验矩阵H为M行N列,dc与dν都是固定的,dc为校验节点的度数,dν为变量节点的度数。令Log-BP算法中节点更新计算量E=dc*M=dν*N,表2以此为基准表示出不同译码算法在一次迭代中的计算量。

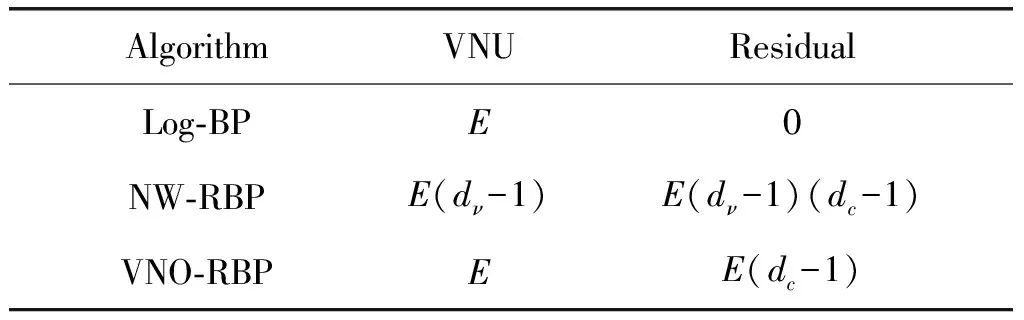
表2 不同译码算法的运算复杂度

从表1可以看出,Log-BP算法总体复杂度最低,NW-RBP的运算量最大,VNO-RBP算法复杂度介于二者之间。其中VNU列代表变量节点更新的计算量,Residual列代表计算残差值所需要的计算量,3种算法的校验节点更新计算量均为E。以(3,6)LDPC码为例,VNO-RBP的计算量比NW-RBP减少约6E,因此本文所提的VNO-RBP算法在一定程度上降低了NW-RBP译码算法的复杂度。

5 结论

为了进一步降低NW-RBP算法的误比特率,提出一种基于变量节点消息震荡的残差置信传播算法。采用新的动态调度策略,首先对变量节点进行分组,然后优先更新相对残差值较大的变量节点,加快译码收敛速度。同时对相邻两次迭代中发生震荡变量节点的外部信息进行加权平均处理,降低该变量节点的不可靠性。实验仿真和理论分析表明,本文所提的VNO-RBP算法的误码性能明显优于NW-RBP算法,同时复杂度也有所降低。

[1] Varnica N, Burd G, Gunnam K. Optimizing error floor performance of finite-precision layered decoders of low-density parity-check (LDPC) codes: US, US 8291292 B1[P]. 2012.

[2] Sibel J C, Crussiere M, Helard J F. Modeling BP decoding error events with the LDPC codes of the DVB-S2 standard[C]∥IEEE, International Symposium on Personal, Indoor, and Mobile Radio Communication. IEEE, 2014:902-907.

[3] Saha S, Hussain S R, Rahman A K M A. RBP: Reliable Broadcasting Protocol in Large Scale Mobile Ad Hoc Networks[C]∥IEEE International Conference on Advanced Information NETWORKING and Applications. IEEE Computer Society, 2010:526-532.

[4] Kim J H, Nam M Y, Song H Y, et al.Variable-to-Check Residual Belief Propagation for informed dynamic scheduling of LDPC codes[C]∥International Symposium on Information Theory and ITS Applications. IEEE Xplore, 2008:1- 4.

[5] Han G, Liu X. An efficient dynamic schedule for layered belief-propagation decoding of LDPC codes[J]. IEEE Communications Letters, 2009, 13(12):950-952.

[6] Zhou H, Li P, Feng J, et al. Floodingand node-wise RBP sequentially concatenated decoder for LDPC codes[C]∥Ieee/cic International Conference on Communications in China. IEEE, 2015:1- 4.

[7] Hera A, Boncalo O, Gavriliu C E, et al. Analysis and implementation of on-the-fly stopping criteria for layered QC LDPC decoders[C]∥2015 22nd International Conference Mixed Design of Integrated Circuits & Systems (MIXDES), Torun, 2015: 287-291.

[8] Bian Y, Wang Y, Wang J. Lowering the Error Floor of LDPC Codes by a Two-stage Hybrid Decoding Algorithm[C]∥International Conference on Communications and NETWORKING in China, 2007. Chinacom. IEEE, 2007:590-594.

[9] 安永宁.基于IEEE802.16e标准的码率兼容QC-LDPC编译码器的FPGA实现[D].西安：西安电子科技大学,2014.

An Y Q.FPGA implementation of rate-compatible QC-LDPC codec based on IEEE802.16e standard[D]. Xi’an: Xidian University,2014.(in Chinese)

[10]Qiu N, Chen W, Lu Y, et al. Informed dynamic scheduling for majority-logic decoding of non-binary LDPC codes[C]∥GLOBECOM 2013-2013 IEEE Global Communications Conference, 2013:1874-1878.

[11]Liu X, Jamalipour A. Informed dynamic scheduling strategies for novel majority-logic decoding of non-binary LDPC codes[C]∥2015 9th International Conference on Signal Processing and Communication Systems (ICSPCS), Cairns, QLD, 2015: 1- 6.

[12]Mhaske S, Uliana D, Kee H, et al. A2.48Gb/s FPGA-based QC-LDPC decoder: An algorithmic compiler implementation[C]∥Sarnoff Symposium. IEEE,2015:88-93.

[13]Shin B, Park H, No J S, et al. Multi-Stage Decoding Scheme with Post-Processing for LDPC Codes to Lower the Error Floors[J]. Ieice Transactions on Communications, 2011, 94-B(8):2375-2377.

[14]Gounai S. Decoding Algorithms Based on Oscillation for Low-Density Parity Check Codes[J]. Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences, 2005, E88-A(8):2216-2226.

[15]Liu X, Zhang Y, Cui R. Variable-Node-Based Dynamic Scheduling Strategy for Belief-Propagation Decoding of LDPC Codes[J]. IEEE Communications Letters, 2015, 19(2):147-150.

[16]Mackay D J C. Good Error-Correcting Codes based on Very Sparse Matrices[J]. IEEE Transactions on Information Theory, 1999, 45(2):399- 431.