倒谱与相位模糊条件下的卷积码高容错识别
王伟年 彭 华 冀 磊
(解放军信息工程大学,河南郑州 450002)
1 引言
在数字通信系统中,纠错编码被广泛应用。在非合作通信领域,接收方需要根据接收到的比特流识别出编码方式,才能进一步得到有价值的信息,这就必然要用到信道编码分析技术[1]。而卷积码在实际环境中应用十分广泛[2],对其进行识别分析具有重要意义。但对于通信中的非合作方来说,信号接收设备的不一致,常常会导致接收的解调数据存在倒谱和相位模糊现象[3]。倒谱现象会造成符号的虚部取反,相位模糊则会造成符号旋转相应的度数,这无疑对信道编码分析技术提出了更高的要求。
目前与卷积码识别相关文献较多,总体上可以分为两类方法:利用硬判决数据的传统分析方法与利用软判决数据的新型分析方法。传统分析方法主要包括基于矩阵秩亏损算法[4-5]、基于欧几里得及其改进算法[6-7]、基于矩阵化简综合分析算法[8]等代数类方法和基于校验关系成立概率的穷举类方法[9-10]。代数类方法虽然计算复杂度较低,但抗误码能力较弱,不能适应低信噪比下的实际信号;穷举类方法虽然计算复杂度稍高,但应用于低码率卷积码识别时完全在可接受范围之内,且抗误码能力较强,能够适应复杂多变的实际信道。新型分析方法主要有文献[11-14]:文献[11]提出了校验方程成立的对数似然比(LLR)概念,将软判决数据应用于编码识别,提高了识别性能;文献[14]提出了似然差(LD)概念,并将似然差和BCJR译码分别应用于卷积码识别,前者与LLR方法相比降低了计算复杂度,且性能相当,后者大大提高了识别性能,但计算复杂度较高;文献[12]提出了基于Gibbs采样的卷积码识别算法,首次将实数域信号处理方法应用于信道编码识别,且具有较好的容错能力;文献[13]提出了基于编码系数代价函数优化求解的卷积码参数估计算法,提高了识别性能的同时降低了计算复杂度。
但上述文献都是假设接收数据中仅仅存在误码,鲜有文献涉及倒谱和相位模糊条件下的卷积码识别。实际通信中解决此问题的常规方法是遍历数据的各种情况并进行译码,根据译码结果判断倒谱及相位模糊的具体情况,但这无疑会大大降低通信效率。为解决此问题,本文提出了一种容错能力较强的倒谱和相位模糊条件下卷积码识别算法。首先推导了QPSK调制方式下符号信息到比特对数似然比信息的转换关系;然后提出一种校验向量的通用求解算法,利用该算法求得了各个条件下的校验向量;最后,利用三种方法测试了所得校验向量的识别效果。接下来的内容安排如下:第2节对倒谱及相位模糊条件下卷积码识别问题进行描述;第3节对卷积码识别数学模型进行介绍;第4节给出校验向量的求解过程及其在卷积码识别过程中的三种应用方法(WHT、LLR、LD);仿真实验结果在第5节中展示;末节将进行一些总结和讨论。
2 问题描述
本节描述倒谱及相位模糊条件下的卷积码识别问题。
实际通信系统部分模型如图1所示。本文重点研究倒谱与相位模糊条件下的卷积码识别,模型选取了比较典型的QPSK映射方式。另外,模型中信道为加性高斯白噪声信道。即:信息序列m经过卷积编码后得到编码序列c,编码序列c经过QPSK映射、调制以及高斯白噪声信道得到发送序列s,最后接收方对发送序列s进行解调得到存在噪声的符号序列r。
正常通信过程只需要将符号序列r进行解映射便可得到编码比特流,再进行卷积译码可以进一步得到信息序列。而对于通信中的非合作方,信号收发装置不匹配会导致倒谱和相位模糊现象产生,对应的解调比特流会发生颠倒、取反以及更复杂的变化,因此不能直接利用符号序列r解映射的比特流进行译码,必须先识别出是否存在倒谱和相位模糊,去掉此类影响后才能进行译码得到正确信息序列。本文所研究的内容便是在已知发送方卷积编码集合的基础上,仅利用解调符号序列(无特殊码辅助)识别出编码方式和可能存在的倒谱及相位模糊,保证译码结果的正确性。
在QPSK映射条件下,假设有p种卷积编码,每种卷积编码有q种删除模式,考虑到相位模糊(4种)以及倒谱(2种),总共可以得到校验向量8pq种(假设每种卷积码只有1个校验向量),本文所解决的问题便是如何快速求得8pq种校验向量以及如何利用这些校验向量快速识别出编码方式和可能存在的倒谱及相位模糊。

图1 通信系统部分模型
由于本文的映射方式是QPSK映射,符号序列r中每个符号代表两比特,而实际的卷积码识别分析工作必须在比特域中进行,因此必须首先将符号序列r转化到比特软信息序列y和硬判决01序列v,下面具体分析符号序列到比特软信息序列和硬判决01序列的转化过程。
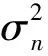
(1)
假设发送符号先验等概,由贝叶斯公式,可得ck中某比特的后验对数似然比概率如下式
(2)
又因为ck∈{βj},αj与βj存在一一映射的关系,所以式(2)可转化为下式
(3)
将式(1)带入式(3),可以简化得到下式
(4)
通过式(4)可以将符号序列r转化到比特软信息序列y,进一步可以硬判决得到比特01序列v。
3 卷积码识别数学模型
一般卷积码都有三个重要参数(n,k,d),n为码长,k为信息长,d为编码器存储深度(编码约束度),这些参数代表每一时刻输入k个信息比特,输出n个编码比特。除此之外,卷积码的生成多项式矩阵也尤为重要,可表示为下式:
(5)

令μi代表第i个输入的记忆长度,则有以下两式成立:
(6)
(7)

记要发送的二进制序列m=(m1,m2,m3,…)的多项式表示为m(D)=m1+m2D1+m3D2+…,其中mi∈GF(2);以k为周期将序列m拆分为k路序列,每一路序列用多项式mi(D)表示,则可得到拆分后的k维多项式向量为m(D)=(m1(D),…,mk(D)),其中mi(D)=mi+mk+iD1+m2k+iD2+…,i=1,…,k。对于上述参数的卷积码,编码过程可用下式表示:
c(D)=m(D)·G(D)=[c1(D),…,cn(D)]
(8)
其中c(D)代表输出编码多项式向量,大小为1×n,ci(D)是第i路输出序列的多项式表示。
令r=n-k,对于该卷积码,必定存在r×n阶的奇偶校验多项式矩阵H(D),使得下式成立
c(D)·HT(D)=G(D)·HT(D)=0
(9)
(10)
设H(D)中校验多项式的最高次数为正整数d′,则H(D)中每个元素均可表示为如下形式
(∀i=1,…,r;∀j=1,…,n)
(11)

(12)
其中A代表由码字构成的系数矩阵,B代表校验向量矩阵。
卷积码识别按照码字集合是否已知分为开集识别和闭集识别。开集识别就是在码集合未知的情况下,仅根据编码序列c求得H(D),进一步通过式(9)求得G(D),得到卷积码编码结构,进行正确译码得到原始信息;闭集识别则是在已知码集合的基础上,利用编码序列与校验向量的正交关系,直接判断出接收序列的编码方式。而本文则是在倒谱和相位模糊条件下,已知所有卷积码集合的基础上,完成卷积码的闭集识别,判断出接收数据的编码结构、是否存在倒谱以及相位模糊。
简单起见,这里重点研究实际应用较多的(2,1,d)卷积码及其删除码,对于更一般的卷积码,本文所提的校验向量求解算法以及采用的识别算法仍然适用,只是当该卷积码的校验向量不止一种时,需要取校验向量的一组基并对其进行综合利用。对于(2,1,d)卷积码,其生成多项式矩阵为G(D)=[g1(D),g2(D)],奇偶校验多项式矩阵为H(D)=[h1(D),h2(D)],编码多项式向量c(D)=[c1(D),c2(D)],则式(9)可简化为
c1(D)h1(D)+c2(D)h2(D)=
g1(D)h1(D)+g2(D)h2(D)=0
(13)
求解得到
(14)
同时式(12)化简为
[h1,d′,h2,d′,h1,d′-1,h2,d′-1,…,h1,0,h2,0]T=0
(15)
由式(15)可求得对应于编码序列c的校验向量h=(h1,d′,h2,d′,h1,d′-1,h2,d′-1,…,h1,0,h2,0),下文对卷积码的识别过程均基于该校验向量。
4 校验向量求解及应用
由第3节可知,校验向量在卷积码识别过程中有着至关重要的作用。为了更加系统、快速地完成卷积码闭集识别工作,本节将对卷积码数据各种条件下的校验向量如何求解进行详细介绍,并在此基础上介绍校验向量应用于卷积码识别的三种方法,最后对三种方法的计算复杂度进行分析。
4.1 校验向量求解
本小节将对各种码率、倒谱及相位模糊条件下卷积码的校验向量如何求解进行详细介绍。数字卫星广播系统标准DVB-S中推荐的(133,171)卷积码是一种(2,1,d)卷积码,应用十分广泛,且有多种码率,所以本小节以(133,171)卷积码为例进行详细分析。该卷积码的生成多项式矩阵为G1/ 2(D)=[1+D2+D3+D5+D61+D+D2+D3+D6],其删除卷积码的删除模式如表1所示。

表1 (133,171)卷积码删除模式
下面将从解方程的角度出发直接求解得到校验向量,基本过程如下:首先根据式(15)建立多个方程构造出系数矩阵,然后利用高斯消元法化简系数矩阵,最后根据方程解的结构得到校验向量。



表2 QPSK相位模糊表
当调制方式改变时,不同相位模糊条件下符号与比特的映射关系仍然可以根据星座图的变化情况进行列表,这里不再赘述。
其次是构造数据矩阵。设校验向量h=(h1,h2,…,hl),l为h的长度;令c=(c1,c2,…,cL)代表编码数据,L为数据长度。将序列c带入式(15),可得下式
(ci,ci+1,…,ci+l-1)·hT=0
(16)
其中i是c中某个子码的起点,i=j·n+1(j=0,1,…),此处n的值根据码率及相位模糊具体情况取不同的值,具体取值情况见表3。由于0°与180°一致,90°与270°一致,所以表格中没有列出。倒谱存在与否不影响n的取值,因为倒谱不会影响码字比特的位置,而相位模糊可能会导致比特位置颠倒。原本n取值为奇数时,90°(270°)相位模糊导致比特颠倒后,相邻两行的码字位置不等价(即同一列相邻两行的比特在各个子码中的位置不一致),会造成方程只有0解,无法求解得到校验向量。为避免此问题,该种情况下将n值取为原值的2倍,这样便可保证相邻两行的各个比特在子码中的位置是相同的。

表3 不同情况下移位n的取值
将式(16)转换至矩阵形式,即
(17)
由式(17)可以看出,该问题是一个二元域方程组求解问题,未知数个数为l。为了保证结果的正确性,数据矩阵(系数矩阵)的行数最好大于l,不妨取为2l。
系数矩阵经过初等行变换,可化简成如下形式
(18)
其中,k是系数矩阵的秩,且k (19) 令hk+1,…,hk+r分别取r阶单位阵的每一行,可得到r个线性无关的解向量,将每个解向量作为矩阵的一行,可得到校验矩阵H如下 (20) 综上可知,将构造的数据矩阵初等行变换后,只需要再模2加上一个l阶单位阵,便可以得到所有校验向量,为了降低计算量,可以取其中长度最短的校验向量对卷积码进行校验识别。而本文研究的(133,171)卷积码及其删除码都只有一个校验向量,因此r=1,只需要将模2加单位阵后矩阵列不是0向量的第一列取出即可。 4.1小节介绍了各种条件下校验向量的求解方法,本小节将对校验向量如何应用于卷积码识别进行阐述。由于本文研究重点是卷积码闭集识别,因此下面重点介绍卷积码闭集识别中常用的校验关系验证法。校验关系验证法是指利用接收数据计算各个校验向量的平均符合度,平均符合度最高的校验向量对应的编码方式便是该接收数据的编码方式。目前已有的校验关系验证法有三种:Walsh-Hadamard变换(WHT)方法、对数似然比方法(LLR)和似然差方法(LD)。其中WHT方法利用硬判决序列,将式(15)中所有等式成立与不成立的概率之差作为校验向量对接收数据的符合度;而LLR和LD方法则是利用软判决序列,计算式(15)中每个等式成立的对数似然比和似然差,将平均对数似然比和平均似然差作为校验向量对接收数据的符合度。下面首先对一些数学符号进行定义,然后具体介绍三种方法的计算表达式。 第2节已经将符号序列映射到比特信息序列,为了保证本文数学符号的一致性,这里仍然采用第2节中定义的数学符号,具体定义如下:解调符号序列为r=(r1,r2,…,rL),L为符号序列长度;比特软信息序列为y=(y1,y2,…,y2L),符号ri对应的比特软信息为y2i-1和y2i,i=1,2,…,L;比特01序列为v=(ν1,ν2,…,ν2L),νj是yj的硬判决结果,j=1,2,…,2L;编码方式集合为Θ={C1,C2,…,CN},其中N是不同编码的个数(校验向量不同视为不同编码);校验向量为ht=(h1,h2,…,hut),ut(t=1,2,…,N)为编码方式t对应的校验向量长度;子码长度为n。 令S(ht)作为校验向量ht的平均符合度函数,Sj(ht)代表第j个校验方程的符合度,则有 (21) 其中,p为校验向量ht总的校验次数,计算方法如下 (22) 其中,[x]代表对实数x取整运算。 (1)WHT方法[14] WHT方法利用的是硬判决数据,将比特01序列v带入式(16),可得式(23) (23) 其中i是v中某个子码的起点,i=j·n+1(j=0,1,…)。根据WHT定义,符合度函数为 (24) (2)LLR方法[14] 设随机变量a∈GF(2),其LLR及在条件A下的LLR定义为 (25) (26) LLR方法利用的是软信息序列y,而式(16)中不涉及软信息,所以无法直接利用。实际上校验关系是指序列中某些特定位置的元素模2和为0,这里将关于ht的第j个校验关系记为T,ht中1元素位置记为l1,l2,…,lnt,0≤l1 (27) (28) 根据此定义以及一系列推导,得到校验关系T的LLR的具体表达式如下 (29) 具体推导过程见文献[14],这里不再赘述。 (3)LD方法[14] 设随机变量a∈GF(2),其LD及在条件A下的LD定义为 (30) (31) LD与LLR函数间的关系为 (32) 与上一小节类似,可知校验关系T的LD定义为 (33) 由式(29)、式(32)和式(33)可以推导得到,校验关系T的LD的具体表达式如下 (34) 设校验向量数目为N,每个校验向量长度和重量分别为ut和wt,t=1,2,…,N,每个校验向量对应的码字移位长度为nt,解调符号序列长度为L,则每个校验向量的校验次数可表示为 (35) 本节仿真实验以(133,171)卷积码为例展开测试。首先利用MATLAB产生足够长度的卷积码数据,然后利用该数据进一步产生两类数据:第一类数据是无噪声的各个条件下的01比特序列,此数据用来求解校验向量;第二类数据是含噪声的各个条件下的符号序列,此数据用来测试校验向量的识别性能。第一类数据产生不经过QPSK映射,倒谱对应I取反,相位模糊可以查表2;第二类数据产生需经过QPSK映射,叠加高斯白噪声,倒谱对应虚部变为相反数,相位模糊对应符号序列乘以ejθ(θ=0,π/ 2,π,3π/ 2);另外,按照实际通信过程,两种数据都必须在QPSK映射和倒谱、相位模糊之前通过表1产生各种码率数据。 表4给出了三种码率卷积码数据在倒谱、相位模糊条件下的校验向量,为便于分析以及对比,最后两行将校验序列分为两路列出。 表4 部分码率的校验向量 从前四行结果可以看出:(133,171)卷积码及其删除码对180°相位模糊透明,即仅通过校验向量无法判断是否存在180°相位模糊。这主要是因为0°相位模糊时校验向量1元素的个数为偶数且对应位置的数据也是偶数个1,即使数据存在180°相位模糊,校验向量1元素位置对应的数据仍是偶数个1,校验关系仍然成立,所以该校验向量不会发生变化。 对比第1、5、7行,可以发现码字存在倒谱时校验向量发生的变化:当把0°相位模糊的校验向量拆为两路时,如果单路中1元素个数为偶数,则倒谱条件下校验向量不会发生变化(3/4码率码字倒谱条件下校验向量未发生改变),否则校验向量会改变(1/ 2和2/3码率码字倒谱条件下校验向量均发生改变),且改变后校验向量是原校验向量移位对应码长后与原校验向量模2和的结果。这是因为倒谱对应第一比特I取反,当单路校验向量1元素个数为偶数时不影响模2和结果,为奇数时模2和结果必然改变,此种情况下设存在倒谱但不存在噪声的相邻两段校验序列为c1和c2,则有c1·hT=1和c2·hT=1,但同时c1·hT⊕c2·hT=0,因此,可知h′=h⊕(h移位n比特)。 对比最后两行结果,容易知码字在90°相位模糊加倒谱条件下,校验向量每两比特颠倒,这是因为此种情况下码字顺序变为QI。 通过表4可知,(133,171)卷积码在不同条件下的校验向量并不是完全不同,即校验向量数目并不是7·4·2=56种,由于该码字对180°相位模糊透明以及3/4、4/5、5/6三种码率卷积码在倒谱条件下校验向量不变,最终得到校验向量的数目为25种。实验利用这25个校验向量对数据计算对应的平均符合度,根据符合度最高的校验向量对应的码字条件便可以进一步判断数据的编码方式、倒谱和相位模糊的具体情况。 这里以两种码字条件为例说明如何根据检验向量判断码字的具体情况。第一种码字条件为1/ 2码率,无相位模糊,无倒谱,利用校验向量进行校验识别可以明确该码字码率为1/ 2,无倒谱,相位模糊可能是0°或者180°,只需要进一步分析0°和180°相位模糊两种情况即可;第二种码字条件为3/4码率,无倒谱,90°相位模糊,利用校验向量进行校验识别只能明确该码字码率为3/4,存在90°或者270°相位模糊,倒谱是否存在不确定,此种情况下需要进一步分析四种情况:90°相位模糊,无倒谱;90°相位模糊,有倒谱;270°相位模糊,无倒谱;270°相位模糊,有倒谱。对所有条件下码字进行校验识别并统计,发现校验识别后分析范围不是4种就是2种,即利用校验向量计算平均符合度的算法能够将分析范围从56种情况变为2种或者4种情况,大大降低了计算复杂度,提高了认知无线电系统的通信效率。 下面是仿真实验,给出了不同信噪比、不同数据量、不同码率等情况下三种方法的识别性能,实验中将码字对应的校验向量平均符合度取得最大值视为识别成功,各个仿真结果图的识别率指的是数据对应编码方式的识别正确率。实验中虽然只对两种码率的卷积码进行了测试,但对于其他码率卷积码的各个条件仍然适用,只是识别性能上有所改变。 设数据量(符号序列长度)L=200,码字条件为2/3码率、无倒谱和相位模糊,蒙特卡洛实验次数为3000次。图2给出了不同信噪比条件下,2/3码率卷积码识别正确率的变化曲线。由图2可以看出,利用解调软判决数据的LLR和LD方法性能相近,对卷积码的识别性能较利用硬判决数据的WHT方法要好很多,在识别率为90%时,LLR和LD方法较WHT方法约有2 dB的增益。LLR和LD方法性能相近是因为两者的具体表达式中仅仅相差了一个tanh逆函数,且该函数为单调函数,但LD由于少了tanh逆运算,计算量较LLR有所下降;LLR和LD方法对卷积码的识别性能优于WHT方法是因为LLR和LD方法充分利用了软判决数据中的可靠度信息,而WHT方法仅仅利用了数据中的符号信息。 图2 不同信噪比下2/3码率卷积码识别率 设信噪比Eb/N0=0 dB,码字条件为2/3码率、无倒谱和相位模糊,蒙特卡洛实验次数为3000次。图3给出了不同数据量条件下,码字识别率的变化曲线。由图3可以看出,三种方法在相同信噪比条件下的识别率随数据量的增加而提高;在数据量为700时,LLR和LD方法对卷积码的识别率已经接近100%,而WHT方法在数据量为1500时识别率仍没有达到100%且提高幅度越来越小,即相同识别率条件下,LLR和LD方法所需数据量较WHT方法要少得多,这些都是使用软信息所带来的优势。 图3 不同数据量下2/3码率卷积码识别率 设数据量L=200,码字条件为7/8码率、无倒谱和相位模糊,蒙特卡洛实验次数为3000次。图4给出了不同信噪比条件下,7/8码率卷积码识别正确率的变化曲线。由图4可以看出,信噪比低于3.5 dB时,WHT方法的性能优于LLR和LD方法,LLR方法的识别率在所有信噪比下均低于另外两种方法。这主要是因为7/8码率卷积码的校验向量长度为50,其中1元素个数为32,根据式(29)和式(34),LLR和LD方法需要将这32个位置对应的tanh值相乘,而tanh值在-1到1之间,其中若有一些较接近于0的数值便会导致LLR和LD方法求得的符合度较低,识别率随之而降低。对比图2和图4,可知LLR和LD方法在低码率码字识别性能上有较大优势,而WHT方法在识别高码率码字上稍有优势。 图4 不同信噪比下7/8码率卷积码识别率 图5给出了不同信噪比条件下,2/3码率卷积码存在倒谱时,码字识别正确率的变化曲线。此时数据量L=200,码字条件为2/3码率、存在倒谱、无相位模糊,蒙特卡洛实验次数为3000次。图2和图5对比可以看出,相同信噪比条件下,2/3码率卷积码存在倒谱时,三种方法的识别率均低于不存在倒谱时的情况,且在识别率达到90%时,LLR和LD方法较WHT方法仅有1 dB的增益,低于不存在倒谱时的2 dB增益。这主要是因为2/3码率卷积码存在倒谱时,对应的校验向量中1元素的数目增加,对于WHT方法会导致硬判决数据与校验向量正交概率降低,对于LLR和LD方法会导致tanh值相乘更容易取到较小值,因此三种方法识别率均有所下降。 图5 存在倒谱时2/3码率卷积码识别率 图6给出了不同信噪比条件下,2/3码率卷积码存在90°相位模糊时,码字识别正确率的变化曲线。此时数据量L=200,码字条件为2/3码率、无倒谱、存在90°相位模糊,蒙特卡洛实验次数为3000次。图5和图6对比可以看出,三种方法对这两种条件下的卷积码识别性能基本一致,这是因为两者的校验向量中1元素的数目相同,对tanh值相乘和校验向量与硬判决码字正交概率的影响基本一致。 图6 存在90°相位模糊时2/3码率卷积码识别率 图7给出了不同信噪比条件下,2/3码率卷积码存在倒谱和90°相位模糊时,码字识别正确率的变化曲线。此时数据量L=200,码字条件为2/3码率、有倒谱、存在90°相位模糊,蒙特卡洛实验次数为3000次。图2和图7对比可以看出,两种情况下识别曲线差异较小,这是因为对于QPSK映射,倒谱和90°相位模糊同时存在时码字的变化仅仅是两比特颠倒,对应的校验向量也是同样的变化,校验向量的长度以及1元素的数目没有改变。 图7 存在倒谱和90°模糊时2/3码率卷积码识别率 为说明本文算法的适用性,下面以(247,371)卷积码为例,映射方式为8PSK,重复以上实验过程。(247,371)卷积码是(2,1,7)卷积码,该卷积码同样有多种删除模式,其生成多项式矩阵为G1/ 2(D)=[1+D2+D5+D6+D71+D+D2+D3+D4+D7],其删除卷积码的删除模式如表5所示。 表5 (247,371)卷积码删除模式 8PSK映射条件下,符号信息到比特软信息的转化可以通过第2节中类似方法推导得到,这里不再赘述。由于8PSK各种条件下校验向量之间的关系比较复杂,这里不再列表说明,仅以两种码字条件为例说明如何根据检验向量判断码字的具体情况。第一种码字条件为1/ 2码率,无相位模糊,无倒谱,利用校验向量进行校验识别可以明确该码字码率为1/ 2,无倒谱,相位模糊为0°或者有倒谱,相位模糊为180°,只需要进一步分析无倒谱,相位模糊为0°和有倒谱,相位模糊为180°两种情况即可;第二种码字条件为2/3码率,45°相位模糊,无倒谱。利用校验向量进行校验识别能直接识别出该码字码率为2/3,存在45°相位模糊,无倒谱。对所有条件下码字进行校验识别并统计,发现校验识别后分析范围不是2种就是1种,即利用校验向量计算平均符合度的算法能够将8PSK分析范围从112种情况变为1种或者2种情况,这表明本文算法的适用性较强。 图8、图9、图10分别给出了不同信噪比条件下,2/3码率卷积码在无相位模糊、90°相位模糊和135°相位模糊时,码字识别正确率的变化曲线。此时数据量L=1000,蒙特卡洛实验次数为3000次。可以看出,映射方式为8PSK时,三种条件下三种方法仍然适用,且LLR和LD方法的效果仍然优于WHT,与前面结论一致。 图8 不同信噪比下2/3码率卷积码识别率 图9 存在90°相位模糊时2/3码率卷积码识别率 图10 存在135°相位模糊时2/3码率卷积码识别率 本文针对倒谱和相位模糊条件下不同码率卷积码识别问题,提出了一种容错能力较强的识别算法。以(133,171)卷积码为例,该算法首先推导得到QPSK调制方式下符号信息到比特软信息的转换关系,然后利用解方程求得各个条件下的校验向量,最后利用三种方法对所得校验向量的识别性能进行了测试,实现了不同码率、倒谱和相位模糊存在条件下的卷积码闭集识别。仿真结果表明,本文算法能够在较低信噪比下有效识别出码字码率、倒谱与相位模糊,且将分析范围从56种情况减少至2种或者4种分析情况,大大降低了计算复杂度,能够适用于实际环境需求。 [1] 解辉,黄知涛,王丰华. 信道编码盲识别技术研究进展[J]. 电子学报, 2013, 41(6): 1166-1176. Xie H, Huang Z T, Wang F H. Research progress of blind recognition of channel coding[J]. Acta Electronica Sinica, 2013, 41(6): 1166-1176.(in Chinese) [2] Lint J H. Introduction to Coding Theory[M]. Beijing: World Publishing Corporation, 2003. [3] 涂榫,高勇. 标准卷积码在QPSK相位模糊下的研究[J]. 通信技术, 2014, 47(9): 1004-1009. Tu S, Gao Y. Standard convolution code in condition of QPSK phase-ambiguity[J]. Communications Technology, 2014, 47(9): 1004-1009.(in Chinese) [4] Marazin M, Gautier R, Burel G. Blind recovery ofk/nrate convolutional encoders in a noisy environment[J]. EURASIP Journal on Wireless Communications and Networking, 2011, 2011:168. [5] Marazin M, Gautier R, Burel G. Some interesting dual code properties of convolutional encoder for standards self recognition[J]. IET Communications, 2012,6(8):931-935. [6] Wang F, Huang Z. A method for blind recognition of convolution code based on Euclidean algorithm[C]∥IEEE International Conference on Wireless Communications Networking and Mobile Computing, Shanghai: IEEE Press, 2007: 1414-1417. [7] 解辉,王丰华,黄知涛,等.基于改进欧几里得算法的卷积码快速盲识别算法[J].国防科技大学学报,2012, 34(6):158-162. Xie H, Wang F H, Huang Z T. A fast method for blind recognition of convolutional codes based on improved Euclidean algorithm[J]. Journal of National University of Defense Technology, 2012, 34(6):158-162.(in Chinese) [8] 刘建成, 杨晓静. 基于求解校验序列的(n,1,m)卷积码盲识别[J]. 电子与信息学报, 2012, 34(10): 2363-2368. Liu J C, Yang X J. Blind recognition of (n,1,m) convolutional code based on solving check-sequence[J]. Journal of Electronics & Information Technology, 2012, 34(10): 2363-2368.(in Chinese) [9] 刘健,王晓君,周希元.基于Walsh-Hadamard变换的卷积码盲识别[J].电子与信息学报,2010, 32(4): 884- 888. Liu J, Wang X J, Zhou X Y. Blind recognition of convolutional coding based on Walsh-Hadamard transform[J]. Journal of Electronics & Information Technology, 2010, 32(4): 884- 888.(in Chinese) [10] 解辉, 王丰华, 黄知涛. 基于最大似然检测的(n,1,m)卷积码盲识别方法[J]. 电子与信息学报, 2013, 35(7): 1671-1676. Xie H, Wang F H, Huang Z T. Blind recognition of (n,1,m) convolutional code based on maximum likelihood detection[J]. Journal of Electronics & Information Technology, 2013, 35(7): 1671-1676.(in Chinese) [11] 于沛东, 李静, 彭华. 一种利用软判决的信道编码识别新算法[J]. 电子学报, 2013, 41(2): 301-306. Yu P D, Li J, Peng H. A novel algorithm for channel coding recognition using soft-decision[J]. Acta Electronic Sinica, 2013, 41(2): 301-306.(in Chinese) [12] Yu P, Li J, Peng H. Gibbs Sampling Based Parameter Estimation for RSC Sub-codes of Turbo Codes[C]∥Sixth International Conference on Wireless Communications and Signal Processing, 2014:1-5. [13] Yu P, Li J, Peng H. A Least Square Method for Parameter Estimation of RSC Sub-Codes of Turbo Codes[J]. IEEE Communications Letters, 2014, 18(4):644- 647. [14] Yu P, Peng H, Li J. On Blind Recognition of Channel Codes within a Candidate Set[J]. IEEE Communications Letters, 2016, 20(4): 736-739.4.2 校验向量应用

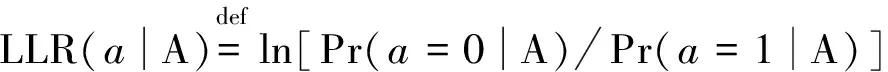
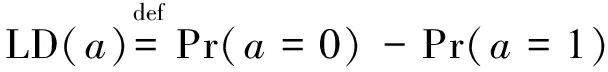

4.3 计算复杂度分析

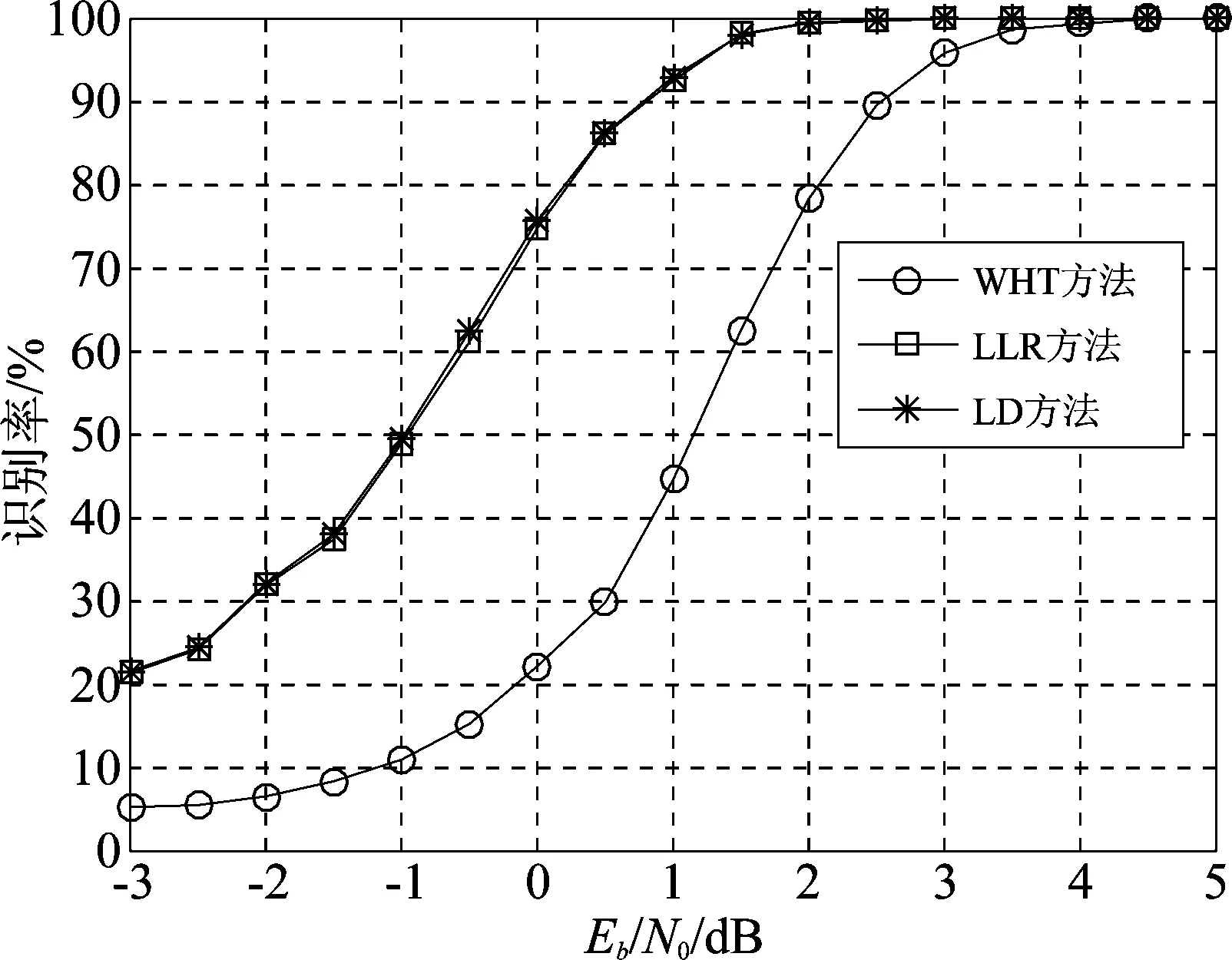
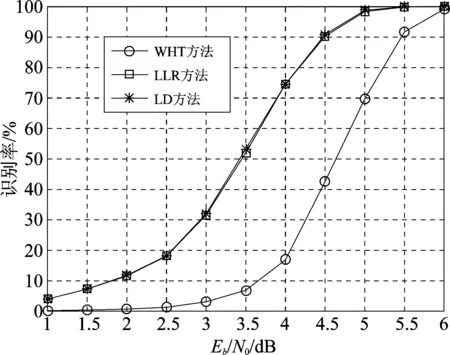
5 仿真实验及分析



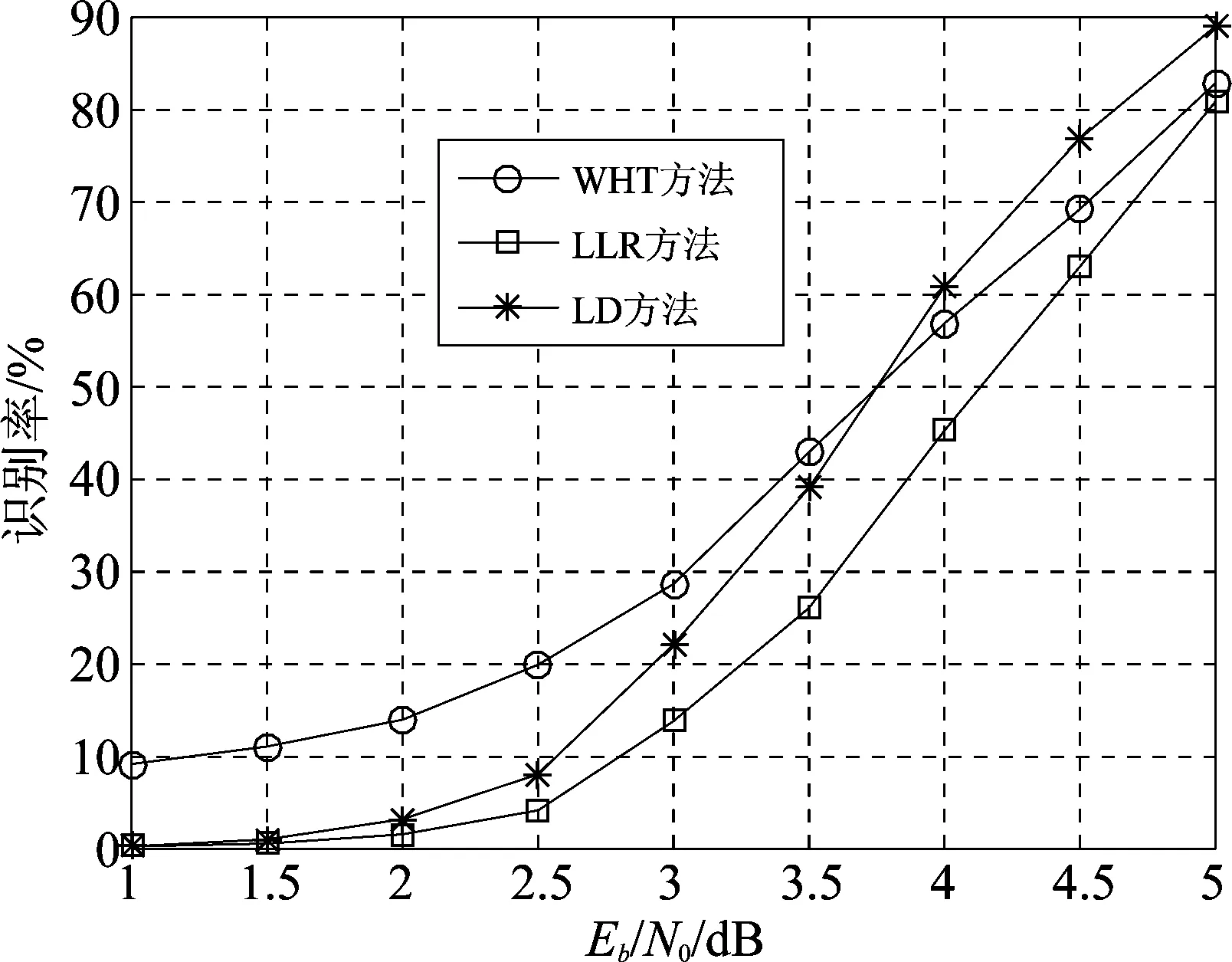



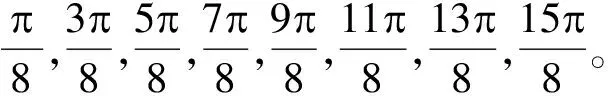


6 结论

