全双工大规模MIMO异构网络频谱效率分析及优化
沈哲贤 许 魁 王雨榕 王 萌
(解放军陆军工程大学通信工程学院,江苏南京 210007)
1 引言
伴随着移动用户数量的快速增长以及用户对高速数据通信的需求越来越大,下一代移动通信系统需要利用有限的频谱资源来不断提升吞吐量。为了满足这一需求,学者们对异构网络进行了深入研究。为了提供更大的覆盖范围和更高的数据吞吐量,需要在宏基站的覆盖范围内,根据用户分布情况和需求度,在合适的区域布置微基站。微基站与宏基站共享同一时频资源,但其发送功率更低,覆盖范围更小(通常40 m)[1],从而发送信号的路径损耗更少,信干噪比(signal-to-interference-plus-noise ratio,SINR)更大。因而可以有效地解决室内覆盖和热点问题[2- 4]。
然而,在实际系统中许多因素会对异构网络的性能造成影响。首先,异构网络的能量效率受限于无线回程链路。不合理的回程链路设计会使得异构网络的能量效率低于传统蜂窝网[5]。其次,文献[6]指出微小区的半径和分布也会对异构网的性能造成影响。影响异构网性能的最重要的因素是宏小区与微小区之间的跨层干扰。严重的跨层干扰降低了通信质量和数据速率。学术界针对影响因素展开了一系列研究。文献[5]提出具体的无线回程链路的设计方案。文献[7- 8]提出了一种空分干扰和协作波束成形方案来消除跨层干扰。文献[9]提出一种部分跨层干扰消除算法来提升网络性能。文献[10]提出基于几何规划的用户接入和功率控制联合优化方案,以降低基站总发射功率。
和半双工方式相比(time/frequency division duplex, TDD/FDD),全双工技术的应用使基站同时收发信号,理论上使系统传输效率加倍[11]。然而收发天线间引入的较强自干扰,给全双工技术的实际应用带来挑战。幸运的是,无线传播域、模拟域和数字域的自干扰抑制技术取得长足进步,使得自干扰抑制后,残余自干扰减少到相对较低的水平,从而真正实现全双工的性能增益。实验证明,全双工技术已能够满足WiFi系统的组网需求[12-14]。文献[15]将博弈论运用到全双工异构网中,从而优化系统和速率。
此外,大规模多输入多输出技术(multiple-input-multiple-output, MIMO)作为5G的关键技术之一,能够大幅提升单位时间内承载的并行数据流数,从而使系统频谱效率和能量效率倍增,可满足未来5G通信1000倍的容量需求[16-17]。和诸如脏纸编码的非线性处理方法相比,最大比合并(maximum ratio combining, MRC)和迫零(zero forcing, ZF)两种线性处理方法可逼近容量限(天线数趋向无穷)[18]。此外,基站与不同用户间的信道随天线数量增加而趋于正交,从而消除多用户干扰。
将全双工技术与大规模MIMO技术相结合,一方面在保持大规模MIMO性能增益的同时,利用全双工技术在时频维度引入的额外自由度达到降低系统设计复杂度的目的;另一方面,大规模MIMO空间高分辨率特性可降低自干扰抑制的难度。
在本文中,我们主要研究全双工大规模MIMO两层异构网络的系统性能。该网络由一个宏基站和多个微基站组成。每个宏基站和微基站都装配大规模均匀线性天线阵列(uniform linear antenna array, ULA)。本文的主要贡献如下:
(1)本文采用ZFR/ZFT 方法推导上下行渐近SINR的闭合表达式。
(2)本文提出基于几何规划(geometric programing, GP)的功率控制方案,优化了系统频谱效率。和传统的统一功率分配方案相比,基于几何规划的功率控制方案使异构网的频谱效率提升17.2%。
(3)本文提出基于部分用户选择(partial users selection, PUS)的跨层干扰消除方案。该方案利用ULA的高自由度来消除部分的跨层干扰,在功率控制方案的基础上使系统频谱效率提升14.6%。
(4)通过结合PUS方案和基于几何规划的功率控制方案,并进行迭代计算,异构网络的频谱效率与传统方案相比提升了59.1%。
2 系统模型
如图1所示,在一个全双工两层异构网络中,宏基站和K个微基站都装配大规模ULA。宏基站使用NM根天线发送信号,使用另外NM根天线接收来自宏小区用户的信号,宏小区上下行用户数各为M;每个微基站使用NP根发送天线和NP根接收天线,微小区上下行用户数均为L。我们假设所有用户设备工作在半双工模式,并且只装配单天线。我们主要关注由全双工和大规模MIMO技术带来的性能增益,而不是无线回程链路的具体设计细节,所以我们假设宏基站和微基站之间使用有线回程。
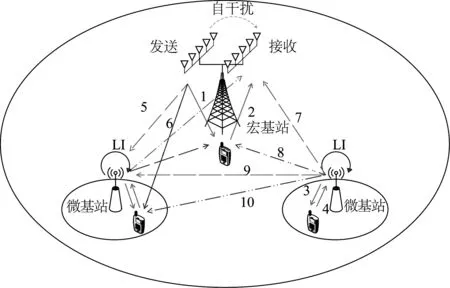
图1 全双工大规模MIMO两层异构网络
图1中的序号代表不同的信道,具体信道细节如表1所示。
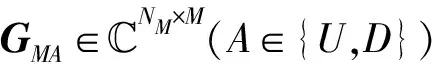

表1 图1中信道细节

2.1 信道估计
为了实现全双工传输,在信道相干时间内,基站需要利用部分时频资源来获取信道状态信息,即GMA和GPiA,(A∈{U,D})。假设基站的每个发送天线与额外的接收射频链路相连,上下行信道具有互易性。所有上下行用户同时向基站发送导频序列,为保证导频序列两两正交,导频长度τ≥用户数。 参考文献[19],信道矩阵的最小均方误差(minimum mean-square-error, MMSE)估计可以表达为
(1)

(2)

(3)
2.2 数据传输
2.2.1上行链路
宏基站接收信号表示为
(4)

设ai为矩阵A的第i列子矩阵,则宏基站接收的来自第m个宏小区用户的信号可表达为
(5)
式(5)右边第一项为有用信号,第二项为来自其他宏小区用户的多用户干扰。第三项代表宏基站收发天线间的自干扰。第四项代表微基站对宏基站的跨层干扰。类似的,第k个微基站的接收信号为
(6)
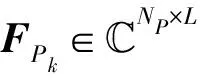
(7)
2.2.2下行链路
宏基站发送给用户的下行信号为
(8)
第m个用户接收到的信号表达式为
(9)
第k个微基站发送给其用户的下行信号表达式为
(10)
第l个用户接收到的信号表达式为
(11)
3 上下行信号渐近SINR分析
3.1 ZFR/ZFT
基站的接收检测矩阵和发送预编码矩阵可以表示为
(12)
3.1.1上行链路渐近SINR分析
将(1)、(12)代入(5),第m个用户发送给宏基站的信号可以表示为
(13)

(14)
当宏基站天线数量趋向于无穷时,宏小区上行渐近SINR如(15)所示。证明见附录。
(15)
采用相同的方法,第k个微小区上行渐近SINR如(16)所示。
(16)
3.1.2下行链路渐近SINR分析
参照上行渐近SINR推导方法,我们直接给出下行渐近SINR表达式,如(17)和(18)所示。
(17)
(18)
3.2 性能评估
3.2.1上下行信号遍历速率
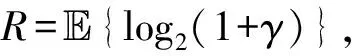
(19)
将(15)代入(19)可得上行信号遍历速率的下界为
(20)

(21)
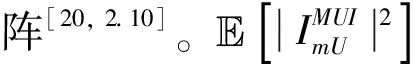
(22)
(23)
(24)
(25)
由式(22)~(25)可得,宏小区或微小区的上下行遍历速率的下界随天线数量的增加而增长。此外,采用功率控制方案和增加天线数量可抑制自干扰,跨层干扰和同层干扰。我们以式(22)为例进行分析。记
其中EmU,EmD,EPiD为正常数,0≤p,q,r≤1。则式(22)可变形为
(26)
由式(26)可得,当天线数量趋于无穷,信道估计误差将被消除;自干扰,跨层干扰和高斯白噪声的干扰强度受p,q,r控制。当p=1,q=r=0,即仅对宏小区上行链路进行功率控制,增加基站天线数量并不能抑制自干扰,跨层干扰和噪声;当0 3.2.2频谱效率 异构网络的频谱效率如式(27)所示 (27) 其中T是相干时间长度(以符号计量)。在相干间隔内,τ个符号用于训练,剩余资源用于数据传输。注意在ZF条件下,我们使用速率下界来计算频谱效率,且当天线数量很大时,可以认为该值为精确值。 在3.2.1节,我们已经证明采用功率控制和增加天线数量的措施可以提升异构网的频谱效率。在这一部分,我们提出一种基于几何规划的功率控制方案。在功率控制方案的基础上,我们也提出一种基于部分用户选择(PUS)的跨层干扰消除方案来消除部分跨层干扰并进一步提高频谱效率。 由于每个上/下行信号发送功率的选择导致不同程度的自干扰和跨层干扰,我们使用功率控制方案来合理分配发送功率,优化整个网络的频谱效率。 值得注意的是,基站在进行功率控制时,只考虑优化整体网络性能,这可能会引入不公平现象,导致个别用户通信质量较差。因此为了确保所有用户最基本的通信质量,上下行发送功率不得低于某一门限值。频谱效率优化问题可写成 (28) 为了简化计算,(28)可被化简为(29) (29) 其中各项系数如下所示: (30) (30)是一个标准的几何规划问题,我们使用算法1去解决。 算法1 使用GP解决问题(30)1.初始化: 利用(22^25)计算初始值^γ(1)mU,^γ(1)mD,^γ(1)i,jU,^γ(1)i,jD。 n=1,ε 表示容限制,L表示最大迭代次数。2.第n次迭代: (1)使用^γ(n)mU,^γ(n)mD,^γ(n)i,jU,^γ(n)i,jD计算葜mU,葜mD葜i,jU,葜i,jDηmU,ηmD,ηi,jU,ηi,jD(2)解决GP问题:min ∏m=M,i=K,j=Lm=i=j=1葜-1mU葜-1mD葜-1i,jU葜-1i,jDγ-ηmUmUγ-ηmDmDγ-ηi,jUi,jUγ-ηi,jDi,jDs.t. c1^c4,p1^p83.若maxm=1,…,M^γ(n)mU-^γ(n-1)mU<εmaxm=1,…,M^γ(n)mD-^γ(n-1)mD<εmaxi=1,…,Kj=1,…,L^γ(n)i,jU-^γ(n-1)i,jU<εmaxi=1,…,Kj=1,…,L^γ(n)i,jD-^γ(n-1)i,jD<εìîíïïïïïïïï或者n=L,停止计算。否则n=n+1, 回到第2步。 在一个蜂窝小区内,ZF方法可将其他用户信号投影到零空间,从而消除多用户干扰。基于此特点,我们提出一种基于PUS的跨层干扰消除方案来进一步提升异构网的频谱效率。这里PUS指宏基站或者微基站仅仅选择部分的用户来消除跨层干扰。 (31) (32) 将(31)、(32)与式(24)、(25)比较可发现,宏基站以损失天线自由度,降低下行速率为代价消除被选择用户的跨层干扰,提升微小区下行速率。异构网性能将受到影响。为最大化网络频谱效率,宏基站需以一定准则选择微小区用户消除跨层干扰,而不至于损失过多自由度。稍后我们介绍具体的用户选择准则。 同样PUS方案也可用于微基站。宏小区用户的SINR可写为 (33) 此处存在两种微小区用户的SINR。未被选择的微小区用户SINR可写为(34),被选择用户的SINR可写为(35)。 (34) (35) 算法2 PUS方案用户选择准则1.初始化:(1)SP=SM=1;利用(22)^(25)计算初始频谱效率SE′。 ε 表示容限值。(2)度量矩阵U∈^K×L,V∈^1×M,U=RP1-RP0,V=RM2-RM1。(3)设A=RP0,B=RM1。2.微小区的优化:当(SP 3.宏小区的优化:当(SM 通过仿真发现,执行该算法选择的用户均受到严重的跨层干扰。当宏基站用相同自由度消除此类用户的跨层干扰时,系统能够获得更多性能增益。在第5节,我们将证明功率控制方案和PUS方案都能够有效地提升网络频谱效率。事实上,通过结合这两种方法并加以迭代,频谱效率的提升更加显著。具体的迭代算法如算法3所示。 算法3 结合功率控制和PUS方案的迭代算法1.初始化: 用(22)^(25)计算统一功率分配方案下异构网络的初始频谱效率:SE′。SE=0,n=0,设L为最大的迭代次数。2.while(SE′>SE)&&(n 在这一部分,我们将验证理论分析结果。我们使用蒙特卡罗方法对MRC和ZF两种线性预编码/检测方法的性能进行对比。并且将功率控制和PUS方案与文献[8]采用的协作波束成形方案进行对比,验证所提方案的性能优越性。 为了避免微小区半径和分布对网络性能带来的额外影响,我们假设宏基站和微基站的半径分别是rm=500 m,rp=40 m,所有的微小区都处在宏小区的边缘。我们使用实际的大尺度衰落模型。该模型包括路径损耗,阴影衰落和收发端的随机位置[22]。大尺度衰落系数为 (36) 其中z为标准差为σdB的对数随机变量。ν为路径损耗指数,d为用户和基站间的距离,d0为参考距离。在城市场景中,我们假设σ=8 dB,ν=3.8,d0在宏小区和微小区内分别设为200 m和50 m。假设所有用户都均匀分布在小区内。参照文献[8]中的标准,仿真参数如下: 宏基站半径:rm=500 m;微基站半径:rp=40 m; 宏小区用户数:M=10; 微小区数量:K=2;微小区用户数:L=2; 采用MRC/MRT和ZFR/ZFT两种方法条件下,异构网频谱效率如图2所示。在半双工或者全双工模式下,ZFR/ZFT方法的性能高于MRC/MRT。因为对于干扰受限的异构网络,严重的跨层干扰和多用户干扰成为扰乱接收信号,降低网络速率的主要因素。使用MRC方法增加信号发送功率不能有效改善用户服务质量,而且还会对小区造成更严重的干扰。在ZF方法下,基站通过将干扰信号投影到零空间,可以消除多用户干扰,从而获取更好的性能增益。然而当天线数趋向无穷时,两种方法的性能曲线将趋于重叠。 图2 FD/HD模式下异构网频谱效率随天线数NM 的变化图, βLIM=βLIPk=0 dB 图3比较了4种不同方案的性能。在下行链路,采用功率控制方案使频谱效率提升4.5%,然而采用协作波束成形方案[8]性能仅提升1.2%。该方案性能增益有限的原因是宏基站不使用对微小区造成严重干扰的波束。在用户数较少的情况下天线自由度损失较大;此外,仅采用功率控制方案的性能低于IMP消除算法[9],因为仿真参数设置用户数较小,功率控制方案性能优势无法体现。而功率控制方案结合PUS方案性能优于[9],验证了算法3的性能优势。尽管(interference from Macro base station to Pico base station, IMP)消除算法能够有效提升频谱效率,但当天线数量很大时,该算法的优势将消失。 图3 异构网下行链路频谱效率随天线数NM (均匀线性天线阵列)的变化图 事实上当NM或NP增加到128时,IMP消除算法不能带来任何性能提升。因为选择任何微小区用户来消除IMP都将导致下行频谱效率下降。因此文献[9]提出的IMP消除算法受场景限制。该算法不适用于大规模天线阵列场景。 当小区内有更多用户时,仿真结果如图4所示。图4为上下行频谱效率随NM变化图。不同于图3,在用户数较多条件下,采用功率控制方案使频谱效率提升17.2%,其性能与IMP消除算法[9]近似相等。考虑上下行功率控制方案比仅仅考虑下行信号的功率控制方案更为有效,因为上下行链路相互影响,合理的功率分配方案能抑制跨层干扰和自干扰。迭代算法性能曲线表明,在经过功率控制和采用PUS方案后,仍有提升频谱效率的空间。经过2次迭代后,异构网络的频谱效率较不经过迭代提升16.4%,较统一功率方案相比,性能提升60.39%。 图4 异构网上行+下行频谱效率随天线数NM 的变化图,M=30,K=3,L=15,βLIM=βLIPk=0 dB,NP=100 本文研究全双工大规模MIMO两层异构网络。采用ZFR/ZFT方法推导了宏小区,微小区的上下行渐近SINR闭合表达式。理论分析表明,通过控制发送信号功率并增加天线数量,跨层干扰,自干扰和加性高斯白噪声能被有效压制。根据理论分析,本文提出一种基于几何规划的功率控制方案和PUS方案来提升网络频谱效率。在仿真部分,通过对比不同算法性能,验证了功率控制方案和PUS方案的优越性和灵活性。 (37) 其中‖fM,m‖2可重写为 (38) (39) (40) (41) (42) (43) 将(43)代入(42)可得: (44) (45) (46) [1] 3GPP. TR36.814.—2010, Further advancements for E-UTRA Physical layer aspects[S]. France: 3GPP, 2010. [2] Huang Y, He S, Jin S, et al. Area-classified interference coordination for heterogeneous cellular network[J]. EURASIP J. Wireless Comm. and Networking, 2014, 2014(1):1-16. [3] Ye Q, Rong B, Chen Y, et al. User association for load balancing in heterogeneous cellular networks[J]. IEEE Trans. Wireless Commun., 2013, 12(6):2706-2716. [4] Dhillon H S, Kountouris M, Andrews J G. Downlink MIMO hetnets: Modeling, ordering results and performance analysis[J]. IEEE Trans. Wireless Commun., 2013, 12(10): 5208-5222. [5] Yang H H, Geraci G, Quek T Q S. Energy-Efficient Design of MIMO Heterogeneous Networks With Wireless Backhaul[J]. IEEE Transactions on Wireless Communications, 2016, 15(7): 4914- 4927. [6] Fehske A J, Richter F, Fettweis G P. Energy Efficiency Improvements through Micro Sites in Cellular Mobile Radio Networks[C]∥IEEE Globecom Workshops. Honolulu HI, 2009: 1-5. [7] Huang Y, Zheng G, Bengtsson M, et al. Distributed multicell beamforming design with limited intercell coordination[J]. IEEE Trans. Signal Process., 2011, 59(2): 728-738. [8] Zhang F, Huang Y, Jin S, et al. Reduced-backhaul coordinated beamforming for massive MIMO heterogeneous networks[C]∥ IEEE Wireless Communications and Networking Conference (WCNC).New Orleans LA, 2015: 129-134. [9] Liu Y, Lu L, Li G, et al. Performance analysis and interference cancellation for heterogeneous network with massive MIMO[C]∥ IEEE Global Conference on Signal and Information Processing (GlobalSIP).Orlando FL, 2015: 888- 892. [10] 赵景, 韩圣千. 协作异构网络中的用户接入与功率控制联合优化[J]. 信号处理, 2015, 31(10): 1279-1286. Zhao Jing, Han Shengqian. Joint Optimization of User Access and Power Control in Cooperative Heterogeneous Networks[J]. Journal of Signal Processing, 2015, 31(10): 1279-1286.(in Chinese) [11] Shojaeifard A, Wong K K, Renzo M D, et al. Full-duplex versus half-duplex large scale antenna system[C]∥ 2017 IEEE International Conference on Communications Workshops. Paris France, 2017: 743-748. [12] Riihonen T, Balakrishnan A, Haneda K, et al. Optimal eigenbeamforming for suppressing self-interference in full-duplex MIMO relays[C]∥ 45th Annual Conference on Information Sciences and Systems. Baltimore, MD, 2011:1- 6. [13] Riihonen T, Werner S, Wichman R. Mitigation of loopback self-interference in full-duplex MIMO relays[J]. IEEE Transactions on Signal Processing, 2011, 59(12): 5983-5993. [14] Sabharwal A, Schniter P, Guo D, et al. In-Band Full-Duplex Wireless: Challenges and Opportunities[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(9): 1637-1652. [15] Yuan S, Liang Q. Game Theoretical Method for Sum-Rate Maximization in Full-Duplex Massive MIMO Heterogeneous Networks[C]∥IEEE 12th International Conference on Mobile Ad Hoc and Sensor Systems. Dallas TX, 2015: 610- 615. [16] Rusek F, Persson D, Lau BK, et al. Scaling Up MIMO: Opportunities and Challenges with Very Large Arrays[J]. IEEE Signal Processing Magazine, 2013, 30(1): 40- 60. [17] Wang X, Zhang D, Xu K, et al. On the energy spectral efficiency of multi-user full-duplex massive MIMO systems with power control[J]. Eurasip Journal on Wireless Communications & Networking, Shenzhen, 2017(1): 82. [18] Ngo H Q, Larsson E G, Marzetta T L. Energy and Spectral Efficiency of Very Large Multiuser MIMO Systems[J]. IEEE Trans. Commun., 2013, 61(4): 1436-1449. [19] Ngo H Q, Suraweera H A, Matthaiou M, et al. Multipair Full-Duplex Relaying With Massive Arrays and Linear Processing[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(9): 1721-1737. [20] Tulino A M. Random matrix theory and wireless communications[M]. Now Publishers Inc, 2004. [21] Weeraddana P C, Codreanu M, Latva-aho M, et al. Resource allocation for cross-layer utility maximization in wireless networks[J]. IEEE Trans.Veh.Technol., 2011, 60(6): 2790-2809. [22] Choi W, Andrews J G. The capacity gain from intercell scheduling in multi-antenna systems[J]. IEEE Trans. Wireless Commun., 2008, 7(2): 714-725. [23] Cramér H. Random variables and probability distributions[M]. 3rd ed. Cambridge University Press, 1970. [24] Evans J, Tse D N C. Large system performance of linear multiuser receivers in multipath fading channels[J]. IEEE Trans. Inf. Theory, 2000, 46(6): 2059-2078.4 频谱效率的优化
4.1 功率控制



4.2 基于部分用户选择的跨层干扰消除方案



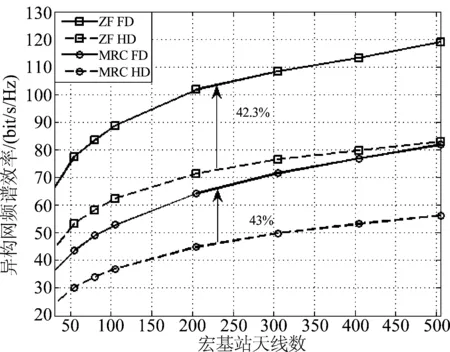
5 仿真结果



6 结论
附录 采用ZF方法计算渐近 的证明






