复杂环境下基于CFSFDP的自适应室内定位方法
刘 影 贾 迪 王和章
(辽宁工程技术大学电子与信息工程学院,辽宁葫芦岛 125105)
1 引言
随着移动互联网和智能终端的蓬勃发展,位置信息服务已受到研究人员广泛关注。尽管传统的GPS(global positioning system)定位和蜂窝定位技术在室外开阔环境中能达到较高的定位精度,但在室内和恶劣环境下无法进行有效定位,随着Wi-Fi网络的普及和高速发展,利用无线Wi-Fi实现室内定位已成为研究热点[1-3]。其中,基于位置指纹的Wi-Fi定位被广泛研究。
位置指纹算法[4-5]是一种两个阶段的定位算法,可分为训练阶段(离线)和定位阶段(在线)。离线阶段主要为数据采集阶段,在定位区域内选择一些位置点作为采样点,从附近的AP获取RSSI (received signal strength indication)形成指纹,并创建位置指纹库,其中每个指纹都对应于唯一位置。在线阶段为实时定位阶段,需要待测目标测量的指纹与指纹库中的指纹进行匹配,从而估计出待测目标对应的位置信息。在以往的众多研究中,提出了许多基于统计学习的方法,如聚类、贝叶斯、核函数等位置预测方法,用来提高位置指纹的准确性及接入点(Access Point,AP)的选择。例如,Wei Zhang[6]等人针对AP的选择问题,给出了一种基于WKNN和朴素贝叶斯域聚类室内位置估计策略,有效的解决了AP的可靠性问题。李华亮[7]等人提出一种基于核的数据处理方法训练位置指纹数据,将位置指纹映射到高维空间进行分析,挖掘出更多位置指纹特性。田洪亮[8]等人采用K-Means聚类算法对位置指纹进行聚类,以减少在线阶段指纹的匹配次数。
然而由于室内布局的复杂性,Wi-Fi信号在传输过程中,容易受到障碍物等因素的影响,导致散射、反射、衍射现象和多径效应的发生,使终端所收集到的信号强度具有较大的随机性和不稳定性[9-11]。因此,每个采样点上所采集到AP的RSS信号往往表现出不稳定,而基于确定性的指纹算法,如K近邻(KNN,k-nearest neighbor)算法以及加权k近邻(WKNN,weight k-nearest neighbor)算法都是通过接收来自附近AP的RSS信号建立指纹数据库,所以这两种算法中实时的定位点不能自适应的获取稳定且有效AP的RSS值。王磊[12]等人提出一种自适应获取WKNN有效接入点,解决了WKNN匹配准确度不高的问题。
不同的基于指纹的室内定位算法,多数是针对离线阶段指纹库的滤波处理以及对在线阶段的匹配算法进行优化,而很少讨论目标在定位区域内的行为特征。例如计算出目标与AP之间的直线距离,可缩小对比指纹数据库的范围,减少比较次数。因此,建立良好的室内距离估计数学模型是实现高精度定位的重中之重。当模拟无线电传播时,人们总是简化假定遮蔽衰落是一个静态值。事实上,遮蔽衰落是用来反映环境复杂性的,在实验过程中会对物理环境中微小的变化很敏感。因此,传统的理论信号衰减模型难以满足真实复杂的室内传播环境[13]。为确保算法设计的准确性和高效率,性能分析、系统优化和良好的数学模型必不可少[14]。
综合以上分析,本文主要研究在复杂环境下的指纹定位方法。利用CFSFDP[15](Clustering by Fast Search and Find of Density Peaks)聚类方法训练原始位置指纹,即有效的处理指纹中“离群点”,且可以把采集到的指纹数据进行分簇,分析其指纹的内在相似性和外在差异性,进而寻找出最优指纹数据点,在此基础上构建正六边形指纹地图;在线阶段提出一种自适应距离传播模型,用于指导待定位目标搜索指纹库区域,从而减少指纹搜索范围。本文算法实验均来自于真实的环境,实验数据表明本文算法的定位误差和时间复杂度优于KNN和WKNN,并且在室内复杂环境下具有良好的性能。
2 复杂环境下的自适应室内定位方法——ALCCE
本文提出一种复杂环境下基于CFSFDP的自适应室内定位方法,命名为ALCCE(Adaptive indoor localization algorithm of based on CFSFDP in complex environment)定位算法,具体方案如图1所示。离线阶段和在线阶段所采集到的RSS数据需要进行预处理,主要是对原始数据进行去噪。在离线阶段根据处理后的数据建立指纹地图,并建立指纹数据库。在线阶段,采用自适应信号传播模型计算出待定位目标与AP的距离d,将待定位目标采集的指纹与指纹库中与AP距离为d的指纹进行匹配,最后将距离匹配度最高的指纹对应的位置作为移动目标的位置。

图1 ALCCE方案
2.1 原始指纹经CFSFDP的处理方法
通过大量的测试发现,无线Wi-Fi信号很容易受到环境的影响,使得RSS存在时变特性,从而在同一通信节点一段时间内获取的RSS信号存在较大差异性,很难准确估计出到达AP之间的距离。因此,单个数据包产生RSS数据无法准确反映出有效信息,如图2所示。图中横坐标表示采样点与AP的距离,单位为m;纵坐标表示单个数据包的方差,每个采样点连续采集RSS数据3分钟作为一个RSS数据包。为了解决信号时变对定位误差的影响,本文在建立指纹库之前先采用CFSFDP聚类算法对RSS数据进行统计分布分析,以确保数据的稳定性和有效性,作为后续指纹库的构建和进行指纹匹配的基。

图2 单个数据包的方差图
CFSFDP[15]是一种综合考虑局部密度和距离的聚类算法,其核心思想在于对聚类中心的刻画。聚类中心应具有两个特点:与周围节点相比自身密度最大;与其他聚类中心之间有足够大的距离。利用这两个特点将在同一个通信节点处的RSS数据点进行归类,进而识别出离群点。

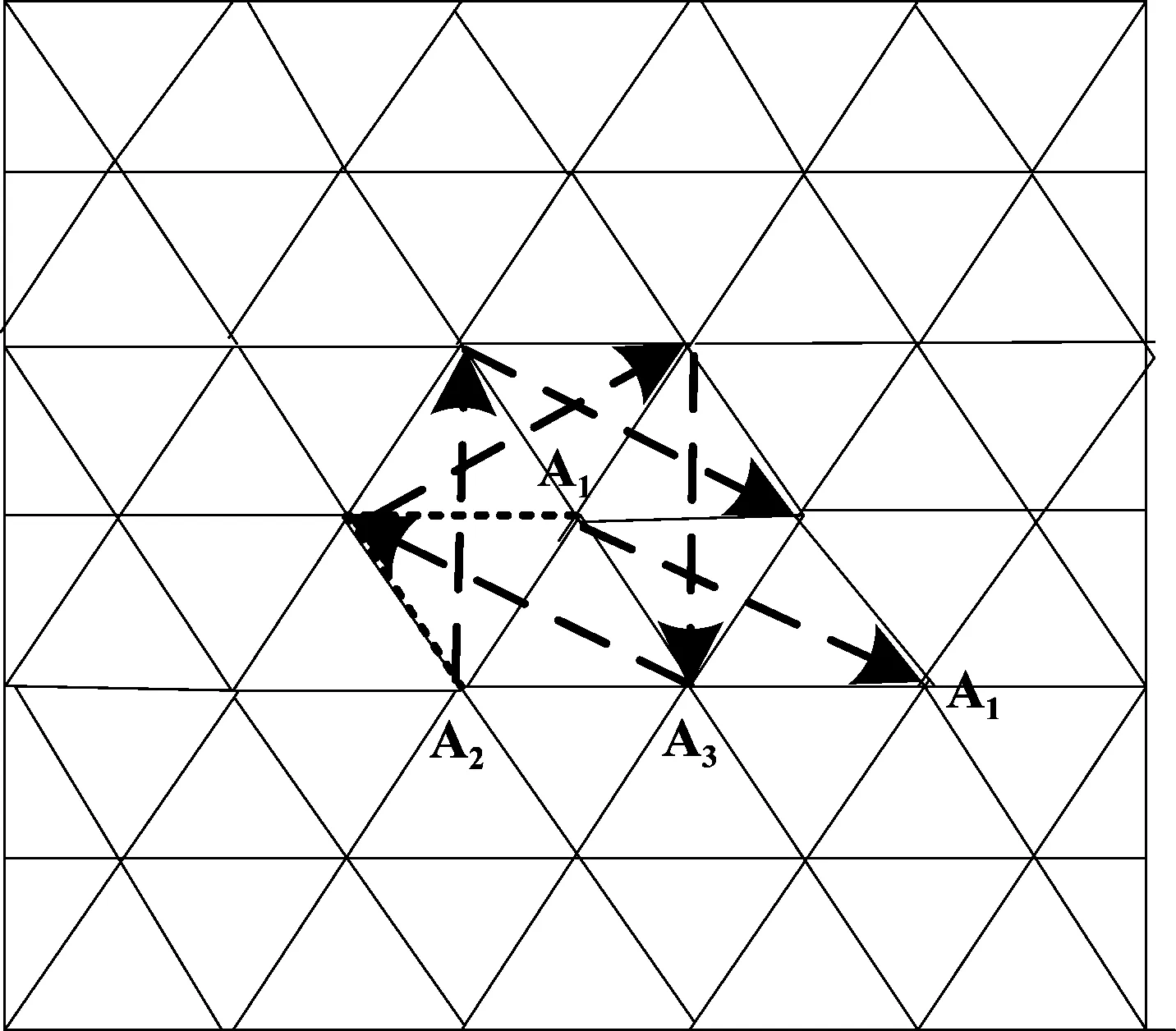
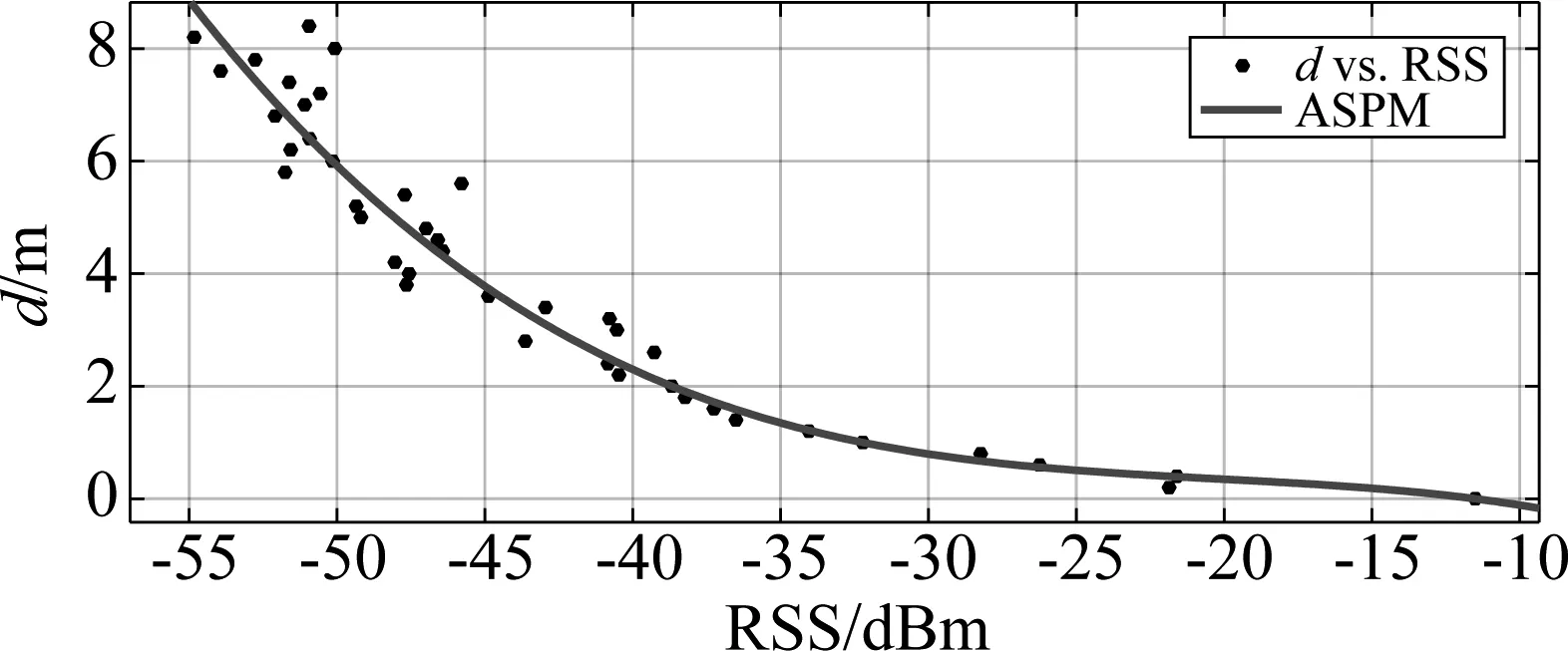
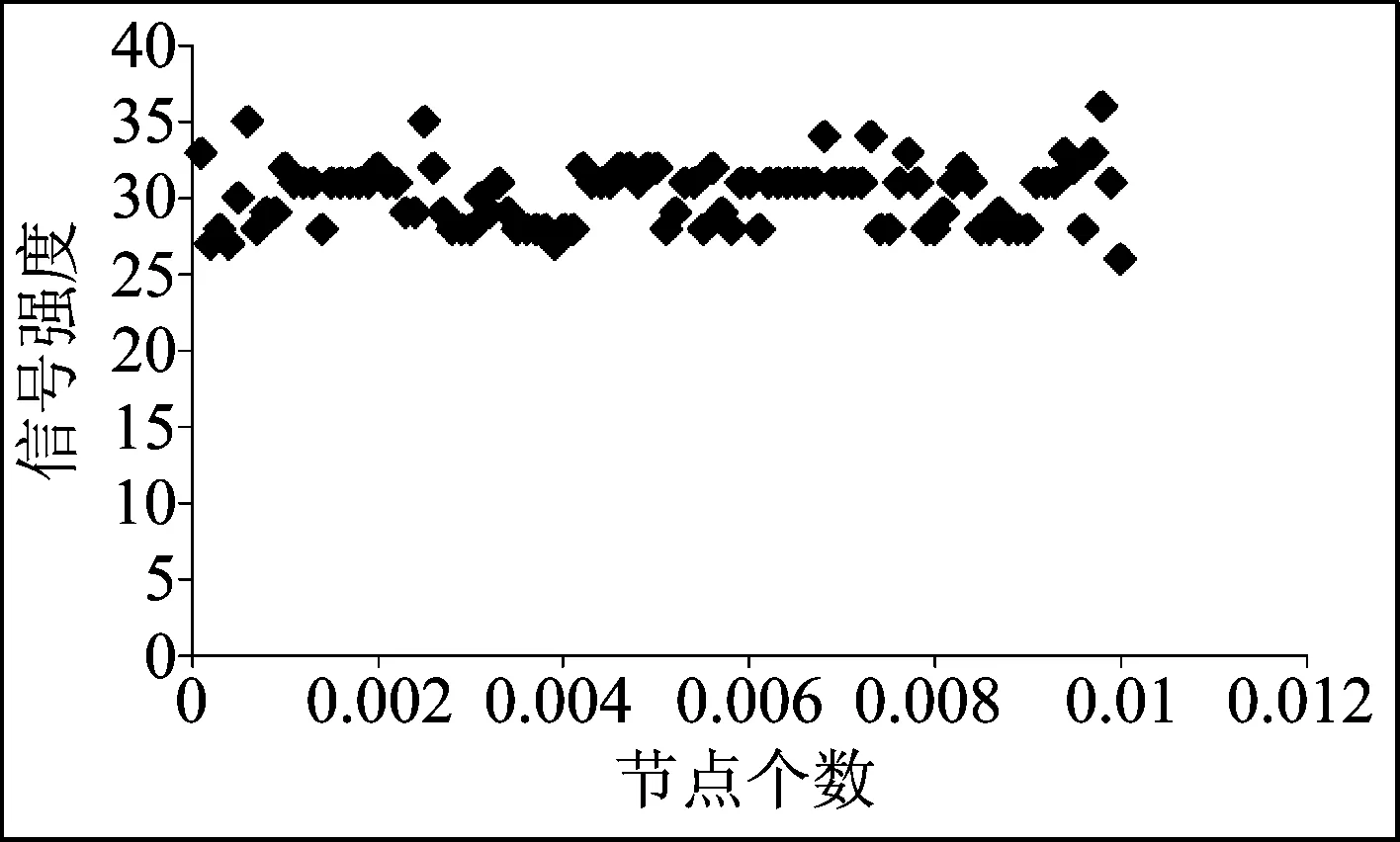
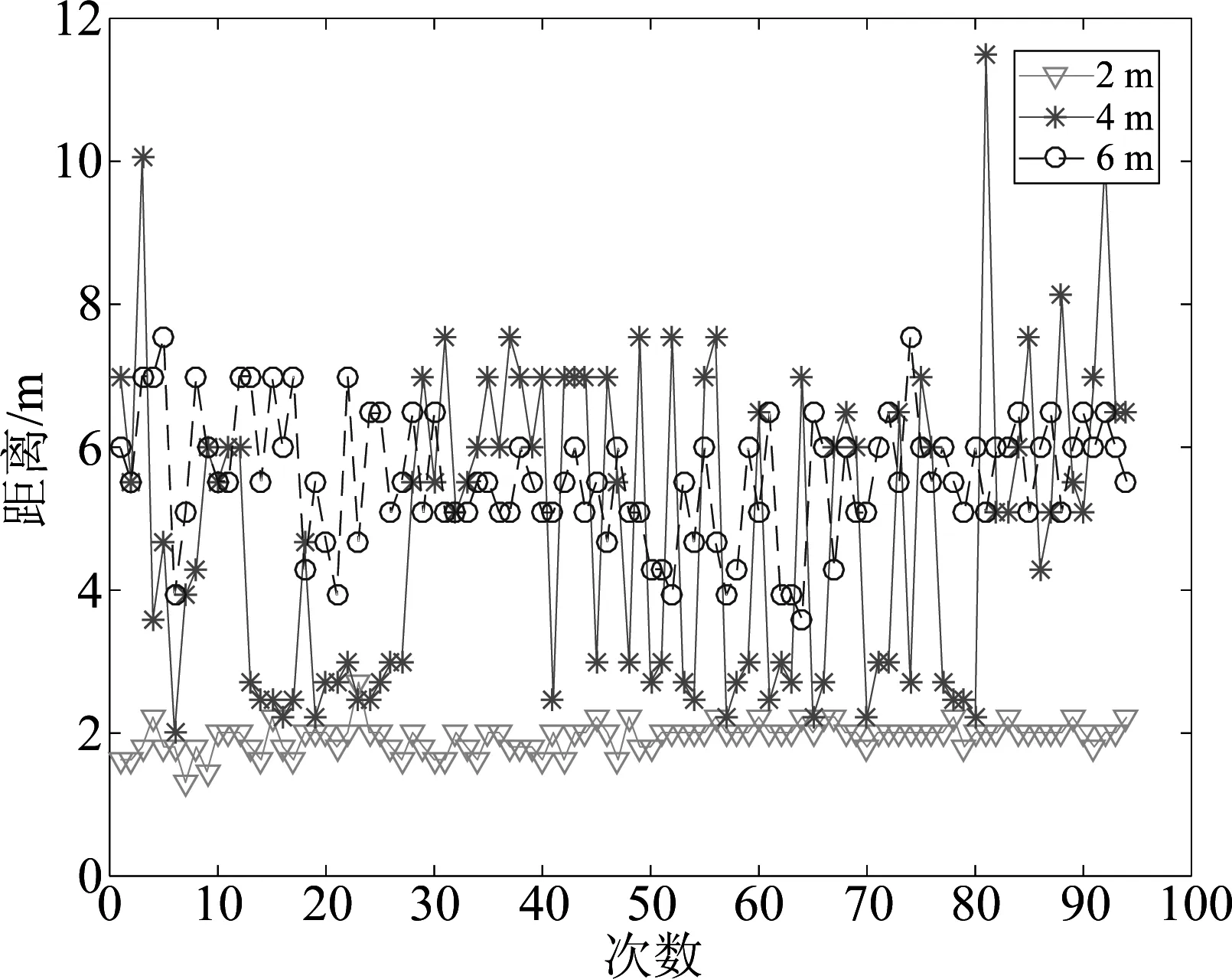
步骤1为了使数据集适合于该聚类算法首先将RSSi映射到二维空间,计算出任意两个数据点的距离dij=dist(RSSi,RRSj),表示数据点RSSi和RSSj之间的距离,令dij=dji,i d1≤d2≤…≤dK (1) 取dc=df(Kt),f(Kt)表示对Kt进行四舍五入运算,t取经验值0.02,详见参考文献[15]。dc决定聚类算法的成败,如果dc过大,使得每个数据点的局部密度值都很大以至于区分度不高,当dc大于距离dij最大值时,则所有数据点都归为一个簇,当dc小于距离dij最小值时,每个数据点都单独成为一个簇,导致无法对数据集S分类。 步骤3根据dij和dc计算出局部密度ρi,ρi主要用来刻画聚类中心的邻居节点个数。邻居节点个数越多,其局部密度越大;反之,其局部密度越小。根据局部密度的含义,其表达式为: (2) 其中,dc为截断距离。对于(2)可知,与数据点RSSi的距离小于dc的节点数越多,ρi越大。 ρq1≥ρq2≥…≥ρqN (3) (4) δqi越大,说明数据点RSSi作为聚类中心时与其他聚类中心的距离越大。根据局部密度ρ和距离δ的含义可以得出,当某一数据点的ρ值越大,且δ值越大,其该点成为聚类中心的可能性越大。 (5) (6) cqi=cnqi (7) 定位区域内每个节点通过连续收集多个数据包,根据步骤1~步骤4计算出所有数据点的局部密度ρ和距离δ,画出关于ρ和δ决策图,根据聚类个数选出聚类中心点,再根据步骤5对数据进行分类,确定非聚类中心点归属于哪一个簇,进而可分析出离群点。 图3 聚类流程图 基于指纹的Wi-Fi室内定位方法通常将定位区域划分为网格状,将当前收集的指纹数据与指纹库中所有项进行比较,并以最高匹配度的指纹位置作为待定位目标位置。 本文提出一种基于步长r的室内采样点选取方案,假设选定的定位区域为正方形,如图4所示,在正方形中心设置一个采样点A1,另外分别放置两个采样点A2和A3构成边长为r的正三角形。当初始采样点确定后,以顺时针方向进行转动,当第一层转动完成之后,位于中心位置的采样点A1继续向第二层转动,3个采样点重复第1层的转动步骤逐层外移,直到形成的正六边形恰能覆盖整个监测区域[16],如图4所示。获得定位区域内的所有采样点,遍历所有采样点便可得到l个指纹,每个采样点的指纹利用2.1节方法进行处理后,保存入库,即如公式(8)所示,同时记录每个指纹到达AP的距离Dl。 图4 采样点选取方案 (8) (9) 最终指纹数据库包括:距离Dl、指纹对应的位置loc、采样点的指纹FP。 此方案中r值选取与具体的定位区域大小有关,r值越小采样点数量就越多定位精度越高,反之采样点越稀疏定位精度越差。但是采样点越多,构建指纹地图所需要的代价也越高,同时会造成很大的模糊度,一般几十米内的定位区域内取值为1~2 m[7-8,17]。 在线阶段指纹匹配过程中引入了距离的限制,计算出待定位目标与AP的距离,将要匹配的指纹限定在距离Dl上,缩小指纹匹配范围,提升指纹匹配速度。 2.3.1距离的计算 通常,采用公式(10)所示的路径损耗模型[18]进行距离计算: (10) d=p1×RSS3+p2×RSS2+p3×RSS+p4 (11) 其中,d表示采样点与AP之间的距离,单位m;RSS表示采集信号强度,单位为dBm,p1、p2、p3以及p4为拟合所获参数,值为:p1=-0.00014、p2=-0.00767、p3=-0.1662、p4=-1.112。 图5 信号强度与距离的拟合曲线 图中纵坐标表示距离,单位m;横坐标表示信号强度,单位dBm。此测距模型相比于自由空间衰减模型可以准确反映当前信号的衰减情况。 2.3.2指纹匹配 根据ASPM方案计算出待定位目标和AP之间的距离d后,从指纹数据库中匹配出与距离d最近的点,将待匹配的指纹数据库范围缩小至某一个指纹采样点Γ上,其采样点Γ到达AP的距离DΓ与待测目标到AP的距离d最近。Γ满足: (12) 然而ASPM模型存在误差,所以依据最近采样点计算出的目标位置存在较大偏差,因此将待匹配的指纹数据库匹配范围扩大至[DΓ-low,DΓ+high](low和high值选取和ASPM模型误差有关),将一个匹配点变为多个,提升匹配度。 从指纹数据库中搜索出距离[DΓ-low,DΓ+high]对应的指纹记录Fs=(F1,F2,…,Fs),假设待定位目标检测到AP信号强度为RSSU,将待测目标测得的信号强度RSSU与Fs指纹进行匹配,即计算RSSU与Fs指纹的欧式距离。 (13) 然后对这些距离进行升序排序,取前k个与待测目标指纹欧氏距离最小的指纹,将这些指纹对应的位置坐标求平均作为待测目标的位置,如公式(14)所示: (14) 此方法,待测目标与指纹库匹配时无需和指纹库中所有的指纹进行对比,因此降低了指纹的匹配时间,提高了效率。 指纹匹配算法: (1)输入FPl,RSSU,Dl,Dmax (2)计算待测目标到达AP的距离du ∥p1、p2、p3、p4拟合参数,RSSU表示待测目标的指纹 fori=1 tol∥l表示指纹数量 (3)计算指纹库中与待测目标最近的采样点Γ∥Γ∈(1,2,…,l) end for (4)在Γ采样点基础上扩大指纹匹配范围 Ds=(Ds|low-DΓ if low-DΓ<0 low-DΓ=0 end if ifDΓ+high>Dmax DΓ+high=Dmax∥Dmax表示定位区域内采样点到AP的最大距离 end if fori=1 tos (5)待测目标与距离Ds所对应的指纹匹配方法 d=norm((FP(:,S)-RSSU),2) end for d1=sort(d)∥对d值进行升序排列 d2=d1(1:k)∥d2表示前k个最小的欧式距离 (6)取出前k个指纹对应坐标的平均值作为待测目标位置 forj=1 tok index(j)=find(d==d2(j)) Loc(j,:)=FP(index(j)) end for UL=sum(Loc)/k∥待测目标位置 为了验证算法的性能,在MATLAB2016a编程工具下对算法进行仿真分析,仿真过程中所使用的RSS信号均来源于真实环境测试。测试地点选在教学楼的走廊进行,面积20 m×2.4 m。这个区域,人员走动频繁,干扰复杂,AP放置于走廊两侧,采用图6所示的采样点方案,r取值为2 m,在AP左右侧各选择25个采样点,共计50个采样点。 为了克服RSS信号本身的不稳定性即环境的变动带来的影响,体现信号的统计规律,本文在每个采样点处连续采集100个数据,将采集到的RSS数据取绝对值后映射到二维平面,为了接近原始数据分布,将100个数据点的x轴坐标除以10000,如图7所示。 图6 采样点布置方案 图7 节点分布图 以图7中100个节点为例,然后计算出局部密度ρi和距离δi,其决策图如图8所示。决策图中同时具有较大ρ值和δ值的点恰好是图7中所示数据的聚类中心。此外,δ值很大,但ρ值很小的数据点在原始数据点中是“离群点”。 图8 决策图 3.3.1标准测距模型性能分析 本文在指纹匹配的过程中用到了测距模型,为了验证测距模型的准确性,分别距离AP为2 m、4 m、6 m上随机选3个点,在每个采样点连续采集100次,然后采用公式(11)计算得到距离d,测量结果如图10所示。可以发现,图中线条波动比较剧烈,这是因为无线信号的不稳定,导致计算结果有一定的差异。当待测目标距离AP为2 m时,测量距离的平均值为1.95 m,接近于真实距离;待测目标距离AP为4 m时,测量距离的平均值为4.86 m;待测目标距离AP为6 m时,测量距离的平均值为5.57 m。因此,该测距模型的平均测距误差控制在1 m以内。 图9 聚类结果图 图10 ASPM测距结果值 ASPM测距模型的误差累计密度函数分布如图11所示。从图中可以看出在100次测量中90%以上的结果误差可以控制在2.5 m以内,且距离AP越近误差越小,距离AP为2 m以内的误差大概0.5 m左右。本文在指纹匹配的过程给出了由于测距误差导致指纹匹配失败方法,因此,容许测距有一定的误差,那么在2.3.2节中的low和high取值为2.5。 图11 ASPM误差的累计概率函数 根据经典测距模型,如公式(10),分别计算距离AP 2 m、4 m、6 m上随机3个点的测距结果,测距结果如图12所示。公式(10)中的d0取值为1 m,室内路径损耗系数n=3。 图12 公式(10)测量结果值 图12中当待测目标距离AP为2 m时,测量距离的平均值为1.15 m;待测目标距离AP为4 m时,测量距离的平均值为2.86 m;待测目标距离AP为6 m时,测量距离的平均值为2.78 m。经典测距模型的误差累计密度函数分布如图13所示,在100次测量中距离AP为4 m远时60%的结果误差可以控制在2.5 m以内,距离AP为6 m远时只有30%的结果误差可以控制在3 m内,距离AP为2 m以内的节点误差控制在1 m左右。从图11和图13中可以看出随着距AP的距离增加,两种测距模型的累计误差概率都在增大,但本文提出的ASPM测距模型的准确率要优于其他方法。 图13 经典测距误差的累计概率函数 3.3.2改变测距模型参数对测距结果的影响 当把不同环境下测得的ASPM模型应用于本次实验中,对定位性能会有一定的影响,如图14所示。 图14 改变测距模型参数后得到的测距结果 其中图14(a)是对原始模型参数的微调,与图10相比整体误差变化不是很大;图14(b)是在寝室楼走廊测得的模型参数,用于教学楼走廊试验,误差变化超过10 m,因此要根据实际环境来建立测距模型。 图15是平均定位误差的变化情况,随AP数量增加,本文方法ALCCE与KNN、WKNN定位算法的平均定位误差逐渐变小。当定位区域只有1个AP时,指纹定位算法无法进行定位[7],根据本文的采样点布置方案可以实现定位。 图15 随AP数量增加平均定位误差的变化 随着AP数量增加,定位误差并不一定变小,因为待定位节点可能会选取距离较远的AP,如距离较远,信号较弱,RSS数值较小,受环境影响严重,不利于定位。 参数k是确定ALCCE定位算法所使用的近邻数,当AP=10,平均定位误差与k之间的关系如图16所示,此图的测量结果是100次仿真的平均值。因为随k值变大,定位所需的近邻数变多,平均定位误差也会整体变小。但经过大量仿真发现k值并非越大越好,如果k值很大,会把对称的采样点或距离待定位目标很远的采样点纳入到近邻数中,进而引起较大波动反而会影响定位结果。从图16中可以看出k取6时平均定位误差相对最小。 图16 平均定位误差随参数k的变化 ALCCE算法的时间复杂度由两部分组成,即CFSFDP的时间复杂度和在线阶段指纹匹配时间复杂度。假设定位区域内有N个采样点,每个采样点采集的RSS数据为n个,移动目标节点为M个,则ALCCE算法的时间复杂度为O(n2)。 证明:利用CFSFDP算法对采样点数据进行聚类时,首先计算参数ρi,dij,δi,时间复杂度均为O(n2);其次,节点需要计算其作为簇首时的ci,时间复杂度为O(n);然后,计算每个簇内包含的节点nqi,时间复杂度为O(n)。因此,CFSPDF的时间复杂度为: O(n2+n2+n2+n+n)=O(n2) (15) 在线指纹匹配过程中,移动目标定位时需要和离线指纹库的数据进行匹配,首先要计算距离AP距离,时间复杂度为O(M);其次,移动目标根据计算得到的距离将搜索范围缩小至Ds=(Ds|low-DΓ O(M+s×M)=O(M) (16) 根据以上分析,由于n≫M,因此整个算法的时间复杂度为O(n2)。 本文针对现实Wi-Fi环境中由于RSS信号的不稳定性,提出了一种基于CFSFDP分类的自适应定位算法。该算法首先对采集的指纹数据使用CFSFDP进行预处理,作为位置指纹数据,在此基础上建立离线阶段的指纹地图方案,在线阶段将建立的自适应测距模型和指纹方案相结合,以降低指纹匹配次数。实验表明本文提出的算法具有更好的性能,降低了定位误差,并且在只有1个AP的情况下也可实现定位。但本文采用的算法还不能很好实现对AP的挑选,下一步将研究其自适应的AP挑选方法,为进一步定位求精做准备。 [1] 金培权,汪娜,张晓翔,等.面向室内空间的移动对象数据管理[J]. 计算机学报,2015,38(9):1777-1795. Jin Peiquan,Wang Na,Zhang Xiaoxiang,et al. Moving object data management for indoor spaces[J].Chinese Journal of Computers, 2015,38(9):1777-1795.(in Chinese) [3] Schmidt E, Akopian D. Indoor positioning system using WLAN channel estimates as fingerprints for mobile devices[C]∥IS&T/SPIE Electronic Imaging, International Society for Optics and Photonics 2015: 94110R-94110R-9. [4] Kaemarungsi K, Knshnamurthy P. Modeling of indoor positioning systems based on location fingerprinting[C]∥Proceedings of the 23rdAnnual Joint Conference of the IEEE Computer and Communications Societies.Los Alamitos,USA,2004:1012-1022. [5] Li Qiyue, Li Wei, Sun Wei. Fingerprint and assistant nodes based Wi-Fi localization in complex indoor environment[J].IEEE Journals & Magazines,2016,4:2993-3004. [6] Zhang Wei, Hua Xianghong, Yu Kegen. Domain Clustering Based WiFi Indoor Positioning Algorithm[C]∥2016 International Conference on Indoor Positiong and Indoor Navigation(IPIN).2016:1-5. [7] 李华亮,钱志鸿,田洪亮.基于核函数特征提取的室内定位算法研究[J].通信学报,2017,38(1):158-167. Li Hualiang, Qian Zhihong, Tian Hongliang. Research on indoor localization algorithm based on kernel principal component analysis[J].Journal of Communications, 2017,38(1):158-167. (in Chinese) [8] 田洪亮,钱志鸿,梁萧.离散度WKNN位置指纹Wi-Fi定位算法[J].哈尔滨工业大学学报,2017,49(5):94-99. Tian Hongliang, Qian Zhihong,Liang Xiao. Discrete degree WKNN location fingerprinting algorithm based on Wi-Fi[J]. Journal of Harbin Institute of Technology, 2017,49(5):94-99. (in Chinese) [9] Chai X Y,Yang Q.Reducing the calibration effort for probabilistic indoor location estimation[J].IEEE Trans Mobile Computing,2007,6(6):649- 662. [10] Jin Y Y,Soh W S,Wong W C.Error analysis for fingerprint-based localization[J].IEEE Communications Letters,2010,14(5):393-395. [11] Lee M Y,Han D S.Voronoi tessellation based interpolation method for wi-fi radio map construction[J].IEEE Communications Letters,2012,16(3):404- 407. [12] 王磊,周慧,蒋国平.基于WiFi的自适应匹配预处理WKNN算法[J].信号处理,2015,31(9):1067-1074. Wang Lei, Zhou Hui, Jiang Guoping. WiFi-based Self-adaptive Matching and Preprocessing WKNN Algorithm[J].Journal of Signal Processing, 2015,31(9):1067-1074. (in Chinese) [13] Kuo S P,Tseng Y C.A scrambling method for fingerprint positioning based on temporal diversity and spatial dependency[J].IEEE Trans Knowledge and Data Engineering,2008,20(5):678- 684. [14] Davide Dardari,Andrea Conti,Ulric Ferner.Ranging with ultrawide bandwidth signals in multipath environments[C]∥IEEE Journal & Magazines, 2009, 97(2):404- 426. [15] Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191):1492-1496. [16] 史庭俊,桑霞,徐力杰.WSN中一种基于移动锚节点的节点定位算法[J].软件学报,2009,20(Supplement):278-285. Shi Tingjun, Sang Xia, Xu Lijie.A localization algorithm in wireless sensor networks with mobile anchor nodes[J].Journal of Software, 2009,20(Supplement):278-285. (in Chinese) [17] 赵聘,陈建新.利用现有无线局域网进行室内定位算法研究[J].信号处理,2014,30(11):1413-1418. Zhao Pin,Chen Jianxin.A study on indoor localization algorithm using existing wireless local area network[J]. Journal of Signal Processing, 2014,30(11):1413-1418.(in Chinese) [18] Zhuang Y, Li Y, Lan H.Smartphone-based WiFi access point localization and propagation parameter estimation using crowdsourcing[J].Electronics Letters, 2015,51(17):1380-1382.





2.2 室内采样点选择方案

2.3 在线位置指纹的处理
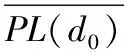
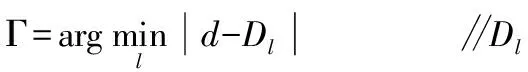
3 实验分析
3.1 实验设置
3.2 指纹聚类对算法的影响



3.3 ASPM测距模型性能





3.4 AP数量对定位的影响

3.5 参数k对定位性能的影响

3.6 算法时间复杂度分析
4 结论

