考虑降雨入渗的隧道变形及支护受力数值分析

郭昱葵， 马启和， 郭震山

(1. 中交第二公路勘察设计研究院有限公司， 湖北 武汉 430056; 2. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074; 3. 山西省交通科学研究院 岩土与地下工程山西省重点实验室， 山西 太原 030006)

隧道施工中，由降雨引起的雨水入渗不仅会导致土体含水率和孔隙水压力上升，使土体自重增加，而且会使土中基质吸力和土体强度参数随含水率的增大而明显减小，进而降低土体的抗剪强度，破坏隧道围岩原有的稳定状态，可能使隧道支护体系产生过大的变形和内力，严重时使支护结构开裂破坏，工程安全性大大降低。因此，探讨降雨入渗对隧道变形及支护结构受力特性的影响规律具有非常重要的意义。

降雨过程中的雨水渗透大都为非饱和渗流，而非饱和土中的渗流问题一直是岩土工程研究中的热点和难点问题[1,2]。目前，国内外学者在非饱和土的性状及非饱和渗流方面已进行了相关研究。Fredlund等[3]针对非饱和土强度计算公式，在饱和土的摩尔库伦抗剪强度公式基础上考虑基质吸力的影响，得到了非饱和土的计算公式。包承纲等[4,5]以基质吸力为中心，结合实际工程问题讨论了非饱和土的性状。朱伟等[6]通过归纳总结，从力学角度探讨了几个非饱和土体渗流的基本问题。吴宏伟等[7,8]指出降雨入渗对工程安全有较大威胁，研究降雨入渗问题具有很重要的理论和工程应用意义。

然而，现有文献主要集中于对边坡在降雨入渗过程中变形及破坏形态的研究[9～11]，而鲜有文献研究降雨对隧道变形及支护受力的影响。另外，在数值模拟过程中，未能充分考虑降雨入渗过程中基质吸力与土体强度参数随含水率的变化。鉴于此，本文通过采用FLAC3D软件，编制相应FISH(Friendly Interactive Shell)语言将降雨入渗过程中基质吸力及土体强度参数随含水率的变化关系嵌入到计算过程中，对某浅埋膨胀性围岩隧道在降雨入渗过程发生的非饱和渗流进行数值模拟，并对降雨过程中隧道的变形及支护受力进行深入研究。

1 非饱和渗流的数值实现

FLAC3D软件中的流固耦合模块可以完全解决饱和情况下的渗流问题[12]，该计算中非饱和区的孔压被强制设为零，不能考虑基质吸力的作用。然而，在非饱和土体中，基质吸力随含水率的不同而发生明显改变，进而会对土体抗剪强度产生不可忽略的影响[13]。因此，本文使用软件内置的FISH语言编制相应的程序，利用孔隙介质中基质吸力与含水率之间的函数关系(即土-水特征曲线)改变基质吸力。白福青等[14]以南阳膨胀土的实验研究为基础，通过使用滤纸法对土-水特征曲线进行分析，发现了基质吸力与含水率的经验关系为：

lg(hm)=61.473w-0.357

(1)

式中：hm为基质吸力；w为含水率。

同时，考虑降雨增湿过程中隧道围岩的遇水软化现象，将围岩的强度参数(即内摩擦角和黏聚力)与含水率的变化关系嵌入到渗流计算中，实现降雨过程中围岩强度参数随计算时步的实时更新。李丹等[15]以大量的直剪试验数据为基础进行拟合分析，得到膨胀土的强度参数与含水率关系表达式为：

(2)

式中：μc及μf分别为黏聚力和内摩擦角的均值。

本文将基于式(1)，(2)，建立某浅埋膨胀性围岩隧道的数值计算模型，模拟其降雨入渗过程。数值计算流程(图1)为：

图1 数值计算流程

(1)建立计算模型，赋予材料相应的模型参数，设置初始条件及相应的边界条件，并平衡初始地应力；

(2)将地应力平衡后的位移场及速度场清零，并进行隧道的开挖与支护；

(3)打开渗流模块并设置渗流参数及降雨边界条件；

(4)在每一计算时步中，提取节点饱和度值Sr，若饱和度不等于1，则将节点饱和度转化为节点含水率，按照基质吸力与含水率之间的经验公式，求得节点的吸力值，并将其赋值给节点的孔隙水压(负孔隙水压)；若饱和度等于1，则直接进入下一步计算；

(5)通过反距离加权差值法，将节点饱和度转化为单元饱和度，并通过单元含水率求得相应的摩擦角和黏聚力，并将其赋值给该单元；

(6)检测地表节点孔隙水压力p′，若p′>0(达到饱和)，则可通过固定该节点的孔隙水压力(取p′为0)来施加压力边界。

(7)检查是否达到计算终止条件，若未达到则重复步骤(4)～(7)，否则结束计算。

2 隧道非饱和渗流数值模拟

2.1 工程概况

某山岭隧道全长430 m，洞口段埋深8.4 m，是双洞双向行驶分离式浅埋隧道。本文取洞口段进行研究，该区段围岩为V级膨胀性中风化玄武岩。隧道衬砌内轮廓采用半径为5.5 m的单心圆，单洞净宽10.5 m，净高5.0 m。

2.2 数值计算模型及参数

如图2所示，为简化计算，将问题转化为平面应变问题来分析，取模型厚度1 m，宽度100 m，埋深8 m。对模型四周施加法向位移约束，并将底部固定；模型四周、底部均为不透水边界，顶部为降雨边界。模拟过程中，围岩为摩尔库伦模型，其摩擦角和黏聚力在降雨过程中随含水率的变化取值采用文献[15,16]中的试验结果。初期支护厚度为26 cm，采用Shell单元模拟。锚杆沿隧道环向布置，锚杆直径32 mm，长为4 m，采用Cable单元模拟。围岩及支护结构的力学参数汇总于表1。为了研究不同强度降雨对隧道变形及支护结构受力的影响，分别取降雨强度为200，400，600，800，1000 mm/d，并模拟持续降雨50 h。为简化计算，围岩渗透系数均取其饱和渗透系数5.78×10-4cm/s。

图2 隧道数值计算模型

表1 围岩及支护结构力学参数

3 模拟结果分析

3.1 基质吸力及含水率分析

文献[3]基于试验发现非饱和土的抗剪强度可用净法向应力和基质吸力两个应力状态变量来描述，并提出了基于库伦公式的非饱和土强度计算公式：

τf=c′+(σ-μa)tanφ′+(μa-μw)tanφb

(3)

式中：c′为有效凝聚力；φ′为有效内摩擦角；σ为正应力；μa为孔隙气压力；μw为孔隙水压力；σ-μa为净法向应力；μa-μw为基质吸力；tanφb为非饱和土的抗剪强度随基质吸力增加的速率。

从式中可以看出，在非饱和土中，基质吸力对抗剪强度的影响不可忽视。在持续降雨时，雨水入渗使非饱和区土体的含水率显著增加，导致基质吸力明显减小，进而使得土体抗剪强度下降，导致隧道围岩原有的稳定状态受到扰动；同时隧道上覆岩体含水率增加，开挖面上覆压力增大，支护结构受力变形增大，工程安全性降低。因此，对降雨条件下土体含水率及基质吸力随降雨历时变化规律的分析有着重要工程意义。

图3为降雨强度600 mm/d工况下地表处土体含水率与基质吸力随降雨历时的变化曲线。从图中可看出，地表含水率变化与降雨历时基本成线性关系；降雨前期土体入渗率较大，雨水全部自地表入渗，此时地表含水率增长速度较快并与降雨历时呈线性正相关；当降雨历时进一步增加时，雨水入渗率随之降低，地表由于雨水入渗率降低到小于降雨强度而出现积水，此时地表土体达到饱和，降雨50 h后地表处含水率达到33.87%，接近其饱和含水率(34.19%)。同时，图中还显示：基质吸力在降雨初期减小速度较快；当降雨历时进一步增加时，基质吸力减小速度逐渐缓和，最终趋于平稳，持续降雨50 h后，地表处基质吸力由初始的151.90 kPa减小到9.69 kPa。

图3 地表基质吸力及含水率随降雨历时变化曲线

图4为降雨前土体初始含水率及孔隙水压力分布的等值线云图。初始土体含水率及孔隙水压力沿深度方向呈线性分布，地表处土体较为干燥，含水率较低，基质吸力最大。图5～7分别为降雨强度600 mm/d工况下持续降雨10， 30， 50 h后土体含水率及孔隙水压力分布的等值线云图。图中显示：当降雨持续时间增加时，浸润锋线不断向土体深处移动，降雨50 h后浸润锋线推进到约15 m深位置处，在浸润锋线的深度范围内，土体的含水率和孔隙水压力都有所增大。相同降雨时间下，地表处含水率增加量最大，浸润锋线以下土体含水率基本不变。

图4 初始含水率与孔隙水压力分布云图(降雨强度=600 mm/d)

图5 降雨10 h后含水率与孔隙水压力分布云图(降雨强度=600 mm/d)

图6 降雨30 h后含水率与孔隙水压力分布云图(降雨强度=600 mm/d)

图7 降雨50 h后含水率与孔隙水压力分布云图(降雨强度=600 mm/d)

3.2 拱顶沉降分析

图8为不同降雨强度下，隧道拱顶沉降随降雨持续时间的变化曲线。从图8可以看出，降雨初期隧道拱顶沉降并无明显变化；当降雨持续一定时间后，拱顶沉降开始显著增加。分析其原因：雨水入渗的影响深度在降雨初期较小，隧道围岩强度及土中基质吸力的减小并不明显，围岩仍具有较好的自支护能力。当降雨历时进一步增加时，浸润锋线不断向土体深处移动，即向拱顶发展。当降雨持续时间达到一定程度时，浸润锋线接近拱顶，在浸润锋线范围内，围岩中基质吸力随含水率的增大而显著减小，进而使土体强度显著降低，极大地削弱了围岩承载能力，导致拱顶沉降显著增加。此外，从图8可以看出：拱顶沉降随降雨强度的增加而明显增大，但是当降雨强度增大到一定程度(600 mm/d)后，拱顶沉降对降雨强度变化的敏感性减弱。分析其原因：当降雨强度较小时，雨水入渗率小于土体的饱和渗透系数，因此降雨过程中的雨水全部入渗，拱顶沉降基本随降雨强度线性增加；当降雨强度增大到某一值后，部分雨水来不及入渗，不久将会在地表形成积水，这部分积水将以地面径流的方式排走，此时雨水入渗率与土体的饱和渗透系数相等，因此此时拱顶沉降与降雨强度关系不大。降雨前隧道拱顶沉降为14.59 mm，各降雨强度下，降雨结束后拱顶沉降依次增大至15.79，17.33，18.44，19.10，19.56 mm，相比于降雨前分别增加了8.22%，18.77%，26.39%，30.91%，34.06%。显然，长时间的强降雨对隧道围岩变形和稳定的影响较大。

图8 拱顶沉降随降雨历时变化曲线

3.3 初期支护弯矩分析

图9为不同降雨强度下隧道初期支护最大弯矩随降雨历时的变化曲线。其中，各工况下初期支护的最大弯矩均出现在边墙与仰拱交界处。与拱顶沉降的变化规律相似，即在降雨初期，初期支护弯矩基本不变，降雨持续一定时间后，初期支护弯矩突然增大，最终趋于稳定。初期支护弯矩随降雨强度的增加而明显增大，但是当降雨强度增大到一定程度(600 mm/d)后，初期支护弯矩随降雨强度变化不再明显并逐渐趋于稳定。降雨前初期支护最大弯矩为24.83 kN·m，各降雨强度下，降雨结束后，初期支护最大弯矩依次增大至25.83，27.89，29.37，29.95，30.24 kN·m，相比于降雨前分别增加了4.03%，10.31%，18.28%，20.62%，21.79%。可见，长时间的强降雨对初期支护的弯矩影响很大。

图9 初期支护最大弯矩随降雨历时变化曲线

3.4 锚杆轴力分析

图10为不同降雨强度下锚杆最大轴力随降雨历时的变化曲线。同样地，各工况下锚杆最大轴力值均出现在边墙与仰拱交界处。从图中可看出，在降雨初期，锚杆轴力基本保持不变，随着降雨时间的增加，锚杆的最大轴力反而变小。此外，随着降雨强度的增大，锚杆轴力同样减小。分析其原因：锚杆主要是通过与周围岩土体之间的黏结摩擦作用发挥功效，降雨导致锚杆锚固段土体软化，对锚杆的粘结锚固作用减弱，锚杆轴力减小。

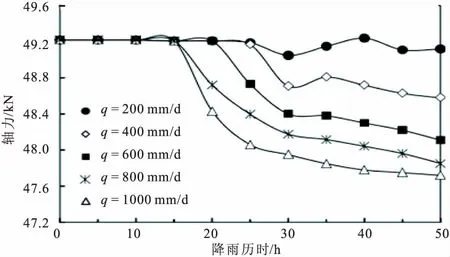
图10 锚杆最大轴力随降雨历时变化曲线

4 结 论

本文通过采用FLAC3D软件，编制相应的FISH语言程序将降雨入渗过程中基质吸力及土体强度参数随含水率的变化关系嵌入到计算过程中，对围岩隧道在降雨入渗过程中发生的非饱和渗流进行数值模拟，研究了不同降雨强度下隧道变形及支护受力的变化规律，得到以下主要结论：

(1)随降雨历时的增加，浸润锋线不断向土体深处移动，在浸润锋线的深度范围内土体的含水率逐渐增加，基质吸力降低；降雨持续一定时间后，地表土体含水率接近饱和，基质吸力趋于零。

(2)降雨初期，隧道拱顶沉降以及初期支护弯矩随降雨历时的变化并不明显；当降雨持续一定时间，浸润锋线接近拱顶时，拱顶沉降及初期支护弯矩均显著增加。降雨对锚杆轴力影响不大，当降雨历时增加时，围岩有所软化，对锚杆的粘结锚固效果减弱，锚杆轴力减小。

(3)当降雨强度较小时，隧道拱顶沉降和支护受力随降雨强度增加变化明显；当降雨强度增大到一定值后，此时雨水入渗率与土体饱和渗透系数相等，拱顶沉降和支护受力随降雨强度的增加变化较小并逐渐趋于稳定。