地连墙基坑逆作开挖的动态规划

曹 净， 杨泽帅， 高 越， 汪 尺， 刘海明

(昆明理工大学 建筑工程学院， 云南 昆明 650500)

由于基坑开挖过程中考虑时空效应及开挖土体工程性状的不确定性，基坑开挖存在动态施工力学中开挖参数优化的问题[1,2]。在大城市地下空间的开发过程中，由于土地资源稀缺，场地范围狭窄，随着开挖深度的不断增加，基坑支护工程成为热点与难点问题[2～4]。为了实现基坑稳定性及变形的可控，常采用地连墙与逆作法相结合的施工方案。许多学者的统计研究表明基坑失事的主要原因是施工因素[5～8]，其中施工工序不合理造成基坑事故的概率很大。因此，地连墙支护方案下研究基坑逆作开挖参数的动态规划十分重要。鉴于目前大部分的规划方法均有一定的适用范围且偏于基坑支护结构设计的优化，本文针对基坑开挖参数的优化问题，引入响应面-枚举法来研究地连墙基坑逆作开挖参数的动态规划。

目前大部分基坑开挖平面的近似长宽比大于2，若按实际三维单元建立模型，单元个数和计算量十分庞大，可以合理简化三维模型，采用二维平面应变模型。因此将规划问题简化为对地连墙基坑二维剖面上逆作开挖参数的规划。

1 建立规划模型

一个规划问题可以作如下描述[9]：

存在一组由可变参数组成的n维向量X=[X1，X2，…，Xn]T∈En，实际问题变量X1，X2，…，Xn称为决策变量。目标函数f(X)与不等式约束函数gi(X)、等式约束函数hj(X)均是关于决策变量的函数。约束条件为：

(1)

式中：p为不等式约束个数；q为等式约束个数；n，p，q之间是相互独立的，无任何关联。在约束条件下，求解maxf(X)或minf(X)，使目标函数极大或者极小，求解值便是规划问题中决策变量的最优值。

1.1 决策变量

决策变量是规划过程中可进行调整且调整后会导致设计方案结果改变的独自变量。

基坑变形与开挖过程关系密切，相同支护设计条件下的同一基坑若采用不同的开挖方式，将对基坑变形产生不同程度的影响，有时候基坑变形的差异会很大[2]。而开挖方式由多个开挖参数组成和影响，所以开挖参数是开挖动态规划的决策变量。

对于基坑逆作开挖，由于一柱一桩施工于土方开挖前，为了不增加开挖难度，分块长度按照柱间距选取，故不把分块长度作为决策变量。地连墙基坑二维剖面上逆作开挖的参数主要有分层厚度和各区域开挖顺序。基坑采用直角坐标系，先将选取的二维剖面定义为x-z平面，二维剖面上基坑宽度方向为水平x轴方向、深度方向为竖向z轴方向，再将基坑长度方向定义为直角坐标系中的y轴。

1.1.1分层厚度

合适的分层厚度有利于施工工况与设计工况相一致，减少基坑变形。为满足单层开挖边坡的稳定性，其开挖厚度一般为2.0～5.0 m[10]。普琼香[11]在放坡基坑开挖的动态规划研究中，考虑施工机械的可操作性及全深度范围放坡基坑分层开挖的要求，将开挖分层厚度范围控制在1.0～4.0 m内进行动态规划。对于5.5 m基坑，优化后的分层厚度为2.75 m；对于3.5 m基坑，优化后的分层厚度为1.75 m。综合考虑，地连墙支护基坑剖面深度z轴方向上的分层范围取值为1.5～3.0 m。

因逆作法中架设地下室梁板模板所需的设计标高限制了分层厚度的取值，所以综合考虑先按1.5～3.0 m的分层范围将架设地下室梁板模板所需设计标高间高差最大的深度进行分层，其余区域的深度则按选定的分层厚度分别分层。

1.1.2各区域开挖顺序

分层厚度与一柱一桩的间距将剖面土方开挖部分划分成若干块小区域，采用不同的开挖顺序开挖各小区域，会造成不同的应力释放路径，带来较大差异的变形。合理的卸载顺序，不仅基坑变形得到了控制而且基坑开挖对周围环境的影响也有所减小。

考虑对称开挖，则各区域的开挖顺序可以分为剖面岛式开挖与剖面盆式开挖两种。剖面岛式开挖是先按分块长度开挖基坑周边两侧单块区域，再开挖基坑内部多块区域，以分层开挖的方式完成土方施工，如图1所示。而剖面盆式开挖是先按分块长度开挖基坑中部多块区域，再开挖基坑周边两侧单块区域，同样以分层开挖的方式完成土方施工，如图2所示。其中在开挖过程中相邻区域开挖面之间的高差不大于3 m[2]。

图1 剖面岛式开挖示意

图2 剖面盆式开挖示意

由于地连墙支护下基坑逆作开挖首先施工周围地下连续墙和建筑物内部的一柱一桩，然后开挖土方至架设顶板模板所需的设计标高后施工顶板，再开挖下部土方至架设楼板模板所需的设计标高后施工楼板。依此类推从上而下开挖土方并施工地下室主体结构，同时已经完成施工的地下室梁板可作为基坑的临时支撑。所以地下室楼板的设计标高会影响基坑逆作开挖的工况，导致逆作基坑在二维剖面上被地下室楼板的设计标高分为多层区域。针对基坑的每层区域，只考虑盆式开挖或者岛式开挖两种开挖顺序。

1.2 优化目标

优化目标是进行规划后欲到达的目的，一般用来评价优化设计方案优劣的标准，通常把一些经济指标或者技术指标定为优化目标。

规划基坑土方开挖方式的施工方案时要求基坑支护体系按实际设计的选取以确保基坑稳定性，因此既定的基坑支护体系下基坑开挖土方量也是一定的。另外，土方开挖的工程造价涉及施工机械租赁和施工人员工资等情况，不宜准确掌握。最终选择土方开挖的工期作为优化目标。

1.3 目标函数

目标函数是反映优化设计方案目标和变量之间的关系函数。针对目前较多的深基坑，一般土方开挖均采用机械施工，所以仅考虑以施工机械的施工效率来确定土方开挖的工期和开挖参数间的关系函数。

施工机械数量N已定，不考虑下雨停电等不可抗力因素，可按下式计算区域i的工期ti[12]：

(2)

式中：Qi为区域土方量(m3)；KC为土质变化的时间影响系数；Pi为挖掘机生产率(m3/台班)；C为每天工作班数，采用两班倒的上班模式；K为时间利用系数(一般取值0.8～0.9)。

其中按每台班正常工作8 h来计算挖掘机的生产率Pi[13]：

(3)

式中：q为挖土机斗容量(m3)；n为每小时内工作循环次数，见表1；KH为铲斗的充盈系数，见表2；KS为土的最初可松性系数；KB为工作时间利用系数(一般取值0.7～0.85)。

表1 铲斗的充盈系数KH取值

注：反铲不用考虑铲斗的充盈系数，当采用反铲时KH取1

表2 每小时内工作循环次数n取值

而区域土方量是关于开挖参数Xj的函数Qi=Qi(Xj)，所以反映优化目标工期T和决策变量开挖参数之间的目标函数可表示为：

(4)

式中：t1为中间土体采用盆式开挖时所需工期(台班)；t2为两边土体采用盆式开挖时所需工期(台班)；t3为中间土体采用岛式开挖时所需工期(台班)；t4为两边土体采用岛式开挖时所需工期(台班)；l为挖掘机在循环作业外的行驶路程(m)；v为挖掘机行驶速度(m/s)，N为施工机械数量。

挖掘机在循环作业外的行驶路程也是关于开挖参数Xj的函数l=l(Xj)，再结合式(2)可得到目标函数为：

(5)

1.4 约束条件

约束条件是规划过程中为了使优化设计方案可行而必须满足的各种限制条件。规划地连墙支护基坑土方开挖参数的施工方案时要求基坑支护体系按实际设计来支护以确保基坑稳定性，所以不考虑支护结构稳定性的影响，直接选取变形约束来作为规划约束条件。

逆作法施工地下结构时，控制一柱一桩与地连墙的不均匀沉降是施工过程中的关键技术之一，其中合理的土方开挖流程则是控制不均匀沉降的主要措施[14]。此外，基坑支护结构的水平位移是反映支护结构工作状况的直观数据[15]。因此，地连墙基坑逆作开挖动态规划中，选取地连墙墙顶水平位移、相邻一柱一桩间差异沉降以及地连墙与边柱间差异沉降作为约束条件。

2 运用响应面-枚举法规划开挖参数

响应面-枚举法分为两个部分，第一部分是先通过均匀试验设计构造响应面输入数据，然后通过数值模拟参考约束条件得到输出数据，最后将输入和输出数据进行非参数回归(Alternating Conditional Expectations，ACE)得到响应面。第二部分是依据目标函数和约束条件关于决策变量的转换关系采用枚举法进行开挖参数的规划。

2.1 设计均匀试验确定输入数据

首先，采用方幂法构造均匀表Uniform Table，简称U表。其整体表达式为Un(Ns)，其中n表示试验次数、N表示试验水平数、s表示试验因素数。每个均匀表为一个n×s的矩阵，要求n列中的每一列是{1,2,…,n}的置换，而s行中的每一行是{1,2,…,n}的子集。

其次，以中心化L2-偏差CD2为均匀表的度量[16]选择出均匀性最好的试验水平组合。

最后，根据使用表进行规划模型中决策变量的均匀试验设计[9]。模型中有s个决策变量即存在s个因素，分别定义为X1,X2,…,Xs，其中根据决策变量的取值范围将每个因素的取值范围确定为[Xjmin,Xjmax]j=1,2,…,s，而Xjmin和Xjmax分别为第j个因素可能的最小值和最大值。根据试验次数将每个因素等分为n个水平即N=n，

(6)

式中：i为水平序号，i=1,…,2…,n；j为因素序号，j=1,…,2…,s；Xij为水平i下第j个因素的取值。由计算出的Xij得到一个n×s的矩阵即为输入样本表。

2.2 模拟动态开挖确定输出数据

通过输入样本表确定各水平下模型的开挖参数后采用MIDAS/GTS软件建立各个模型进行基坑土方动态开挖的模拟。输出数据则是通过数值模拟并参考约束条件得到。

近几年在深基坑工程动态开挖模拟的研究中，大部分学者只按常规开挖顺序分施工工况直接模拟基坑开挖，并没有考虑施工过程中的动态变化[17,18]。随着深基坑研究的发展，有学者开始考虑开挖顺序的影响，不过只是简单地比较了同一断面两种不同开挖步序的优越性，不具有普遍性也没有达到优化的要求[18]。此外还有学者在基坑施工过程的三维模拟分析中，采用与实际情况相同的起伏岩、土层面进行计算，更真实地模拟了基坑支撑体系的状态[19]。只是这些研究都没有将每个工况的施工进行分区分段的细化模拟，没有考虑土方开挖过程中的动态变化，没能真正地模拟基坑开挖过程中围护墙位移和地下室桩柱结构差异沉降的动态变化。

为了与实际开挖过程相接近，本文在模拟基坑开挖过程时是按照基坑开挖参数来将开挖范围内的土体划分为多个小矩形，以此来模拟每次开挖的范围。

2.3 基于ACE非参数回归响应面

采用ACE非参数回归技术[20]将输入数据和输出数据进行回归得到响应面[21]。其中ACE回归技术首先不设定响应面函数形式，而是寻找第i水平下输入数据Xi1，Xi2，…，Xis的映射值φi1(Xi1),φi2(Xi2),…,φis(Xis)和输出数据Yi的映射值φi(Yi)，并使得它们满足如下映射关系：

φi(Yi)=φi1(Xi1)+φi2(Xi2)+…+φis(Xis)+εi

(7)

式中：εi为拟合误差。从而可以确定响应面函数为：

(8)

图3 响应面-枚举法的应用流程

但是当因素数和水平数较多时，进一步拟合求解ψi[·]是十分麻烦的，而且复杂的函数关系在拟合过程中会存在新的拟合误差，为此引进插值算法，基于响应面关系进行插值计算获得相应的输出参数yi。由均匀试验设计得到第i水平下输入数据Xi1，Xi2，…，Xis。每个参数在取值区间[Xjmin,Xjmax]j=1,2,…,s内均有m个计算点且均匀分布，则可以生成较为密集的插值点。对于i水平下第j因素其取值区间内任意一个输入参数xij的映射值φij(xij)可以插值得到：

φij(xij)=interp(Xij，φij(Xij)，xij)

(9)

式中：interp(Xij，φij(Xij)，xij)表示xij关于Xij和φij(Xij)的插值结果。通过响应面关系再得到输出参数yi的映射值φi(yi)为：

φ(yi)=φi1(xi1)+φi2(xi2)+…+φis(xis)+εi

(10)

最后通过再插值得到输出参数yi：

yi=interp(φi(Yi),Yi,φi(yi))

(11)

式中：interp(φi(Yi),Yi,φi(yi))表示φi(yi)关于φi(Yi)和Yi的插值结果。

2.4 基于响应面规划开挖参数

基于上述得到的响应面来规划开挖参数时，采用枚举法，利用计算机运算速度快、精确度高的特点将满足约束条件范围内的参数一一列举，再直接用问题中的条件进行检验。

利用Matlab编程，首先在决策变量的取值范围内产生均匀分布的随机数，并基于响应面通过随机抽样进行计算机仿真模拟，其次重复N次独立随机抽样计算得到大量仿真样本，再以约束条件对仿真样本进行筛选，最后统计优化目标选出最优值并以此确定出对应的开挖参数。

3 实 例

为验证响应面-枚举法的可行性和有效性，选取昆明置地广场周围地下室的逆作C区基坑进行研究。逆作C区基坑采用整体地连墙“两墙合一”+地下结构梁板支撑的支护形式。考虑地连墙墙顶的监测点位置选取1-1剖面进行研究，如图4所示，基坑开挖平面如图5所示。1-1剖面上逆作C区基坑开挖部分由①，④组成，C①区开挖部分z方向深16.5 m，x方向宽18.2 m；C④区开挖部分z方向深16.5 m，x方向宽33.6 m。工程先进行B区的基坑开挖及地下室施工，待主楼T2施工到23层后再进行C区地下室的逆作施工，并且在逆作过程中将B区基坑的支护结构拆除，施工工序如图6所示。由于上述施工工序的原因，运用MIDAS/GTS软件模拟C区基坑的过程中应该考虑B区基坑。整个1-1剖面上涉及的基坑支护结构及建筑主体结构的尺寸如表3，4所示。

图4 1-1剖面/m

图5 基坑平面

图6 二维C区基坑逆作开挖示意/m

表3 逆作C区范围内各结构尺寸及材料m

注：δ为结构厚度；d为结构直径；C为混凝土；Q为钢材

表4 顺作B区范围内各结构尺寸及材料 m

注： B区基坑部分范围内地下室并没有上层建筑，该部分地下室的尺寸及材料取值同表3

3.1 工程条件

忽略各土层中的透镜体，由深层位移监测点G68，Q23，Q08，G31(图5)对应位置处的钻孔ZK215，BK06，BK03，ZK15得到1-1剖面的土层分布情况，如图7所示。

图7 由钻孔得到的土层分布/m

在采用MIDAS/GTS模拟开挖时为满足模型中土层与结构间的耦合，将性质相近的④2粉土和④3粉质黏土概化为同一土层，同时将⑤1粉质黏土概化入⑥1粉质黏土中。此外，基坑底部及以下土层随强风化灰岩面坡向变化，起伏相对较大。为了使模型耦合的同时坡面符合实际走向，则根据起伏趋势将基坑底部及以下岩土层均用阶梯状表示。最终将复杂的土层分布简化为图8，使其既可以满足模型耦合又可以贴近实际变形。

图8 模型中的土层分布/m

此外，虽然实际地下水位随基坑开挖不断变化，但是所研究的开挖参数组合数较多不易模拟地下水，则在模拟基坑开挖的过程中并没有考虑地下水的变化。

其中土层物理力学指标如表5所示：

表5 土层物理力学指标

1-1剖面西侧存在吹箫路和居民住宅，东侧存在北京路。C区基坑开挖动态规划中应考虑的各种荷载如表6所示。

表6 C区基坑逆作开挖过程中的荷载取值

3.2 逆作C区基坑开挖动态规划

3.2.1确定C区基坑决策变量

根据C区基坑逆作开挖的工序，按-3.75，-8.8，-12.3，-15.8 m处的开挖面以及这些开挖面上模板架设的施工情况将深16.5 m的基坑划分为五层区域。为了运用响应面规划方法规划分层厚度和各层区域开挖顺序，将分层厚度转换为分层层数，定义为决策变量X1；同时将每层区域的开挖顺序均转换为岛式开挖深度所占基坑深度的比值，分别定义为决策变量X2，X3，X4，X5，X6。取值区间如表7所示。

表7 逆作C区基坑开挖参数取值区间

3.2.2确定C区基坑目标函数

采用两台型号PC22-8的履带式挖掘机逆作开挖C区基坑土方。该挖掘机的标准斗升容量q=1 m3，KB=0.8，v=4.2 km/h=1.17 m/s。基坑开挖范围位于中部的土层分布较为稳定，且该范围内土体性质相接近均为粉质黏土，因此取KC=1.1，Ks=1.24，K=0.9。此外，采用两班倒上班模式取C=2。施工机械数量N=2已定，可按式(5)得到目标函数T：

+0.02X6

(12)

3.2.3确定C区基坑约束条件

逆作C区基坑选取地连墙G68和G31的墙顶水平位移、相邻一柱一桩间差异沉降以及地连墙与边柱间差异沉降作为约束条件。基坑所需支护深度为16.5 m且土体变形过大对周围环境影响较大，所以约束条件定为：地连墙墙顶水平位移控制值为-30～30 mm；相邻一柱一桩间差异沉降控制值为-20～20 mm；地连墙与边柱间差异沉降控制值为-20～20 mm。

3.2.4确定输入数据

该模型的决策变量为X1，X2，X3，X4，X5，X6，需构造一个6因素的均匀试验表。以中心化L2-偏差CD2为均匀表的度量选择出均匀性最好的试验水平组合，当采用17水平时6因素具有理想的偏离度。以2为元运行均匀表U17×176，删除最后一行，得到16水平的最优试验设计，将6个决策变量在取值区间内均等为16份，并将均匀表U17×176进行组配后确定均匀试验输入样本，如表8所示。

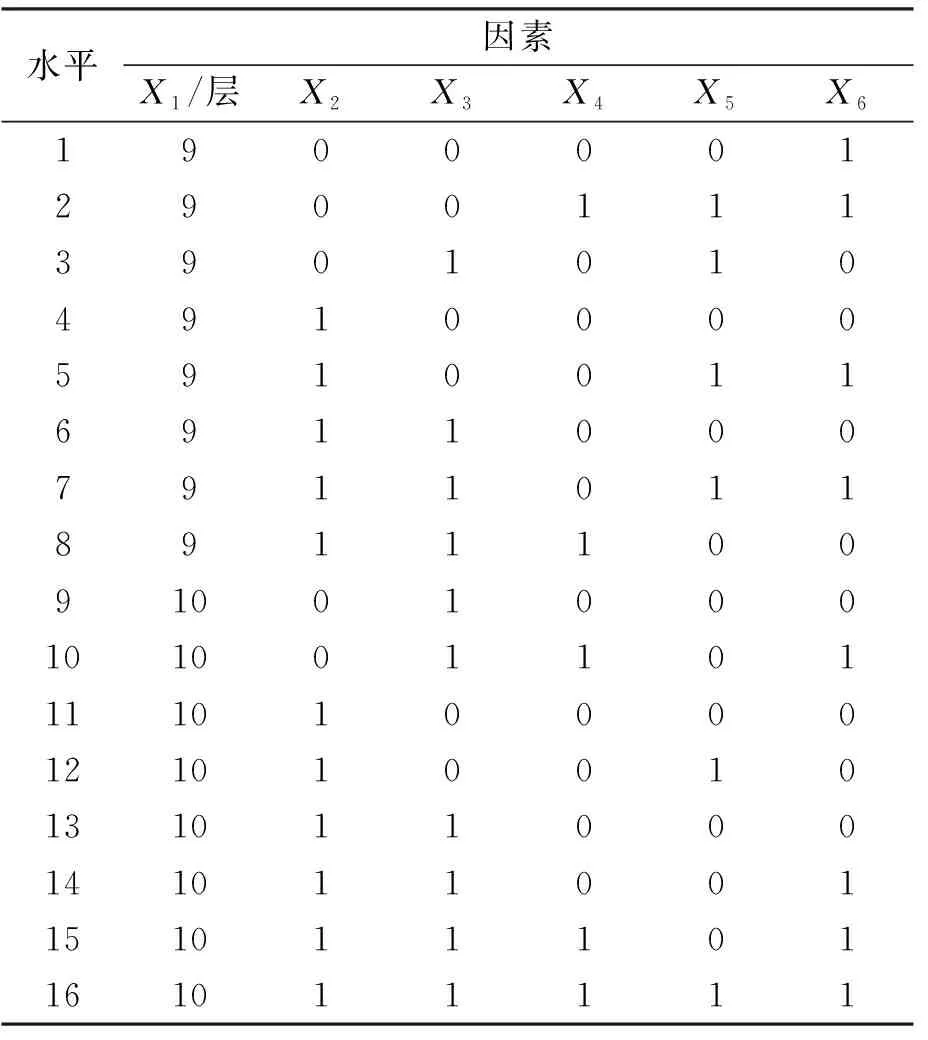
表8 逆作C区基坑输入样本

3.2.5确定输出数据

根据C区逆作施工工况，仅考虑分层厚度和各开挖面范围内土体的开挖顺序来进行该组平行试验。试验采用MIDAS/GTS软件进行模拟，共16次试验模拟。

考虑整个基坑将模拟尺寸确定为z方向深55.8 m，x方向宽331.8 m。根据周围环境，二维模型两侧的边界条件仅限制x方向的位移，底侧的边界条件则限制x，z两个方向的位移。

逆作开挖模型中支护结构的本构为弹性模型，可根据GB 50010-2010《混凝土结构设计规范》得到相关结构材料参数。而岩土体本构采用莫尔-库伦模型，可以根据表4确定土层材料参数。此外，由于模拟的是二维剖面，则根据圆形支护结构及作用荷载的对称性，采用等效梁来模拟原来B区基坑圆形支护结构的空间效应[22]。

分析16个水平下的试验数据得出C区基坑开挖的影响规律，从而确定输出参数。针对逆作法施工的基坑除了应控制地连墙墙顶位移和各一柱一桩沉降外，施工过程中同样应该重视邻柱间的沉降差异及地连墙与边柱间的沉降差异。则根据剖面图4中C区逆作基坑位置的分布情况，选取地连墙G68，G31的墙顶水平位移以及C④范围内1#，3#和C①范围内5#，8#一柱位置处顶板的竖向位移作为观察对象。各个水平下不同位置处变形随开挖步骤的变化曲线如图9～14所示。下面对各个观察对象进行分析，确定输出参数：

图9 各水平下G68墙顶水平位移随开挖变化曲线

图10 各水平下G31墙顶水平位移随开挖变化曲线

图11 各水平下一柱1#位置顶板竖向位移随开挖变化曲线

图12 各水平下一柱3#位置顶板竖向位移随开挖变化曲线

图13 各水平下一柱5#位置顶板竖向位移随开挖变化曲线

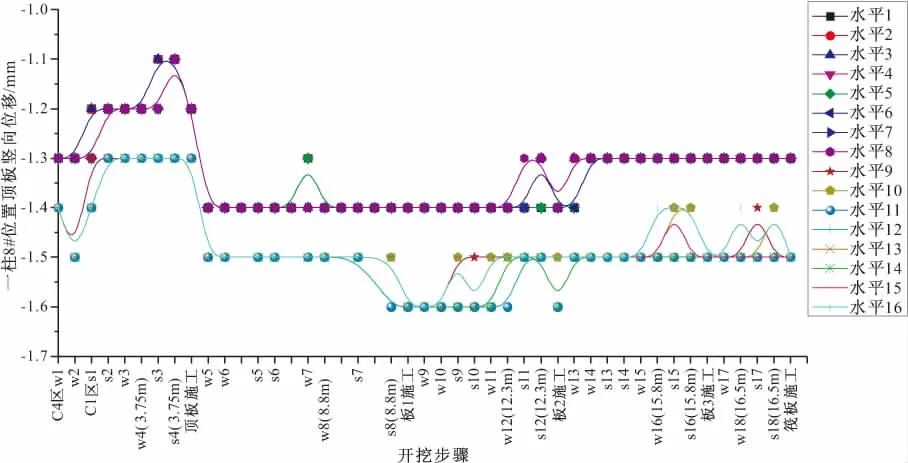
图14 各水平下一柱8#位置顶板竖向位移随开挖变化曲线

图9，10分别为地连墙G68，G31墙顶水平位移随开挖变化的曲线。观察两个图形，各水平下地连墙G68墙顶水平位移均随着基坑开挖不断增加，且C④区的土方开挖顺序对G68墙顶水平位移的影响较大。而G31墙顶水平位移均随着基坑开挖不断减小，且分层厚度和基坑-8.8m～-16.5 m范围内的开挖顺序对G31墙顶水平位移的影响较大。

图11～14分别为1#，3#，5#，8#一柱位置处顶板竖向位移随开挖变化的曲线。观察上述四个图形，首先各水平下1#，3#，5#一柱位置处顶板竖向位移不仅均随着基坑开挖不断隆起沉降，曲线出现波动，而且整个C区的土方开挖顺序对三者位置处的竖向位移都有影响。但分层厚度对三者位置处竖向位移的影响有明显区别，其中对1#一柱位置处顶板竖向位移几乎无影响，对5#一柱位置处顶板竖向位移却有明显影响。其次，各水平下8#一柱位置处顶板竖向位移随基坑开挖的波动较小，开挖顺序对其影响不大，但是分层厚度对它的影响十分明显。

综合上述分析，逆作基坑不仅明显存在开挖参数的规划问题，而且一桩一柱的位置控制了逆作基坑开挖参数对其竖向位移的影响效果。最终根据剖面图4中各个结构的位置，选取地连墙G68，G31墙顶水平位移、G68与1#一柱沉降差异值、4#一柱与5#一柱沉降差异值、G31与8#一柱沉降差异值为输出参数，分别定义为Y1，Y2，Y3，Y4，Y5。统计试验数据得到开挖输出数据如表9所示。

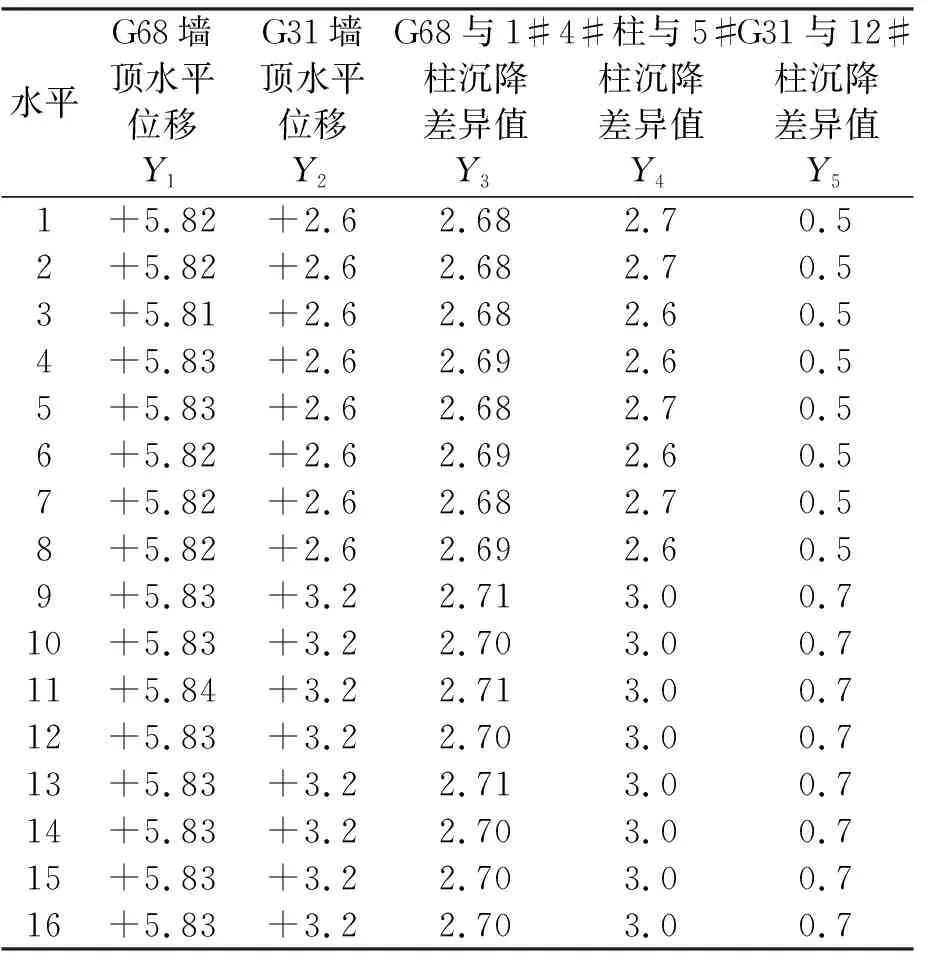
表9 逆作C区基坑开挖输出数据 mm

注：表中墙顶水平位移为“+”代表墙顶向坑内位移；为“-”代表墙顶向坑外位移。表中沉降差异值均为差值的绝对值

3.2.6基于ACE回归逆作开挖响应面

根据确定的输入和输出参数，通过统计学软件包S-Plus中的ACE非参数回归分别得到逆作地下室C区基坑决策变量与各个输出参数间的映射关系。由于篇幅所限，只表示决策变量和地连墙G68墙顶水平位移的映射关系，如表10所示。

表10 C区基坑决策变量与Y1的映射数据

3.2.7基于响应面规划逆作开挖参数

采用枚举法进行逆作C区开挖参数的规划。利用Matlab编程，首先在6个决策变量的取值范围内产生均匀分布的随机数，并通过随机抽样进行计算机仿真模拟，其次重复N次独立随机抽样计算得到大量仿真样本，再次以约束条件对仿真样本进行筛选，最后统计优化目标选出最优值并以此确定出对应的开挖参数。

每次枚举法重复1000次独立随机抽样计算，共进行5次枚举，每次优化结果如表11所示。

表11 逆作C区基坑开挖参数规划结果

以优化目标最优的目的选择工期为11.54 d对应的开挖参数作为规划结果，开挖参数分别为：分层厚度1.68 m；基坑开挖面±0.0～-8.8 m以内土体开挖顺序为岛式开挖，此外所有区域内的土体采用盆式开挖。

4 结 语

本文在建立的优化模型中讨论了逆作法施工下地连墙基坑二维剖面的决策变量及目标函数。并在既有的地连墙支护体系下，研究响应面-枚举法规划逆作开挖的参数使得土方施工工期最短。还通过实例验证了响应面-枚举法规划二维逆作基坑开挖参数的可行性和有效性。

响应面-枚举法不仅适用于小样本空间问题，而且可以解决基坑开挖参数数目多、存在离散性，寻求最优组合维数高等问题。